12
А мое число лучше

Оказывается, создатели «Теории Большого взрыва» решили отметить 73-й эпизод и год рождения актера Джима Парсонса маленькой хвалебной одой числу 73. И почему же это число «лучшее»? Судя по словам Шелдона, потому что:

• 73 – это 21-е простое число;

• зеркальные отражения, или переставленные местами разряды, 73 и 21 – это 37 и 12;

• 37 – это 12-е простое число;

• перемножив цифры 73, можно получить 21;

• а двоичное представление 73 – это 1001001, что является палиндромом (это значит, оно одинаково читается слева направо и справа налево).

Первый и третий факты, безусловно, верны (простым числом является любое натуральное число с ровно двумя натуральными делителями), но вот остальные три – это просто занимательное баловство. Да, 73 – это двухстороннее простое число, но это работает только потому, что мы ведем исчисление в десятичной системе. Это математическое совпадение появилось только потому, что мы использовали пальцы как средство для счета, и, использовав этот краеугольный камень в качестве своего доказательства, Шелдон проявляет антропоцентрический уклон, столь нехарактерный для него. Этот уклон отсутствует в рекламном ролике, снятом примерно в то же самое время, где герои обращаются к зрителям, чтобы обсудить то, что «Теория Большого взрыва», продав права показа, будет теперь транслироваться пять дней в неделю. Шелдон предлагает сделать объявление в пятеричной системе, «системе счисления, которая главенствовала бы, если бы у людей было всего пять пальцев». Это ведет к обсуждению вариантов типа «людей с пятью однопалыми руками».

Что касается его замечания о том, что 73 является палиндромом в своем двоичном варианте, так оно не так уж и примечательно. Поскольку в этой системе используются только два числа – 0 и 1 (см. главу 11), то очень многие числа оказываются палиндромами, включая помощника 73 – число 21 (10101) и его зеркальное отражение 12 (001100), а вот 37 здесь подкачало (100101).

Как отмечает Леонард, спор о том, какое число «лучшее», является неплохим кандидатом в убийцы разговора. С другой стороны, кто-то может сказать, что спор о том, какой дизайнер обуви самый лучший, или какая рок-группа лучше, или сколько пальцев лучше иметь на руке, может быть таким же бесполезным и в соответствующей компании тоже оказаться убийцей разговора.

«Очень трудно работать в команде, если ты всемогущ». Ну да, цитата на самом деле из «Звездного пути: Следующее поколение», но Шелдону она вполне подходит. У него нет какого бы то ни было диагноза, и он не сумасшедший (его мама проверяла), тем не менее откуда такое отношение?  С какой стати он решил, что может навязывать другим мысль, что его число «лучшее»? Слово «наука» означает «знать», и мы знаем, что то, что мы «знаем», – это всего лишь мнение, и оно способно меняться (см. главу 8); разве он этого не «знает»?

Одна из причин, по которой работа в команде чаще всего лучше для решения проблем, чем индивидуальная, в том, что разнообразие идей предлагает больше возможностей для проникновения в суть проблемы. Но Шелдон обычно сторонится сотрудничества, принижает вклад других и увольняет тех, кто осмеливается посягнуть на лавры . За несколькими исключениями, он присоединяется к группам, только чтобы показать свою власть, как в случае с компанией по созданию приложения по узнаванию почерка, или потому, что этого требуют правила, как в случае с командой для Кубка игр по физике .

Лора Шерк Физек, магистр социологии, преподает организационное поведение в Университете Саффолк в Бостоне. Она рассмотрела некоторые аспекты шелдоновского поведения на своих занятиях: его покровительственный тон, его нетерпимость к перебиваниям, его неспособность понимать социальные сигналы, его постоянное ошибочное мнение, что все надеются на него в ситуациях, требующих интеллектуального решения. Затем она анализирует эффекты всех этих черт его характера на примере эпизода «Догадка банки Бэтмена».

Хотя многие зрители считают командирский тон Шелдона главной причиной его дисфункции или разрушения любой группы, к которой он примыкает, Физек не считает это ключевой проблемой. По ее словам, люди не мотивированы оставаться в группе, если их роль не дает им удовлетворения, и при отсутствии общей цели невозможно даже определить подобные роли: «Если вы не делаете того, ради чего вы создали группу, то и группы не существует». В случае с Кубком игр по физике не было ни одной общей задачи, значит, и невозможно говорить о существовании команды. У Леонарда, Говарда и Раджа была одна цель на протяжении всего времени: они хотели выиграть соревнование вместе, всей командой. У Шелдона не было интереса соревноваться, не говоря уже о сотрудничестве, и он соглашается присоединиться к команде только потому, что их нужды превышали его (используя его интерпретацию слов умирающего Спока). Когда его выгоняют из команды, его мотивация меняется, и он хочет отомстить, но, к своему стыду, он оказывается неспособным сделать это самостоятельно. (Интересно, что вопрос, поставивший его в тупик, оказался единственным, который требовал не только знания готовых фактов.)

Не вините Шелдона, предупреждает Физек, он постоянен в своем поведении. Его условие не меняется: он начинает как идивидуум, и он заканчивает в одиночестве. Более того, она аплодирует тому, как он открыто объявляет своих членов команды: «уборщик с третьего этажа, женщина из столовой и, извините мой испанский, то ли ее сын, то ли мясник». В мире Шелдона это его маленькое признание демонстрирует невероятную скромность.

Или же просто напоминание о том, что ему просто наплевать на команды и членов команд.

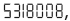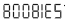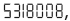Радж позже объясняет, почему он выбрал число 5 318 008 – если написать на калькуляторе  в перевернутом виде оно станет   .

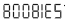(Шелдон здесь упускает возможность контраргумента: 73 в перевернутом виде читается как EL – фамилия Супермена.)

Слова лучше всего прописываются на дешевых калькуляторах с изображением из семи сегментов, где каждая цифра составляется из сплошных линий (такое же изображение часто встречается на спортивных дисплеях со счетом и радиочасах). Если перевернуть такой дисплей вверх ногами, цифры от 0 до 9 становятся похожими на угловатые латинские буквы O, заглавную l (или строчную l), Z, E, h, S, g (или q), L, B, и G или b). Этот несколько ограниченный алфавит может тем не менее быть использован для написания множества слов, многие из которых отражают тонкие чувства и избыток времени юных владельцев этих дешевых калькуляторов. Но, когда некоторые из них взрослеют и становятся астрофизиками или нейробиологами, они перерастают свои семисегментовые дисплеи и приобретают графические калькуляторы гораздо более продвинутого вида. (Крутой графический калькулятор фирмы TI, принадлежащий Майем Биалик, может выделывать изящные извилины и сложные многоуровневые уравнения с замечательным шрифтом, что отвлекает ее от написания всяких шалостей, ну разве что она иногда изобразит на нем ∫ex-y!)

Актриса Джессика Уолтер, которая играет покровительницу науки миссис Лейтам, также играет в комедии «Замедленное развитие», и там на ней надета тюремная форма с номером 0773Ч на груди. И каждый раз, когда она смотрит вниз, ее 5318008 говорят ей h3LL0.

По каким критериям можно вообще измерить «хорошесть» числа? Некоторые числа просто причудливые. У некоторых чисел просто причудливые названия. Примером может послужить группа чисел, известная как «номера такси». В начале ХХ века математик Сриниваса Рамануджан (в его честь был назван один из героев криминальной драмы CBS «4исла») попал в лондонскую больницу. Его хороший друг и математик Готфри Харди («Братья Харди» не были названы в его честь) решил его навестить. После того как они обменялись парочкой шуток типа «извлечение корня из корневого пива в квадратном стакане» и новостями по поводу последних добавлений в ряд Тейлора, Харди упомянул, что он обратил внимание на номер такси, которое привезло его в больницу. (Конечно, обратил. Вы же знаете, что он был математиком?) Это был номер 1729, и ему показалось, что это число было довольно скучным и, возможно, даже не предвещающим ничего хорошего. (Это уж вам решать, могут ли числа быть интересными или приносящими удачу.)

Рамануджан тем не менее не остался спокоен (в конце концов, он тоже был математиком), заметив, что 1729 – это довольно интересное число по той причине, что это наименьшее число, представимое в виде суммы двух кубов двумя способами. Куб – это x³ = x × x × x, если взять пару чисел, назовем их a и b, их сумма в кубе должна удовлетворять равенству a³ + b³ = 1729, при этом 0 < a ≤ b, вторая пара чисел также должна этому соответствовать. (Вы можете найти все эти четыре числа? Если вам неинтересно или у вас нет времени (уверен, у вас бы нашлось время, если бы вы были в больнице и вас навещали только одни математики), в конце главы есть намек.)

Другие числа тоже могут быть представлены в виде суммы двух кубов двумя способами (например, 4104 = 2³ + 16³ = 9³ + 15³), но 1729 оказалось самым маленьким. Это и делает его таким особенным, и именно поэтому оно не оставило Рамануджана равнодушным.

Чтобы запечатлеть это событие в истории и показать, что в душе каждого математика живет поэт, целая группа чисел получила название «номера такси». (Мы могли бы привести здесь точное определение и сказать, что n-й «номер такси» – это наименьшее число, которое может быть представлено суммой двух кубов n-м количеством способов. Но мы признаем, что, когда речь заходит о превращении скучных вещей в интересные, мы Рамануджану и в подметки не годимся.) Самый первый «номер такси» – это 2, поскольку его можно представить суммой двух кубов одним способом (2 = 1³ + 1³). Номер такси Харди, 1729, второй в этом списке. Оно также известно под именем «число Рамануджана—Харди», и, возможно, вы можете догадаться почему. (Математики, конечно, не называют его так все время. Когда маленькие математики играют в прятки, они не считают таким образом: «1727, 1728, Рамануджана—Харди, 1730, я иду искать, кто не спрятался, я не виноват!» Это же ненормально. Но спросите любого математика, что такое «номер такси», и вы тут же услышите эту историю про Рамануджана и Харди и их нескучное такси, хотите ли вы этого или нет.) Надо ли нам восторгаться фактом, что у числа 1729 есть такое свойство? Приносит ли оно хоть какую-то пользу тем, кто не является математиком и не обращает внимания на номера такси? Скорее всего нет (или пока нет, в любом случае), но кто знает, что нас ждет. У многих чисел есть подобные странные свойства, которые оказались полезными в неожиданных ситуациях. Это самое число принесло пользу Рамануджану, который открыл это свойство за много лет до этого происшествия и просто ждал возможности ввернуть его в разговор. (Надеюсь, это не испортило историю для вас?) Однажды кто-нибудь превратит «номера такси» в сложный шифр, или в отличный способ упаковки предметов в твердые контейнеры (может быть, упаковки математиков в такси), или еще во что-нибудь совершенно неожиданное.

В любом случае, это просто пример числа, которое некоторые люди считают лучшим в сравнении со скучным числом 73.

Невзирая на слухи об обратном, Калтех не выдает стипендии за атлетические способности. В этом нет необходимости. Непобежденная (или лучше сказать, не встретившая сопротивления) на поле с 1993 года и до недавнего времени футбольная команда университета славилась рекордом за самое большое количество сыгранных игр на Роуз-Боул (к сожалению, ни одной не было сыграно на Новый год) и выигрышем всухую у всех команд на протяжении целого сезона (это случилось в 1944 году, когда большинство лучших игроков страны были кое-чем заняты). В бейсболе и мужском баскетболе Калтех гордится самым продолжительным периодом пребывания в Национальной ассоциации студенческого спорта (к сожалению, речь не идет о победном периоде).

Отставив в сторону эту сомнительную статистику, призовем факт, что калтеховские атлеты находятся в национальных рекордах по настольному теннису, фехтованию и алтимату. Многие этому удивятся, учитывая злостные стереотипы в обществе относительно сочетания любви к числам и любви к спорту, поскольку 3D-шахматы и собирание кубика Рубика вслепую до сих пор никак не могут пробиться в Олимпийские игры. И тем не менее среди самых заядлых ботаников есть немало фанатов профессионального спорта. Рвение этих ходячих баз данных, выдающих статистику и прогнозы, заставляет шелдоновское детсадовское декламирование «Тысячи и одного знака числа Пи» нервно курить в сторонке .

Калтеховский политолог Род Кивит объединил усилия с бывшим генеральным менеджером лос-анджелесских «Доджеров» Фредом Клэром, чтобы проводить семинар «Теория и практика деньгобола» по aнализу объективной бейсбольной информации. Саберметрика (названная так в честь Исследования общества американского футбола ) – это наука об исследовании статистики игры с целью обнаружения полезной информации. Сейчас почти каждая команда приглашает на работу профессионального саберметриста, и некоторые соотношения, которые были обнаружены, просто невероятны. Оказывается, например, что подсчет среднестатистического отбивания мяча не является показателем побед или поражений.

Так как техника сбора данных продолжает улучшаться, саберметрика теперь находится в своем собственном подразделе экономики. К ней относятся те же законы, ограничения и стратегии, что управляют деньгами.

И я уже молчу о том, что с ее помощью ваша фантазийная бейсбольная команда сможет наконец-то принести вам настоящую прибыль.

«Мне нужно было разобраться в науке, чтобы стать эффективным и авторитетным».

Том Ллойд (выпускник Калтеха 1999 года) сам себя называет «воплощением странных способов карьерного выбора». В первый же свой день в университете, за завтраком, он решил, что больше всего на свете он хочет быть рок-н-рольщиком.

Будучи виолончелистом, он собирался выбрать главными предметами музыку и философию. Вместо этого он стал сооснователем группы, и как только он закончил первый курс, то бросил учебу, чтобы отправиться на гастроли. Со своими козырями – басами Ллойда и вокалом и сумасшедшей прической Дэна Зейнса – Тhe Del Fuegos объехали весь мир за десять лет. Их хитами стали Move With Me Sister («Танцуй со мной, сестренка»), Don’t Run Wild («Не слетай с катушек») и I Still Want You («Ты мне еще нужна») (это три отдельных названия песен, ну или одна очень интересная телеграмма).

Когда остальные члены группы оставили команду, Ллойд, уже будучи 28-летним, решил продолжить свою учебу, но с небольшими корректировками. Он выбрал биоресурсы своей специализацией в Беркли перед тем, как получить докторскую в области экологической инженерии в Калтехе. Затем, когда его интересы снова изменились, он стал консультантом по вопросам управления, затем аналитиком-исследователем, а теперь он вице-президент в международной инвестиционной фирме.

И чтоб вы знали, его докторская была о механизмах, с помощью которых один железосвязывающий компонент, называемый дефероксамин В, растворяет минералы, содержащие оксиды переходных металлов. Где-то здесь затерялась шутка со словом «рок», но, чтобы ее добыть, понадобится доктор наук.