Глава одиннадцатая На что рассчитывать, если вы надеетесь выиграть в лотерею - Как не ошибаться. Сила математического мышления - Джордан Элленберг - RutLib.com

Книга: Как не ошибаться. Сила математического мышления

Дальше: Глава двенадцатая Чаще опаздывайте на самолеты!

Глава одиннадцатая
На что рассчитывать, если вы надеетесь выиграть в лотерею

Следует ли играть в лотерею?

Благоразумным принято считать ответ «нет». Старый афоризм говорит нам, что лотереи – это «налог на глупость», обеспечивающий правительству доход за счет людей, введенных в заблуждение настолько, что они готовы покупать лотерейные билеты. Если воспринимать лотерею как налог, то можно понять, почему лотереи так популярны среди государственных казначейств. Сколько еще налогов люди готовы выплачивать, стоя в очередях у лотерейных терминалов?

Притягательность лотерей – явление далеко не новое. Эта практика началась еще в XVII столетии в Генуе, где лотерея появилась случайно как следствие избирательной системы. Один раз в шесть месяцев в Генуе избирали двух членов Малого совета. Вместо того чтобы проводить выборы, избрание членов совета осуществлялось посредством жеребьевки, когда из кипы бумажек с именами ста двадцати советников вытягивались две полоски. Вскоре городские любители азартных игр стали заключать пари с высокими ставками на результаты избрания членов совета. Эти пари приобрели такую популярность, что игроков начала раздражать вынужденная необходимость ждать дня выборов, чтобы сыграть в эту притягательную азартную игру. Они быстро поняли: чтобы вытягивать полоски бумаги из кучи таких полосок, в выборах вообще нет необходимости. Имена политиков заменили числами, и в 1700 году в Генуе уже действовала лотерея, которая показалась бы очень знакомой тем, кто играет в современную американскую лотерею Powerball. Игроки пытались угадать пять случайно выпавших номеров, причем чем больше чисел игрок угадывал, тем больше был его выигрыш.

Лотереи быстро распространились по всей Европе, а оттуда попали в Северную Америку. Во время Войны за независимость как континентальный Конгресс, так и правительства штатов организовывали лотереи для финансирования борьбы с британцами. В Гарварде в 1794 и 1810 годах (во времена, когда фонд финансирования университета еще не исчислялся в девятизначных цифрах) были проведены лотереи для сбора средств на строительство двух новых университетских зданий. (Эти здания до сих пор используются в качестве общежитий для первокурсников.)

Не все приветствовали это новшество. Моралисты не без оснований считали, что лотереи равносильны азартным играм. Противником лотерей был также и Адам Смит. В своем труде The Wealth of Nations («Исследование о природе и причинах богатства народов») он писал:

О том, что шансы удачи естественно переоцениваются, мы можем судить по всеобщему успеху лотерей. На свете никогда не было и не будет вполне справедливой и честной лотереи, то есть такой, в которой все выигрыши уравновешивали бы все потери, ибо в таком случае устроитель ее не имел бы никакой выгоды. В государственных лотереях билеты в действительности не стоят той цены, какую уплачивают за них первоначальные подписчики, а между тем они обычно продаются на рынке с надбавкой в 20, 30 и иногда 49 %… В лотерее, в которой ни один выигрыш не превышал бы 20 ф., спрос на билеты был бы меньше, хотя бы эта лотерея в других отношениях была гораздо справедливее и честнее, чем обычные государственные лотереи. Чтобы заручиться большими шансами на получение одного из крупных выигрышей, некоторые люди покупают по нескольку билетов, а другие – мелкие доли еще большего количества их. Однако одно из наиболее достоверных математических положений состоит в том, что чем больше билетов вы рискуете приобрести, тем скорее вы окажетесь в проигрыше. Рискните на все билеты лотереи, и вы наверняка проиграете, и чем больше число ваших билетов, тем несомненнее ваш проигрыш.

Убедительность высказываний Смита и его достойное восхищения упорство в рассмотрении количественных показателей не должны скрыть от вас тот факт, что его вывод, строго говоря, неверен. Большинство игроков в лотерею сказали бы, что покупка двух лотерейных билетов вместо одного не увеличивает вероятность проигрыша, а в два раза повышает вероятность выигрыша. И были бы правы! В лотерее с простой призовой структурой легко проверить все самостоятельно. Предположим, в лотерее 10 миллионов комбинаций чисел и только один победитель. Стоимость билетов 1 доллар, а приз – 6 миллионов долларов.

Человек, купивший все билеты до единого, потратит 10 миллионов долларов и получит приз в размере 6 миллионов долларов. Другими словами, как и говорил Смит, это явно проигрышная стратегия, которая обойдется игроку в 4 миллиона долларов. Мелкий игрок, купивший всего один билет, находится в более выгодном положении: у него есть как минимум один шанс из 10 миллионов остаться с прибылью!

Но, что если вы купите два билета? В таком случае вероятность проигрыша сокращается, хотя, надо признать, всего с 9 999 999 из 10 миллионов до 9 999 998 из 10 миллионов. Чем больше билетов вы покупаете, тем больше снижается вероятность проигрыша, но только пока вы не купите 6 миллионов билетов. В этом случае вероятность выиграть приз, а значит, остаться при своих, составляет целых 60 %, тогда как вероятность проиграть равна всего 40 %. Вопреки утверждению Смита, покупка большего количества лотерейных билетов позволит вам снизить вероятность проигрыша.

Но если вы купите хотя бы еще один билет, потеря денег неизбежна (хотя о какой именно сумме идет речь, 1 доллар или 4 000 001 доллар, зависит от того, есть ли среди ваших билетов выигрышный).

Здесь трудно воссоздать ход рассуждений Смита, но вполне возможно, что он стал жертвой заблуждения «все линии являются прямыми», сделав вывод о том, что если покупка всех лотерейных билетов непременно приведет к потере денег, то и покупка большего количества билетов также приведет к повышению вероятности потери денег. Человек, купивший один билет, почти полностью уверен, что потеряет деньги, но знает, что не потеряет много денег. Тот, кто купил 6 миллионов билетов, находится в гораздо более опасном положении. Скорее всего, вам все еще кажется, что оба эти решения не очень разумны. Как говорил Смит, если лотерея – это выигрышное дело для государства, значит, для каждого, кто находится по другую сторону сделки, это наверняка не лучший вариант.

В аргументах Смита против лотерей отсутствует понятие ожидаемой ценности – математический формализм, отображающий ту интуитивную догадку, которую он сам и пытался сформулировать. Вот в чем суть этой концепции. Предположим, у нас есть предмет, имеющий неопределенную денежную стоимость, скажем лотерейный билет:

в 9 999 999 из 10 000 000 случаев билет ничего не стоит;

в 1 из 10 000 000 случаев билет стоит 6 миллионов долларов.

Несмотря на эту неопределенность, нам все же может понадобиться присвоить лотерейному билету определенную ценность. Зачем? Что если какой-то человек предлагает людям заплатить по 1,2 доллара за их билеты? Целесообразно ли пойти на эту сделку и положить в карман 20 центов или лучше придержать билет? Это зависит от того, какую ценность вы присвоили этому билету – больше или меньше 1,2 доллара.

Вот как можно вычислить ожидаемую ценность лотерейного билета. Для каждого возможного результата необходимо умножить вероятность результата на ценность билета в случае получения этого результата. В нашем упрощенном примере существует только два варианта: проигрыш или выигрыш. Следовательно, вы получите такие числа:

9 999 999/10 000 000 × 0 долларов = 0;

1/10 000 000 × 6 000 000 долларов = 0,60 доллара.

Затем необходимо сложить эти числа:

0 долларов + 0,60 доллара = 0,60 доллара.

Таким образом, ожидаемая ценность вашего лотерейного билета составляет 60 центов. Если какой-то фанат лотерей постучит в вашу дверь и предложит 1,2 доллара за ваш билет, ожидаемая ценность этого билета говорит о том, что вам следует пойти на эту сделку. В действительности ожидаемая ценность билета говорит, что вы вообще не должны были платить за него один доллар!

Ожидаемая ценность – вовсе не та ценность, которую вы ожидаете

Ожидаемая ценность – еще одна математическая концепция, имеющая (подобно значимости) название, которое не совсем верно отражает ее значение. Разумеется, мы не «ожидаем», чтобы лотерейный билет стоил 60 центов; напротив, он стоит либо 10 миллионов долларов, либо ничего, и никаких промежуточных значений.

То же самое происходит и в следующей ситуации. Предположим, я делаю ставку 10 долларов на собаку, которая, по моему мнению, с вероятностью 10 % выиграет собачьи бега. Если собака победит, я получу 100 долларов; если собака проиграет, я не получу ничего. В таком случае ожидаемая ценность этого пари составляет:

(10 % × 100 долларов) + (90 % × 0 долларов) = 10 долларов.

Но я ожидаю совсем не этого. Выигрыш 10 долларов – по сути, даже не один из возможных результатов моего пари, не говоря уже об ожидаемом. Лучше было бы назвать это «средняя ценность», поскольку на самом деле ожидаемая ценность пари представляет собой количественную оценку того, какого результата я мог бы ожидать, если сделал бы много таких ставок на большое количество собак. Предположим, я заключил тысячу таких пари со ставкой 10 долларов. По всей вероятности, я выиграл бы сотню пари (снова закон больших чисел!) и заработал бы по 100 долларов на каждом из них, то есть всего 10 000 долларов. Следовательно, тысяча ставок принесет мне прибыль в среднем по 10 долларов на одну ставку. В долгосрочной перспективе можно даже остаться при своих.

Ожидаемая ценность – это отличный способ определить справедливую цену объекта (такого как ставка на собачьих бегах), истинная ценность которого неизвестна. Если я заплачу за каждый билет на бега по 12 долларов, в долгосрочной перспективе я с большой вероятностью потеряю деньги; если мне удастся найти такие билеты по 8 долларов, тогда мне следует купить их как можно больше. Сейчас почти никто не делает ставки на собачьих бегах, но механизм ожидаемой ценности один и тот же, что бы вы ни пытались оценить: билеты на бега, фондовые опционы, лотерейные билеты или страхование жизни.

Закон о миллионе

Понятие ожидаемой ценности привлекло внимание математиков еще в середине XVII столетия, а к концу столетия эта идея была уже настолько изученной, что ее использовал даже такой ученый-практик, как Эдмунд Галлей, Королевский астроном Англии. Да, человек, который занимался кометами! Но он был также одним из первых ученых, изучавших вопрос правильного ценообразования страховых продуктов, что в период правления Вильгельма III было делом чрезвычайной важности. Англия с энтузиазмом вступила в войну на континенте, а война требовала денег. Парламент предложил добыть необходимые средства посредством принятого в 1692 году «Закона о миллионе», призванного собрать миллион фунтов за счет продажи пожизненных аннуитетов населению. Чтобы получить такой аннуитет, необходимо было заплатить короне изрядную сумму в обмен на гарантированные пожизненные ежегодные выплаты. Это своего рода страхование жизни наоборот: по существу, покупатели аннуитета делали ставку на то, что они в скором времени не умрут. Актуарная наука находилась в то время в зачаточном состоянии, поэтому стоимость аннуитета устанавливалась без учета возраста получателя аннуитета! Пожизненный аннуитет для дедушки, который мог получать ежегодные выплаты самое большее на протяжении десяти лет, имел такую же стоимость, что и аннуитет для ребенка.

Галлей был довольно грамотным ученым, чтобы понимать всю абсурдность схемы ценообразования, не зависящей от возраста. Он решил разработать более рациональный метод расчета стоимости пожизненного аннуитета. Проблема была в том, что люди не приходят в этот мир и не покидают его по такому же строгому графику, как это делают кометы. Однако, воспользовавшись статистическими данными рождаемости и смертности, он смог оценить вероятную продолжительность жизни каждого получателя аннуитета, а значит, и рассчитать ожидаемую ценность аннуитета: «Очевидно, что покупатель должен заплатить только за ту часть стоимости аннуитета, которая соответствует вероятной продолжительности его жизни; эту стоимость следует рассчитывать по годам, а сумма всех этих годовых значений даст стоимость аннуитета в расчете на продолжительность жизни рассматриваемого человека».

Другими словами, дедушка с его более короткой ожидаемой продолжительностью жизни платит за аннуитет меньше, чем его внук.

Ремарка в сторону: «Ето есть очевидно»

Когда я рассказываю людям историю об Эдмунде Галлее и о цене аннуитетов, меня часто прерывают словами: «Но это же очевидно, что молодым следует назначать более высокую цену!»

Нет, совсем не очевидно. Пожалуй, это действительно кажется очевидным, если вы, будучи современными людьми, уже кое о чем знаете. Сам факт, что люди, занимавшиеся аннуитетами, каждый раз упускали это из виду, – уже служит доказательством того, что на самом деле все не так очевидно. В математике есть множество идей, который сейчас кажутся очевидными (например, что отрицательные величины можно складывать и вычитать, что точку на плоскости полезно представлять в виде пары чисел, что вероятность неопределенных событий можно описать математически и манипулировать соответствующими значениями), однако в действительности они далеко не очевидны. Если все было бы так, все подобные идеи возникли бы не на столь позднем этапе развития человеческой мысли.

Наша тема напомнила мне старый случай, связанный с одним замечательным российским профессором, которого мы назывем профессором О, – эту историю любят рассказывать на математическом факультете Гарвардского университета. Профессор О дошел уже до середины вывода сложной алгебраической формулы, когда студент из заднего ряда поднял руку.

– Профессор, я не понял последнего шага. Почему эти два оператора коммутируют?

– Но ето есть очевидно, – слегка удивленно ответил профессор О.

– Простите, профессор, но я на самом деле этого не вижу, – продолжал упорствовать студент.

Профессор О вернулся к доске и написал на ней еще несколько строк объяснения.

– Что мы должны сделать? Так вот, два оператора приведены к диагональному виду… ну, не совсем диагональному, но… минуточку…

Профессор О помолчал еще немного, уставившись на то, что было на доске, и почесывая подбородок. Затем он ушел в свой кабинет. Прошло около десяти минут. Студенты уже собирались уходить, когда профессор О вернулся и снова занял свое место у доски.

– Да, – удовлетворенно произнес он. – Да, ето есть очевидно.

Не играйте в Powerball

В настоящее время американская государственная лотерея Powerball разыгрывается в сорока двух штатах, в округе Колумбия и на Виргинских островах США. Это невероятно популярная лотерея: иногда продается целых 100 миллионов билетов на один розыгрыш. В Powerball играют бедные люди, в Powerball играют те, кто уже разбогател. В Powerball играет мой отец, бывший президент Американской статистической ассоциации, а поскольку он покупает билеты и для меня, значит, и я тоже играю.

Разумно ли это?

Шестого декабря 2013 года, когда я пишу эти строки, джекпот составляет довольно большую сумму, 100 миллионов долларов. И джекпот – это не единственный способ выиграть. Подобно многим другим лотереям, в Powerball действует многоуровневая система призов; более мелкие и чаще встречающиеся призы позволяют поддерживать у людей ощущение того, что в эту лотерею стоит играть.

С помощью ожидаемой ценности мы в состоянии сопоставить эти ощущения с математическими фактами. Вот как можно рассчитать ожидаемую ценность лотерейного билета за 2 доллара. Покупая билет, вы приобретаете следующее:

1 шанс из 175 000 000 выиграть джекпот 100 миллионов долларов;

1 шанс из 5 000 000 выиграть приз 1 миллион долларов;

1 шанс из 650 000 выиграть приз 10 тысяч долларов;

1 шанс из 19 000 выиграть приз 100 долларов;

1 шанс из 12 000 выиграть другой приз 100 долларов;

1 шанс из 700 выиграть приз 7 долларов;

1 шанс из 360 выиграть другой приз 7 долларов;

1 шанс из 110 выиграть приз 4 доллара;

1 шанс из 55 выиграть другой приз 4 доллара.

(Все эти данные можно получить на сайте Powerball, на котором есть также на удивление остроумная страница «Часто задаваемые вопросы», где можно найти нечто в таком роде: «Вопрос: заканчивается ли срок действия билетов Powerball? Ответ: да; Вселенная затухает, и ничто не вечно».)

Таким образом, ожидаемая сумма, которую вы можете выиграть, равна:

100 миллионов / 175 миллионов + 1 миллион / 5 миллионов + 10 000 / 650 000 + 100 / 19 000 + 100 / 12 000 + 7 / 700 + 7 / 360 + 4 / 110 + 4 / 55,

что составляет немногим менее 94 центов. Другими словами, с точки зрения ожидаемой ценности лотерейный билет не стоит ваших двух долларов.

Но это не конец истории, поскольку не все лотерейные билеты одинаковые. Когда джекпот составляет 100 миллионов долларов (как сегодня), ожидаемая ценность билета возмутительно низка. Но каждый раз, когда джекпот остается невостребованным, в призовой фонд поступает дополнительная сумма денег. Чем больше становится джекпот, тем больше людей покупают лотерейные билеты и тем больше вероятность того, что один из этих билетов сделает кого-то мультимиллионером. В августе 2012 года работник железной дороги из штата Мичиган Дональд Лоусон сорвал джекпот в размере 337 миллионов долларов.

Когда главный приз становится настолько большим, ожидаемая ценность билета также увеличивается. Для того чтобы рассчитать эту ценность, достаточно подставить в приведенную выше формулу сумму 337 миллионов:

337 миллионов / 175 миллионов + 1 миллион / 5 миллионов + 10 000 / 650 000 + 100 / 19 000 + 100 / 12 000 + 7 / 700 + 7 / 360 + 4 / 110 + 4 / 55,

что составляет 2,29 доллара. Отныне игра в лотерею уже не кажется таким безнадежным делом. Насколько большим должен быть джекпот, чтобы ожидаемая ценность лотерейного билета превысила его цену в два доллара? Теперь вы можете вернуться к учительнице, которая преподавала вам математику в восьмом классе, и сказать ей, что вы поняли, зачем нужна алгебра. Если мы обозначим величину джекпота буквой J, ожидаемая ценность билета равна:

J / 175 миллионов + 1 миллион / 5 миллионов + 10 000 / 650 000 + 100 / 19 000 + 100 / 12 000 + 7 / 700 + 7 / 360 + 4 / 110 + 4 / 55,

или, если упростить эту формулу:

J / 175 миллионов + 36,7 цента.

В этот момент в игру вступает алгебра. Чтобы ожидаемая ценность лотерейного билета оказалась больше двух долларов, которые вы на него потратили, необходимо, чтобы значение J / 175 миллионов было больше 1,63 доллара или что-то около этого. Умножив обе стороны на 175 миллионов, вы обнаружите, что пороговая величина джекпота составляет немногим более 285 миллионов долларов. Это не такое уж редкое событие: в 2012 году такой джекпот был три раза. Создается впечатление, что по большому счету игра в лотерею может быть неплохой идеей – если вы достаточно осмотрительны, чтобы играть только тогда, когда джекпот становится достаточно большим.

Но и это еще не конец истории. Вы не единственный человек в Америке, знакомый с алгеброй. И даже люди, не знающие алгебры, инстинктивно понимают, что лотерейный билет более заманчив, когда джекпот составляет 300 миллионов долларов, а не 80 миллионов. Как и всегда, математический подход – формализованная версия наших природных мысленных расчетов, продолжение здравого смысла другими средствами. В случае типичного розыгрыша с джекпотом 80 миллионов долларов может быть продано около 13 миллионов билетов. Но когда Дональд Лоусон выиграл 337 миллионов долларов, вместе с ним в лотерею играли еще около 75 миллионов человек.

Чем больше людей играет, тем больше людей выигрывают призы. Но джекпот только один. И если два человека угадали все шесть чисел, они должны разделить эти большие деньги.

Какова вероятность того, что вы выиграете джекпот и вам не придется им делиться? Для этого должны произойти две вещи. Прежде всего вы должны угадать все шесть чисел; вероятность сделать это составляет один шанс из 175 миллионов. Но недостаточно просто выиграть: все остальные должны проиграть.

Существует неплохая вероятность, что любой отдельно взятый игрок упустит джекпот – около 174 999 999 из 175 миллионов. Но если в игре принимает участие 75 миллионов игроков, существует довольно большая вероятность, что один из них сорвет джекпот.

Насколько велика эта вероятность? Чтобы определить это, давайте используем факт, с которым встречались уже не раз: если мы знаем вероятность одного события и знаем вероятность другого события и если эти два события независимы (наступление одного события не влияет на наступление другого), тогда вероятность наступления первого и второго событий равна произведению вероятностей наступления этих двух событий.

Слишком абстрактные рассуждения? Тогда рассмотрим их на примере лотереи.

Вероятность того, что я проиграю, составляет 174 999 999 из 175 000 000, а вероятность того, что мой отец проиграет, – 174 999 999 из 175 000 000. Следовательно, вероятность того, что мы оба проиграем, равна:

174 999 999 / 175 000 000 × 174 999 999 / 175 000 000,

или 99,9999994 %. Другими словами, как я и говорю своему отцу каждый раз, нам лучше не бросать работу.

Но какова вероятность того, что проиграют все 75 миллионов ваших соперников? Все, что мне нужно сделать, – это умножить 174 999 999 / 175 000 000 на себя 75 миллионов раз. Похоже на наказание за совершение особо тяжкого преступления. Но данную задачу можно существенно упростить, представив ее в виде степени, которую ваш компьютер вычислит мгновенно:

(174 999 999 / 175 000 000)75 миллионов = 0,651…

Следовательно, существует вероятность 65 %, что ни один из ваших товарищей по игре не выиграет, а это значит, что один из них все-таки может выиграть с вероятностью 35 %. Если это действительно произойдет, ваша доля от приза в размере 337 миллионов долларов составит ничтожных 168 миллионов. Что сокращает ожидаемую ценность джекпота до

65 % × 337 миллионов долларов + 35 % × 168 миллионов долларов = 278 миллионов долларов.

Это немного ниже пороговой величины джекпота в размере 285 миллионов долларов, которая делает джекпот стоящим того, чтобы играть в лотерею. А ведь во всех наших расчетах не учитывалась вероятность того, что джекпот сорвут более чем два игрока, когда большой приз пришлось бы разделить на еще большее количество частей. Возможность разбиения джекпота на части означает, что ожидаемая ценность лотерейного билета меньше, чем сумма, которую вы на него потратили, даже когда джекпот достигает 300 миллионов долларов. Если джекпот стал бы еще больше, ожидаемая ценность могла бы попасть в зону «оно того стоит» – или нет, если большой джекпот повлек бы за собой еще более высокий уровень продаж билетов. Самый крупный джекпот в лотерее Powerball, составивший 558 миллионов долларов, выиграли два игрока, а самым большим джекпотом за всю историю США стал главный приз в размере 668 миллионов долларов в лотерее Mega Millions, который был разделен на три части.

А ведь мы еще не говорили ни о налогах, которые вы должны будете выплатить со своего выигрыша, ни о том, что выигрыш будет выплачиваться вам частями по определенной сумме в год, а если вы хотите получить всю сумму сразу, вам выплатят существенно меньше денег. И помните: лотерею организует государство, а государство многое о вас знает. Во многих штатах невыплаченные налоги или другие непогашенные финансовые обязательства оплачиваются из выигрыша по лотерее, прежде чем вы увидите хотя бы цент. Один мой знакомый, работающий в государственной лотерее, рассказал мне историю о человеке, который пришел в офис лотереи с подругой, чтобы получить деньги на свой выигрышный билет в размере 10 000 долларов и провести бурный уик-энд, предаваясь всевозможным городским удовольствиям. Когда он предъявил выигрышный билет, официальный представитель лотереи сообщил паре, что почти все призовые деньги, кроме нескольких сотен долларов, уже переведены для погашения невыплаченных алиментов на ребенка, которые этот человек был должен своей бывшей подруге.

Спутница того человека впервые услышала, что у него есть ребенок. Выходные прошли совсем не так, как планировалось.

Так какой же должна быть лучшая стратегия того, как можно разбогатеть, играя в лотерею Powerball? Вот мой математически обоснованный план, состоящий из трех пунктов.

1. Не играйте в Powerball.

2. Если вы все-таки играете в Powerball, не делайте этого до тех пор, пока джекпот не станет по-настоящему большим.

3. Если вы покупаете лотерейные билеты в надежде выиграть большой джекпот, попытайтесь сократить вероятность того, что вам придется разделить свою добычу с другими победителями: выбирайте числа, которых другие игроки не выберут. Не выбирайте дату своего рождения. Не выбирайте числа, выпавшие в предыдущем розыгрыше. Не выбирайте числа, которые образуют красивый узор в билете. И ради бога, не выбирайте числа, которые вы находите в печенье с предсказаниями. (Надеюсь, вы знаете, что производители не вкладывают в каждое печенье бумажки с разными числами?)

Powerball – не единственная лотерея, но у всех лотерей есть одна общая черта: это плохое пари. Лотерея, как отметил Адам Смит, предназначена для того, чтобы вернуть государству определенную долю от продажи лотерейных билетов; чтобы такое было возможно, государство должно выручить за продажу билетов больше денег, чем оно выделяет на выплату призов. Если взглянуть на это с другой стороны, игроки в лотерею в среднем тратят больше денег, чем выигрывают. Следовательно, ожидаемая ценность лотерейного билета должна быть отрицательной.

За исключением случаев, когда она такой не является.

Лотерейная афера, которая таковой не была

Двенадцатого июля 2005 года в отдел по соблюдению правил проведения лотереи штата Массачусетс поступил необычный звонок от сотрудника супермаркета сети Star Market, что в Кембридже – городе, расположенном к северу от Бостона. Кембридж славится своими учебными заведениями: Гарвардом и Массачусетским технологическим институтом (Massachusetts Institute of Technology; далее по тексту – MIT). Дело заключалось в том, что в супермаркет зашел студент университета, чтобы купить билеты новой лотереи штата Cash WinFall. В этом не было бы ничего необычного, если бы не размер заказа: студент предъявил четырнадцать тысяч игровых карточек, заполненных вручную (каждая!), на общую сумму 28 000 долларов.

Никаких проблем, сказали в офисе лотереи сотруднику супермаркета: если карточки заполнены должным образом, любой человек может покупать столько билетов, сколько пожелает. Если магазины хотели продавать билетов больше чем на 5000 долларов в день, им необходимо было получить в офисе лотереи официальное разрешение, но такие разрешения предоставлялись без всяких проблем.

Все складывалось хорошо, поскольку Star Market не был единственным магазином в районе Бостона, продающим билеты этой лотереи, у которого на той неделе лотерейный бизнес шел весьма активно. Накануне розыгрыша 14 июля еще двенадцать магазинов связались с офисом лотереи с просьбой о предоставлении официального разрешения. Три из них были расположены в Куинси – городке к югу от Бостона на берегу Бостонского залива, в котором обитает много американцев азиатского происхождения. Десятки тысяч лотерейных билетов Cash WinFall были проданы небольшой группе покупателей в нескольких магазинах.

Что же происходило? Ответ на этот вопрос не был секретом; он лежал у всех на виду – в правилах проведения лотереи Cash WinFall. Новая лотерея, запущенная осенью 2004 года, заняла место прежней лотереи Mass Millions, которая была закрыта, после того как на протяжении целого года никто не выиграл джекпот. Игроки все больше разочаровывались в ней, в связи с чем объем продаж лотерейных билетов сократился. Штату Массачусетс необходимо было кардинальным образом реорганизовать свою лотерею, и у руководства штата возникла идея использовать адаптированную версию лотереи штата Мичиган WinFall. В лотерее Cash WinFall джекпот не становился все больше и больше с каждой неделей, на протяжении которой джекпот никто не выигрывал. Вместо этого каждый раз, когда джекпот превышал 2 миллиона долларов, эти деньги передавались на увеличение размера призов других категорий, выиграть которые было не слишком трудно. При этом на следующий розыгрыш устанавливалась минимальная сумма джекпота в размере 500 000 долларов. Комиссия по проведению лотереи рассчитывала на то, что новая лотерея, позволяющая получить серьезный выигрыш, не сорвав джекпота, покажется игрокам выгодным делом.

Организаторы лотереи штата Массачусетс сделали свою работу слишком хорошо. Получилось так, что они создали лотерею Cash WinFall, которая действительно была выгодной. Летом 2005 года несколько предприимчивых игроков поняли это.

Вот каким было распределение призов лотереи Cash WinFall в обычный день.

Если сумма джекпота составляет один миллион долларов, ожидаемая ценность двухдолларового билета достаточно низкая:

(1 миллион долларов / 9,3 миллиона) + (4000 долларов / 39 000) + (150 долларов / 800) + (5 долларов / 47) + (2 доллара / 6,8) = 79,8 цента.

Такая доходность выглядит настолько мизерной, что на этом фоне участники лотереи Powerball выглядят весьма проницательными инвесторами. (И мы еще щедро оценили бесплатный билет в 2 доллара, в которые он обошелся бы вам вместо существенно меньшей ожидаемой ценности.)

Однако в день перераспределения суммы джекпота, превышающей 2 миллиона долларов, ситуация выглядит совсем иначе. Седьмого февраля 2005 года джекпот вырос почти до 3 миллионов долларов. Этот джекпот не выиграл никто, что не удивительно, учитывая то, что в тот день в лотерею Cash WinFall играли всего 470 тысяч человек, а вероятность совпадения всех шести номеров составляла 1 из 10 миллионов.

В итоге эти деньги были переданы в фонд других призовых категорий. Согласно формуле, установленной властями штата, 600 тысяч долларов было перенесено в фонд призовых категорий «Пять совпадений» и «Три совпадения» и 1,4 миллиона долларов – в фонд категории «Четыре совпадения». Вероятность угадать в лотерее WinFall четыре номера из шести составляет 1 из 800, а значит, в тот день должно было быть около шестисот победителей в категории «Четыре совпадения» из 470 тысяч игроков. Это большое количество победителей, но 1,4 миллиона долларов – тоже большие деньги. Если разделить данную сумму среди шестисот победителей в данной категории, получится более 2000 долларов на каждого из них. На самом деле в тот день игроки, угадавшие четыре числа, могли рассчитывать на выигрыш в размере 2385 долларов. Это гораздо более выгодно, чем ничтожные 150 долларов, которые можно было получить в обычный день. В случае получения выигрыша в размере 2385 долларов с вероятностью 1 из 800 ожидаемая ценность лотерейного билета составляет:

2364 доллара / 800 = 2,98 доллара.

Другими словами, один только приз за угадывание четырех чисел делает лотерейный билет заслуживающим его цены в размере 2 доллара. Если учесть другие призовые категории, ситуация становится еще более привлекательной.

Следовательно, лотерейный билет предположительно мог обеспечить средний выигрыш в размере:

50 000 долларов / 39 000 + 2385 долларов / 800 + 60 долларов / 47 = 5,53 доллара.

Инвестиция, которая может обеспечить вам три с половиной доллара прибыли на 2 вложенных доллара, – это не тот шанс, от которого отказываются.

Безусловно, если в такой день один счастливчик сорвет джекпот, для всех остальных игра превратится в тыкву. Однако лотерея Cash WinFall никогда не была настолько популярной, чтобы это могло произойти. За всю историю Cash WinFall сумма джекпота, превышающая определенный уровень, переносилась в фонд других призовых категорий 45 раз, и только однажды игрок угадал все шесть чисел, и процесс перераспределения суммы был остановлен.

Давайте внесем ясность: эти расчеты не означают, что ставка в 2 доллара обязательно позволит вам выиграть деньги. Напротив, когда вы покупаете билет Cash WinFall в день передачи суммы джекпота в фонд других призовых категорий, ваш билет, скорее всего, окажется проигрышным, как и в любой другой день. Ожидаемая ценность – это не та ценность, которую вы ожидаете! Однако в день перераспределения призового фонда призы (в случае маловероятного события, когда вы все же выиграете) становятся больше – намного больше. Магия ожидаемой ценности состоит в том, что средний выигрыш в случае сотни, или тысячи, или десяти тысяч билетов с большой вероятностью составит около 5,53 доллара. Возможно, любой отдельно взятый билет ничего не стоит, но, если у вас тысяча билетов, можете быть уверены в том, что вы вернете вложенные деньги и даже немного заработаете.

Но кто покупает тысячу билетов за один раз?

Студенты MIT – вот кто.

Я могу рассказать вам обо всех (до последнего доллара) выигрышах в лотерею WinFall 7 февраля 2005 года только потому, что эти данные содержатся в исчерпывающем и, честно говоря, захватывающем отчете по делу WinFall, который в июле 2012 года подал властям штата Массачусетс генеральный инспектор штата Грегори Салливан. Думаю, у меня есть все основания утверждать, что это единственный документ о фискальном надзоре за всю историю нашего государства, который заставляет задуматься: а кому принадлежат права на экранизацию всего этого?

Причина, почему в отчете отображены данные именно за этот день, состоит в следующем. Седьмого февраля 2005 года состоялось первое перераспределение призового фонда, после того как студент последнего курса MIT Джеймс Харви, который работал в то время над самостоятельным исследовательским проектом по сравнению преимуществ различных государственных лотерей, понял, что власти штата Массачусетс случайно создали невероятно прибыльный инвестиционный инструмент для любого человека, достаточно хорошо разбирающегося в числах, чтобы обратить на это внимание. Харви собрал группу друзей (в MIT совсем не трудно найти друзей, которые способны рассчитать математическое ожидание) и купил тысячу лотерейных билетов. Как и следовало ожидать, один из билетов оказался выигрышным в категории «Четыре совпадения», и группа получила один приз в размере 2000 долларов. Кроме того, группа получила несколько выигрышей в категории «Три совпадения». В итоге общая сумма выигрыша группы оказалась в три раза больше первоначально вложенной суммы.

Вряд ли я удивлю вас, если скажу, что Харви и другие инвесторы из его группы не прекратили играть в лотерею Cash WinFall. Или что он так и не закончил то самостоятельное исследование – во всяком случае, не довел его до того уровня, чтобы получить свой зачет на экзамене. На самом деле исследовательский проект Харви быстро перерос в преуспевающий бизнес. Летом того года сообщники Харви покупали десятки тысяч лотерейных билетов на один розыгрыш: именно один из членов его группы купил такое огромное количество лотерейных билетов в супермаркете Star Market в Кембридже. Студенты назвали свою команду Random Strategies («Случайные стратегии»), хотя их подход представлял собой не более чем беспорядочный перебор вариантов. Скорее всего, это название произошло от Random Hall, общежития MIT, в котором Харви придумал свой план обогащения за счет лотереи WinFall.

И этим занимались не только студенты MIT. Были созданы как минимум еще две группы, которые пытались воспользоваться преимуществами «денежного водопада» лотереи WinFall. Инь Чжан, врач-исследователь из Бостона с дипломом PhD Северо-Восточного университета, организовал Doctor Zhang Lottery Club. Именно действия DZLC стали причиной всплеска продаж лотерейных билетов в Куинси. Вскоре группа покупала лотерейные билеты на сумму 300 тысяч долларов при каждом перераспределении призового фонда. В итоге доктор Чжан в 2006 году отказался от врачебной практики, полностью посвятив себя лотерее Cash WinFall.

Еще одну группу такого рода возглавлял Джеральд Селби, пенсионер семидесяти с лишним лет, имеющий диплом бакалавра по математике. Селби жил в Мичигане, на родине лотереи WinFall, а его группа состояла из тридцати двух игроков, в основном родственников, которые играли в WinFall на протяжении двух лет, пока в 2005 году лотерея не была упразднена. Когда Селби узнал, что его кормушка возобновилась на востоке, он предпринял очевидный шаг: в августе 2005 года они с женой Марджори отправились в Дирфилд, расположенный в западной части штата Массачусетс, и сделали свою первую ставку – 60 тысяч долларов. Домой они увезли немногим более 50 тысяч долларов чистой прибыли. Селби с его опытом игры в лотерею в штате Мичиган прибавил к своим билетам лотереи Cash WinFall еще один способ получить дополнительную прибыль. В штате Массачусетс магазины получали 5 % комиссионных от продажи лотерейных билетов. Селби заключил прямую сделку с одним магазином, предложив покупать лотерейные билеты на сотни тысяч долларов за один раз в обмен на разделение 5 % комиссионных поровну. Один только этот шаг обеспечил команде Селби дополнительную прибыль в тысячах долларов на каждый розыгрыш с перераспределением призового фонда.

Вам не нужен диплом MIT, чтобы понять, как наплыв крупных игроков повлиял на игру. Не забывайте: выигрыши в день перераспределения призового фонда возросли, потому что большую сумму денег разделяли среди нескольких победителей. В 2007 году на каждый розыгрыш с перераспределением призового фонда продавалось не менее миллиона лотерейных билетов, большинство из которых покупали три крупные группы игроков. Те времена, когда можно было получить приз 2300 долларов за угадывание четырех чисел из шести, канули в лету: если билеты покупали полтора миллиона игроков и один из каждых восьми сотен угадывал четыре числа, тогда победителей в категории «Четыре совпадения» было около двух тысяч. Таким образом, доля каждого из них в общем призовом фонде этой категории в размере 1,4 миллиона долларов теперь сократилась примерно до 800 долларов.

Определить размер выигрыша крупного игрока в лотерее Cash WinFall не составит труда – все дело в том, чтобы проанализировать это с точки зрения самой лотереи. В день розыгрыша с перераспределением призового фонда в распоряжении штата есть (минимум!) 2 миллиона долларов накопленного джекпота, от которых штат должен избавиться. Предположим, в этот день полтора миллиона человек купят лотерейные билеты. Это еще 3 миллиона долларов дохода, из которых 40 %, или 1,2 миллиона долларов, уходит в казну штата, а оставшиеся 1,8 миллиона долларов вносятся в фонд джекпота, причем все эти деньги должны быть выплачены игрокам до окончания дня. Следовательно, в день такого розыгрыша штат забирает себе 3 миллиона долларов и выплачивает игрокам 3,8 миллиона долларов: 2 миллиона долларов, которые уже есть в фонде джекпота, и 1,8 миллиона долларов, полученных от продажи лотерейных билетов в этот день. В любой отдельно взятый день то, что заработал штат, проигрывают игроки, и наоборот. Следовательно, день перераспределения призового фонда – это благоприятный день для игры в лотерею; в приведенном выше случае игроки, купившие билеты, в сумме получили от штата 800 тысяч долларов.

Если игроки покупают 3,5 миллиона билетов, складывается совсем другая ситуация. В этом случае организатор лотереи забирает свою долю в размере 2,8 миллиона долларов и выплачивает игрокам оставшиеся 4,2 миллиона долларов. Если прибавить сюда уже имеющиеся в фонде джекпота 2 миллиона долларов, получится 6,2 миллиона долларов, что меньше 7 миллионов долларов, вырученных штатом за продажу билетов. Другими словами, несмотря на щедрое перераспределение призового фонда, лотерея стала настолько популярной, что штат все равно получает прибыль за счет игроков.

Это очень радует власти штата.

Момент равновесия наступает, когда доля в размере 40 % дохода, полученного в день перераспределения призового фонда, в точности равна 2 миллионам долларов, уже поступившим в общий фонд (то есть деньги, полученные от игроков, которые были довольно неопытными или склонными к риску, чтобы играть в WinFall без перераспределения призового фонда). Это 5 миллионов долларов, или 2,5 миллиона лотерейных билетов. Но если сумма немного меньше (а за весь период существования лотереи WinFall она всегда была меньше), WinFall обеспечивает игрокам возможность заработать немного денег.

На самом деле мы используем здесь удивительный, хотя и вполне соответствующий здравому смыслу факт под названием «аддитивность ожидаемой ценности». Предположим, мне принадлежит франшиза McDonald’s и кафе, причем ожидаемая годовая прибыль от McDonald’s составляет 100 тысяч долларов, тогда как ожидаемая чистая прибыль от кафе – 50 тысяч долларов. Безусловно, в разные годы эти показатели могут повышаться и падать; ожидаемая ценность означает, что в долгосрочной перспективе средняя сумма денег, которые заработает McDonald’s, составит около 100 тысяч долларов в год, а средняя сумма денег, полученных от кафе, – 50 тысяч долларов.

Принцип аддитивности гласит, что в среднем общая сумма выручки от гамбургеров бигмак и кофе мокачино составит 150 тысяч долларов, то есть сумму ожидаемой прибыли от каждого из двух направлений бизнеса.

Другими словами, этот принцип можно сформулировать так:

аддитивность – ожидаемая ценность суммы двух величин представляет собой сумму ожидаемой ценности первой величины и ожидаемой ценности второй величины.

Математики любят записывать рассуждения такого рода в виде формулы, как мы сделали это с коммутативностью сложения (столько-то рядов с таким-то количеством отверстий – это тоже самое, что столько-то столбцов с таким-то количеством отверстий), написав формулу a × b = b × a. В данном примере, если X и Y – две величины, значение которых нам точно не известно, а E(X) – это сокращение от «ожидаемая ценность Х» (expected value of X), тогда принцип аддитивности можно записать в таком виде:

E(X + Y) = E(X) + E(Y).

Вот как это связано с лотереей. Стоимость всех билетов в отдельно взятом розыгрыше – это сумма денег, выплаченных штатом. И эта стоимость не имеет никакого отношения к неопределенности; это просто сумма денег, переданных в фонд других призовых категорий – в первом из приведенных выше примеров это 3,8 миллиона долларов. Ожидаемая ценность твердой суммы в размере 3,8 миллиона долларов составляет ровно столько, сколько вы ожидаете, – 3,8 миллиона долларов.

В этом примере в день перераспределения призового фонда в розыгрыше принимал участие один миллион игроков. Принцип аддитивности гласит, что сумма значений ожидаемой ценности всех 1,5 миллиона лотерейных билетов равна ожидаемой ценности общей стоимости всех билетов, или 3,8 миллиона долларов. Однако все билеты (во всяком случае до того, как вы узнаете выигрышные номера) имеют одну и ту же стоимость. Таким образом, вы суммируете 1,5 миллионов копий одного и того же числа и получаете 3,8 миллиона долларов; этим числом должно быть 2,53 доллара. Ваша ожидаемая прибыль на лотерейный билет составляет 53 цента, то есть более 25 % от вашей ставки – неплохая прибыль для лотереи, в которую, как принято считать, играют только простофили.

Принцип аддитивности настолько привлекателен на интуитивном уровне, что на первый взгляд может показаться, будто он очевиден. Однако, подобно определению цены пожизненных аннуитетов, он далеко не очевиден! Чтобы понять это, подставьте вместо ожидаемой ценности другие понятия – и вся схема нарушится. Возьмем хотя бы такое утверждение:

Самое вероятное значение суммы набора величин равно сумме самых вероятных значений каждой из этих величин.

Но это абсолютно ошибочное утверждение. Предположим, я случайным образом выберу, кому из троих детей оставить наследство. Самое вероятное значение доли каждого ребенка равно нулю, поскольку вероятность того, что я лишу его наследства, – два из трех. Однако самое вероятное значение суммы всех трех долей (по существу, единственно возможное значение) равно стоимости всего моего состояния.

Игла Бюффона, лапша Бюффона, окружность Бюффона

Нам придется прервать историю об университетских умниках и их игре в лотерею, поскольку, раз уж мы заговорили об аддитивности ожидаемой ценности, я не могу не рассказать вам о самом красивом из всех известных мне доказательств, основанном на той идее.

Все начинается с игры франк-карро, которая, как и генуэзская лотерея, напоминает о том, что в старые времена люди играли практически на всё. Для игры франк-карро необходима монета и пол с квадратной плиткой. Вы бросаете монету на пол и заключаете пари: упадет ли она так, чтобы полностью поместиться в пределах одной плитки или прикоснется к одному из краев плитки. Примерный перевод французского словосочетания franc-carreau на английский язык – «squarely within the square» («целиком внутри квадрата»), а в качестве монеты, которая использовалась в этой игре, выступал не франк (его тогда еще не было в обращении), а экю.

Жорж Луи Леклерк, граф де Бюффон был провинциальным аристократом из Бургундии, у которого научные амбиции возникли еще в раннем возрасте. Бюффон поступил в юридическую школу, возможно, для того чтобы вслед за своим отцом стать государственным чиновником, но сразу после окончания учебы отказался от карьеры в области права в пользу науки. В возрасте двадцати семи лет, в 1733 году, он уже был готов представить свою кандидатуру на членство в Королевской академии наук в Париже.

Впоследствии Бюффон прославился как естествоиспытатель, написав объемный труд Histoire Naturelle Générale et Particulière («Всеобщая и частная естественная история») – всего сорок четыре тома, в которых была сформулирована его теория, призванная объяснить происхождение жизни так же просто и всеобъемлюще, как теория Ньютона объяснила движение и силу. Однако на Бюффона, который еще был тогда молодым человеком, большое влияние оказала короткая встреча и долгая переписка со швейцарским математиком Габриелем Крамером, поэтому его интересы были сосредоточены в области чистой математики; именно в качестве математика он предложил свою кандидатуру в Королевскую академию наук.

В работе, представленной Бюффоном, речь шла об оригинальном совмещении двух областей математики, которые ранее считались разрозненными: геометрии и теории вероятностей. Работа была посвящена не важным вопросам механики движения планет по их орбитам или экономике великих государств, а скромной игре франк-карро. Бюффон поставил вопрос так: какова вероятность того, что монета упадет так, чтобы полностью находиться в пределах одной плитки? И каким должен быть размер напольной плитки, чтобы игра была справедливой для обоих игроков?

Вот как Бюффон сделал это. Если радиус монеты равен r, а квадратная плитка имеет сторону длиной L, тогда монета касается кромки, когда ее центр попадает внутрь меньшего квадрата со стороной L − 2r:

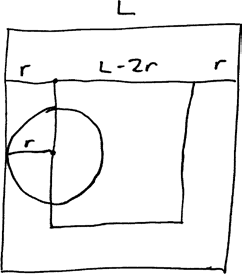
Площадь меньшего квадрата равна (L – 2r)², тогда как площадь большего квадрата – L². Следовательно, если вы заключаете пари на приземление монеты «прямо внутри квадрата», ваш шанс выиграть равен (L – 2r)² / L². Чтобы игра была справедливой, этот шанс должен быть равен 1/2, а это означает, что

(L – 2r)² / L² = 1/2.

Бюффон решил это уравнение (вы также можете его решить, если вам это интересно) и обнаружил, что игра франк-карро может быть справедливой только в случае, если сторона плитки в 4 + 2√2 раза больше радиуса монеты – коэффициент, равный почти 7. Это было интересно с концептуальной точки зрения, поскольку сочетание вероятностных рассуждений с геометрическими фигурами было совершенно новым, но эта задача была совсем не трудной, и Бюффон знал, что не она будет пропуском в академию. Поэтому он решил двигаться дальше:

«А если подбрасывать в воздух не круглую монету вроде экю, но предмет совсем иной формы: скажем, взять квадратик старинного испанского пистоля, или иглу, или какую палочку, или что еще, – тогда задача потребует немного больше геометрии».

Это было преуменьшение: задача об игле – это задача, благодаря которой имя Бюффона помнят в математических кругах даже в наше время. Позвольте мне более подробно объяснить, что именно сделал Бюффон.

Задача Бюффона об игле. Предположим, у вас есть деревянный пол, сложенный из длинных узких планок, а также игла, длина которой в точности равна ширине планок. Бросьте эту иглу на пол. Какова вероятность того, что игла пересечет одну из щелей, разделяющих планки?

Вот почему это столь щекотливая задача. Когда вы бросаете на пол экю, не имеет значения, в какую сторону смотрит отчеканенный на ней Людовик XV. Круг выглядит одинаково во всех направлениях, а значит, вероятность того, что монета пересечет край плитки, не зависит от ее ориентации.

Игла Бюффона – совсем другая история. Игла, направленная почти параллельно планкам, вряд ли пересечет край планки.

Однако, если игла упадет поперек планок, она почти наверняка пересечет щель между ними.

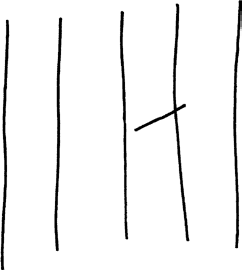
Игра франк-карро в высшей степени симметрична; если говорить в специальных терминах, она инвариантна относительно поворота монеты. В задаче об игле такая симметрия нарушена, что делает задачу гораздо более трудной: необходимо отслеживать не только место, в котором окажется центр иглы после падения, но и направление, в котором падает игла.

В двух крайних случаях вероятность того, что игла пересечет край планки, равна 0 (если игла расположена параллельно планке) или 1 (если игла расположена перпендикулярно планке). Следовательно, вы могли бы разделить разность пополам и выдвинуть предположение, что игла пересекает край планки ровно в половине случаев.

Однако это ошибочный вывод: на самом деле игла пересекает край гораздо чаще, чем падает полностью в пределах одной планки. Задача Бюффона об игле имеет неожиданное и очень красивое решение: эта вероятность составляет 2 / π, или около 64 %. Почему π, если в задаче нет никакой окружности? Бюффон нашел это решение, воспользовавшись несколько замысловатым доказательством, связанным с площадью под кривой с названием циклоида. Для того чтобы вычислить эту площадь, требуется задействовать некоторые элементы математического анализа – ничего такого, с чем не справился бы второкурсник, изучающий математику, но все же в этом нет ничего познавательного.

Однако существует еще одно решение этой задачи, которое нашел Жозеф Эмиль Барбье более чем через столетие после зачисления Бюффона в Королевскую академию наук. В этом решении формального исчисления не требуется; на самом деле вообще не нужны никакие расчеты. Доказательство, хотя и немного сложное, не требует ничего, кроме арифметической и базовой геометрической интуиции. А самое важное во всем этом – аддитивность ожидаемой ценности!

Прежде всего необходимо сформулировать задачу Бюффона в терминах ожидаемой ценности. Мы можем задать такой вопрос: чему равно ожидаемое количество краев планок, которые пересечет игла? Бюффон пытался вычислить вероятность p того, что брошенная игла пересечет край планки. Таким образом, существует вероятность 1 − p, что игла не пересечет ни одного края планки. Но если все же игла пересечет планку, то только одну. Таким образом, ожидаемое количество пересечений можно получить так же, как мы обычно вычисляем ожидаемую ценность: определив сумму каждого возможного количества пересечений, умноженного на вероятность наблюдения этого количества пересечений. В данном случае существует только два значения вероятности: 0 (наблюдаемое с вероятностью 1 − p) и 1 (наблюдаемое с вероятностью p), поэтому мы вычислим сумму

(1 – p) × 0 = 0

p × 1 = p

и получим в итоге p.

Таким образом, ожидаемое количество пересечений – это просто p, то же самое значение, которое вычислил Бюффон. Создается впечатление, что мы так и не продвинулись дальше. Как мы можем найти то загадочное число?

Когда вы сталкиваетесь с математической задачей, которую не знаете, как решить, у вас есть два основных варианта действий. Задачу можно либо упростить, либо сделать сложнее.

Первый вариант кажется более приемлемым: вы используете вместо этой задачи более простую и решаете ее в расчете на то, что понимание, обретенное вами в процессе решения более легкой задачи, поможет вам глубже проникнуть в суть более сложной задачи, которую вы пытаетесь решить. Именно это делают математики каждый раз, когда моделируют сложную реальную систему с помощью отлаженного, безупречного математического механизма. Иногда этот подход применяется весьма успешно: если вы отслеживаете траекторию движения тяжелого реактивного снаряда, вы хорошо справитесь с задачей, не принимая во внимание сопротивление воздуха и считая, что движущееся тело подвержено только постоянному воздействию силы тяжести. В других случаях ваше упрощение достигает такого уровня, что устраняет интересные аспекты задачи, как в старом анекдоте о физике, перед которым поставили задачу оптимизировать процесс производства молочных продуктов, и он без каких-либо сомнений произносит: «Возьмем сферическую корову…»

В этом духе кто-то может попытаться почерпнуть какие-либо идеи в отношении иглы Бюффона посредством решения более простой задачи с игрой франк-карро: «Возьмем круглую иглу…» Однако не совсем понятно, какую полезную информацию можно извлечь из задачи с монетой, чья вращательная симметрия лишает задачу об игле того самого свойства, которое делает ее интересной.

Вместо этого мы используем другую стратегию – стратегию, использованную Барбье: сделаем задачу более сложной. Это звучит не очень обнадеживающе. Но, когда такая стратегия работает, она работает как магическая формула.

Давайте начнем с малого. Что если мы зададим более общий вопрос: чему равно ожидаемое количество пересечений иглы с краями планки, если длина иглы составляет две ширины планки? Это вопрос кажется более сложным, поскольку теперь у нас есть три возможных результата вместо двух. Игла может упасть, полностью расположившись в пределах одной планки, или может пересечь один край планки, или может пересечь два края планки. Следовательно, чтобы вычислить ожидаемое количество пересечений, нам как будто придется вычислить вероятность трех отдельно взятых событий вместо двух.

Однако благодаря аддитивности эта более сложная проблема на самом деле легче, чем вам кажется. Нарисуйте точку посредине длинной иглы и обозначьте две половины цифрами 1 и 2, как на рисунке.

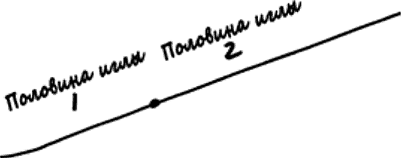
В таком случае ожидаемое количество пересечений длинной иглы равно сумме ожидаемого количества пересечений половины иглы 1 и ожидаемого количества пересечений половины иглы 2. В алгебраических терминах это можно сформулировать так: если Х – это количество краев, пересеченных половиной иглы 1, а Y – количество краев, пересеченных половиной иглы 2, тогда общее количество краев, пересеченных длинной иглой, равно X + Y. Однако каждая половина длинной иглы – это и есть игла той длины, которую изначально рассматривал Бюффон; следовательно, каждая из этих половинок иглы в среднем пересекает края планки p раз. Другими словами, E(X) и E(Y) равны p. Таким образом, ожидаемое количество пересечений целой иглы, E(X+Y), равно сумме E(X) + E(Y), что равно p + p, или 2p.

Такая же логика применима к игле, длина которой в три, в четыре или в сотню раз больше ширины планки. Если длина иглы равна N (а мы теперь берем ширину планки в качестве единицы измерения), ожидаемое количество ее пересечений равно Np.

Такой подход работает как в случае коротких, так и в случае длинных игл. Предположим, я бросаю иглу, длина которой составляет 1/2 единицы, или половину ширины планки. Поскольку иглу Бюффона длиной в 1 единицу можно разделить на две иглы длиной 1/2 единицы, ожидаемая величина p должна быть в два раза больше ожидаемого количества пересечений иглы длиной 1/2 единицы. Следовательно, ожидаемое количество пересечений иглы длиной 1/2 единицы равно (1/2)p. По существу, формула

ожидаемое количество пересечений иглы длиной N = Np

верна для любого положительного действительного числа N, будь то большого или малого.

(Здесь не стоит приводить строгое доказательство того, что представленная выше формула применима и в случае, когда N – некое страшное иррациональное число, скажем квадратный корень из 2, потому что для этого понадобятся формальные математические выкладки. Но я даю честное слово, что основные идеи доказательства Барбье – те, что я привел.)

Теперь необходимо проанализировать задачу под новым, так сказать, углом, согнув иглу.

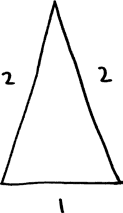
Это самая длинная игла из всех, с которыми мы до сих пор имели дело: ее общая длина равна 5 единицам. Однако эта игла согнута в двух местах, а два ее края я сомкнул, чтобы образовать треугольник. Прямые сегменты иглы имеют длину 1 единица, 2 единицы и 2 единицы; следовательно, ожидаемое количество пересечений каждого сегмента равно p, 2p и 2p соответственно. Количество пересечений всей иглы равно сумме количества пересечений каждого сегмента. Таким образом, принцип аддитивности говорит нам, что ожидаемое количество пересечений целой иглы составляет:

p + 2p + 2p = 5p.

Другими словами, формула

ожидаемое количество пересечений иглы длиной N = Np

применима и в случае согнутых игл.

Вот одна из таких игл.

Вот еще одна.

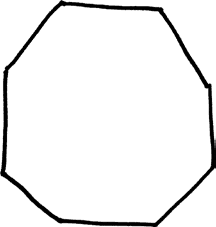
И еще одна.

Мы уже видели такие рисунки. Те самые рисунки, которые две тысячи лет назад использовали Архимед и Евдокс, когда разрабатывали метод исчерпывания. Последний рисунок похож на окружность с диаметром в одну единицу. Но на самом деле это многоугольник, состоящий из 65 536 крохотных иголок. Ваши глаза не заметят разницы, так же как не заметит ее и пол. Это означает, что ожидаемое количество пересечений окружности диаметром в одну единицу в точности такое же, что и ожидаемое количество пересечений 65536-угольника. А согласно правилу согнутой иглы, это количество равно Np, где N – это периметр многоугольника. Чему равен этот периметр? Он должен быть в точности таким же, что и длина окружности; радиус окружности равен 1/2 единицы, а значит, длина этой окружности равна π. Следовательно, ожидаемое количество пересечений окружности с краями планки равно πp.

Как вы воспринимаете такое усложнение задачи? Не кажется ли вам, что мы делаем задачу все более абстрактной и все более обобщенной, даже не ответив на основной вопрос: что такое p?

Так вот, представьте себе: мы только что вычислили это значение.

Ведь вопрос теперь звучит так: сколько пересечений делает окружность? Совершенно неожиданно задача, казавшаяся сложной, становится простой. Симметрия, которую мы потеряли, когда перешли от круга к игле, восстановлена посредством сгибания иглы в кольцо. А это существенно упрощает задачу. Не имеет значения, куда упадет круг, – он пересекает линии на полу ровно два раза.

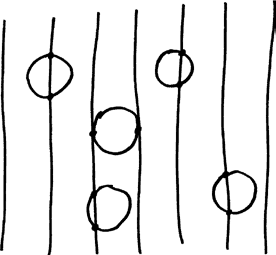
Таким образом, ожидаемое количество пересечений равно 2; оно же равно πp. Следовательно, мы можем сделать вывод, что p = 2 / π, как и говорил Бюффон. На самом деле представленная выше аргументация применима к любой игле, какой бы многосторонней или изогнутой она ни была: ожидаемое количество пересечений равно Lp, где L – это длина иглы в единицах, равных ширине планки. Бросьте на кафельный пол груду спагетти – и я смогу точно сказать, какое число пересечений линий с макаронинами следует ожидать. Математические остряки называют этот обобщенный вариант задачей Бюффона о лапше.

Море и камень

Доказательство Барбье напоминает мне слова Пьера Делиня, специалиста по алгебраической геометрии, сказанные им о своем учителе Александре Гротендике: «Кажется, будто ничего не происходит, и все-таки в итоге получается в высшей степени нетривиальная теорема».

У людей непосвященных порой складывается впечатление, что математика сводится к применению все более и более мощных инструментов для все более глубокого погружения в неизведанное, подобно тому как строители тоннелей пробиваются сквозь скалу с помощью все более мощных взрывчатых веществ. Но это только один из возможных способов. Александр Гротендик, который в 1960–1970-х годах переделал большую часть чистой математики по своему разумению, смотрел на это иначе:

Неизведанное, которое предстояло познать, казалось мне участком земли или твердого камня, сопротивляющегося вторжению… море безразлично наступает в тишине, ничего как будто не происходит, ничего не двигается, вода так далеко, что ее едва слышно… и все же в конце концов она окружает сопротивляющуюся субстанцию.

Неизведанное – это камень в море, который препятствует нашему развитию. Мы можем попытаться воткнуть динамит в щели, взорвать его и повторять все это до тех пор, пока камень не развалится на части, как сделал Бюффон со своими сложными вычислениями. Или можно придерживаться более созерцательного подхода, позволяющего вашему уровню понимания постепенно и спокойно повышаться, пока через какое-то время то, что раньше казалось препятствием, не исчезнет под спокойной водой.

Математика в современном ее виде представляет собой тонкое взаимодействие между монашеским созерцанием и взрывами динамита.

Ремарка в сторону: О математиках и безумии

Барбье опубликовал свое доказательство теоремы Бюффона в 1860 году, когда ему исполнился двадцать один год и он был многообещающим студентом Высшей нормальной школы (École normale supérieure) в Париже. В 1865 году, оказавшись на грани тяжелого нервного срыва, он уехал из города, не оставив нового адреса. Ни один математик больше не встречал Барбье, пока в 1880 году старый учитель Жозеф Бертран не нашел его в одной из психиатрических лечебниц. Что касается Гротендика, в 1980-х годах он также оставил академическую математику и живет сейчас в селинджеровском уединении где-то в Пиренеях. Никто не знает, над какими математическими задачами он работает, если вообще работает. Ходят слухи, что ученый просто пасет овец.

Эти истории перекликаются с популярным мифом о математике: что она сводит с ума или сама является одной из разновидностей помешательства. Дэвид Фостер Уоллес, самый математически образованный из всех современных прозаиков (однажды он сделал перерыв в написании художественных произведений, чтобы написать целую книгу о теории трансфинитных множеств!), называл этот миф «математической мелодрамой» и описывал его главного героя как «человека типа Прометея и Икара, высший гений которого – это также его гордыня и пагубный порок». В таких фильмах, как A Beautiful Mind («Игры разума)», Proof («Доказательство») и Pi («Пи»), математика используется в качестве символа для обозначения одержимости и бегства от реальности. А в детективе Скотта Туроу Presumed Innocent («Презумпция невиновности») сюжет построен на том, что жена главного героя, математик, оказалась психически больным убийцей. (В книге присутствует явный намек на то, что именно попытки приспособить разум женщины к математике подтолкнули убийцу к безумию.) Одну из последних версий этого мифа можно найти в романе Марка Хэддона The Curious Incident of the Dog in the Night-Time («Загадочное ночное убийство собаки»), в котором математический талант проявляется как одно из расстройств аутического спектра.

Уоллес отвергает эту мелодраматическую картину психической жизни математиков, и я согласен с ним. В реальной жизни математики – это обычные люди, не более безумные, чем все остальные. На самом деле мы не так часто уходим в уединение, чтобы вести одинокие битвы в суровых абстрактных мирах. Математика скорее укрепляет разум, а не напрягает его до предела. Как бы там ни было, я пришел к выводу, что в моменты сильных эмоциональных переживаний ничто не успокаивает поднимающуюся в душе боль лучше, чем математическая задача. Математика, подобно медитации, помогает установить прямой контакт со Вселенной, которая больше вас, которая была до вас и останется после вас. Я мог бы сойти с ума без математики.

«Они снова пытаются устроить перераспределение призового фонда»

Но вернемся к ситуации в Массачусетсе.

Чем больше людей играли в лотерею Cash WinFall, тем менее рентабельной она становилась. Каждый крупный покупатель, вступавший в игру, вынужден был делить выигрыши на большее количество долей. Джеральд Селби рассказал мне, что в какой-то момент Юран Лу из Random Strategies предложил, чтобы они с группой Селби по очереди играли в дни перераспределения призового фонда, что обеспечило бы каждой группе более высокую прибыль. Селби перефразировал предложение Юрана так: «Ты крупный игрок, я крупный игрок; мы не можем контролировать других игроков, которые как блохи в волосах». Благодаря своему сотрудничеству Селби и Лу могли бы контролировать хотя бы друг друга. Этот план имел смысл, но Селби на него не согласился. Он и без того спокойно использовал уловку в игре, поскольку ее правила были общедоступными и любой другой игрок имел возможность ознакомиться с ними точно так же, как он. Однако сговор с другими игроками (хотя и не совсем понятно, было ли это нарушением правил проведения лотереи) слишком напоминал мошенничество. В итоге три группы игроков договорились о равном участии в каждом розыгрыше лотереи с перераспределением призового фонда. По оценкам Селби, с учетом того, что при каждом таком розыгрыше крупные игроки покупали от 1,2 до 1,4 миллиона билетов, ожидаемая ценность таких билетов была на 15 % больше их цены.

Это по-прежнему была неплохая прибыль. Однако такая ситуация не удовлетворяла Харви и его сообщников. Жизнь профессионального победителя лотерей – вовсе не сплошной отдых, как вы, возможно, думаете. Для Харви руководство Random Strategies было полноценной работой, которая не приносила ему особого удовлетворения. Накануне розыгрыша с перераспределением призового фонда необходимо было купить и вручную заполнить десятки тысяч лотерейных билетов, а в день розыгрыша Харви приходилось организовывать действия многочисленных членов команды, которые сканировали все эти карточки в магазинах, согласившихся обрабатывать мегапокупки команды. А после объявления выигрышных номеров наступал длинный период кропотливой работы по отсеиванию выигрышных билетов от ничего не стоящих проигравших – и не для того, чтобы выбросить проигравшие билеты в мусор. Харви складывал их в коробки для хранения, поскольку, если вы часто выигрываете в лотерею, налоговое управление часто вас проверяет, поэтому и Харви необходимо было иметь возможность подтвердить свою игровую активность документально. (Джеральд Селби до сих пор хранит двадцать с чем-то корзин для белья, наполненных проигравшими лотерейными билетами на сумму около 18 миллионов долларов; эти корзины занимают пристройку под навесом за его домом.) Над выигрышными билетами также нужно было потрудиться. Каждый члены группы должен был заполнять индивидуальную декларацию о доходах по каждому розыгрышу, какой бы маленькой ни была его доля. Все это еще кажется вам увлекательным?

По оценкам генерального инспектора, группа Random Strategies за семилетний период существования лотереи Cash WinFall заработала на ней 3,5 миллиона долларов до вычета налогов. Неизвестно, какая часть этих денег ушла самому Джеймсу Харви, но мы точно знаем, что он купил новый автомобиль.

Это был подержанный Nissan Altima 1999 года.

Хорошие времена, когда на раннем этапе лотереи Cash WinFall можно было без труда удвоить вложенные деньги, остались в не таком уж далеком прошлом, и Харви, разумеется, хотел туда вернуться. Но как это сделать, учитывая, что семья Селби и Doctor Zhang Lottery Club покупали сотни тысяч лотерейных билетов на каждый розыгрыш с перераспределением призового фонда?

Другие крупные игроки брали перерыв только в одном случае: когда размер джекпота не позволял запустить процесс перераспределения призового фонда. Однако Харви также пропускал такие розыгрыши по той же веской причине: в таких случаях играть в лотерею было бесполезно.

В пятницу 13 августа 2010 года был объявлен джекпот на розыгрыш в следующий понедельник в размере 1,675 миллиона долларов, существенно ниже порога перераспределения суммы джекпота. Группы Чжана и Селби бездействовали в ожидании повышения джекпота до уровня перераспределения. Но группа Random Strategies затеяла другую игру. На протяжении предыдущих месяцев группа спокойно подготовила сотни тысяч дополнительных билетов в ожидании дня, когда запланированный джекпот окажется близким к 2 миллионам долларов, но все-таки не достигнет этого уровня. И вот этот день настал. Во время выходных члены группы Random Strategies объездили весь Большой Бостон, купив больше билетов, чем кто-либо покупал раньше, всего около 700 тысяч. С учетом неожиданного поступления большого объема денежных средств от Random Strategies сумма джекпота возросла в понедельник 16 августа до 2,1 миллиона долларов. Это был розыгрыш с перераспределением призового фонда, день выигрышей для игроков в лотерею, и никто кроме студентов MIT не знал, что это будет именно такой розыгрыш. Почти 90 % лотерейных билетов, проданных на этот розыгрыш, принадлежали команде Харви. Эта группа оказалась у денежного крана совершенно одна. А когда розыгрыш завершился, группа Random Strategies заработала 700 тысяч долларов на вложенных 1,4 миллиона – отличная прибыль в размере 50 %.

Этот трюк не мог сработать дважды. Как только организаторы лотереи поняли, что произошло, они внедрили систему раннего оповещения, которая должны была уведомлять руководство о признаках того, что одна из команд пытается самостоятельно поднять сумму джекпота до уровня перераспределения призового фонда. Когда в конце декабря группа Random Strategies снова предприняла такую попытку, руководство лотереи было готово к этому. Утром 24 декабря, за три дня до розыгрыша, руководитель группы по организации лотереи получил от своих подчиненных электронное письмо, в котором было сказано следующее: «Парни Cash WinFall снова пытаются устроить перераспределение призового фонда». Если Харви сделал ставку на то, что офис лотереи во время праздников работать не будет, он ошибся: ранним рождественским утром лотерея изменила запланированную сумму джекпота и объявила всему миру, что будет проведен розыгрыш с перераспределением призового фонда. Другие группы, которые еще не пришли в себя после августовского промаха, отменили свои рождественские каникулы и купили сотни тысяч билетов, вернув прибыль на нормальный уровень.

Так или иначе, игра почти исчерпала себя. Однако один знакомый Андреа Эстес, репортера Boston Globe, просматривая список победителей, публикуемый организаторами лотереи, обратил внимание на нечто интересное: в нем было много победителей лотереи в Мичигане, и все они выигрывали в одной лотерее – Cash WinFall. Открытие приятеля заставило саму Эстес задуматься: что бы все это могло значить? Как только репортер начала задаваться таким вопросом, вся картина происходящего прояснилась довольно быстро. И уже 31 июля 2011 года на первой странице Globe появилась сенсационная статья Андреа Эстес и Скотта Аллена, в которой шла речь о том, как три группы игроков монополизировали выигрыши в лотерее Cash WinFall. В августе лотерея изменила правила WinFall, установив максимальный суточный объем продаж лотерейных билетов для одной розничной точки в размере 5000 долларов, по сути заблокировав этим группам возможность покупать большое количество лотерейных билетов. Однако ущерб уже был нанесен. Если смысл лотереи Cash WinFall был в том, чтобы казаться более привлекательной для обычных игроков, то теперь она стала бессмысленной. Последний розыгрыш лотереи (как и следовало ожидать, с перераспределением призового фонда) состоялся 23 января 2012 года.

Если азартная игра вызывает у вас волнение, значит, вы ведете ее неправильно

Джеймс Харви был не первым, кто воспользовался просчетами в организации лотереи штата. Группа Джеральда Селби заработала миллионы долларов на лотерее WinFall в штате Мичиган, пока власти штата не узнали об этом и не закрыли лотерею в 2005 году. И эта практика появилась гораздо раньше. В начале XVIII столетия Франция финансировала правительственные расходы за счет продажи облигаций, но процентные ставки по этим облигациям были недостаточно высокими, чтобы стимулировать продажи. Чтобы повысить привлекательность облигаций, правительство привязало к их продаже лотерею. Каждая облигация обеспечивала ее держателю право купить билет на участие в лотерее с главным призом в размере 500 тысяч ливров – достаточно денег, чтобы можно было жить на них десятки лет. Однако заместитель министра финансов Мишель ле Пелетье де Фортс, который придумал план с лотереей, небрежно выполнил расчеты: выигрыши, которые предстояло выплачивать, существенно превышали сумму денег, которую можно было выручить за счет продажи лотерейных билетов. Другими словами, эта лотерея, подобно лотерее Cash WinFall в дни перераспределения призового фонда, имела положительную ожидаемую ценность для игроков, и любой, кто купил бы достаточное количество билетов, непременно получил бы большой выигрыш.

Единственным человеком, который это понял, оказался математик и путешественник Шарль Мари де ла Кондамин. Подобно тому как это сделал Харви почти три столетия спустя, он собрал своих друзей, организовав группу для покупки лотерейных билетов. Одним из этих друзей был молодой писатель Франсуа Мари Аруэ, больше известный как Вольтер. Хотя Вольтер не внес никакого вклада в математическую основу этой схемы, он оставил в свой след. Игроки в лотерею должны были написать на своем билете девиз, который необходимо было прочитать вслух, если билет выигрывал джекпот. Вольтер в свойственной ему манере увидел в этом прекрасную возможность для сочинения афоризмов и писал на своих билетах такие дерзкие лозунги, как «Все люди равны!» и «Да здравствует Мишель Пелетье де Фортс!», которые можно было огласить перед публикой, когда группа выигрывала приз.

Со временем представители власти все поняли и прикрыли лотерею, но это произошло уже после того, как Кондамин и Вольтер вытянули у государства такую сумму, что стали богатыми людьми на всю оставшуюся жизнь. Неужели вы думали, что Вольтер зарабатывал на жизнь написанием прекрасно составленных эссе и очерков? Тогда, как и теперь, это не позволяло разбогатеть.

Во Франции XVIII столетия не было ни компьютеров, ни телефонов, ни любых других быстрых способов передачи информации о том, кто и где покупает лотерейные билеты. Это объясняет, почему правительству понадобилось несколько месяцев, чтобы обнаружить схему Вольтера и Кондамина. Чем же могли оправдаться власти штата Массачусетс? Статья в Globe была опубликована через шесть лет после того, как организаторы лотереи впервые обратили внимание на то, что студенты покупают необычно большое количество лотерейных билетов в супермаркетах возле MIT. Разве они могли не знать о том, что происходит?

Все просто: на самом деле властям штата было известно, что происходит.

Им даже не нужно было ничего выяснять, поскольку Джеймс Харви пришел в офис лотереи в Брейнтри в январе 2005 года, еще до того как его группа сделала свою первую ставку и до того как у этой группы появилось собственное название. План Харви казался слишком хорошим, чтобы быть правдой; дело было настолько беспроигрышным, что не могло не быть какого-либо регуляторного барьера на пути к реализации плана. Харви отправился в офис лотереи, чтобы выяснить, соответствует ли его схема с покупкой большого количества лотерейных билетов правилам проведения лотереи. Неизвестно, о чем шла речь во время того разговора, но скорее всего его суть сводилась к следующему: «Конечно же, парень, попробуй». Всего через несколько недель Харви и его друзья сделали свою первую большую ставку.

Вскоре после этого в игру вступил и Джеральд Селби. Он рассказал мне, что в августе 2005 года встретился с организаторами лотереи в Брейнтри, чтобы поставить их в известность, что его компания из Мичигана будет покупать лотерейные билеты в Массачусетсе. Поэтому существование крупных игроков не было для штата секретом.

Но с какой стати властям Массачусетса позволять Харви, доктору Чжану и семье Селби выуживать у штата деньги миллионами? Какое казино позволило бы игрокам обыгрывать себя неделя за неделей, не предпринимая никаких действий?

Чтобы ответить на эти вопросы, необходимо глубже проанализировать, как на самом деле работает лотерея. Из каждых 2 долларов, вырученных от продажи лотерейного билета, штат Массачусетс оставлял себе 80 центов. Часть этих денег использовалась для выплаты комиссионных магазинам, которые продавали билеты, а также на организацию самой лотереи, а остальное передавалось в муниципальные органы власти городов по всему штату. В 2011 году почти 900 миллионов долларов ушли на оплату работы полицейских, финансирование школьных программ, а также на залатывание других дыр в муниципальном бюджете.

Оставшиеся 1,2 доллара передавались в призовой фонд, который распределялся среди игроков. Но вспомните о тех расчетах, которые мы выполнили в самом начале. В обычный день ожидаемая ценность лотерейного билета составляла всего 80 центов, а это означало, что штат в среднем возвращал игрокам по 80 центов на каждый проданный билет. Что все-таки происходит с остальными 40 центами? Здесь и вступает в игру перераспределение призового фонда. Возврат игрокам 80 центов на каждый билет не приводит к истощению призового фонда, поэтому джекпот каждую неделю увеличивается до тех пор, пока не достигнет уровня 2 миллиона долларов, после чего будет направлен на увеличение размера призов других категорий. Именно в этот момент лотерея меняет свою структуру; при этом открывается шлюз, через который все накопленные деньги перетекают в руки тех, кто окажется достаточно умным, чтобы подождать.

На первый взгляд может показаться, что в день такого розыгрыша штат теряет деньги, но это означало бы недостаточно глубоко понимать происходящее. Все эти миллионы никогда не принадлежали штату Массачусетс; они изначально были выделены на выплату призов. Штат забирает свои 80 центов с каждого проданного билета, а остальное возвращает. Чем больше билетов продано, тем больше доход штата. Штату все равно, кто выиграет. Для штата важно только то, сколько людей играет.

Таким образом, когда группы игроков обналичивали большую прибыль от билетов, купленных в день розыгрыша с перераспределением призового фонда, они забирали эти деньги не у штата, а у других игроков, особенно тех, которые столь неудачно решили сыграть в лотерею в те дни, когда перераспределения фонда не было. Эти группы игроков не обыгрывали казино. Они сами были этим казино.

Подобно другим операторам казино в Лас-Вегасе, эти крупные игроки не были полностью застрахованы от невезения. У любого игрока в рулетку может наступить полоса удачи и он выиграет у казино много денег. То же самое могло произойти и с группами игроков в лотерею, если обычный игрок угадал бы все шесть чисел, тем самым оставив в призовом фонде джекпота все те деньги, которые должны были уйти на увеличение размера призов других категорий. Однако Харви и другие крупные игроки внимательно все просчитали и пришли к выводу, что такое развитие событий маловероятно и его можно не принимать в расчет. За всю историю лотереи Cash WinFall только однажды кто-то выиграл джекпот в день розыгрыша с перераспределением призового фонда. Если вы делаете достаточно ставок со смещением вероятности выигрыша в вашу пользу, одна только величина вашего преимущества перевешивает любое невезение, с которым вы можете столкнуться.

Безусловно, это делает игру в лотерею менее волнующей. Однако для Харви и других крупных игроков смысл все этой игры был не в эмоциональном подъеме. Их подход подчинялся простому принципу: если азартная игра вызывает волнение, значит, вы ведете ее неправильно.

Если в качестве казино выступали группы игроков, то какая роль досталась штату? Штат выступал в роли… штата. Подобно тому как штат Невада взимает с казино на Стрип процент от полученной ими прибыли в обмен на поддержание инфраструктуры и регулирование, обеспечивающее процветание их бизнеса, штат Массачусетс получал свою постоянную долю от денег, которые загребали группы крупных игроков. Когда группа Random Strategies купила 700 тысяч лотерейных билетов, чтобы запустить процесс перераспределения призового фонда, города штата Массачусетс получили 40 центов из каждого билета, то есть всего 560 тысяч долларов. Штаты не любят играть в азартные игры, какой бы ни была вероятность выигрыша. Штаты любят взимать налоги. По существу, именно это и делала лотерея штата Массачусетс, причем далеко не безуспешно. Согласно отчету генерального инспектора штата, лотерея Cash WinFall обеспечила штату доход в размере 120 миллионов долларов. Когда вы уходите с добычей, которая выражается девятизначным числом, вряд ли вы будете чувствовать себя жертвой.

Так кто же все-таки стал жертвой? Очевидный ответ – другие игроки. Ведь это именно их деньги перекачивались в карманы крупных игроков. Однако генеральный инспектор штата Салливан завершает свой отчет в тоне, который предполагает, что в данной ситуации никто не стал жертвой обмана:

Поскольку организаторы лотереи объявляли широкой публике о предстоящем джекпоте в размере двух миллионов долларов, который мог запустить процесс перераспределения призового фонда, обычный игрок, покупающий один лотерейный билет или любое другое количество билетов, не оказывался в менее выгодном положении из-за крупных игроков, делающих большие ставки. Иными словами, покупка большого количества билетов крупными игроками не оказывала влияния на вероятность наличия выигрышного билета у любого другого игрока. У мелких игроков была такая же вероятность выигрыша, что и у крупных игроков. Когда джекпот превышал установленное пороговое значение и происходило перераспределение призового фонда, лотерея Cash WinFall становилась выгодной для всех, а не только для крупных игроков.

Салливан прав в том, что присутствие Харви и других крупных игроков не повлияло на вероятность того, что выигрышным станет билет другого игрока. Однако он совершает ту же ошибку, что и Адам Смит: вопрос по существу состоит не просто в том, с какой вероятностью вы можете выиграть, но и какова средняя величина ожидаемого выигрыша или проигрыша. Покупка сотен тысяч лотерейных билетов группами игроков существенно увеличила количество частей, на которые необходимо было разделить призовой фонд после перераспределения суммы джекпота, а это делает каждый выигрышный билет менее ценным. В этом смысле группы игроков причиняли ущерб обычным игрокам.

Здесь можно провести аналогию с церковной лотереей. Если почти никто не захочет принять участие в розыгрыше такой лотереи, велика вероятность, что я выиграю аж целый лоток с запеканкой. Когда на розыгрыш лотереи приходит еще сто человек, которые покупают билеты, мои шансы на выигрыш запеканки существенно снижаются. Это может сделать меня несчастным. Но разве это не справедливо? А если я узнаю, что все эти сто человек работают на одного организатора, который очень хочет заполучить всю запеканку и который вычислил, что ценность сотни лотерейных билетов на 10 % ниже розничной цены? В каком-то смысле это непорядочно, но на самом деле я не могу сказать, что чувствую себя обманутым. А с точки зрения сбора денег для церкви, который и является конечной целью всей затеи, лотерея с большим количеством участников гораздо лучше лотереи без участников.

Тем не менее, хотя крупные игроки и не являются мошенниками, в истории с лотереей Cash WinFall есть что-то неприятное. В силу своеобразных правил проведения лотереи штат сделал в итоге нечто равносильное предоставлению Джеймсу Харви лицензии в качестве владельца виртуального казино, месяц за месяцем отнимающего деньги у менее продвинутых игроков. Но значит ли это, что правила были плохими? Секретарь штата Массачусетс Уильям Гэлвин сказал в интервью Globe: «Это частная лотерея, предназначенная для знающих людей. Вопрос в том почему?»

Вернемся к цифрам – и возможный ответ напрашивается сам. Если вы помните, цель перехода к лотерее состояла в том, чтобы повысить популярность лотереи. И в этом организаторы лотереи преуспели – правда, не в такой степени, как планировалось. А если шумиха вокруг Cash WinFall стала бы настолько громкой, что каждый раз, когда наступал день розыгрыша с перераспределением призового фонда, обычные обитатели штата Массачусетс покупали 3,5 миллиона лотерейных билетов? Не забывайте, чем больше людей играет в лотерею, тем больше доля штата, равная 40 %. Как мы рассчитали раньше, если штат продает 3,5 миллиона билетов, он получает хороший доход даже в дни перераспределения призового фонда. При таких обстоятельствах покупка большого количества билетов крупными игроками больше не приносит прибыли: лазейка закрывается, группы игроков распадаются, и все, разве что кроме самих крупных игроков, остаются довольными.

Продажа такого количества лотерейных билетов была рискованным делом, но организаторы лотереи в штате Массачусетс, возможно, считали, что если им повезет, то они все-таки смогут добиться успеха. В каком-то смысле штату тоже нравилось играть в азартные игры.

Назад: Часть III Ожидание

Дальше: Глава двенадцатая Чаще опаздывайте на самолеты!