Книга: Как не ошибаться. Сила математического мышления
Назад: Глава вторая Локально прямая, глобально кривая
Дальше: Глава четвертая Сколько это в мертвых американцах?
Глава третья
Поголовное ожирение
Комический актер Евгений Мирман часто рассказывает историю, имеющую прямое отношение к статистике. По его словам, он любит повторять на своих выступлениях одну фразу: «Я читал, что сто процентов американцев – азиаты». Какой-нибудь озадаченный зритель обязательно возразит: «Но Юджин, вы же не азиат». В ответе артиста и содержится вся соль шутки: «Но я читал, что я азиат!»
Я вспомнил эту реплику Мирмана, когда натолкнулся в журнале Obesity на статью, в заголовке которой был поставлен весьма неприятный вопрос: «Будут ли все американцы страдать избыточным весом и ожирением?» Как будто одной постановки вопроса было недостаточно, в статье дается ответ: «Да – к 2048 году».
Ровно в 2048 году мне стукнет семьдесят семь, и хотелось бы верить, что в столь почтенном возрасте я все-таки останусь при своем весе и не буду страдать ожирением. Но я читал, что буду!
Статья в журнале Obesity вызвала широкие дискуссии в прессе. В новостях предупреждали о наступлении «ожирения как катастрофы современности». В Long Beach Press-Telegram была опубликована статья с простым заголовком: We’re Getting Fatter («Мы становимся все более толстыми»). Результаты исследования, проведенного автором этой статьи, перекликались с последним проявлением лихорадочной, постоянно меняющейся озабоченности американцев по поводу морального статуса нашей страны. Еще до моего рождения парни отращивали длинные волосы, а значит, мы были обречены на то, что коммунисты одержат над нами верх. Когда я был ребенком, мы слишком много играли в аркадные игры, что обрекало нас на проигрыш в конкурентной борьбе с трудолюбивыми японцами. Сейчас мы едим слишком много фастфуда, поэтому умрем слабыми и неспособными к самостоятельному передвижению, в окружении пустых пакетов от курятины, запихнутых под диваны, с которых мы уже давно не в состоянии подняться. В статье эта озабоченность была представлена в качестве научно доказанного факта.
Спешу вас обрадовать. Не все из нас в 2048 году будут страдать ожирением. Почему? Потому что не все линии прямые.
Тем не менее, как мы узнали от Ньютона, каждая линия достаточно близка к прямой. Эта идея лежит в основе линейной регрессии – статистического метода, имеющего для социологии то же значение, что и отвертка при ремонте дома. Это инструмент, которым вы почти наверняка воспользуетесь, какая бы задача перед вами ни стояла. Каждый раз, когда вы читаете в газете, что: люди, у которых много двоюродных братьев и сестер, чувствуют себя более счастливыми; граждане стран, где шире представлена сеть экспресс-кафе «Бургер Кинг», больше придерживаются свободной морали; сокращение приема ниацина повышает риск дерматофитоза в два раза; каждые 10 тысяч долларов дохода на 3 % повышают вероятность, что вы проголосуете за республиканцев, – во всех этих случаях вы имеете дело с результатом, полученным методом линейной регрессии.
Вот как это работает. Вы хотите установить взаимозависимость между двумя параметрами, скажем между стоимостью обучения в университете и средним баллом по отборочному тесту SAT принятых на учебу студентов. Возможно, вы считаете: чем выше средний балл SAT, тем дороже учебное заведение, – но посмотрите на данные, которые говорят, что это далеко не универсальный закон. В Университете Элона, расположенном на окраинах Берлингтона (штат Северная Каролина), средний совокупный результат по математике и английскому языку составляет 1217 баллов; при этом университет взимает плату за обучение в размере 20 441 доллара в год. Обучение в Колледже Гилфорда, расположенном рядом, в городе Гринсборо, обходится немного дороже – 23 420 долларов, но средний результат первокурсников по SAT составляет там всего 1131 балл.
Вместе с тем, если вы посмотрите на весь список учебных заведений Северной Каролины – тридцать один частный университет, данные об оплате за обучение и о среднем балле которых были представлены в 2007 году в «Сети ресурсов для построения карьеры штата Северная Каролина», – вы увидите четкую тенденцию.
На представленном ниже рисунке каждая точка графика соответствует одному из колледжей. Вы видите те две точки, которые находятся в правом верхнем углу, с высоким средним баллом SAT и столь же высокой платой за обучение? Это Университет Уэйк Форест и Университет Дэвидсона. Одинокая точка в нижней части рисунка соответствует единственному частному учебному заведению в этом списке, плата за обучение в котором меньше 10 тысяч долларов, – Колледжу медицинских наук Кабаррус.
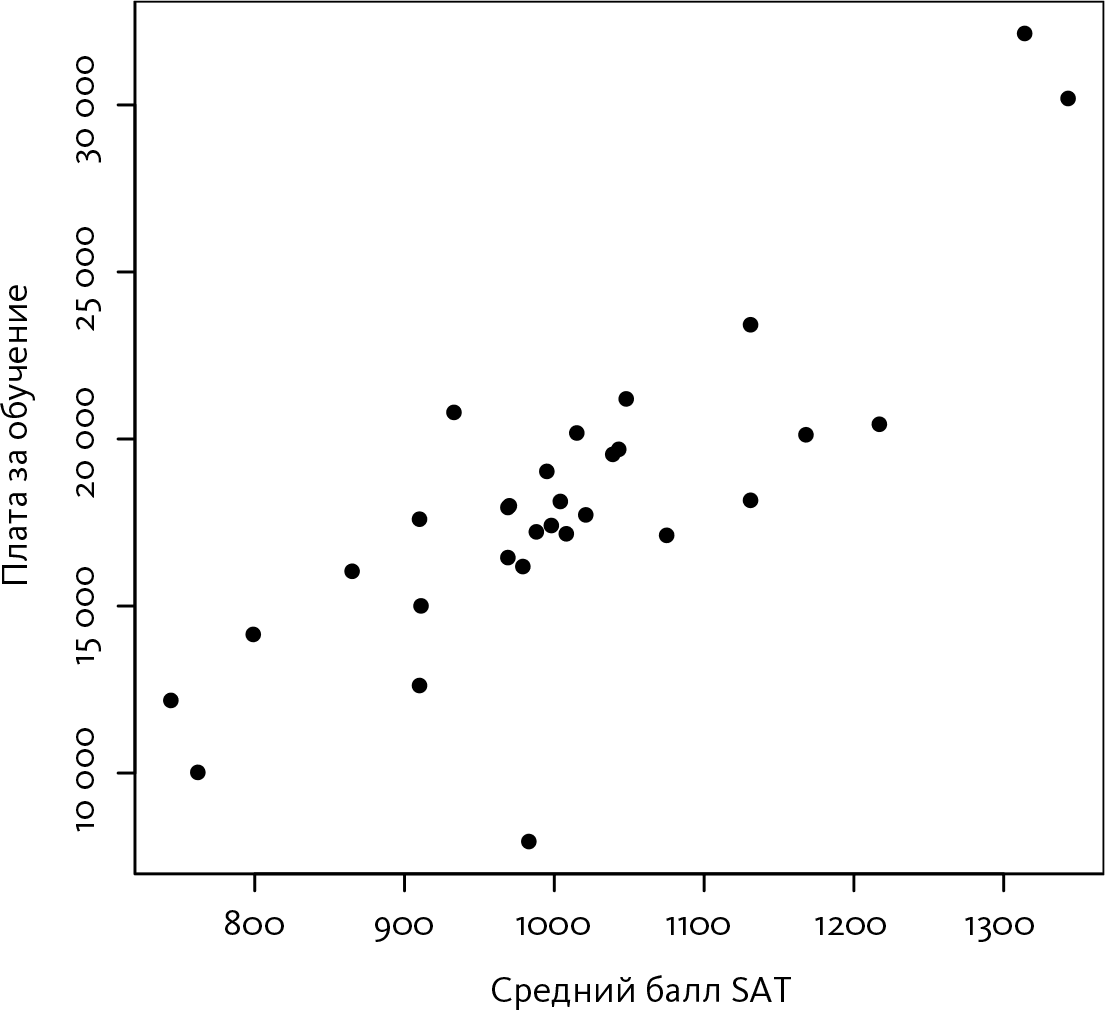
Данный рисунок четко показывает, что в учебных заведениях с более высоким средним баллом SAT цена за обучение, как правило, выше. Но насколько выше? Именно здесь на сцену выходит линейная регрессия. Очевидно, что точки на рисунке не образуют прямую линию, но видно, что они находятся не так уж далеко от прямой. Пожалуй, можно было бы вручную нарисовать прямую линию, проходящую посередине этого облака точек. Линейная регрессия исключает угадывание и позволяет найти прямую линию, максимально приближенную ко всем точкам. В случае университетов штата Северная Каролина эта прямая выглядит так, как на следующем рисунке.
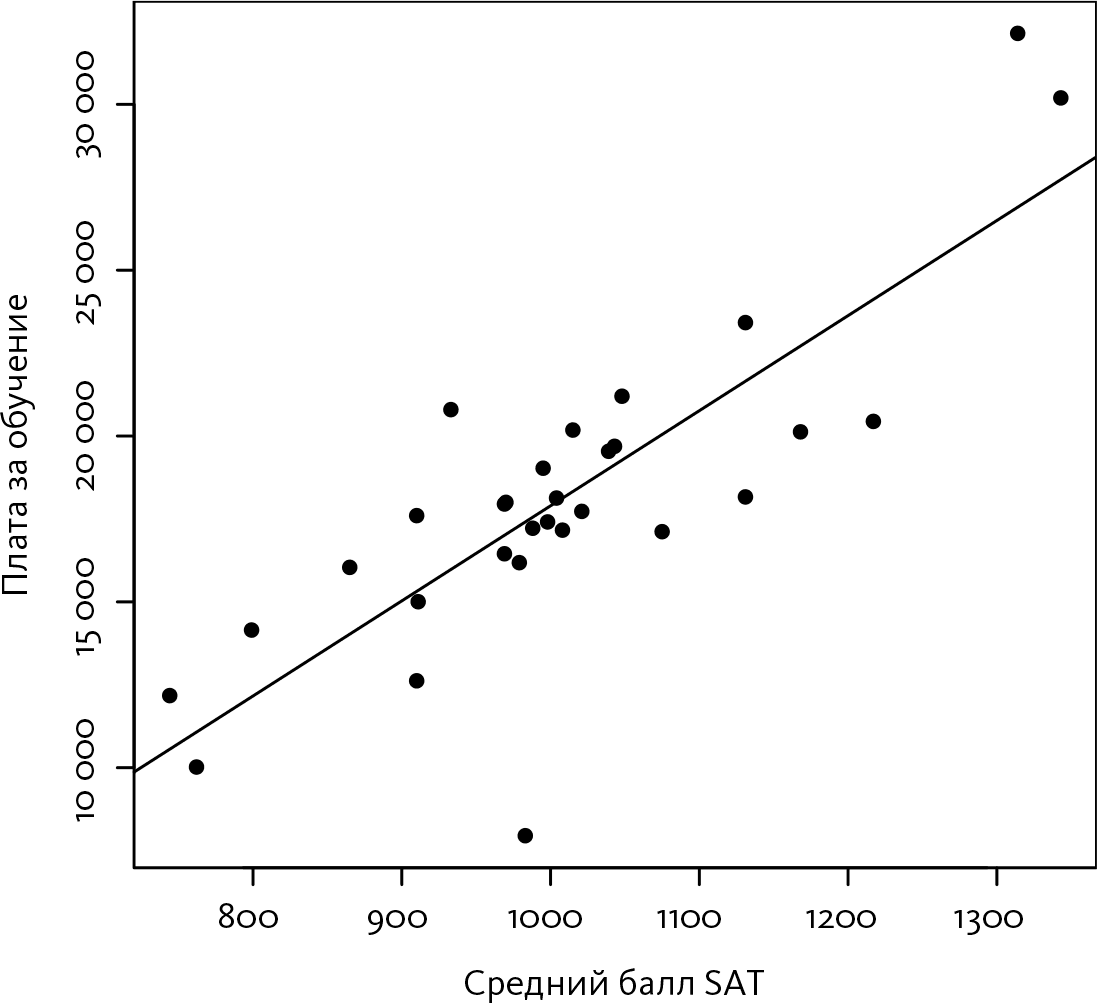
Коэффициент наклона изображенной на рисунке прямой равен 28. Это означает следующее: если плата за обучение зависела бы только от баллов SAT, которые задает прямая на графике, тогда на каждый балл SAT приходилось бы дополнительных 28 долларов платы за обучение. Если вам удалось бы поднять средний балл первокурсников на 50 пунктов, тогда вы могли бы назначить более высокую плату за обучение – на 1400 долларов. (Или, с точки зрения родителей, если ваш ребенок на 100 баллов улучшит свой результат отборочного теста, это обойдется вам в дополнительных 2800 долларов в год. Курс по подготовке к тесту оказался более дорогим, чем вы думали!)
Линейная регрессия представляет собой замечательный инструмент: гибкий, масштабируемый и легкий в применении (вы просто нажимаете соответствующую кнопку электронной таблицы). Этот инструмент можно применять к двум наборам данных с участием двух переменных, как в приведенном выше примере, но он работает не менее эффективно и в случае трех или даже тысячи переменных. Каждый раз, когда вам нужно понять, как одни переменные меняют другие переменные и в каком направлении, линейная регрессия – это первое, что следует использовать. Этот инструмент применим буквально к любому набору данных.
Однако в этом заключается не только сильная, но и слабая сторона линейной регрессии. Вы можете применить этот метод, не задумываясь, действительно ли феномен, который вы пытаетесь моделировать, близок к линейному. Но вы не должны так делать. Я сказал, что линейная регрессия подобна отвертке – что действительно так; однако в другом смысле она скорее напоминает циркулярную пилу. Если вы примените этот инструмент без тщательного анализа того, что вы делаете, результаты могут оказаться плачевными.
Возьмем в качестве примера ракету, которую мы с вами запустили в предыдущей главе. Возможно, вы не имеете никакого отношения к ее запуску. А может быть, напротив, представляете собой ту цель, на которую эта ракета направлена. В последнем случае вы особенно заинтересованы в как можно более точном анализе траектории движения ракеты.
Вы могли бы нанести на график положение ракеты по вертикали в пяти точках по времени. Такой график выглядит следующим образом.

Теперь вы в состоянии быстро выполнить линейную регрессию, получив замечательный результат: линию, которая проходит почти через все точки на графике.

(В этот момент ваша рука начинает приближаться к острому полотнищу циркулярной пилы.)
Построенная вами линия представляет собой весьма точную модель движения ракеты: за каждую минуту ракета поднимается вверх на определенное фиксированное расстояние, скажем на 400 метров. Через час ракета окажется в 24 километрах над поверхностью земли. Когда же она опустится на поверхность? Никогда! Направленная вверх наклонная прямая линия по-прежнему стремится вверх. Именно так ведут себя прямые.
(Кровь, травмы, вопли.)
Однако не каждая линия является прямой. А траектория полета ракеты несомненно представляет собой не прямую, а параболу. Подобно окружности Архимеда, вблизи она действительно похожа на прямую, поэтому линейная регрессия сослужит вам большую службу, позволив определить местоположение ракеты через пять секунд после запуска. Но через час? Даже не думайте об этом. Ваша модель говорит о том, что через час ракета находится в нижних слоях стратосферы, хотя на самом деле она, возможно, уже приближается к вашему дому.
Возможно, самое образное предостережение в отношении бездумной линейной экстраполяции сформулировал не статистик, а Марк Твен в романе Life on the Mississippi («Жизнь на Миссисипи»):
…Длина Миссисипи между Каиром и Новым Орлеаном сто семьдесят шесть лет тому назад была тысяча двести пятнадцать миль. После прорыва русла в 1722 году длина стала тысяча сто восемьдесят миль. Когда образовался рукав у Американской излучины, длина стала тысяча сорок миль. С тех пор этот участок реки укоротился еще на шестьдесят семь миль. Следовательно, сейчас ее длина между Каиром и Новым Орлеаном всего девятьсот семьдесят три мили.…За сто семьдесят шесть лет Нижняя Миссисипи укоротилась на двести сорок две мили, то есть в среднем примерно на милю и одну треть в год. Отсюда всякий спокойно рассуждающий человек, если только он не слепой и не совсем идиот, сможет усмотреть, что в древнюю силурийскую эпоху, – а ей в ноябре будущего года минет ровно миллион лет – Нижняя Миссисипи имела свыше миллиона трехсот тысяч миль в длину и висела над Мексиканским заливом наподобие удочки. Исходя из тех же данных, каждый легко поймет, что через семьсот сорок два года Нижняя Миссисипи будет иметь только одну и три четверти мили в длину, а улицы Каира и Нового Орлеана сольются, и будут эти два города жить да поживать, управляемые одним мэром и выбирая общий городской совет. Все-таки в науке есть что-то захватывающее. Вложишь какое-то пустяковое количество фактов, а берешь колоссальный дивиденд в виде умозаключений. Да еще с процентами.
Ремарка в сторону: Как получить зачетные баллы на моем экзамене по математическому анализу
Методы математического анализа во многом похожи на линейную регрессию: они носят сугубо механический характер, с ними вполне может справиться ваш калькулятор, а невнимательное применение этих методов сопряжено с большими опасностями. На экзамене по матану вам могут предложить рассчитать вес воды, оставшейся в кувшине после того, как вы проделаете в нем отверстие и позволите воде вытекать определенным потоком на протяжении определенного промежутка времени, и тому подобное. Решая задачу такого рода в условиях нехватки времени, вполне можно сделать арифметические ошибки. Порой это приводит к тому, что тот или иной студент получает нелепый результат, например что вес воды в кувшине составляет −4 грамма.
Если студент получает результат «−4 грамма» и в отчаянии торопливо пишет «Я где-то напортачил, но не могу найти ошибку», я даю такому студенту половину зачетных баллов за экзамен.
Если же студент просто пишет «−4 грамма» в конце страницы и обводит этот результат кружком, он получает ноль зачетных баллов – даже если вся процедура вывода этого результата была правильной, за исключением того, что где-то посередине страницы единственная цифра оказалась не на своем месте.
Вычисление интеграла или выполнение линейной регрессии – это задачи, которые достаточно эффективно может решать компьютер. Понимание того, имеет ли полученный результат смысл (или принятие решения, стоит ли вообще применять соответствующий метод в данном случае), требует направляющей человеческой руки. Когда мы преподаем математику, предполагается, что нужно объяснить учащимся, как стать таким проводником. Курс математики, который не делает этого, по существу учит студента выполнять функции дефектной версии Microsoft Excel.
Будем откровенны: именно это и происходит на большинстве наших математических курсов. Сокращенная история споров (сама представляющая собой предмет споров) состоит в том, что преподавание математики детям вот уже несколько десятилетий является ареной так называемых математических войн. По одну сторону этого противостояния находятся учителя, которые предпочитают делать акцент на запоминании, беглости, традиционных алгоритмах и точных ответах, а по другую сторону – учителя, считающие, что в основе преподавания математики должно лежать выяснение смысла, развитие способов мышления, обучение методом направляемых открытий и аппроксимация. Первый подход называют порой традиционным, а второй – реформистским, хотя предположительно нетрадиционный подход к обучению посредством открытий используется в той или иной форме вот уже десятки лет, а действительно ли так называемые реформы можно считать реформами – это и есть предмет споров. Споров весьма ожесточенных. Во время званого математического ужина вполне прилично обсуждать политические или религиозные вопросы, но начните спорить о математической педагогике – и это грозит закончиться тем, что кто-то из сторонников либо традиционного, либо реформистского подхода обидится и хлопнет дверью.
Я не причисляю себя ни к одному из этих лагерей. Мне не по пути с теми реформистами, которые хотят отказаться от заучивания таблицы умножения наизусть. В процессе серьезных математических размышлений вам неизбежно понадобится умножить 6 на 8, но, если каждый раз для этого доставать калькулятор, вам не удастся достичь того состояния интеллектуальной спонтанности, которая требуется для процесса размышлений. Нельзя написать сонет, выискивая в словаре значение каждого слова.
Некоторые сторонники реформистского подхода заявляют, что классические алгоритмы (например, «сложить два двузначных числа, расположив одно над другим столбиком и в случае необходимости выполнив перенос») следует исключить из учебного курса, чтобы они не мешали ученикам самостоятельно обнаруживать свойства математических объектов.
С одной стороны, я считаю эту мысль ужасной: такие алгоритмы представляют собой полезные инструменты, над разработкой которых кто-то упорно работал, и нет никаких оснований начинать все с нуля.
С другой стороны, мне кажется, что в современном мире вполне можно отказаться от некоторых алгоритмов. Например, нам нет необходимости учить студентов извлекать квадратные корни вручную или в уме (хотя второй из этих двух навыков, говорю вам по собственному опыту, можно использовать в качестве замечательного фокуса на вечеринке в кругу яйцеголовых). Калькулятор – не менее полезный инструмент, над созданием которого кто-то упорно трудился; мы также должны использовать этот инструмент, когда того требует ситуация! Меня даже не интересует, могут ли мои студенты разделить 430 на 12 посредством деления столбиком. Меня на самом деле волнует лишь одно: они должны мысленно определить, что ответ немногим больше 35 – тогда я буду спокоен, что у них прекрасно развиты арифметическое мышление и представление о числах.
Опасность чрезмерного акцента на алгоритмах и точных вычислениях состоит в том, что к ним слишком легко получить доступ. Если мы остановимся на видении математики как дисциплины, которая сводится к «получению правильного ответа» и не более того, мы начнем тестировать абитуриентов на наличие только этой способности и рискуем тем, что будем воспитывать студентов, которые получают по тестам отличные результаты, но совсем не знают математики. Может быть, это устраивает тех, кого интересуют одни лишь результаты тестов, но это не устраивает меня.
Безусловно, совсем не лучше – на самом деле даже гораздо хуже – создавать популяцию студентов, у которых сформировалось некое понимание математического смысла, но не умеющих быстро и правильно решать примеры. Преподаватели математики больше всего не любят слышать от студентов заявления такого рода: «Я понимаю концепцию, но не умею решать задачи». Возможно, такие студенты даже не догадываются, что их фраза подразумевает следующее: «Я не понимаю концепции». Математические идеи могут казаться абстрактными, но они имеют смысл только в контексте конкретных вычислений. Уильям Карлос Уильямс сформулировал эту мысль так: «Нет идей вне вещей».
Эта борьба нигде не проявляется более отчетливо, чем в планиметрии. Здесь находится последний бастион обучения построению доказательств, которые лежат в основе преподавания математики. Многие профессиональные математики считают доказательство последним оплотом «истинной математики». Однако не совсем понятно, в какой степени мы на самом деле учим красоте, силе и неожиданности доказательства в процессе преподавания геометрии. Учебный курс легко может превратиться в рутинную отработку таких бесполезных и неинтересных задач, как вычисление тридцати определенных интегралов. Это настолько серьезная ситуация, что лауреат Филдсовской премии Дэвид Мамфорд предположил: мы можем полностью отказаться от планиметрии, заменив ее начальным курсом программирования. Компьютерная программа имеет много общего с геометрическим доказательством: и то и другое требует, чтобы студент собрал один за другим воедино ряд простых элементов, выбранных из небольшой совокупности вариантов, так, чтобы в целом сформированная последовательность выполняла ту или иную значимую задачу.
Я не настолько радикален. Я вообще не отношусь к числу радикалов. Хотя это и может вызвать недовольство сторонников обоих подходов, я считаю, что мы должны преподавать математику, в которой высоко ценятся как точные ответы, так и интеллектуальная аппроксимация; математику, требующую как способности свободно применять существующие алгоритмы, так и простого здравого смысла, помогающего находить спонтанные решения; математику, в которой научная строгость сочетается с ощущением игры. Откровенно говоря, если всего этого нет, мы вообще преподаем не математику.
Трудная задача, но именно этим занимаются лучшие преподаватели математики, пока наверху среди администраторов бушуют математические войны.
И снова об ожирении – этой катастрофе современности
Так сколько американцев будут страдать ожирением к 2048 году? Вы уже догадываетесь, как Юфа Ванг и другие авторы статьи, опубликованной в журнале Obesity, построили свою проекцию. Национальная программа проверки здоровья и питания населения (National Health and Nutrition Examination Study, далее везде – NHANES) отслеживает данные о состоянии здоровья большой репрезентативной выборки граждан, охватывающие самые разные аспекты: от потери слуха до передачи инфекций половым путем. В частности, NHANES предоставляет весьма достоверные данные о доле американцев, имеющих избыточный вес; его в данном случае можно определить как вес, при котором индекс массы тела (далее везде – ИМТ) равен 25 и более. Нет никаких сомнений в том, что за последние десятилетия распространенность избыточного веса увеличилась. В начале 1970-х годов чуть менее половины американцев имели столь высокий ИМТ. В начале 1990-х этот показатель возрос до 60 %, а в 2008 году избыточный вес был почти у трех четвертей населения США.
Вы можете самостоятельно построить график роста распространенности ожирения во времени, как мы сделали это с вертикальным перемещением ракеты.
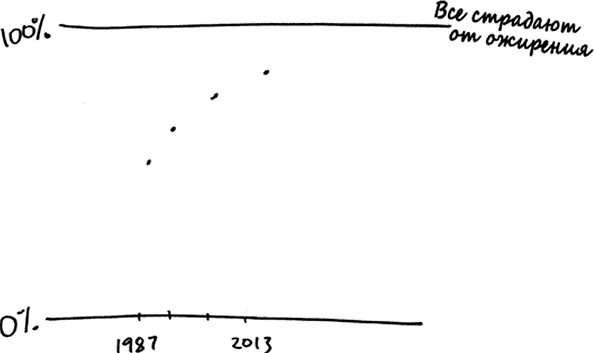
Далее вы можете сформировать линейную регрессию, которая будет выглядеть примерно так.
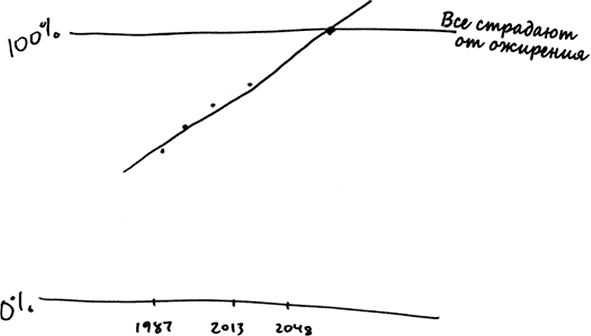
Прямая линия пересечет уровень 100 % в 2048 году. Именно поэтому Ванг пишет, что к 2048 году все американцы будут страдать избыточным весом, если текущая тенденция сохранится.
Но текущая тенденция не сохранится. Это просто невозможно! Если было бы так, то к 2060 году уже 109 % американцев имели бы избыточный вес.
В действительности график, отображающий рост доли людей с избыточным весом, изгибается к 100 % следующим образом.
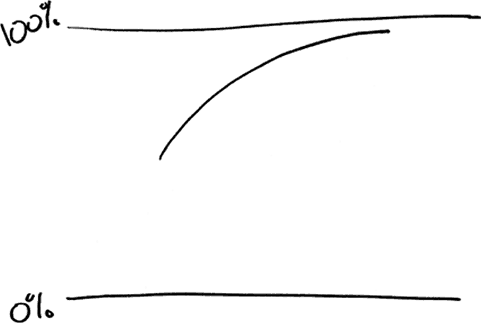
Этот закон отнюдь не незыблем, как и в случае, когда сила тяжести изгибает траекторию движения ракеты в виде параболы, однако он близок к реальности с медицинской точки зрения. Чем больше доля людей с избыточным весом, тем меньше остается худощавых людей, которые могли бы стать толстыми, и тем медленнее доля людей с избыточным весом приближается к 100 %. На самом деле в какой-то точке ниже 100 % эта кривая перейдет в горизонтальную линию. Худые всегда будут с нами! В действительности четыре года спустя по результатам опроса NHANES было установлено, что распространенность избыточного веса начала замедляться.
Однако статья в журнале Obesity скрывает еще худшее преступление против математики и здравого смысла. Сделать линейную регрессию довольно легко – и как только вы выполнили ее один раз, возникает соблазн делать это и дальше. Поэтому Ванг и его коллеги разбили свои данные на категории по этнической и половой принадлежности. Например, оказалось, что чернокожие мужчины с меньшей вероятностью имеют избыточный вес, чем американцы в целом. Еще важнее, что среди чернокожих мужчин количество людей с избыточным весом увеличивалось в два раза медленнее. Если мы отобразим на одном рисунке графики увеличения доли людей с избыточным весом среди чернокожих мужчин и среди всех американцев, а также линейную регрессию, построенную Вангом и его коллегами, получится следующая картина.
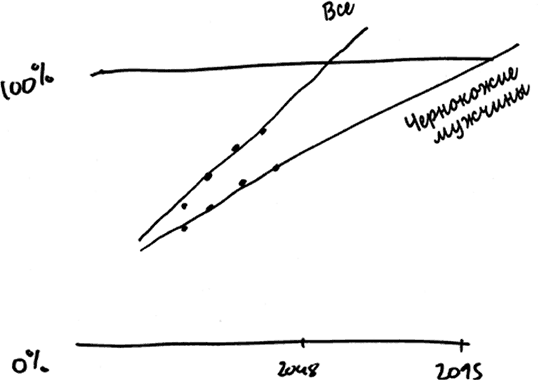
Молодцы, чернокожие! Вы не будете жирными вплоть до 2095 года, а в 2048 году ожирение распространится лишь у 80 %.
Видите, в чем проблема? Если предполагается, что в 2048 году все американцы будут иметь избыточный вес, где же будут те чернокожие мужчины, у которых не возникнет в будущем никаких проблем с весом? За пределами страны?
В статье это противоречие осталось без внимания. А ведь это эпидемиологический эквивалент утверждения о −4 граммах воды в кувшине. Ноль зачетных баллов.
Назад: Глава вторая Локально прямая, глобально кривая
Дальше: Глава четвертая Сколько это в мертвых американцах?

