Когда я тусовался с парнями в нагуталиненных ботинках, то умудрился завалить алгебру. Причина? Не выучил таблицу для запоминания тригонометрических функций. К моему сожалению, большинство из тех, кто занимается теорией комплексных систем, выражают свои мысли при помощи уравнений, а мой мозг реагирует на это так же, как на быструю итальянскую речь (тут же вспоминается сцена, когда мы стояли на железнодорожной платформе в Италии и пытались хоть что-то понять из объявления по громкоговорителю: «II treno per Firenze e appena partire al binario due; il treno di Milano e appena arrivare al binario cuatro; il treno di Venezia...» («Поезд во Флоренцию отправляется в... поезд из Милана прибывает в... поезд из Венеции...»)).

Но к моей радости, концепцию самоорганизации можно понять без всяких уравнений (и без итальянского), просто посмотрев на рисунки. Я был поражен, когда обнаружил, что самоорганизация предстает прямо перед глазами, если воспользоваться простой компьютерной программой составления таблиц. Как-то вечером, наслушавшись, как Гай Ван Орден и моя коллега Сэнди Брэйвер обсуждают исследование Латанэ о распространении влияний в группах, я пришел домой и нарисовал на экране простую матрицу, состоящую из черных, белых и серых элементов, такую, как на рис. 12.1.

Представьте себе такую картину: соседям нужно проголосовать по поводу введения специального налога на строительство новой школы. Давайте предположим, что поначалу мы имеем разброс мнений, то есть они распределены произвольно по отношению друг к другу. Предположим также, что потом ваши соседи начинают обсуждать вопрос с соседями, живущими поблизости, и приходят к мысли, что не будут поддерживать позицию, не пользующуюся популярностью. После того как я изобразил это схематически, подобно тому, как это сделано на рис. 12.1, я задал такие параметры в программе Excel, которая автоматически обновляла решение каждого соседа с учетом общего изначального мнения близких соседей.

После первого этапа обсуждения сосед из третьего дома внизу слева изменил свою позицию с отрицательного ответа на положительный, а кое-кто из его соседей, наоборот, изменил «да» на «нет». Окончательная раскладка всегда отличалась от начальной и зависела от того, на какой случайной схеме я первый раз включил свой компьютер. Тем не менее всего после нескольких обновлений крапчатая структура исчезала, вся схема как-то упрощалась и приобретала более однородный вид. В этом случае, если каждый сосед в конце концов принимал решение согласиться с большинством, все соседи оказывались объединенными в оппозицию и схема выглядела таким образом, как в квадрате Сценарий 1.

Системы, подобные этой, вначале очень нестабильны, и даже самые незначительные различия на начальном этапе могут оказать огромное влияние на вид окончательного соотношения. Например, в Сценарии 2 (правый верхний квадрат) изображено, что произойдет, если всего лишь один человек (отмечен серым) не согласится с большинством, а будет настроен скорее голосовать «за». Этот человек, к примеру Альберта, изменила бы «да» на «нет», только если бы ее соседи были единогласно против; но если хоть один был бы готов голосовать «за», Альберта тоже не изменила бы свое решение и проголосовала «за». Этот отдельно взятый одиночка с собственным мнением в этом случае оказывает такое большое влияние, что постепенно все соседи делятся на два лагеря (Сценарий 2) — южный лагерь, готовый голосовать «за», и северный — «против». На нижнем правом квадрате (Сценарий 3) видно, что произойдет, если в северном лагере появится одиночка, назовем ее Агнесс (тоже отмечена серым), с положительным мнением. Эти двое смогли бы полностью изменить единодушное решение соседей.

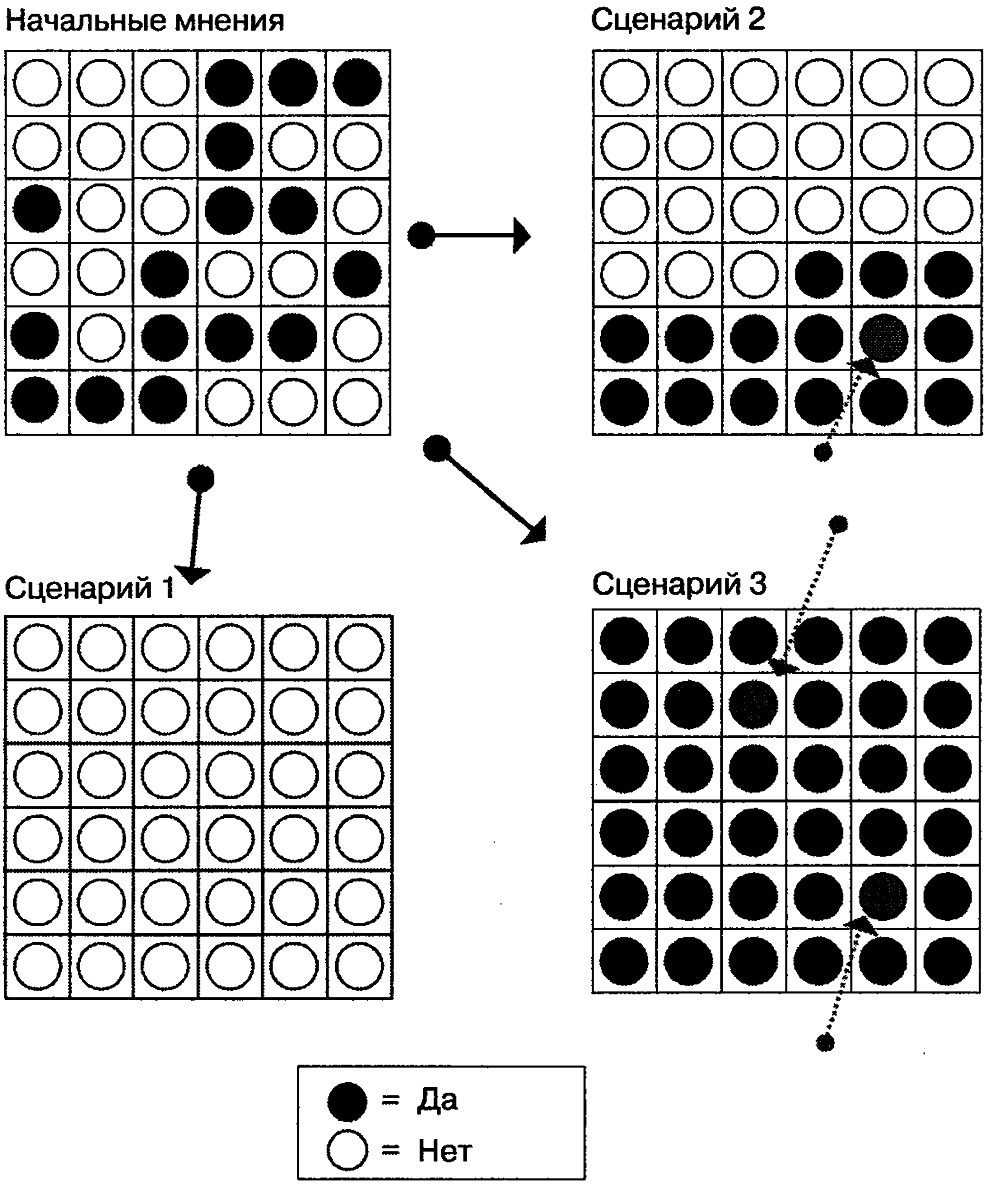
Рис. 12.1. Самоорганизация соседей. Верхний левый квадрат — это соседи, у которых разделились мнения по какому-то вопросу. Учитывая, что каждый из них хочет примкнуть к большинству, то через несколько раундов переговоров непосредственные соседи все по очереди присоединятся к оппозиции. Если один или двое соседей твердо придерживаются более подходящей, с их точки зрения, позиции (это серые одиночки справа), то окончательная картина может выглядеть совершенно иначе (как описано в тексте)

Обратите внимание, что хотя вначале было невозможно предсказать результат, потому что система была крайне неустойчивой, его очень сложно изменить после того, как система стабилизировалась. Если бы Альберта и Агнесс уехали из города на момент первого промежуточного обсуждения, то результаты получили бы устоявшийся вид, как в Сценарии 1. А когда Агнесс и Альберта вернулись бы, они обе согласились бы с единодушным мнением соседей голосовать «против». Но если бы система пришла в равновесие с единогласной поддержкой выдвинутой идеи всеми соседями, как в Сценарии 3, то позиция всех осталась бы неизменной, даже если бы обе женщины потом отсутствовали.