Книга: Теория относительности Эйнштейна за 1 час
Назад: «Год чудес»: невероятные открытия молодого ученого
Дальше: О двойственной природе света: вклад Эйнштейна в квантовую теорию
Никакого эфира нет: специальная теория относительности
О принципе относительности говорил еще известный физик и астроном Галилео Галилей в XVI веке. В трактате «Диалог о двух главнейших системах мира» он предложил читателям такой эксперимент: «Уединитесь с кем-либо из друзей в просторном помещении под палубой какого-нибудь корабля, запаситесь мухами, бабочками и другими подобными мелкими летающими насекомыми; пусть будет у вас там также большой сосуд с водой и плавающими в нем маленькими рыбками; подвесьте далее наверху ведерко, из которого вода будет капать капля за каплей в другой сосуд – с узким горлышком, подставленный внизу.
Пока корабль стоит неподвижно, наблюдайте прилежно, как мелкие летающие животные с одной и той же скоростью движутся во все стороны помещения; рыбы, как вы увидите, будут плавать безразлично во всех направлениях; все падающие капли попадут в подставленный сосуд, и вам, бросая другу какой-нибудь предмет, не придется бросать его с большей силой в одну сторону, чем в другую, если расстояния будут одни и те же; и если вы будете прыгать сразу двумя ногами, то сделаете прыжок на одинаковое расстояние в любом направлении.
Прилежно наблюдайте все это, хотя у нас не возникает никакого сомнения в том, что, пока корабль стоит неподвижно, все должно происходить именно так. Заставьте теперь корабль двигаться с любой скоростью, и тогда (если только движение будет равномерным и без качки в ту и другую сторону) во всех названных явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли корабль или стоит неподвижно… И причина согласованности всех этих явлений в том, что движение корабля обще всем находящимся в нем предметам, также как и воздуху; поэтому-то я и сказал, что вы должны находиться под палубой…»
В сегодняшней физике принцип относительности сформулирован так: во всех инерциальных системах отсчета (находящихся в неподвижности или движущихся равномерно и прямолинейно) механические явления происходят одинаково, по одним и тем же законам.
Чтобы понять важность такого фактора, как система отсчета, можно рассмотреть эксперимент Галилея с точки зрения геометрии. Представим, что на причале стоит наблюдатель, фиксирующий движение корабля. Ему будет соответствовать первая, неподвижная система отсчета. Второй наблюдатель и вторая система отсчета – движущаяся – находятся в трюме.
Если корабль движется вдоль причала с постоянной скоростью, то положение в пространстве второго наблюдателя изменяется, но он этого не знает. Он определяет свои координаты как находящиеся на нулевой отметке оси координат. Первый наблюдатель видит, как меняется положение второго, и может определить его координаты на своей оси. Они будут отличаться от нулевой отметки на то расстояние, которое преодолел второй наблюдатель. Для того чтобы получить возможность связать между собой первую и вторую систему отсчета, были созданы преобразования Галилея, представляющие собой систему несложных уравнений. Они позволяют перевести координаты из одной системы отсчета в другую. В нашем случае первый наблюдатель, чтобы определить местоположение второго, прибавляет расстояние, которое тот проделал. Второй же для определения местоположения первого должен это расстояние вычесть.
Если пойти дальше, можно задуматься о том, что первый наблюдатель не неподвижен, он движется вместе с планетой Земля вокруг Солнца – это уже третья система отсчета. Солнце тоже не стоит на месте, оно вместе с другими звездами вращается вокруг цента Млечного Пути. Таким образом, систем отсчета может быть бесконечное количество. Движущийся корабль, с которого начался эксперимент, в каждой из этих систем отсчета будет иметь разные траектории, все более усложняющиеся по мере перехода из одной системы отсчета в другую. И для каждой из систем отсчета будут верны законы Ньютона и его формулы. Классическая динамика работает независимо от того, в какой системе находится объект, покоится он или движется, – в этом и заключается суть принципа относительности Галилея.
После того как Максвелл в XIX веке создал уравнения, описывающие электромагнитные взаимодействия, было обнаружено, что они противоречат законам Ньютона и принципу относительности Галилея. При переводе уравнений из одной системы отсчета в другую (с использованием преобразований Галилея) они, в отличие от законов Ньютона, изменялись. При переходе в движущуюся систему координат в них появлялись новые элементы, соответствующие странным физическим явлениям. К примеру, линии магнитного поля, которые в неподвижном состоянии неразрывны, при движении, в соответствии с уравнениями, становились прерывистыми.
Так как преобразования Галилея не справлялись с электромагнитными уравнениями Максвелла, нужны были другие уравнения. Их после многолетней работы вывел Хендрик Лоренц. Уравнения Лоренца позволяли перевести формулы Максвелла из одной системы координат в другую без усложнения и появления новых элементов. Главное отличие преобразований Лоренца от уравнений Галилея заключалось во введении дополнительного параметра – скорости.
Необходимо отметить, что если скорости исследуемых объектов намного меньше скорости света, то преобразования Лоренца трансформируются в преобразования Галилея. Таким образом, в привычной, обыденной реальности продолжают работать законы Ньютона, хорошо всем понятные. Более сложные теории, в том числе и специальная теория относительности Эйнштейна, работают в сфере сверхвысоких скоростей, с которыми мы в повседневности не сталкиваемся. Именно поэтому нам так сложно понять эти теории и вытекающие из них следствия.
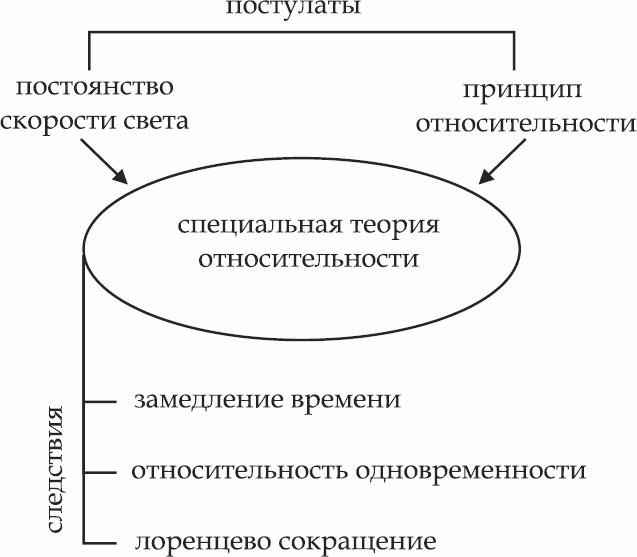
Схема специальной теории относительности
Уравнения Лоренца были лаконичны, удобны для расчетов, но у них обнаружились своеобразные «побочные эффекты»: из преобразований получалось, что любому конкретному моменту в неподвижной системе отсчета соответствовало бесконечное количество моментов в системе движущейся. То есть события теряли свойство одновременности. Кроме того, получалось, что тела при движении должны сжиматься в направлении движения. А время в движущихся системах отсчета замедлялось. Чтобы объяснить все эти, как тогда казалось, недоразумения, ученые обратились к изучению эфира.
В то время общепринятым было мнение, что любые волны должны распространяться в какой-то среде (к примеру, как звуковая волна распространяется по воздуху). В соответствии с уравнениями Максвелла свет является волной, ученые считали, что среда, в которой он распространяется, – это эфир. Было поставлено множество опытов, которые должны были подтвердить существование эфира, но все тщетно. Эфир казался неуловимым.
Именно в этот момент на научной сцене появился Эйнштейн.
Теории Эйнштейна возникли не на пустом месте, они были подготовлены открытиями череды ученых, начиная с Галилея и Ньютона и заканчивая Лоренцем и Пуанкаре.
«Если смотреть на развитие теории относительности ретроспективно, – говорил Эйнштейн, – то в 1905 году она готова была к тому, чтобы ее открыли». Он был уверен, что уравнения Максвелла идеальны, то, что они разрушаются при смене системы отсчета, казалось ему ошибкой. Для того чтобы ее обнаружить и устранить, он сосредоточился на главном, как он считал, факторе электромагнитных явлений – относительном движении. Свою статью «К электродинамике движущихся тел» Эйнштейн начал такими словами: «Известно, что электродинамика Максвелла в современном ее виде приводит в применении к движущимся телам к асимметрии, которая несвойственна, по-видимому, самим явлениям. Вспомним, например, электродинамическое взаимодействие между магнитом и проводником с током. Наблюдаемое явление зависит здесь только от относительного движения проводника и магнита, в то время как, согласно обычному представлению, два случая, в которых движется либо одно, либо другое из этих тел, должны быть строго разграничены».
Все заключения, высказанные в революционной статье Эйнштейна, основывались на двух постулатах: законы физики принимают один и тот же вид во всех системах отсчета, где движение является равномерным; скорость света в вакууме одна и та же для любой инерциальной системы отсчета. В первом постулате не было ничего нового, он использовался и в механике Ньютона, правда, Ньютон применял его к механическим явлениям, а Эйнштейн распространил абсолютно на все физические явления.
Но второй постулат был совершенно революционным. Макс Планк писал по этому поводу: «Теория относительности приписывает абсолютный смысл такой величине, которая в классической физике обладает лишь относительным характером, – скорости света». Преобразования Лоренца являлись прямым следствием этого постулата. Второй постулат Эйнштейна противоречил принципам классической механики, созданной Ньютоном: там использовался закон сложения скоростей. Но скорость света постоянна всегда, независимо от скорости источника, который излучает свет. Законы Ньютона на нее не распространяются.
Эйнштейн вывел постоянство скорости света путем математических расчетов, из формул Максвелла. Сочетание этой константы с принципом относительности давало совершенно новое представление о многих понятиях и законах физики.
Одним из важнейших и интереснейших выводов, следующих из постоянства скорости света, стало изменение понятия одновременности.
Если две инерциальные системы отсчета движутся относительно друг друга, то два события, происходящие одновременно в одной из систем отсчета, могут не быть одновременными в другой. Для того чтобы проиллюстрировать это положение, вернемся к примеру с кораблем и наблюдателем на причале, к которому прибегал Галилей.
Итак, первый наблюдатель находится на причале, второй – в трюме движущегося корабля. Если второй наблюдатель встанет в центр трюма и одновременно бросит в две стены, расположенные напротив друг друга, мячики, то они достигнут стен одновременно. (Представим, что скорость у этих мячей одинаковая.) Если при этом корабль движется слева направо, то для наблюдателя, стоящего на причале, эти события будут выглядеть так: мячу, летящему вправо, нужно преодолеть большее расстояние, при этом его скорость становится больше за счет сложения со скоростью корабля. Расстояние, которое нужно пролететь левому мячу, сокращается за счет движения корабля, но и скорость тоже уменьшается, так как из нее нужно вычесть скорость движения судна. Таким образом, мячи все равно ударятся о стены одновременно И для первого, и для второго наблюдателя ситуация выглядит одинаково Это механический эксперимент, в нем действуют законы Ньютона.
Теперь изменим условия эксперимента: вместо мячей будут действовать фонарики, посылающие световые лучи в противоположные стороны. Для второго наблюдателя, находящегося в трюме, ситуация будет аналогична предыдущему эксперименту: лучи достигнут противоположных стен одновременно. Но для первого наблюдателя, который неподвижен сам, но видит движение корабля, все будет выглядеть иначе. Скорость света постоянна, закон сложения скоростей в этом случае не работает. Поэтому луч, направленный вправо, достигнет стены позже, чем луч, идущий влево: корабль движется, расстояние для левого луча сократилось, а для правого увеличилось. Получается, что события, одновременные в системе отсчета второго наблюдателя, не одновременны в системе отсчета первого.
Хендрик Лоренц вывел уравнения, позволяющие сохранять величины при переходе из одной системы отсчета в другую, еще до того, как Эйнштейн создал специальную теорию относительности. Изучая следствия второго постулата своей теории – постоянства скорости света, Эйнштейн обнаружил, что преобразования Лоренца выводятся из него даже без обращения к уравнениям Максвелла. Когда-то Лоренц обнаружил, что его преобразования имеют странные «побочные эффекты»: сокращение длины движущегося тела и замедление времени в движущемся объекте. Он считал, что на сокращение длины влияет эфир, свойства которого еще не изучены и потому непонятны, а замедление времени называл «кажущимся», считая его условным.
Мнение Эйнштейна по этому вопросу было полностью противоположным. Ученый был уверен: все эти эффекты имеют место в реальности, их восприятие зависит от системы отсчета. Ракета, пролетающая мимо нас со скоростью, близкой к скорости света, в нашей системе отсчета имела бы меньшие размеры, чем та же ракета в состоянии покоя. Для наблюдателей, смотрящих на нас из ракеты, ситуация была бы точно такой же. Так как движение относительно, то наблюдатели считали бы себя покоящимися, а нас – проносящимися мимо со скоростью, близкой к скорости света. И мы для них, так же как ракета для нас, имели бы меньшие размеры.
То, что в движущейся системе отсчета (при очень высоких скоростях) время замедляется, хорошо иллюстрирует так называемый «парадокс близнецов». Этот мысленный эксперимент выглядит так: один из близнецов остается на Земле, другой летит на далекую планету в ракете, которая развивает скорость, близкую к скорости света. Допустим, по земным меркам полет длился два года. Но для близнеца, который находился в полете, время шло гораздо медленнее, у него прошло всего несколько дней. Так что по возвращении он оказывается моложе своего брата.
Запаздывание времени в движущейся системе отсчета, также как другие следствия постулатов теории относительности, были выведены Эйнштейном математически, с использованием преобразований Лоренца. В привычном нам мире все эти теории кажутся невероятными, но они реально действуют в мире высоких скоростей и неоднократно подтверждены современной экспериментальной наукой.
Назад: «Год чудес»: невероятные открытия молодого ученого
Дальше: О двойственной природе света: вклад Эйнштейна в квантовую теорию

