Книга: О том, чего мы не можем знать. Путешествие к рубежам знаний
Назад: 9
Дальше: Рубеж шестой: Виртуальный собеседник
10
Есть место, где время недвижимо. Капли дождя повисают в воздухе. Маятники часов замирают на мертвой точке. Собаки задирают морды с безгласным воем. Прохожие оцепеневают на пыльных улицах с вздернутой, как у марионетки, ногой. Запахи фиников, манго, кориандра, тмина взвесью стоят в воздухе.Алан Лайтман. Сон Эйнштейна
Мне нравится дизайн моих часов. Их циферблат – это простой коричневый квадрат, обрамленный круглым серебряным корпусом. Мне нравится симметричность их формы, и в то же время между квадратом и кругом существует некое напряжение. Часы у меня недорогие, и это хорошо – я часто теряю часы.
Предыдущие часы соскользнули с моей руки, когда я ходил на каяке по озеру рядом с ледником на горе Кука. Я пытался спасти свои часы, но вода была настолько обжигающе холодной, что я не мог опустить в нее руку дольше чем на пару секунд. Хотя отмерить эти секунды мне теперь было нечем. Часы ушли под воду, и их механизм, наверное, заржавел и замерз; ледяные воды, стекающие с горы Кука, лишили их способности измерять время.
Если бы я хотел, чтобы мои нынешние часы перестали тикать, их можно было бы уронить в одну из математических сингулярностей, открытых в уравнениях общей теории относительности Эйнштейна, – это остановило бы и самые прочные часы на свете. Но для исследования этих сингулярностей, известных под названием черных дыр, мне понадобился бы не каяк, а космический корабль.
Горизонты, за которые мы не можем заглянуть
Вселенная – такое интересное место, а не просто однородный слой материи, потому, что благодаря наличию гравитации одни атомы притягивают к себе другие. И, если все не приходит в состояние абсолютного равновесия, мы видим, как одни элементы материи движутся к другим элементам материи. Но самая интересная особенность гравитации состоит в том, что притяжение между частицами материи становится сильнее по мере того, как они приближаются друг к другу. Именно это притяжение приводит к возникновению звезд, подобных нашему Солнцу, но оно же создает и возможность более катастрофических событий в пространстве-времени.
Простейший атом, атом водорода, состоит из одного электрона и одного протона, удерживаемых вместе электромагнитным взаимодействием. Если взять два атома водорода, они будут притягиваться друг к другу силой гравитации. И, по мере того как атомы будут притягиваться все ближе и ближе друг к другу, они начнут сталкиваться. Если число атомов водорода увеличить, они будут сталкиваться все более энергично до тех пор, пока не перестанут отскакивать друг от друга и пока не возникнут условия, в которых станет возможен термоядерный синтез – и тогда у нас образуется звезда. Атомы водорода будут сливаться, образуя атомы гелия. В этом процессе выделяется энергия, рассеяние которой создает давление, направленное вовне. Именно от этой энергии зависит существование жизни на Земле. Звезда остается устойчивой и более не стремится коллапсировать, так как направленное вовнутрь гравитационное притяжение уравновешивается направленным вовне давлением энергии, выделяемой в реакции синтеза.
В какой-то момент весь водород будет использован. В некоторых звездах процесс синтеза продолжается и после этого: атомы гелия сливаются друг с другом, образуя другие элементы периодической системы. Многие из атомов, которые мы находим на Земле, – атомы железа, кислорода, даже углерода, необходимые для образования жизни, – образовались именно в этом непрерывном процессе слияния более легких атомов, происходящем в звездах. Но в конце концов звезда оказывается не в состоянии далее поддерживать синтез – все ее топливо уже израсходовано. И тогда гравитация снова одерживает верх, и по мере сжатия звезды в игру вступает квантовая физика. По мере того как мы заключаем частицы во все меньшее и меньшее пространство, мы все более и более точно можем определить их положение. Согласно принципу неопределенности Гейзенберга, такая определенность должна быть скомпенсирована все большей неопределенностью скоростей этих частиц. Направленное в противоположные стороны движение частиц, противодействующее гравитационному притяжению, приводит к существованию второго устойчивого состояния, известного под именем белого карлика.
Однако в 1930 г. индийский физик Субраманьян Чандрасекар понял, что не все тут так гладко. Пока Чандрасекар плыл на корабле из Индии в Англию, где он должен был приступить к работе в докторантуре в Кембридже, он осознал, что специальная теория относительности устанавливает предельную скорость, с которой могут двигаться такие частицы. Поэтому если масса звезды достаточно велика, то после достижения этого предела гравитация победит и звезда начнет стремительно сжиматься, образуя в пространстве область все увеличивающейся плотности. Из вычислений, которые он произвел на своем корабле, следовало, что такая судьба ждет любую звезду, масса которой превышает массу Солнца более чем в 1,4 раза. В результате такого катастрофического сжатия – коллапса – возникает сверхновая, в которой происходит образование тяжелых элементов, например золота и урана.
Пространство, окружающее такие точки высокой плотности, искривляется чрезвычайно сильно, настолько, что свет, заключенный внутри его, не может выбраться наружу. В качестве одной из иллюстраций, объясняющих, как может возникнуть такая ловушка, можно представить себе мяч, который подбрасывают в воздух. Если такой мяч бросить с поверхности Земли с достаточно большой скоростью, он сможет освободиться от гравитационного притяжения Земли. Скорость, с которой для этого нужно бросить мяч, называется скоростью убегания. Но представим себе, что масса Земли постоянно увеличивается. Тогда увеличивается и скорость, необходимая для преодоления гравитационного притяжения. Однако в какой-то момент масса Земли станет такой большой, что скорость убегания мяча должна будет превысить скорость света. Начиная с этого момента мяч оказывается в ловушке. Он не может улететь дальше некоторой точки, из которой Земля притянет его обратно.
Так обстояло дело в классической картине гравитации, существовавшей до Эйнштейна. В конце XVIII в. Лаплас и английский физик Джон Мичелл уже присматривались к идее о возможности уловления света массивными объектами. Однако из сделанного столетием позже открытия Майкельсона и Морли, которые выяснили, что свет в вакууме всегда распространяется с одной и той же скоростью, следовало, что свет ведет себя не так, как мяч. Гравитация не может замедлить свет, как предполагали Лаплас и Мичелл. Но если гравитация является результатом искривления пространства-времени в соответствии с концепцией Эйнштейна, то такое искривление может помешать распространению света. Согласно идее Эйнштейна, может существовать область пространства настолько искривленная, что даже свет (не имеющий массы, но тем не менее подверженный влиянию кривизны пространства) не сможет ее покинуть. Пространство искривлено там настолько, что свет не может пробиться наружу, но загибается в обратном направлении, внутрь области высокой плотности. В 1967 г. американский физик Джон Уилер нарек такие области причудливым именем «черных дыр». Ричарду Фейнману оно показалось непристойным: французское выражение trou noir вызывает совсем другие ассоциации. Однако название прижилось.
По мере удаления от центра сжавшейся звезды воздействие гравитации ослабляется. В результате возникает сферическая граница, в центре которой находится черная дыра, и такая сфера определяет рубеж невозврата: свет, находящийся за пределами этой сферы, может выйти наружу; но свет и любые другие объекты, попавшие внутрь такой границы, оказываются в ловушке, так как их скорость недостаточна для выхода за нее. Такую сферу называют горизонтом событий черной дыры, потому что наблюдатель, находящийся снаружи сферы, не может увидеть события, происходящие внутри ее.
Для того чтобы звезда сжалась до размера такой сферы, ее масса должна быть достаточно большой. Например, масса Земли слишком мала для образования черной дыры – для этого ей пришлось бы сжаться до сферы радиусом всего в 1 см. Солнце тоже недостаточно массивно: радиус его горизонта событий составлял бы всего 3 км. Но, если масса звезды превышает массу нашего Солнца в 1,4 раза, направленное вовнутрь гравитационное давление преодолевает любое порожденное импульсом заключенной в ней материи давление, направленное вовне, и такая звезда коллапсирует внутрь своего горизонта событий.
Черные дыры были предметом оживленных споров с тех самых пор, когда теоретическое предположение об их существовании было впервые высказано после публикации уравнений гравитации Эйнштейна в 1915 г. Некоторые считали, что сжимающиеся звезды могут каким-то образом избежать попадания в такие запретные области. Может быть, такая звезда отбросит лишнюю массу? Это, конечно, допустимо, но звезда, в 20 раз более тяжелая, чем Солнце, смогла бы избежать превращения в черную дыру, только отбросив 95 % своей массы, что не кажется вероятным. Тем не менее некоторые ученые считали, что такие области пространства-времени в реальности не существуют.
В 1964 г. в созвездии Лебедь был найден первый потенциальный пример именно такой области высокой плотности. Законченные к 1971 г. расчеты массы и плотности этого объекта, названного Лебедь Х-1, показали, что он должен быть черной дырой. Эти результаты убедили не всех. Более того, один известный ученый заключил в 1975 г. пари, в котором ставил на то, что Лебедь Х-1 – не черная дыра. Это был Стивен Хокинг. Такое пари выглядело несколько странно с учетом того, что сам он посвятил значительную часть своей исследовательской работы именно изучению природы черных дыр. Если бы Лебедь Х-1 действительно оказался первым примером черной дыры, это подтвердило бы все результаты теоретических размышлений Хокинга.
Как Хокинг объяснял впоследствии в «Краткой истории времени», это пари было своего рода страховкой. Ставка на поражение любимой команды в финале Кубка Англии по футболу позволяет выиграть при любом исходе: если команда проиграет, можно хотя бы выгадать материально. Если бы оказалось, что работа всей его жизни – изучение черных дыр – была пустой тратой времени, он, по крайней мере, выиграл бы пари. На что спорили? На подписку на журнал Private Eye, который должен был отвлечь Хокинга от огорчения по поводу провала его научной работы. Пари было заключено с другим космологом, Кипом Торном. В случае получения убедительных доказательств того, что Лебедь Х-1 действительно является черной дырой, Торн должен был получить подписку на любой журнал по своему выбору. Он выбрал Penthouse.
К 1990 г. накопилось большое количество свидетельств того, что Лебедь Х-1 действительно должен быть черной дырой: его масса оценивается в 14,8 массы Солнца, а размеры слишком компактны, чтобы он мог быть чем-нибудь другим. Полагают, что горизонт событий объекта Лебедь Х-1 составляет 44 км. Изнутри этой сферы, диаметр которой примерно равен расстоянию от Оксфорда до Кембриджа, не может выйти никакой свет. С учетом всех полученных данных Хокинг признал свое поражение. Торн получил подписку на Penthouse – к большому неудовольствию своей жены.
Однако в черных дырах есть нечто неправильное с точки зрения математики, нечто, вносящее свой вклад в сомнения в самой возможности их существования. Когда звезды сжимаются, образуя точки высокой плотности, по-видимому, не остается ничего противодействующего непрерывному стягивающему воздействию гравитации. Кажется, что они так и будут продолжать сжиматься, становясь все меньше и меньше, все плотнее и плотнее – и ничто не сможет остановить это схлопывание. Значит ли это, что коллапс звезды будет продолжаться, пока не образует единственную точку бесконечной плотности? Идея такой физической бесконечности была встречена очень неприязненно.
Абсурдность такого математического вывода пытался доказать сам Эйнштейн. Эддингтон видел, к каким следствиям приводит математика, но эти следствия ему активно не нравились: «Когда мы доказываем результат, не понимая его – когда он неожиданно появляется из лабиринта математических формул, – нет оснований надеяться, что мы сможем где-то его применить». Но в 1964 г. британский математик Роджер Пенроуз доказал, что такие сингулярные точки являются необходимым следствием общей теории относительности.
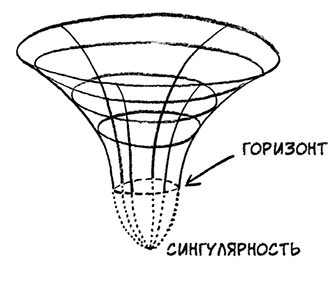
Черная дыра в двумерном пространстве-времени. Горизонт событий обозначен окружностью, изнутри которой мы не можем получить никакой информации
Работая в сотрудничестве с молодым Стивеном Хокингом, Пенроуз доказал, что такая же бесконечная плотность возникает при обратном просмотре истории Вселенной вплоть до Большого взрыва. И черные дыры, и Большой взрыв являются примерами математического объекта, называемого сингулярностью, в общей теории относительности. К сингулярностям относится целый ряд ситуаций, в которых невозможно установить, что происходит. Сингулярность есть точка, в которой наша способность моделировать сценарии развития событий перестает работать. Это то место, в котором мы вынуждены поднять руки и признать, что мы чего-то не знаем.
Сингулярности
Сингулярность – эта такая точка, в которой математическая функция перестает работать. Функция в математике подобна компьютерной программе. В нее вводят числа, функция их обсчитывает и выдает ответ. Математики часто представляют функции визуально, в виде графиков. Вводимые числа откладывают по горизонтальной оси, а результат изображают в виде кривой.
Рассмотрим, например, функцию, в которую вводят расстояние до массивного объекта, а в качестве результата получают величину гравитационного притяжения, порождаемого в данной точке этим массивным объектом. Ньютон осознал, что такое притяжение становится тем слабее, чем больше расстояние до объекта. Он открыл очень точное соотношение между величиной притяжения и расстоянием. Если я нахожусь на расстоянии х от планеты, то, согласно функции Ньютона, сила гравитационного притяжения пропорциональна 1/х2. Это так называемый закон обратных квадратов. Можно нарисовать график этой функции.
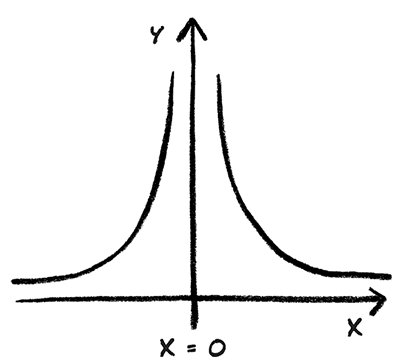
График функции 1/x2. Функция имеет сингулярность в точке x = 0
Однако при приближении к объекту происходит нечто интересное. Сила становится все больше и больше, пока мы не доходим до точки х = 0, в которой результат становится бесконечным, а на графике нельзя отложить значение. Разумеется, в реальности такое расстояние измеряется от центра планеты и при достижении ее поверхности функция и график изменяются, потому что после прохождения сквозь поверхность планеты разные ее части начинают оказывать притяжение в других направлениях. В центре тяжести планеты все разнонаправленные притяжения уравновешиваются и суммарное гравитационное притяжение равно нулю. Но что будет, если заменить планету на черную дыру, пространственную область, вся масса которой должна быть сосредоточена в единственной точке? Эта точка имеет бесконечную плотность, и при приближении к ней гравитационное притяжение становится бесконечным.
Тот факт, что данная функция не имеет смысла при х = 0, математики называют сингулярностью. Сингулярности бывают разные, но все они содержат точку, в которой функция не дает разумных результатов или имеет разрывный скачок от одного значения к другому.
Очень примитивный пример сингулярности можно получить, если взять монету и закрутить ее на столе. В отсутствие трения и сопротивления воздуха монета вечно продолжала бы вертеться с постоянной скоростью. Однако вследствие наличия рассеяния энергии монета вечно вертеться не будет. Вместо этого угол ее наклона к поверхности стола уменьшается, но, что интересно, пропорционально ему увеличивается скорость ее вращения. По мере приближения угла к нулю скорость в конце концов становится бесконечной. На последних стадиях вращения монета падает на стол, вибрируя и издавая жужжащий звук, частота которого быстро увеличивается, пока наконец дрожащая монета не останавливается.
Уравнения движения показывают, что скорость вращения монеты возрастает так, что через конечное количество времени она достигает бесконечного значения. Именно этот эффект мы слышим, когда увеличивается частота звука. Вертящаяся монета дает нам пример сингулярности. Разумеется, при этом действуют и другие эффекты, которые не допускают полного осуществления такой математической бесконечности, но этот пример показывает, что для получения бесконечности из физического уравнения не обязательно бросаться в черную дыру.
Даже Ньютоновы уравнения планетарного движения могут порождать сингулярности. Как я объяснял в конце первого «рубежа», математик Ся Чжихун показал, что четыре планеты можно расположить таким образом, что пятая планета будет вытолкнута из их среды и наберет бесконечную скорость за конечное время. Уравнения ничего не говорят о дальнейшей судьбе такой планеты, ожидающей ее после этой астрономической сингулярности.
Сингулярности обычно соответствуют моментам, в которые в игру вступает бесконечность и развитие событий после которых предсказать невозможно. Такие сингулярности могут возникать не только в физике. Известен пример статьи, которую опубликовали в 1960 г. Хайнц фон Фёрстер, Патриция Мора и Лоуренс Амиот, предсказывая серьезную сингулярность, которая должна произойти здесь, на Земле. Если скорость роста населения и дальше будет следовать закономерностям, наблюдавшимся до 1960 г., то население нашей планеты должно стать бесконечным 13 ноября 2026 г. Особо отметим для суеверных, что этот день выпадет на пятницу.
Простейшая модель роста популяции утверждает, что этот рост имеет экспоненциальный характер. Например, численность некоторого вида может удваиваться каждые 50 лет. В такой модели популяция быстро разрастается, но никогда не становится бесконечной. Но анализ исторических данных, проведенный авторами этой статьи, говорил о том, что период удвоения численности человечества становится все короче и короче.
Когда-то удвоение численности населения Земли заняло 1650 лет, с 250 миллионов в нулевом году нашей эры до 500 миллионов в 1650-м. До миллиарда эта численность дошла за следующие 200 лет, к 1850 г. Следующее удвоение заняло всего 80 лет. Всего через 44 года после этого, в 1974 г., население планеты достигло четырех миллиардов. Скорость роста превышала экспоненциальную. Поэтому на основе данных, имевшихся к 1960 г., авторы статьи оценили, что население Земли должно достичь сингулярности приблизительно через десятилетие после нынешнего момента.
Другой пример такого суперэкспоненциального роста можно найти в скорости увеличения вычислительной мощности компьютеров. Существует утверждение, называемое законом Мура, согласно которому производительность компьютеров удваивается каждые 18 месяцев. С такой скоростью роста компьютеры становятся все мощнее, но никогда не достигнут сингулярности. Однако высказывались и другие предположения: что сокращение периода удвоения населения справедливо также и для технологий. Возможность технологической сингулярности послужила основой так называемого движения сингулярианства. Его идеи были популяризованы изобретателем и футурологом Рэем Курцвейлом в книге «Сингулярность уже близка» (The Singularity Is Near), согласно которой человечество должно достичь сингулярности в 2045 г. Курцвейл считает, что к этому моменту человечество сумеет создать искусственный разум, превосходящий наш собственный. В этот же момент исчезнет наша способность предсказывать, как будет выглядеть жизнь после такой сингулярности.
Математическим уравнениям следует доверять с осторожностью, потому что может существовать какой-то скрытый элемент, который становится важным только при приближении к сингулярности и играет неожиданно важную роль в предотвращении физической реализации такой бесконечности. Это явно происходит в случае роста численности человечества: конечность поверхности Земли создает предел, который рано или поздно ограничит численность населения.
Сходные факторы могут действовать и в случае Большого взрыва и черных дыр. Кое-кто предполагает, что уравнения общей теории относительности неприменимы к таким экстремальным условиям. Например, в уравнения гравитации Эйнштейна, возможно, следует ввести еще один член, который вступает в действие только при приближении к сингулярности. Это изменит и происходящее при приближении к сингулярности Большого взрыва, но такой дополнительный элемент останется практически незаметным, пока дело не дойдет до действительно экстремальной ситуации. Он подобен тем тонким изменениям, которые Эйнштейну пришлось внести при рассмотрении движения с околосветовой скоростью: на малых скоростях дело ограничивается простым прибавлением скорости, но, как понял Эйнштейн, при приближении к скорости света необходимо действовать с большей осторожностью. Как я объяснял в предыдущей главе, формула скорости человека, бегущего вдоль движущегося поезда относительно платформы, дается сложением скоростей человека и поезда, но затем ее нужно разделить на вторую формулу. На малых скоростях значение этой второй формулы настолько близко к единице, что эффект такого деления пренебрежимо мал, – именно поэтому до Эйнштейна ученые считали, что скорости просто складываются. Но вблизи скорости света определяющим становится другая закономерность. То же может быть справедливо и в отношении Большого взрыва или черной дыры. Уравнениям общей теории относительности может быть необходим дополнительный член, оказывающий заметное действие только в случаях экстремально сильной гравитации.
Но, если Вселенная все-таки содержит сингулярные точки бесконечной плотности, как они могут влиять на время? Эйнштейн выяснил, что увеличение гравитации замедляет время. Что же произойдет с моими часами, если я приближусь к такой сингулярной точке предельно высокой гравитации?
Неизвестное, скрывающееся внутри черной дыры
Если бросить мои часы в черную дыру, произойдет нечто странное. Оставаясь на Земле и наблюдая, как часы падают в черную дыру, можно заметить момент, в который время, по-видимому, останавливается. Ход часов все более и более замедляется, пока не прекращается вовсе. В конце концов видимое изображение часов замерзает, а затем постепенно бледнеет и исчезает. Горизонт событий, окружающий черную дыру, подобен пространственному пузырю, за которым время, похоже, больше не работает. Оно не может продолжать свой ход. Наблюдателю, находящемуся вне черной дыры, кажется, что у времени в ней не существует «после». Может ли эта картина быть обратной тому, что происходит со временем при возвращении к Большому взрыву? Там у времени не существует «до».
Но не будем забывать, что все это – с точки зрения наблюдателя, сравнивающего течение времени на Земле с тем, что он видит на моих часах, направляющихся к черной дыре. А как все это будет выглядеть, если я сам отправлюсь к такой математической сингулярности с часами на руке? Мои впечатления будут совершенно иными. С Земли представлялось, что часы останавливаются, когда достигают горизонта событий черной дыры. Но теперь, когда я сам пересекаю горизонт событий, мне кажется, что часы преспокойно продолжают тикать. Более того, я даже не смогу заметить момента пересечения этой линии невозврата.
Это не значит, что при падении в направлении черной дыры со мной все будет в порядке – с тем, что происходит с пространством-временем при приближении к этому бесконечно плотному центру, так просто не разделаешься. Если я буду лететь к центру черной дыры ногами вперед, гравитация будет воздействовать на мои ноги сильнее, чем на голову, растягивая меня в некое подобие макаронины. В течение конечного времени все, включая мои часы, окажется сжато в сингулярность, и время закончится. Подобно прямой, прочерченной на листе бумаги, время достигнет края, и продолжать его станет некуда.
Странно, что во всех других местах время продолжает идти как ни в чем не бывало. Подобная судьба, видимо, ожидает всех нас. Когда мы умираем, для нас время останавливается, но мы знаем, что для других оно по-прежнему продолжает идти. Я не могу ощутить собственную смерть – и точно так же я не смог бы ощутить достижение пространственно-временной сингулярности.
Мой друг физик дал мне полезный совет на случай падения в черную дыру: как и в случае зыбучих песков, лучше всего не сопротивляться. В свободном падении навстречу неизбежному можно прожить дольше. Кажется, что это противоречит здравому смыслу. Но друг напомнил мне о том, что происходит с часами под действием гравитации и ускорения. Если я буду сопротивляться и пытаться создать ускорение, направленное от черной дыры, окажется, что там, где я нахожусь, время замедляется. Увеличенное ускорение, как и гравитация, замедляет время. И в результате я быстрее попаду в будущее окружающего меня пространства-времени – как моя улетавшая с ускорением дочь Ина попала в будущее своей сестры-близнеца Магали. Поэтому, если я буду сопротивляться, приближаясь к сингулярности, я состарюсь меньше. Но радости от этого будет немного: я просто исчезну в сингулярности, прожив более короткую жизнь. Поэтому лучше всего не сопротивляться, чтобы до попадания в сингулярность осталось как можно больше времени.
Самое интересное, что наблюдатель, находящийся за пределами горизонта событий, никогда не узнает, что происходит внутри его. С его точки зрения, время останавливается, как только я пересекаю горизонт событий, и узнать, что случится потом, невозможно – хотя для меня, растягивающегося в макаронину, такое «потом» существует. Поэтому вопрос о том, что происходит после, не кажется лишенным смысла. Проблема только в том, что законы физики не позволяют получить ответ на него никому, находящемуся вне горизонта событий.
Было высказано предположение, что тот же принцип применим и к проблеме знания того, что происходило до Большого взрыва – если до него вообще что-нибудь происходило. Внутри черной дыры время заканчивается. Но Большой взрыв подобен коллапсу звезды в черную дыру, проигранному задом наперед. Поэтому можно предположить, что при приближении к Большому взрыву время также заканчивается. Другими словами, можно заключить, что у времени есть начало, что само время началось с Большого взрыва.
Сингулярности пространства-времени – это края, точки, в которых мы упираемся в тупик, не пускающий нас дальше. Понять такие края пространства-времени трудно: даже если нам нельзя двигаться дальше, за таким краем все же может существовать что-то еще.
Черные дыры не только ставят под сомнение наше понимание времени, но и, по-видимому, противоречат одному из других открытий современной физики – принципу, согласно которому информация не может быть утрачена.
Абсолютный шредер
У законов квантовой физики есть одно довольно замечательное следствие: они обратимы. Это означает, что информация никогда не может быть утрачена. Такое положение вещей в сильной степени противоречит здравому смыслу. Например, если я подпишусь на журналы Private Eye и Penthouse, а потом сожгу годовые комплекты их обоих, то, казалось бы, невозможно будет определить, какому журналу соответствует та или другая кучка пепла.
Но если иметь полную информацию обо всех атомах и фотонах, содержащихся в таком костре, то теоретически можно запустить процесс сгорания в обратную сторону и восстановить информацию, содержавшуюся в журналах. На практике это, разумеется, было бы чрезвычайно сложно, но наука утверждает, что в этом процессе нет ничего необратимого. Законы физики работают в обе стороны.
Существование черных дыр ставит эту идею под сомнение. Если бросить один из журналов в одну черную дыру, а другой – в другую черную дыру, невозможно будет установить, в какую из черных дыр попал тот или другой журнал. Черные дыры кажутся абсолютным шредером, в котором информация действительно может быть утрачена навсегда.
Черные дыры представляют особенный интерес с точки зрения моих поисков того, чего мы знать не можем, потому что, когда что-нибудь исчезает внутри горизонта событий – границы, за которую не может выйти свет, – информация о том, что пересекло такой горизонт, судя по всему, утрачивается. Если я возьму игральную кость, которая сопровождает меня в поисках того, чего мы не можем знать, и брошу ее в черную дыру, то после того, как она пересечет горизонт событий, я, по-видимому, не смогу узнать, какой стороной она там упадет. С той стороны может стоять стол, на котором на этой кости выпадет шестерка. Некто, находящийся по ту сторону горизонта событий, может увидеть этот результат, но никогда не сможет сообщить о нем, так как все находящееся там заключено в ловушку.
Согласно общей теории относительности, наблюдая черную дыру извне, можно узнать лишь ее массу, угловой момент и электрический заряд. Вся прочая информация утрачена. Эта ситуация известна под ироническим названием «теоремы об отсутствии волос» – считается, что любая другая информация была бы подобна волосам на гладком круглом шаре, представляющем черную дыру. Я могу бросить в черную дыру свою игральную кость, свою виолончель, свои часы, и, как только они пересекут горизонт событий, ничто из внешних свойств такой черной дыры не будет говорить о том, что в нее бросили. Обратить события вспять, чтобы узнать, что именно пересекло горизонт событий, невозможно.
Несмотря на ее название, теорему об отсутствии волос скорее следовало бы считать гипотезой, поскольку неопровержимых доказательств того, что информация действительно утрачивается, нет. Более того, в 1974 г. возникли сомнения в том, насколько горизонт событий скрывает то, что происходит внутри черной дыры. Это связано с тем, что, если верить Стивену Хокингу, черные дыры испаряются.
Не такие уж и черные черные дыры
Бросив игральную кость в черную дыру, по-видимому, невозможно узнать, какой стороной она упадет. По крайней мере, многие полагали, что именно таким должно быть следствие такой концентрации искривленного массой пространства-времени. Но, когда Хокинг применил к черным дырам второе начало термодинамики, оказалось, что эти дыры не столь черны, как предполагалось изначально.
Второе начало термодинамики утверждает, что мы движемся от высокоупорядоченной Вселенной ко Вселенной, содержащей беспорядок. При этом изменяется величина, называемая энтропией системы. Энтропия есть мера беспорядка. По существу, она определяет число различных возможных сценариев реализации данного состояния и тем самым оказывается мерой его вероятности. И второе начало термодинамики гласит, что энтропия Вселенной возрастает.
Вот классический пример увеличения энтропии: рассмотрим газ, заключенный внутри сосуда. Если весь газ сконцентрирован в одном из углов сосуда (предположим, он был сжат внутренними стенками, которые потом убрали), то он со временем распространится по всему его объему. Энтропия определяет число возможных сценариев реализации такого распределения газа. Пока газ заключен в одном из углов, число таких сценариев меньше, чем после исчезновения стенок и распространения газа по всему сосуду. Энтропия возрастает с ростом числа возможных сценариев. Вначале энтропия мала, но впоследствии она увеличивается.
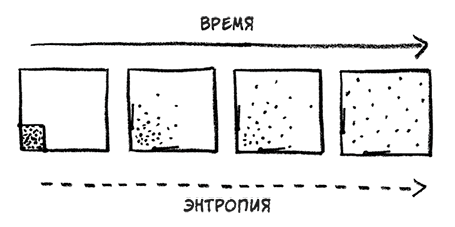
Также можно рассмотреть бытовой пример яйца, которое падает со стола и разбивается об пол. Высокоупорядоченное яйцо превращается в разбросанную массу осколков скорлупы. Разбитую скорлупу можно расположить множеством разных способов, помимо единственного исходного состояния, в котором целая скорлупа окружала яйцо. Если посмотреть видеозапись этого события, проигранную в прямом и обратном направлении, совершенно очевидно, какой из вариантов соответствует реальному течению времени. Увеличение энтропии определяет направление оси времени.
Именно поэтому энтропия тесно связана с понятием времени. Это одна из немногих вещей, которые помогают нам понять, в какую сторону следует крутить это кино. Многие другие физические законы превосходно работают как в прямом, так и в обратном направлении. Хотя физическая возможность восстановления целого яйца на столе и существует, связанное с ней уменьшение энтропии показывает, как мала вероятность такого события.
Однако возникает интересный вопрос: откуда взялся тот исходный порядок, который существовал в яйце изначально? Может показаться, что такое движение от порядка к беспорядку на Земле не проявляется. Мы сами развились из беспорядка доисторических болот и достигли состояния, в котором у нас есть жизнь, яйца и порядок. Но это кажущееся нарушение второго начала термодинамики можно разрешить, потому что Земля получает низкую энтропию из другого источника – речь идет об обмене. Фотоны, прилетающие от Солнца и являющиеся источником жизни на Земле, имеют низкую энтропию. Но Земля под их воздействием не нагревается, а испускает тепло в форме электромагнитных волн более низкой частоты (и, следовательно, энергии), причем число таких волн увеличивается.
Таким образом, небольшое число высокоэнергетических волн Солнца превращается в большее число волн более низкой энергии, испускаемых Землей. Увеличение числа лучей означает увеличение числа возможных сценариев их испускания. Этот процесс чем-то похож на разбивание яйца. Единственный высокочастотный фотон поглощается Землей подобно яйцу, падающему на пол, а затем Земля разбрасывает множество низкоэнергетических фотонов, как осколки яичной скорлупы. При этом Земля получает уменьшение своей суммарной энтропии, и мы наблюдаем возникновение порядка из хаоса. Но в масштабах общей системы Земли и Солнца энтропия увеличивается в полном соответствии со вторым началом термодинамики.
Что же случится с сосудом, заполненным газом, если его бросить в черную дыру? Или, что еще интереснее, что случится с его энтропией? Считается, что, находясь вне горизонта событий, мы утрачиваем любую информацию о происходящем внутри его. Теряется ли там энтропия, что привело бы к уменьшению энтропии, противоречащему второму началу термодинамики? Может быть, следует считать, что черная дыра обладает собственной энтропией, которая возрастает по мере попадания в нее разных объектов? Но, поскольку мы не имеем никакого представления о том, что происходит внутри черной дыры, было сделано предположение, что ее энтропия может быть пропорциональна площади поверхности сферы горизонта событий, которую мы можем вычислить. Ну хорошо, но физика утверждает, что все, что имеет энтропию, имеет и температуру, а все, что имеет температуру, излучает тепло. Получается, что черная дыра должна была бы испускать излучение, мощность которого обратно пропорциональна квадрату массы, заключенной внутри этой черной дыры. Но, если бы черные дыры излучали, они не были бы такими черными, как предполагает их название, а мягко светились бы в ночном небе.
Размытые края
Бессмыслица какая-то. Как черная дыра может что-то излучать, если все, включая свет, должно быть заперто внутри ее? Казалось, что для такого процесса просто не может существовать механизма. Так было, пока Хокинг не пустил в ход квантовую физику. Согласно принципу неопределенности Гейзенберга, горизонт событий должен быть несколько более размытым, чем следует из математических выводов общей теории относительности. Как мы видели на третьем «рубеже», из принципа неопределенности следует, что одновременное точное определение положения и импульса невозможно. Время и энергия также связаны между собой таким образом, что одновременно знать обе эти величины нельзя. Поэтому невозможен идеальный вакуум, в котором все величины равны нулю. Если бы все было равно нулю, все можно было бы точно знать.
В вакууме происходят квантовые флуктуации, в которых, например, может возникнуть пара, состоящая из частицы и античастицы: одна из них имеет положительную энергию, а другая – отрицательную. Возможно, именно этот механизм возникновения чего-то из ничего и запустил развитие Вселенной. Обычно частица и античастица, возникшие в космическом вакууме, быстро аннигилируют. Но если такая пара возникнет так, что частица с положительной энергией будет находиться вне горизонта событий черной дыры, а частица с отрицательной энергией будет заперта внутри его, то может произойти нечто интересное.
Мы получаем довольно странный эффект: внутренняя частица затягивается в черную дыру и, поскольку ее энергия отрицательна, уменьшает массу такой черной дыры, а частица с положительной энергией выглядит так, будто она была испущена из черной дыры. Черная дыра действительно светится – у нее есть температура, как и следовало ожидать в предположении, что черная дыра имеет положительную энтропию.
Минуточку. Но ведь в половине случаев частица с положительной энергией будет оказываться внутри черной дыры, а не вне ее. Разве это не приведет к увеличению массы черной дыры? Чтобы разрешить это противоречие, нужно учесть, что частица с отрицательной энергией, образовавшаяся за пределами горизонта событий, не имеет энергии, необходимой ей, чтобы улететь прочь, поэтому суммарный эффект таких случайных флуктуаций состоит в уменьшении общей массы черной дыры с течением времени.
Испускание так называемого излучения Хокинга пока не было обнаружено ни в одной из черных дыр, которые нам до сих пор удалось распознать. Проблема состоит в том, что, согласно математическим выкладкам, его интенсивность тем меньше, чем больше масса черной дыры. Поэтому черная дыра, масса которой равна нескольким солнечным, должна испускать его с такой низкой интенсивностью, что это излучение будет иметь меньшую температуру, чем реликтовое излучение. Это означает, что мы не можем выделить его из фоновых шумов, оставшихся от Большого взрыва.
Поразительное следствие гипотезы Хокинга состоит в том, что она предлагает возможный механизм исчезновения черных дыр, масса которых уменьшается с течением времени. По мере уменьшения массы интенсивность излучения возрастает, и в конце концов, как полагают, черная дыра может исчезнуть с резким хлопком. По мнению Хокинга, такой хлопок может быть довольно сильным – сравнимым со взрывом миллионов водородных бомб. Однако другие исследователи считают, что он скорее должен быть сравним по силе со взрывом артиллерийского снаряда.
Тем не менее при этом мы получаем новую загадку. Куда девается информация, попавшая в черную дыру? Я могу согласиться, что информация может быть заперта внутри черной дыры – по крайней мере, она все еще существует. Но, если черная дыра в конце концов исчезает, исчезает ли информация вместе с ней? Или же она каким-то образом оказывается закодирована в излучении, выходящем из этой сингулярности? Можно ли, бросив игральную кость в черную дыру, каким-то образом узнать, какой стороной она упала, по частицам, испускаемым с края горизонта событий? Возможно, как и в случае с сожженными журналами, существует некий теоретический способ проанализировать такое излучение и извлечь из него информацию обо всем, что исчезло за горизонтом событий? Загадку о том, что происходит с такой информацией, называют информационным парадоксом черных дыр.
В 1997 г. Хокинг заключил еще одно пари, и на этот раз Кип Торн был на его стороне. Они поспорили с физиком из Калтеха Джоном Прескиллом. Они считали, что такая потеря информации неизбежна. Но, поскольку она противоречит квантовой теории, Прескилл не был готов примириться с возможностью утраты информации. На этот раз ставкой была не подписка на журналы, а энциклопедия по выбору победителя. Энциклопедия должна была символизировать вопрос о том, что произойдет с информацией, содержащейся в энциклопедии, которую бросили в черную дыру: может ли она быть как-то закодирована во вновь возникающих частицах, излучаемых в соответствии с принципом неопределенности?
В 2004 г. Хокинг торжественно признал свое поражение. Прескилл получил книгу «Все о бейсболе». Хокинг впоследствии шутил: «Я отдал Джону бейсбольную энциклопедию, но, может быть, надо было просто отдать ему пепел».
Теперь Хокинг полагает, что попадающая в черную дыру информация кодируется на поверхности горизонта событий, заключающего в себе такую черную дыру, и передается испускаемым с нее частицам. Как ни странно, эта двумерная поверхность, по-видимому, кодирует информацию о находящемся внутри ее трехмерном пространстве. Отсюда возникла идея голографической Вселенной: вся наша трехмерная Вселенная – всего лишь проекция информации, содержащейся на двумерной поверхности. Хотя Хокинг и признал свое поражение в споре, Торн по-прежнему отстаивает свою позицию. Он все еще считает, что информация утрачивается.
Роджер Пенроуз, как и Торн, полагает, что Хокинг сдался раньше времени. Пенроуз полагает, что при исчезновении черной дыры в результате излучения информация и энтропия утрачиваются. По мнению Пенроуза, это имеет отношение к вопросу о причинах столь низкой энтропии Вселенной в начале ее развития. Существовал ли изначальный порядок, благодаря которому вообще возникло второе начало термодинамики? Откуда взялся этот порядок? Если черные дыры действительно уничтожают энтропию, они могут содержать механизм, позволяющий вернуть Вселенную в низкоэнтропийное состояние.
Пенроуз также считал, что Большой взрыв является границей, за которой физика невозможна. По мере приближения к сингулярности Большого взрыва законы физики перестают работать. Если мы согласимся с определением Большого взрыва как точки бесконечной плотности, то вопрос о том, что было до Большого взрыва, во многих отношениях не будет иметь смысла: по ту сторону такой сингулярности физические законы могут быть какими угодно. Измерение чего бы то ни было, находящегося за этой сингулярностью, также невозможно, так что мы с тем же успехом можем считать, что за ней ничего нет. Или не можем? Пенроуз, например, передумал.
Смычка прошлого и будущего
Существуют разные истории о том, что могло происходить до Большого взрыва, и одну из самых удивительных таких историй рассказывает Пенроуз. Он предполагает, что наш Большой взрыв был всего лишь одним в бесконечном цикле больших взрывов. Такая идея высказывалась и раньше: когда предполагали, что Вселенная окончится «Большим сжатием», казалось логичным считать, что такое сжатие станет «Большим взрывом новой эры».
Но, как мы выяснили на четвертом «рубеже», Вселенная не сжимается, а расширяется со все увеличивающейся скоростью, стремясь к холодному состоянию, в котором не будет ни жизни, ни галактик, ни даже вещества – только световые фотоны. Пенроуз называет это состояние «очень скучной эрой». Поскольку считается, что даже черные дыры, которые поглотят большинство видимых сейчас галактик, испускают излучение, то и они тоже закончатся, исчезнут с прощальным хлопком и оставят после себя Вселенную, полную фотонов и гравитонов, гипотетических безмассовых частиц, которые считают переносчиками гравитационного взаимодействия.
Пенроуз признавал, что такое видение будущего Вселенной его несколько угнетало: «Боже мой, неужели нас ждет именно это!» Но потом ему в голову пришел вопрос о том, кто сможет наблюдать это состояние «всепоглощающей финальной скуки». Уж точно не мы. Скучать придется только тем же фотонам и гравитонам, которые одни и останутся во Вселенной.
Но фотон, как выясняется, не имеет понятия о времени. Он существует в безвременной среде. Теория относительности утверждает, что при приближении к скорости света время замедляется, так что при ее достижении часы и вовсе останавливаются. Но погодите. Свет распространяется со скоростью света. Это значит, что для фотона время не существует. Более того, в сценарии Пенроуза, в котором все массивные частицы должны распасться на безмассовые фотоны или гравитоны, не остается вообще ничего, что могло бы отмечать течение времени, ничего, из чего можно было бы сделать часы. Точно так же, поскольку время необходимо для измерения пространства, в такой будущей Вселенной исчезнет и всякая возможность исчисления и измерения расстояний – понятия большого и малого утратят смысл.
Вместо того чтобы поддаться пессимизму, Пенроуз увидел в этой картине новые возможности. Не правда ли, все это чрезвычайно похоже на состояние Вселенной сразу после Большого взрыва? Вселенная, полная энергии, в которой еще не сформировалось никакой материи. Конечно, для образования условий Большого взрыва такая энергия должна была быть сконцентрирована в бесконечно малой области. Но если во Вселенной исчезли все масштабы, то не могут ли условия такого конца нашей Вселенной быть отправной точкой нового Большого взрыва, порождающего вселенную, которая заново установит масштабы и сконцентрирует энергию для нового начала?
На самом деле эти два сценария – Вселенная, заканчивающая свое существование скучной тепловой смертью, и Вселенная, начинающаяся с захватывающего Большого взрыва, – можно элегантно объединить в один, подобно двум пейзажам с совпадающими краями, которые образуют один общий пейзаж. Для сшивания этих сценариев нужно, чтобы в конце одной Вселенной происходило сжатие, а в начале следующей – расширение, так, чтобы они могли быть соединены и плавно перетекали друг в друга. Холодные и далеко разбросанные фотоны становятся фотонами горячими и тесно сгруппированными, которые и запускают новый Большой взрыв.
Теория Пенроуза небесспорна, и мне не удалось найти много ученых, которые видели бы в ней нечто большее, чем хитроумную математическую идею. И все же, когда Пенроуз впервые показал, что математика общей теории относительности предсказывает существование в пространстве-времени сингулярностей, эта идея также была отвергнута многими как физически невозможная. Его нынешняя теория временных циклов может оказаться ошибочной, но мне кажется замечательным случай ученого, который меняет свою точку зрения на возможность исследования времени до Большого взрыва.
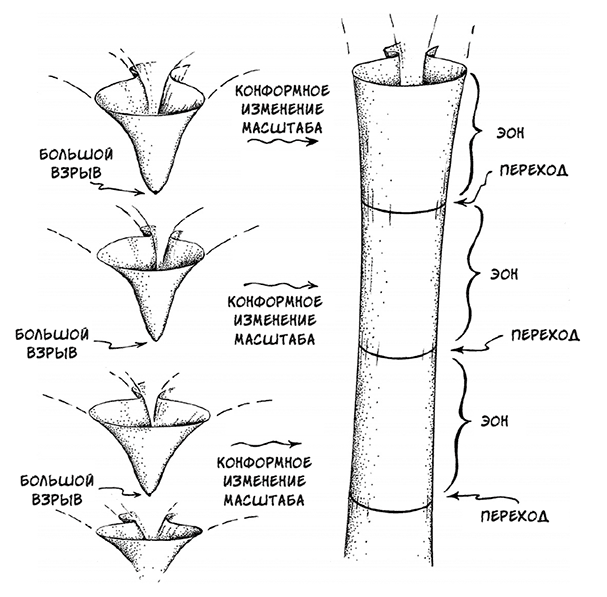
Изменение масштаба Вселенной в конце одного эона к началу следующего позволяет плавно переходить от эона к эону
Пенроуз называет период между двумя большими взрывами эоном, и наш эон – лишь один из, возможно, бесконечного множества эонов, предшествовавших нашему и следующих за ним.
Одна из наиболее существенных проблем этой модели, как и многих других циклических моделей, связана со вторым началом термодинамики. Как энтропия возвращается на такой низкий уровень, что второе начало термодинамики может заново начинать работать в каждом следующем эоне?
Сингулярность Большого взрыва есть состояние чрезвычайно низкой энтропии. По мере эволюции Вселенной энтропия возрастает – как можно обеспечить гладкий переход в новый эон со сбросом накопленной энтропии? Именно поэтому Пенроузу не понравилось, что Хокинг признал свое поражение в пари о черных дырах. С точки зрения Пенроуза, черные дыры представляют собой механизм снижения энтропии. Вся энтропия, попадающая в черную дыру, утрачивается или вычитается из системы, так что к концу эона мы снова имеем низкую энтропию, потому что вся информация уже утрачена во множестве черных дыр, населяющих Вселенную. Таким образом и устанавливаются условия, необходимые для следующего Большого взрыва.
Даже если эта теория справедлива, как мы можем добраться до периода, предшествовавшего нашему собственному Большому взрыву, чтобы проверить ее или другие теории на этот счет? Остается ли период «до Большого взрыва» запретной зоной? Пенроуз так не думает. Раз совмещаемые пейзажи должны соответствовать друг другу, события предыдущего эона должны оказывать влияние на наш. Пенроуз считает, что столкновения черных дыр на заключительных этапах предыдущего эона должны были создать гравитационную рябь, которая перешла в наш эон. Он приводит в пример картину пруда, в который бросили множество камешков. После того как черные дыры – или камешки – исчезают из виду, на пруду остается узор из ряби, образованный при взаимодействии кругов, расходящихся от этих камешков.
Пенроуз полагает, что такую рябь можно искать в реликтовом излучении – излучении, оставшемся после Большого взрыва, с которого началась наша Вселенная. Хотя флуктуации этого излучения кажутся случайными, возможно, некоторые из них появились в результате столкновений черных дыр, происходивших в конце предыдущего эона.
Проблема состоит в том, что анализировать реликтовое излучение исключительно трудно – в частности, потому что его очень мало. Это может показаться чрезвычайно странным, учитывая, что оно образует поверхность сферы, охватывающей всю наблюдаемую Вселенную. И тем не менее, если пытаться изучать участки этой сферы, окружающей Вселенную, и взять, скажем, сектор этой сферы размером в 10°, то еще не рассмотренные объекты очень быстро заканчиваются. Хотя многие сомневаются в том, что свидетельства существования предыдущих эонов можно найти в нашем собственном эоне, сама мысль о такой возможности открывает весьма захватывающие перспективы. Может быть, ответ на вопрос о том, что происходило до Большого взрыва, все-таки не настолько невозможен, как нам казалось!
Галилей нашего времени
Я зашел к Пенроузу, оксфордский кабинет которого расположен этажом ниже моего, чтобы узнать, что он думает о возможности познания происходившего до Большого взрыва. Пенроузу сейчас за восемьдесят, и он являет собой прекрасный пример неутолимой жажды знаний. Исходя из того, что он когда-то написал книгу с подзаголовком «Законы, управляющие Вселенной. Полный путеводитель», можно было бы предположить, что, по его мнению, он знает все. Но Пенроуз продолжает задавать все новые и новые вопросы.
– Когда-то я утверждал, что Большой взрыв был сингулярностью, а потому понятие времени до Большого взрыва не имеет смысла. «До» – бессмысленное понятие. Перестаньте задавать этот вопрос. Я слышал, как Стивен Хокинг просил его не задавать, и я был с ним согласен. Но теперь я считаю, что на самом деле этот вопрос задавать можно.
Значит ли это, что Пенроуз думает, что не было вообще никакого начала?
– Я думаю, что есть бесконечная последовательность эонов.
Я спросил его, можно ли считать эту тему примером того, чего мы знать не можем. В конце концов, бесконечность обычно считается в физике запретной зоной.
– Возможно, мы сумеем усовершенствовать свои технологии и заглянуть на несколько эонов назад. Но вернуться к самому началу всех эонов? Ну, это вполне кандидат на роль непознаваемого. Говорят, что бесконечность непознаваема, но математики все время ее используют. И чувствуют себя совершенно как дома. Ну, не совершенно, но почти.
Когда я спросил Пенроуза, существуют ли, по его мнению, вопросы, на которые невозможно ответить по самой их природе, он дал типично осторожный ответ.
«Идея о том, что может существовать что-то, что навсегда останется недосягаемым для нашего познания, меня несколько тревожит. Наверное, могут существовать вопросы, на которые не ожидаешь получить ответа. Задачи, которые кажутся неразрешимыми, – но потом мы придумываем, как их обойти, какие-то способы с ними разобраться. Мне не нравится слово “непознаваемый”. Оно просто означает, что мы неправильно на что-то смотрим.
Кто бы мог подумать, что мы узнаем, что происходит в центре Солнца? – и тем не менее сейчас известно, что там делается. Надо думать, еще не так давно этот вопрос считался бы неразрешимым.
Можно ли перемножить два невероятно больших числа так, чтобы результат содержал больше знаков, чем во Вселенной существует частиц, и потому его нельзя было бы записать? Можно ли считать эту задачу неразрешимой? По-моему, это очень скучная неразрешимая задача.
Мне кажется, что мне больше нравится (хотя я не могу сказать, что это у меня такая осознанная позиция), мне больше по душе идея, что абсолютно непознаваемых вещей не существует. – Тут Пенроуз несколько забеспокоился. – Надеюсь, я вас не разочаровал заявлением о том, что ничего непознаваемого нет».
Я предположил, что такой настрой может быть важен для занятий наукой.
– Задача может быть очень трудной, но при этом как-то чувствуешь, что у нее должно быть решение. У меня есть это чувство, но я не знаю, насколько оно обоснованно. Я не думаю, что узнаю ответы на все великие вопросы при жизни, но было бы неплохо увидеть решение некоторых наиболее насущных задач.
Я спросил, решение какой задачи он хотел бы узнать, если бы можно было выбрать одну из них. Поскольку Пенроуз много думает о времени, он выбрал вопрос о времени до Большого взрыва.
– Я хотел бы увидеть сигналы из предыдущего эона. Но нам пока до этого далеко.
Представляет ли избавление от необходимости начала угрозу для тех, кто верит в Бога, создавшего все на свете? Пенроуз смеется, вспоминая, как он опасался, что его гипотеза вызовет недовольство Церкви, в точности как в случае Галилея, которого он считает своим героем.
– Я читал лекцию в Ватикане, и мне было слегка не по себе. Но потом я понял, что они почитают Галилея и его изобретение астрономического телескопа. И вот я рассказывал о своей теории временных циклов и подумал, что им может не очень понравиться, что Большой взрыв не был началом. Но они ответили: «Да нет, все в порядке… Все это создал Бог».
Вне времени
Ответ Ватикана отсылает к вопросу, который давно занимает религиозных мыслителей: каковы отношения Бога со временем, особенно с учетом наших современных открытий его текучей природы? Специальная теория относительности Эйнштейна вообще ставит под вопрос возможность говорить о том, что одно событие происходит раньше другого. С одной точки зрения событие А происходит прежде события В, но, как показал Эйнштейн, с другой точки зрения может казаться, что событие В произошло первым.
Тут возникает интересная задача для богословов: какова точка зрения Бога? Считает ли Бог, что событие А произошло до события В или наоборот? Один из ответов совпадает с тем, что сказал Пенроузу представитель Ватикана: Бог существует вне времени. Раз Бог не находится в какой-то одной точке пространства, нет нужды ограничивать его и определенной точкой времени.
Сторонний наблюдатель мог бы видеть пространство-время так же, как человек, стоящий на вершине горы, видит внизу окружающую ее местность. Но такое видение пространства-времени должно охватывать разом прошлое, настоящее и будущее, все время сразу. Эту точку зрения выражал в IV в. богослов, известный под именем блаженного Августина Иппонийского, хотя и не используя терминологию четырехмерной геометрии Лоренца.
Эйнштейн пытался использовать эту точку зрения на время для утешения вдовы своего друга Мишеля Бессо. Он писал ей: «Он ушел из этого странного мира немного раньше меня. Это ничего не значит. Тот, кто подобно нам верит в физику, знает, что различие между прошлым, настоящим и будущим – лишь неуступчиво настойчивая иллюзия». То, что мы существуем в данном моменте времени, значит не больше, чем то, что мы находимся, скажем, в Лондоне, а не в Париже.
Но некоторые богословы не могут согласиться с тем, что Бог существует вне времени, потому что это не позволяет Богу действовать в мире. Для тех, кто выбирает теизм, а не простой деизм, Бог должен обладать временны́ми свойствами, чтобы иметь возможность вмешиваться в дела мира. Если Бог находится вовне, обозревая все пространство-время, то будущее уже существует в этом пейзаже. Что интересно, хотя о последовательности событий можно спорить, никто не станет спорить о ней, если между такими событиями существует причинно-следственная связь. Для этого нужно, чтобы Бог вступал во время и выходил из него, формируя геометрию пространства-времени. Но Бог, действующий в мире, есть Бог, действующий во времени. Поэтому очень трудно примирить идею вневременного Бога с идеей Бога, действующего во Вселенной.
По-прежнему остается без ответа тот же вопрос: что есть Бог, если предполагается, что он существует вне времени? Может ли что-либо быть вне времени? Вообще говоря, я готов признать вневременной одну вещь – математику. И в своем вневременном качестве она отлично подходит на роль инициатора творения, который дал нам пространство-время и возможность получать нечто из ничего. Математика обладает одним привлекательным качеством: можно не спрашивать, кто сотворил математику. Она существует вне времени и не нуждается в моменте сотворения. Она просто есть. Может быть, нам стоит вернуться к старому афоризму, утверждающему, что «Бог – математик». Если заменить в сформулированной Аквинатом попытке определения слово «Бог» на слово «математика», получится, по-моему, совсем неплохо: «Математику следует считать существующей вне области существования, причиной, из которой происходит все существующее в различных формах».
Это близко к идее гипотезы математической Вселенной (ГМВ), которую выдвинул физик-теоретик Макс Тегмарк. Он предположил, что наша физическая Вселенная есть абстрактная математическая структура. Такой своего рода современный вариант пифагорейской философии. Его статья, в которой он предлагает идею такой математической Вселенной, завершается следующим пассажем:
Если ГМВ верна, то это великолепная новость для науки: это позволяет надеяться, что в один прекрасный день изящное объединение физики, математики и информатики даст нам, людям, возможность получить понимание реальности, более глубокое, чем все, о чем мы когда-либо смели мечтать.
Я, наверное, не стал бы заходить так же далеко, как Тегмарк, и отождествлять физическую Вселенную с математикой. Например, с математической точки зрения было бы трудно отличить друг от друга две вселенные, в которых положительный и отрицательный электрические заряды поменялись местами. Физически такие вселенные будут разными, но их математическое описание будет совершенно одинаковым. Это пример так называемого «квиддитизма», идеи о том, что Вселенная не сводится к взаимоотношениям между объектами, – то, что́ они есть (латинское слово quid и означает «что»), добавляет еще один уровень различий.
Если математика вечна и находится вне времени, то для запуска развития мира не нужен создатель. Математические уравнения действительно существуют вне Вселенной, так что они могут играть роль чего-то сверхъестественного и богоподобного. Однако они – не Бог, действующий в мире, такое видение было бы деистическим. В таком случае интересно было бы задать вот какой вопрос: сколько существует разных способов организации вселенной на основе одного и того же набора математических уравнений? Множественные вселенные возникают сейчас из мультиматематических моделей.
Некоторые считают, что сам факт получения уравнения, согласно которому число единорогов увеличивается от нуля до трех в секунду, не означает, что единороги существуют. Поэтому наличие уравнений, допускающих существование кварков и их взаимодействие с различными полями, не делает кварки сколько-нибудь более реальными, чем единороги. Хокинг называет это необходимостью понимания «как вдохнуть в уравнения огонь». Например, как получилось, что отрицательный и положительный заряды в нашей Вселенной именно таковы, а не поменяны местами? Откуда взялось «квид» в слове «квиддитизм»?
Мне кажется, что если бы не было ни Вселенной, ни материи, ни пространства, ни вообще ничего, математика все равно существовала бы. Для существования математики не требуется физический мир. Поэтому, с моей точки зрения, математика – в высшей степени вероятный кандидат на роль первоначала. Это также объясняет и «непостижимую эффективность математики». Этим выражением Юджин Вигнер обозначил невероятную способность математики объяснять физические явления. Если физические явления – результаты математических построений, то в том, что мы находим все новые и новые математические объяснения самой сущности той Вселенной, в которой мы живем, нет ничего удивительного.
Время как выражение неполноты знания
Некоторые хотели бы, чтобы мы вообще покончили с необходимостью говорить о времени. Мои часы идут и идут. Сейчас они показывают чуть больше половины одиннадцатого вечера. Но что это значит? Стоит поместить другие часы, показывающие то же время, на космический корабль, и по возвращении они уже не будут совпадать с моими.
Из открытий Эйнштейна следует, что мы можем лишь сравнивать ход разных часов. Никакие часы не измеряют абсолютное время. Такое понятие просто не имеет смысла. Если вдуматься, станет ясно, что так было всегда. Как Галилей выяснил, что колебания маятника – хорошее средство измерения времени? Он сидел на мессе и наблюдал, как люстра, висевшая в церкви, качается на ветру. Когда он сопоставил ее колебания со своим пульсом, он понял, что период колебаний не зависит от угла размаха люстры. Но Галилей сравнивал одну меру времени с другой, которую он считал постоянной. На самом деле все эти устройства, измеряющие время, измеряют его лишь друг относительно друга.
Если вернуться к физическим уравнениям, то, хотя время играет в них важную роль, все их можно переписать, вообще не ссылаясь на время. То, что мы так сильно чувствуем течение времени, кажется, сделало его наиболее очевидным для нас окном для наблюдений за миром. Все книги по механике посвящены развитию Вселенной во времени. Уравнения траектории полета мяча используют время в качестве входного параметра и выдают в качестве результата координаты места, в котором этот мяч можно найти. Но ни одна из книг не определяет, что такое время, и ни один физик не установил четко и удовлетворительно, что мы понимаем под временем, так что, возможно, лучше всего было бы вовсе исключить его из рассмотрения.
Такова была цель, которую поставил перед собой физик Джулиан Барбур. Не занимая никакой научной должности, зарабатывая на содержание своей семьи переводами с русского, Барбур разработал теорию физической картины мира, в которой вовсе не было необходимости во времени. Он изложил свои идеи в революционной книге «Конец времени» (The End of Time: The Next Revolution in our Understanding of the Universe), опубликованной в 1999 г. «Ничего не происходит; есть бытие, но нет становления. Течение времени и движение являются иллюзиями». Довольно многие физики, работающие в традиционных научных учреждениях, восприняли его идеи в высшей степени серьезно.
Но тогда почему же я чувствую, что нечто, называемое временем, продолжает течь и я нахожусь в его власти? Я ощущаю, что не могу вернуться во времени вспять, что будущее ждет своей очереди случиться. Я помню прошлое, но не помню будущего. Итальянский физик Карло Ровелли и французский математик Ален Конн считают, что такое ощущение есть результат неполноты знания. Их так называемая тепловая гипотеза времени утверждает, что время – эмерджентное, вторичное явление, а не фундаментальная концепция.
Если взять любую физическую систему – например молекулы газа, находящиеся в моей комнате, – то, как правило, мы не имеем полного знания микроскопического состояния этих молекул. У нас есть только макроскопическое статистическое описание, допускающее возможность существования множества разных микроскопических состояний. Мы вынуждены рассматривать такую ситуацию статистически из-за неполноты нашего знания. Ровелли и Конн смогли показать математически, как такое неполное знание порождает поток, имеющий все те свойства, которые мы ассоциируем с ощущением течения времени. Они считают, что время возникает из макроскопического рассмотрения неизвестных микроскопических систем. Если проникнуть в такую систему достаточно глубоко, время исчезнет подобно тому, как идея поверхности жидкости теряет смысл на атомарном уровне структуры этой жидкости. Можно также вспомнить о бессмысленности рассуждений о температуре атома или о влажности молекулы воды. Время – тоже не фундаментальное, а такое же эмерджентное свойство.
Все это не значит, что эти вещи не существуют в реальности. Температура, влажность, ход времени. Я смотрю на часы. С их циферблата на меня смотрят цифры 23:55. Заканчивается еще один день. Вот-вот пробьет полночь, возвещая конец праздника и принося ощущение, что я еще на один день приблизился к тому моменту, когда я уже ничего не смогу знать. Но почему я вообще что-то ощущаю – течение времени, боль в ушибленном пальце, удовольствие от вкуса хорошего вина, восторг от музыки Прокофьева? Все это составляет самую суть одного из величайших из неразрешенных и, возможно, неразрешимых вопросов науки – как мы увидим на следующем «рубеже».
Назад: 9
Дальше: Рубеж шестой: Виртуальный собеседник

