Книга: О том, чего мы не можем знать. Путешествие к рубежам знаний
Назад: Рубеж четвертый: Бумажная Вселенная
Дальше: 8
7
Я осмеливаюсь предложить такое решение этой вековой проблемы: Библиотека безгранична и периодична. Если бы вечный странник пустился в путь в каком-либо направлении, он смог бы убедиться по прошествии веков, что те же книги повторяются в том же беспорядке. Эта изящная надежда скрашивает мое одиночество.Хорхе Луис Борхес. Вавилонская библиотека
Меня всегда занимал вот какой вопрос: существует ли физическая бесконечность? Мои попытки создать бесконечность путем деления игральной кости на бесконечно малые части потерпели неудачу, когда я добрался до неделимых кварков. Похоже, что даже пространство невозможно делить бесконечно, так как пространство квантуется. Поэтому теперь я собираюсь обратить свои поиски существования бесконечности в другую сторону – не внутрь, а наружу.
Что произойдет, если постоянно двигаться по прямой? Можно ли бесконечно продолжать такое движение? Я думаю, что этот вопрос хоть раз в жизни задавал себе всякий, кто когда-нибудь смотрел в пространство. Если бросить нашу игральную кость в космос, вернется ли она когда-нибудь в начальную точку, или натолкнется на космическую стену и отскочит обратно, или же так и будет вечно лететь, кувыркаясь в вакууме? Вопрос о том, бесконечно ли продолжается Вселенная, оказывается на удивление непрост и связан с тем обстоятельством, что само пространство не статично. Даже если Вселенная и бесконечна, могут существовать теоретические ограничения размеров пространства, доступного для нашего исследования. Возможно, мы никогда этого не узнаем.
Для помощи в путешествии в бесконечность я обзавелся своей собственной Вселенной – точнее, той ее частью, которую я могу увидеть. Я склеил себе звездный глобус, скачанный с веб-сайта Европейского космического агентства. Собственно говоря, это не вполне глобус. Он сделан из двух листов бумаги формата А4, из которых я вырезал и склеил одно из моих любимых геометрических тел – икосаэдр, состоящий из двадцати равносторонних треугольников. Как и кубик из казино, он является одним из пяти Платоновых тел, из которых получаются хорошие игральные кости.
Если ясной ночью посмотреть на небо, кажется, что все звезды нарисованы на огромной черной сфере, охватывающей Вселенную. Именно такую модель Вселенной использовали многие древние культуры. Они верили, что Земля находится в центре этой сферы, которая вращается вокруг оси, проведенной через Полярную звезду, единственную из звезд ночного неба, которая кажется неподвижной, в то время как все прочие звезды обращаются вокруг нее.
Мой бумажный звездный глобус – это модель такого небесного свода. Я поставил его на стол так, чтобы Полярная звезда оказалась в верхней точке икосаэдра. В середине глобуса нанесены знаки Зодиака, отмечающие последовательность месяцев года, – в том числе, разумеется, и мой собственный знак Девы. Нам кажется, что Солнце последовательно перемещается через все эти созвездия, возвращаясь в исходную точку к началу следующего года. В нижней половине глобуса расположены звезды, которые можно увидеть в Южном полушарии; самая яркая из них – Альфа Центавра. На самом деле она состоит из трех звезд, в число которых входит Проксима Центавра, считающаяся ближайшей к нашей собственной звезде, Солнцу.
Разнообразные варианты моего бумажного глобуса делали на протяжении многих тысячелетий. Цицерон пишет, что древнегреческие астрономы изготавливали модели небесного свода, на которых были отмечены звезды, – это были далекие предки моей бумажной Вселенной. К сожалению, ни одна из таких греческих моделей не дошла до нас, но в одном из моих самых любимых оксфордских музеев, в Музее истории науки, можно увидеть другие, сохранившиеся модели. Там есть великолепный глобус высотой около полуметра, сделанный в начале XVI в. в Германии. Созвездия на нем оживают в виде фигур птиц, рыб, животных и людей, напечатанных на бумажных сегментах и наклеенных на сферу.
Хотя моя современная бумажная модель не может сравниться красотой с глобусом XVI в. из Музея истории науки, его икосаэдральная форма восходит к Платону и его вере в то, что небесная оболочка, заключающая в себе нашу Вселенную, может быть не сферой, а додекаэдром – еще одним Платоновым телом, подходящим для игральных костей. И значение этой математической кости для понимания формы Вселенной может быть не таким надуманным, как кажется на первый взгляд.
Треугольные телескопы
Удивительно, что мы вообще что-то знаем о тех областях пространства, в которые мы никогда не сможем попасть. Люди всех культур неизменно смотрели в небо и размышляли о том, что там может быть. Присутствие Солнца и Луны становится очевидным прежде всего. Но как же древним культурам удалось открыть что-то об этих небесных телах, если они были прикованы к поверхности планеты? Я вижу в этом одно из самых замечательных свойств математики – она позволяет нам делать выводы об устройстве Вселенной, не выходя из наших уютных обсерваторий.
Тригонометрия, математика углов и треугольников, была разработана не для того, чтобы мучить школьников, а для ориентации в ночном небе. Она стала нашим первым телескопом. Еще в III в. до н. э. Аристарх Самосский смог вычислить отношение размеров Солнца и Луны к радиусу Земли и определить соотношение их удалений от Земли, используя лишь математические модели треугольников.
Например, когда Луна находится точно в первой или последней четверти, угол между Землей, Луной и Солнцем приблизительно равен 90°. Тогда, измерив угол Φ между Луной, Землей и Солнцем, можно вычислить отношение расстояний между Землей и Луной и между Землей и Солнцем методами тригонометрии. Отношение этих расстояний точно равно косинусу угла Φ, то есть определяется чисто математическими методами.

Прямоугольный треугольник, образуемый Землей, Луной и Солнцем в первой и последней четвертях Луны
Однако точность измерений Аристарха была такова, что определенное им соотношение расстояний отличалось от точного результата в 20 раз. По его оценке, угол был равен 87°, в то время как его истинное значение составляет 89,853°, что почти равно прямому углу. Малое отклонение значения угла такой величины приводит к довольно большому изменению соотношения длин сторон треугольника. Для истинного определения размеров Солнечной системы потребовалось изобретение телескопа и более замысловатых математических методов.
Даже и не имея телескопов, астрономы видели, что Луна и Солнце – не единственные тела, перемещающиеся по небу. Древние культуры заметили в ночном небе несколько светящихся точек, которые вели себя совершенно иначе, чем множество прочих звезд. Они – Меркурий, Венера, Марс, Юпитер и Сатурн – казались блуждающими световыми маяками, которые нельзя отметить на моей бумажной сфере, поскольку на следующую ночь они окажутся уже в других точках. Одно из объяснений того важного значения, которое число семь имеет для разных культур, связано с тем, что число видимых планет с добавлением Солнца и Луны равно именно семи.
Борьба с бесконечностью
Не только планеты каждый день перемещаются относительно звезд, – оказывается, что и звезды движутся друг относительно друга. Так что небесный свод на моем столе – всего лишь моментальный снимок состояния ночного неба на некоторый определенный момент. Например, на моей сфере отмечено легко узнаваемое созвездие Большой Медведицы. Но звезды, образующие Большую Медведицу, – Мерак, Дубхе, Алькаид (Бенетнаш), Фекда, Алиот и Мицар – находятся в движении: 100 000 лет назад они образовывали бы на моем глобусе совсем другой рисунок, и еще через 100 000 лет они тоже будут выглядеть по-другому.
Но древние астрономы считали, что звезды неподвижны, прикреплены к небесному своду, заключающему в себе Вселенную. Вопрос о том, что лежит за пределами этой сферы, практически не обсуждался. За ней была пустота, не содержащая ничего. Пространство вне моей бумажной модели было недоступно. Однако находились и такие средневековые философы, которые были готовы размышлять о природе этой пустоты. Николай Орем полагал, что за пределами небесного свода существует дальнейшее космическое пространство бесконечной протяженности. В своих работах он отождествлял это бесконечное пространство с Богом – что, возможно, не так уж и далеко от концепции Бога как того, чего мы не можем знать, которую я предлагал выше.
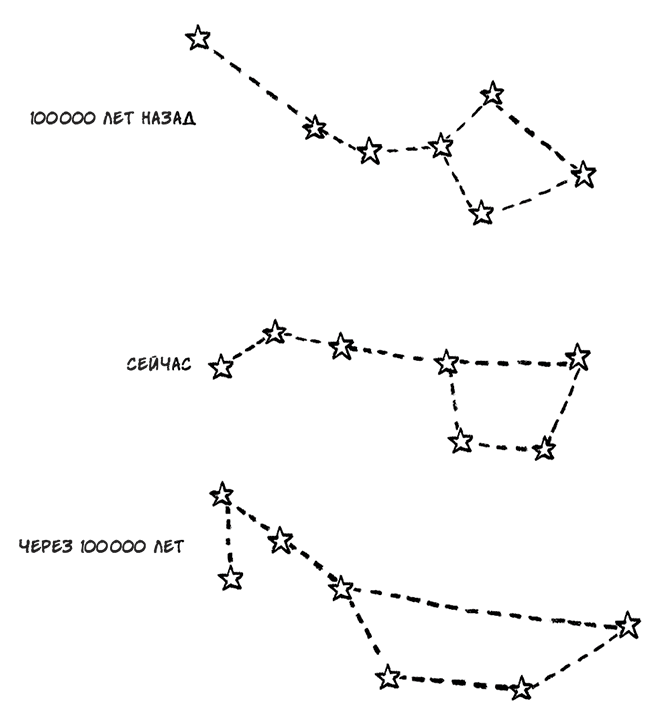
Изменяющаяся форма Большой Медведицы
Философские трудности проблемы бесконечности не пугали Орема. Так, он доказал, что сложение дробей 1 + 1/2 + 1/3 + 1/4 + … дает бесконечность – результат интуитивно не очевидный, поскольку добавляемые слагаемые становятся все меньше и меньше. Эта бесконечная сумма называется гармоническим рядом, потому что звук, извлекаемый из струны виолончели, составлен из гармоник, длины волн которых равны всем этим дробям. Как я объясню далее, то обстоятельство, что сумма такого гармонического ряда равна бесконечности, интересным образом влияет на то, как далеко мы в принципе можем заглянуть в пространство.
По-видимому, только в XV в. астрономы начали задумываться о том, что небесный свод может быть иллюзией, а Вселенная может простираться бесконечно. Николай Кузанский предположил, что Вселенная бесконечна и потому ее центром может считаться любая ее точка. Эту идею подхватил итальянский монах-доминиканец Джордано Бруно, написавший в 1584 г. эпохальную работу «О бесконечности, Вселенной и мирах».
Итак, Вселенная едина, бесконечна, неподвижна […] Она никоим образом не может быть охвачена и поэтому неисчислима и беспредельна, а тем самым бесконечна и безгранична и, следовательно, неподвижна.
Интересна логика, приведшая Бруно к такому выводу. Вселенная создана Богом, но Бог непознаваем. Поэтому Вселенная должна быть недоступна нашему пониманию. Следовательно, она должна быть бесконечной, так как конечная Вселенная была бы теоретически познаваемой. Я бы сказал, что верно обратное: если Вселенная бесконечна, это означает, что она может быть недоступна нашему пониманию. И если исследовать концепцию Бога как способа выражения непознаваемого, то из бесконечности Вселенной, если она действительно непознаваема, могло бы следовать существование такой концепции трансцендентности. Но бесконечна ли Вселенная, и если она бесконечна, то так ли она непознаваема, как кажется на первый взгляд?
Бруно основывает свое мнение о бесконечности Вселенной не только на вере в Бога. Одно из наиболее сильных возражений против конечности Вселенной, заключенной внутри небесного свода, сводится к вопросу о том, что находится за стенкой, заключающей в себе такую Вселенную. Многие предполагали, что за ней находится ничто, пустота. Но Бруно такой ответ не устраивал. Он считал еще, что время также простирается бесконечно – как в прошлое, так и в будущее. Такая, хотя и небесспорная, концепция позволяла избавиться от необходимости существования моментов Сотворения мира и Страшного суда. Споры Бруно не страшили, и его толкование Библии в конце концов поссорило его с католической церковью, что в то время было довольно неприятным обстоятельством. 17 февраля 1600 г. его сожгли на костре.
Идеи Бруно поднимают вопрос о самой возможности знания о бесконечности Вселенной. Если она конечна, то об этом, вероятно, можно узнать. Если поверхность Земли оказалась конечной и достижимой, не можем ли мы, путешествуя по Вселенной, доказать, что она конечна? Хотя у нас нет корабля, на котором мы могли бы отправиться на край Вселенной, ученые XVII в. изобрели остроумное средство исследования космоса – телескоп.
Далеко ли вы видите?
Тот факт, что искривленные стеклянные линзы, установленные внутри трубки, позволяют увеличить дальность зрения, был открыт поколением Галилея. Долгие годы честь изобретения телескопа приписывалась даже самому Галилею, но на самом деле она принадлежит голландскому очковому мастеру Иоганну Липперсгею, взявшему патент на прибор «для видения вещей удаленных, как если бы они были вблизи». Этот голландский прибор обеспечивал трехкратное увеличение.
Галилей узнал об этом приборе во время поездки в Венецию. Тем же вечером он разобрался в принципах его работы и вскоре уже изготавливал приборы, увеличение которых доходило до 33-кратного. Название «телескоп» придумал один греческий поэт, присутствовавший в 1611 г. на банкете в честь Галилея: τῆλε (теле) переводится с греческого как «далеко», а σκοπέω (скопео) – «смотрю». Действительно, телескоп позволил Галилею и последующим поколениям астрономов смотреть дальше, чем когда-либо. Галилей открыл луны, обращающиеся вокруг Юпитера, и пятна на Солнце, вращение которых свидетельствовало о том, что и Солнце вращается вокруг собственной оси. Эти явления послужили подтверждением модели гелиоцентрической Солнечной системы, предложенной Коперником.
В 1663 г. шотландский математик Джеймс Грегори осознал, что телескоп можно использовать, чтобы заново вычислить расстояние от Солнца до Земли. Иоганн Кеплер уже измерил время обращения каждой из планет вокруг Солнца и определил при помощи своих законов планетарного движения соотношения расстояний между планетами и Солнцем. Его третий закон гласит, что квадрат времени обращения планеты вокруг Солнца пропорционален кубу расстояния от нее до Солнца. Например, Венера совершает оборот по своей орбите за 3/5 времени, которое занимает оборот Земли; это означает, что расстояние между Венерой и Солнцем составляет около 7/10 (точнее, (3/5)2/3) расстояния между Землей и Солнцем. Правда, нужно помнить, что говорить о расстоянии от Солнца следует с осторожностью: как установил Кеплер, планеты описывают вокруг него не точные окружности, но эллипсы, так что это расстояние изменяется. В общем случае я имею в виду нечто вроде среднего расстояния.
Однако речь по-прежнему шла об относительных расстояниях. Грегори и другие поняли, что на основе наблюдений прохождения Венеры по диску Солнца, так называемого транзита, при помощи некоторых дополнительных тригонометрических операций можно установить, на каком именно расстоянии от Солнца находятся Земля и Венера. Если из двух разных точек на Земле произвести наблюдения разных моментов и точек прохождения Венерой солнечного диска, то можно определить угол треугольника, образованного двумя наблюдателями и Венерой. А тогда тригонометрия позволяет, вычислив расстояние между двумя наблюдателями на Земле, определить расстояние до Венеры.
Тригонометрия замечательна тем, что дает возможность преобразовывать величины, непосредственно измерить которые невозможно, например расстояние от Земли до Венеры, в нечто, измеримое с поверхности Земли, например углы или расстояние между двумя точками на Земле. Это вычисление представляло собой сложное, но изобретательное применение абстрактной математической мысли в сочетании с практическими астрономическими наблюдениями.
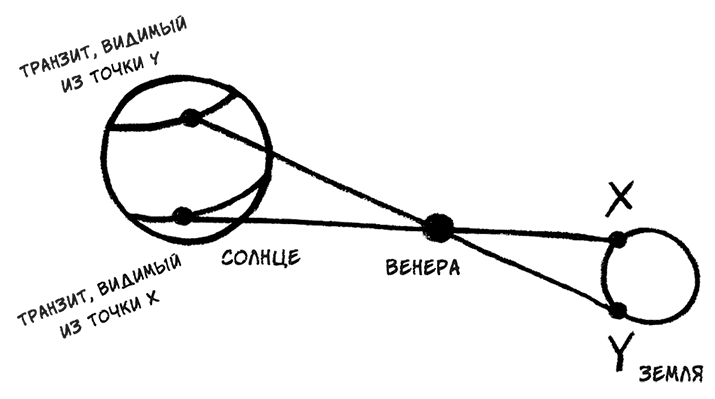
Прохождение Венеры, видимое из двух разных точек на Земле
Проблема заключалась в том, что такие транзиты случаются нечасто. С 1400 г. Венера проходила через диск Солнца всего десять раз. Грегори сначала предлагал использовать транзит Меркурия, так как следующее прохождение Венеры ожидалось лишь в 1761 г. Эдмонд Галлей знал о его работе и произвел наблюдения прохождения Меркурия, произошедшего в 1676 г. Однако оказалось, что кроме этого было произведено всего одно наблюдение: теоретически этого было достаточно для вычисления расстояния, но с учетом возможных ошибок число наблюдений следовало сделать как можно большим.
Расстояние от Земли до Солнца в конце концов смогли определить благодаря многочисленным наблюдениям прохождений Венеры в 1761 и 1769 гг. В ходе одного из первых согласованных всемирных научных экспериментов такого рода было вычислено, что Земля находится приблизительно в 153 000 000 км от Солнца. К сожалению, Галлей умер приблизительно за 19 лет до этого и не увидел кульминации проекта, который он пытался осуществить почти 90 годами раньше. Современные вычисления дают для среднего расстояния между Солнцем и Землей значение, равное 149 597 870 700 м.
Эти результаты дали первое представление о том, какие гигантские расстояния заключены в моем бумажном глобусе неба. Астрономы древности считали, что моя бумажная модель содержит меньшие глобусы, в которые вписаны планеты. Если бы они были правы, диаметры таких глобусов составляли бы миллионы километров.
Меня неизменно поражает способность тригонометрии преобразовывать измерения расстояний на Земле в измерения расстояний до планет, на которых никогда не бывал человек. Позднее последовали другие впечатляющие математические свершения. Телескопы и свет оказались не единственными инструментами для поисков того, что находится в космосе. Выяснилось, что математика тоже может увеличить дальность видения Вселенной, причем настолько, чтобы успешно предсказать существование новой планеты еще до того, как ее впервые увидят в окуляре телескопа.
Планета, открытая на кончике пера
Есть два средства открывать новые планеты – везение и логика. Первая со времен Античности вновь открытая планета была обнаружена благодаря везению. Немецкий музыкант Фридрих Вильгельм Гершель переехал из Ганновера в Англию, пытаясь сделать там карьеру в музыке. Но, кроме того, он был своего рода астрономом-любителем и по ночам изучал небо при помощи своей внушительной коллекции телескопов.
13 марта 1781 г. Гершель заметил нечто необычное. То, что сначала показалось ему звездой, изменяло размер в зависимости от увеличения телескопа. Как правило, это говорит о том, что данный объект находится настолько близко к наблюдателю, что масштаб его изображения может быть ощутимо изменен. Далее следовало проверить, движется ли этот объект. Действительно, четыре дня спустя Гершель увидел, что положение объекта относительно звезд изменилось. Учитывая количество комет, обнаруженных на тот момент, мысль об открытии новой планеты пришла ему в голову не сразу.
Но после того, как он сообщил о своей находке королевскому астроному и за найденным объектом стали следить, выяснилось, что он имеет орбиту не параболическую, как можно было бы ожидать у кометы, а практически круглую. Кроме того, объект был слишком ярок для кометы и не имел видимого хвоста. Астрономы заключили, что речь все-таки идет о новой планете. Гершель хотел назвать ее в честь короля Георга III, но классическая мифология одержала верх. Сатурн был отцом Юпитера, и новую планету, орбита которой была расположена еще дальше, назвали по имени отца Сатурна – Ураном.
Идея новой планеты привела астрономов в сильнейший восторг. Они начали наносить на карты ее траекторию, искать ее луны и рассчитывать период ее обращения вокруг Солнца. Но Уран оказался вовсе не столь послушным, как ожидали некоторые астрономы. Ньютонова теория гравитации, столь успешно предсказавшая орбиты других планет, то и дело не срабатывала, когда дело доходило до предсказаний положения Урана. К 1788 г. планета отклонялась от расчетного положения на 1/120°. Стало понятно, что необходимо учесть гравитационное воздействие на нее Юпитера и Сатурна.
Новая траектория была опубликована в 1791 г., но к 1800-му обнаружились отклонения и от нее. К 1825 г. Уран ушел далеко вперед от предсказанного положения, но затем начал замедляться и к 1832 г. отстал от математических предсказаний. Могло ли дело быть в том, что его движению мешает некое таинственное вещество? Или же законы гравитации Ньютона на таком большом расстоянии от Солнца начинают нарушаться? Некоторые предполагали, что может существовать еще одна планета, замедляющая и ускоряющая движение Урана подобно тому, как Юпитер и Сатурн создают воздействующее на него гравитационное притяжение. Но если такая планета существует, где же она?
Если открытие Урана было удачей, то эту новую планету нужно было найти силой чистой логики, воплощенной в математике Ньютона. До сих пор астрономы брали известное положение планет и использовали математические формулы для расчета их орбит. Теперь эту процедуру нужно было запустить в обратном направлении. За движением Урана следили несколько десятилетий, и задача состояла в определении такого места, в котором могла бы находиться планета, объясняющая странности траектории Урана.
С математической точки зрения задача была чрезвычайно непростой, но нашлись два теоретика, которые приняли этот вызов: это были Джон Куч Адамс в Англии и Урбен Леверье во Франции. Им обоим удалось обратить задачу и определить, где, по их мнению, могла находиться новая планета. К сентябрю 1845 г. Адамс завершил свои вычисления и обратился к английским астрономам, чтобы они попытались найти новую планету. Видимо, отсутствие у Адамса солидной репутации и его довольно нелюбезные манеры (возможно, проявление синдрома Аспергера) не внушали авторитетным ученым особого доверия. Королевский астроном был к тому же отвлечен скандальным делом об убийстве, в котором был замешан один из его ассистентов. В результате на английском берегу Ла-Манша предсказания Адамса оставили без внимания. Леверье закончил свои расчеты только в июне 1846 г. и также натолкнулся на невозможность убедить руководство французских обсерваторий в необходимости тратить ценное время работы телескопов на поиски гипотетической планеты. Поэтому Леверье обратился за помощью в Берлинскую обсерваторию.
Немецкие астрономы оказались более отзывчивыми. 23 сентября 1846 г. Иоганн Готфрид Галле направил свой телескоп, изготовленный компанией Фраунгофера, в то место ночного неба, в котором, по расчетам Леверье, должна была находиться новая планета. И благополучно обнаружил в нем светящуюся точку, не нанесенную ни на какую из звездных карт, бывших в обсерватории. На следующую ночь точка переместилась… в точности на то расстояние, которое предсказывали вычисления Леверье.
Многие встретили сообщение об открытии очередной планеты с энтузиазмом, но английские астрономы, не сумевшие развить успех Адамса, выглядели довольно глупо. Гершель, ставший к этому времени членом Наблюдательного совета Королевской обсерватории в Гринвиче, попытался собрать доказательства того, что Адамс сделал свое предсказание первым. Это привело к еще более яростному спору за приоритет. Наименование планеты превратилось в политический футбол: французы хотели назвать ее в честь Леверье, а англичане возражали против нарушения традиции наименования планет именами римских богов. В конце концов международное сообщество сошлось на названии Нептун.
Могущество математики, позволяющее ей делать подобные предсказания, удивительно. Как иронично заметил астроном Франсуа Араго, Леверье открыл Нептун «на кончике своего пера». Разумеется, для подтверждения соответствия его теории реальности потребовались наблюдения, которые Галле произвел в Берлинской обсерватории.
Будучи прикованы к поверхности Земли, мы тем не менее смогли достичь края Солнечной системы. На какое же расстояние можно исследовать дальнейшее пространство? Хотя телескопы позволили нам дойти до этой точки, они также выявили, что у дальности нашего зрения существуют теоретические пределы, поскольку, как выяснилось, свету требуется некоторое время, чтобы добраться до нас.
Космическое ограничение скорости
Телескоп сыграл решающую роль в разрешении одного спора, не утихавшего со времен Античности. Распространяется ли свет в пространстве мгновенно, или же его перемещение из одного места в другое занимает какое-то время? Аристотель, например, не верил, что свет движется. Либо он есть, либо его нет. Другие соглашались с ним. Древние греки полагали, что зрение сводится к перемещению света из глаза на видимый объект. Если это так, рассуждал математик Герон Александрийский, то свет должен распространяться мгновенно. Иначе как мы можем, открыв глаза, сразу видеть далекие звезды?
Идею о том, что свет движется в обратном направлении, от объекта к глазу, предложил в своей «Книге оптики» арабский ученый Ибн аль-Хайсам. Но даже если свет и перемещается в обратном направлении, многие по-прежнему считали, что он распространяется с бесконечно большой скоростью. Однако Галилей не был в этом уверен. Он предположил, что если распространение света от источника занимает некоторое время, то это время наверняка можно измерить. Он предложил открывать светильник и отмечать, через какое время его станет видно на расстоянии нескольких миль. Масштаб, предложенный Галилеем, был слишком мал, чтобы заметить какую-либо задержку; Декарт увеличил его. Он понял, что если перемещение света к Земле от Солнца и от Луны занимает какое-то время, то время наступления лунных затмений должно несколько отличаться от ожидаемого. Однако таких отклонений обнаружено не было. И Галилей, и Декарт были правы: просто свет распространяется так быстро, что расстояния до Солнца и Луны были все еще слишком малы, чтобы какие-либо расхождения можно было заметить.
Доказательство того, что распространение света в пространстве действительно занимает определенное время, было в конце концов получено не от нашей Луны, а от лун, обращающихся вокруг Юпитера. Галилей предложил использовать луны Юпитера в хитроумном решении проблемы определения долготы. Для этого нужно было измерять время, используя момент входа Ио, ближайшего к Юпитеру спутника, в тень этой планеты. Ио обращается вокруг Юпитера за 42,5 часа, достаточно регулярно, чтобы служить космическими часами. Если составить таблицу времен, в которые такие затмения видны из Флоренции, то, измерив времена затмения в другом месте, можно определить его долготу относительно Флоренции. Этот метод не прижился для определения долготы на море – а в то время это было важной нерешенной задачей, – но использовался для определения долготы на суше.
В 1676 г. датский астроном Оле Рёмер открыл конечную скорость света при помощи лун Юпитера. Работая в Парижской обсерватории, он отмечал время, в которое Ио исчезала в тени Юпитера. Оказалось, что такое время зависит от положения Земли на орбите вокруг Солнца. Когда Земля и Юпитер находились по разные стороны от Солнца, наблюдалась задержка. Рёмер понял, что она связана с тем, что прохождение света до Земли занимает больше времени, чем в случаях, в которых Земля и Юпитер находятся с одной и той же стороны от Солнца. Об открытии объявил 22 августа 1676 г. в Королевской академии наук Парижа директор обсерватории Джованни Кассини. Он объяснил, что астрономам придется изменить таблицы, предсказывающие время затмений Ио:
Это, вероятно, связано с тем, что свету требуется какое-то время, чтобы дойти от спутника до наблюдателя; для пересечения расстояния, равного половине диаметра земной орбиты, свету, по-видимому, требуется от десяти до одиннадцати минут.
Согласно современным измерениям, это время равно 8 минутам и 20 секундам, так что астрономы XVII в. были недалеки от истины. Затем последовал целый ряд экспериментов по определению численного значения скорости света в безвоздушном пространстве. Поскольку скорость света составляет около 300 миллионов метров в секунду, неудивительно, что многие считали ее бесконечной. С появлением телескопов, позволяющих измерять огромные космические расстояния, скорость света стала существенным ограничением любых попыток заглянуть в дальние пределы Вселенной.
Более того, то обстоятельство, что для пересечения пространства свету требуется определенное время, означает, что, когда мы смотрим во Вселенную, мы смотрим в прошлое. Солнце изображается на фотографии неба таким, каким оно было 8 минут и 20 секунд назад, ближайшая звезда – четыре года назад, а наиболее удаленные галактики – миллиарды лет назад. Возможно, в какой-нибудь далекой галактике в сторону Земли обращены сейчас телескопы, в которые видно вымирание динозавров, произошедшее около 66 миллионов лет назад.
Скорость света стала использоваться астрономами для измерения гигантских космических расстояний. Когда астроном говорит о чем-то, находящемся на расстоянии одного светового года, это значит, что свет может дойти до нас из этой точки за один год.
Звезды по соседству
Когда я смотрю на свою настольную небесную сферу, мне кажется смешным, что древние греки считали звезды нарисованными на огромном сферическом небесном своде, окружающем Вселенную и окруженном пустотой. Но у них не было оснований думать иначе. Расстояния от Земли до звезд так велики, что невооруженному глазу все звезды кажутся просто очень далекими. Астрономы древности не имели никаких средств измерения глубины космоса. Однако изобретение телескопа несколько приблизило к нам эти звезды – настолько, что современные астрономы смогли увидеть, что не все они находятся на одинаковом расстоянии от Земли.
Если одна из звезд находится ближе к нам, чем другая, то существует возможность это установить. Хотя мы и прикованы к поверхности Земли, по крайней мере сама Земля движется относительно звезд, отчего мы можем смотреть на космос из разных точек. Это-то и дало нам возможность начать отклеивать некоторые из звезд от поверхности небесного свода и придавать Вселенной глубину.
Вытяните перед собой палец и посмотрите в окно, двигая головой из стороны в сторону. Вы заметите, что предметы, расположенные ближе к вам, – например ваш собственный палец – смещаются на большее расстояние, чем объекты более удаленные. Этот эффект называют параллаксом. Астрономы используют его в своих наблюдениях за звездами. Сравнивая положения звезд летом с их положениями зимой, они могут определить, какие из них находятся ближе к Земле.
Собственно говоря, Гершель открыл свою новую планету, Уран, именно пытаясь определить этот так называемый звездный параллакс. Различия в положениях звезд чрезвычайно малы, и для выявления такого сдвига необходимы телескопы достаточной точности. Первые успешные измерения были произведены только в 1830-х гг., когда немецкий астроном и математик Фридрих Бессель зарегистрировал первое точное наблюдение звездного параллакса. Чтобы применить эту технику к близлежащим звездам, астроном должен предположить, что удаленные звезды, по существу, находятся на единой небесной стене, охватывающей Вселенную, – приблизительно в соответствии с древнегреческой моделью. Дело в том, что в контексте задачи определения параллакса близлежащих звезд наиболее удаленные звезды кажутся неподвижными и их можно использовать в качестве фона, на котором выявляют движение звезд не столь удаленных.
Бессель сравнил летнее и зимнее положения звезды под названием 61 Лебедя, построил треугольник, образованный этой звездой и двумя соответствующими точками орбиты Земли, и рассчитал углы этого треугольника. Затем, используя известное расстояние от Земли до Солнца и математические методы тригонометрии, астрономы смогли получить первую оценку расстояния между ближайшими звездами и Землей. В соответствии с вычислениями Бесселя звезда 61 Лебедя находится в 660 000 раз дальше от Земли, чем Солнце. Ошибка его расчетов составила около 10 %. По современным данным, расстояние до 61 Лебедя в 721 000 раз больше расстояния от Земли до Солнца и составляет 11,41 светового года. Но результаты, полученные Бесселем, были достаточно близки к истине, чтобы дать первое представление о глубине космоса.
Впоследствии были произведены расчеты положения еще более близких звезд. Ближайшая из известных нам звезд была замечена только в 1915 г. шотландским астрономом Робертом Иннесом. Свет Проксимы Центавра слишком слаб, чтобы ее можно было увидеть невооруженным глазом, что и было причиной столь позднего ее обнаружения. Однако вычисления ее параллакса показали, что эта звезда находится на расстоянии, превышающем расстояние от Земли до Солнца в 268 326 раз, то есть равном 4,24 светового года.
Метод звездного параллакса позволил начать отцеплять некоторые из звезд от моей небесной сферы и приближать их к Земле. Если звезда находится менее чем в 400 световых лет от нас, этот метод работает. Но в большинстве своем звезды по-прежнему казались такими же далекими, как если бы они были приклеены к моей бумажной модели. Следующий большой шаг к краю Вселенной был сделан благодаря анализу длин волн света, доходящего до нас от этих звезд.
Среди миров, в мерцании светил
Чем дальше от нас находится звезда, тем менее ярким кажется ее свет. Но использование этого критерия для определения расстояния до звезды связано с одной проблемой. Как узнать, смотрим ли мы на яркую, но удаленную звезду, подобную 61 Лебедя, которую можно увидеть невооруженным глазом, или на звезду более тусклую, но и более близкую, подобную Проксиме Центавра? Видимую яркость определяет сочетание действительной яркости и расстояния от данной звезды до Земли. Как же астрономы могут использовать яркость для определения расстояний? Оказывается, что цвет света, испускаемого звездой, во многих случаях дает достаточно информации для выяснения, насколько яркой она должна быть, и, измерив ее видимую яркость, мы можем определить, на каком расстоянии находится эта звезда.
Измеряя характеристики света, доходящего от звезд, и анализируя его частоты, ученые обнаружили отсутствие некоторых характерных частот. Свет, имеющий такие частоты, поглощается определенными атомами в составе звезды. Этот метод стал ключевым доводом, опровергшим знаменитое заявление Конта о том, что мы никогда не сможем узнать химический состав звезд. Но его также можно использовать и для вычисления яркости звезды. Рассмотрев близлежащие звезды, удаленность и, следовательно, действительная яркость которых была известна, астрономы обнаружили непосредственную связь между частотами, поглощаемыми звездой, и яркостью ее свечения.
Из этого открытия следовало, что недостающие в спектре света звезды частоты можно использовать в качестве меры ее абсолютной светимости. Теперь астрономы могли изучать звезды, расположенные слишком далеко для применения метода параллакса. Определив их недостающие частоты и видимую светимость, можно было определить, на каком расстоянии от нас такие звезды находятся. Это дало астрономам гораздо более ясное представление об истинной глубине космоса.
Однако наилучший способ измерения расстояний во Вселенной был получен от весьма особой пульсирующей звезды. Звезды, называемые цефеидами, мерцают, и в 1912 г. американский астроном Генриетта Ливитт открыла, как такие мерцающие звезды можно использовать для ориентации во Вселенной. В это время она работала в обсерватории Гарвардского университета, но не астрономом, а «вычислителем» – она извлекала данные из фотопластинок и получала за эту работу 30 центов в час. К работе на телескопах женщин не допускали. Ей поручили проанализировать звезды, яркость которых в течение некоторого временного промежутка увеличивалась и уменьшалась. Ливитт стало интересно, существует ли какая-либо закономерность в пульсации этих звезд, и она сосредоточила свое внимание на группе звезд, которые были расположены в Малом Магеллановом Облаке, а потому, как предполагалось, находились на приблизительно одинаковых расстояниях от Земли.
Построив зависимость светимости от длительности периода пульсации, Ливитт обнаружила чрезвычайно явную закономерность. Время пульсации цефеиды коррелировало с ее светимостью: чем длиннее был период пульсации, тем ярче горела звезда. Таким образом, для определения действительной яркости цефеиды достаточно было измерить период ее пульсации, что значительно легче, чем измерять недостающие частоты ее спектра. Такие звезды идеально подходили для измерения расстояний.
Если такая цефеида пульсирует медленно, но выглядит тусклой, это означает, что она расположена очень далеко от нас; кажущаяся яркой и быстро пульсирующая цефеида выглядит такой яркой потому, что она находится близко. С появлением этих новых средств измерения Вселенная стала приобретать определенную форму. Все новые и новые звезды откреплялись от небесного свода и занимали свои места на постепенно проявляющейся карте Млечного Пути. При этом выяснилось, что наша собственная звезда, Солнце, ютится в дальнем углу гигантского спиралевидного скопления звезд.
Но ограничивается ли этим Вселенная? Например, в ней можно увидеть световые пятна, похожие не на одиночные звезды, а на свет, исходящий от сотен миллиардов звезд. Принадлежат ли такие звездные облака к нашей Галактике, Млечному Пути, или же они образуют другую галактику, подобную нашей, но совершенно отдельную от нее? Первой из таких областей космоса, ставшей предметом исследования, было маленькое звездное скопление, обнаруженное в X в. персидским астрономом ас-Суфи. Настолько яркое, что его можно было увидеть невооруженным глазом, оно стало известно как туманность Андромеды. Предположение о том, что это и другие облака могут на самом деле представлять собой самостоятельные галактики, было впервые высказано в 1750 г. английским астрономом Томасом Райтом. Прочитав об идеях Райта, Иммануил Кант выразил их в романтической формулировке «островной вселенной».
Споры о природе таких звездных облаков не утихали годами и достигли наивысшего накала в прямой дискуссии между противоборствующими группами, ныне известной под названием «Великого спора». Он проходил в 1920 г. в Национальном музее естественной истории Смитсоновского института в Вашингтоне. На повестке дня стоял вопрос о размере и масштабах Вселенной. Астроном Харлоу Шепли доказывал, что такие скопления могут светить настолько ярко, только если они являются частью нашей же Галактики. Гебер Кертис возражал, что число новых – катастрофических ядерных вспышек, происходящих в звездах, – отмеченных в этом скоплении, превосходит число подобных событий, зарегистрированных во всей нашей Галактике. Как настолько богатая новыми область может быть частью нашей Галактики?
В конце концов туманность Андромеды пришлось убрать из нашей Галактики: наблюдения американского астронома Эдвина Хаббла доказали, что она является самостоятельной галактикой, отдельной от нашей. В 1925 г. Хаббл работал в обсерватории Маунт-Вилсон в Калифорнии и использовал телескоп Хукера, крупнейший телескоп своего рода на этот момент, для анализа расстояния до туманности Андромеды.
Хаббл заметил, в частности, одну звезду, которую можно было использовать для вычисления этого расстояния. В центре туманности располагалась одна из цефеид, которые исследовала Ливитт. Эта звезда пульсировала, становясь тусклее и ярче с периодом в 31 день. Согласно анализу Ливитт, она должна была быть очень яркой, но в телескопе выглядела чрезвычайно тусклой. Сочетание периода пульсирования и измеренного значения видимой светимости звезды показало, что она находится на расстоянии 2,5 миллиона световых лет от Солнца. Максимальное расчетное расстояние между звездами Млечного Пути составляет 100 000 световых лет. Открытие Ливитт в сочетании с вычислениями Хаббла самым решительным образом изменило наше представление о Вселенной. Она оказалась значительно больше, чем кто-либо мог вообразить.
Предложенный Ливитт метод использования цефеид для исследования космического пространства настолько радикально преобразовал нашу картину Вселенной, что шведский математик Гёста Миттаг-Леффлер хотел номинировать ее на Нобелевскую премию 1924 г. К своему огромному огорчению, он выяснил, что в декабре 1921 г. Ливитт умерла от рака и премия не могла быть ей присуждена.
Такое новое понимание масштаба удаленных галактик дало нам представление об истинной природе космоса. Но насколько простирается Вселенная за пределами таких удаленных галактик? Первым земным исследователям, покидавшим свои деревни, наверное, казалось, что Земля огромна – возможно, бесконечна. Но по мере развития путешествий стало понятно, что поверхность Земли конечна и доступна для исследования. Так как же обстоит дело с космосом? Сможем ли мы, покинув свою Галактику, понять, какое место наша космическая деревня занимает в более масштабной картине космоса?
Гигантская игра в «астероиды»
Легко себе представить Землю конечную, но не имеющую края. Решение этой загадки – поверхность сферы. Но как может быть конечным космос? Эту головоломку исследует один из моих любимых фильмов – «Шоу Трумана». Джим Керри играет в нем Трумана Бербанка, который не подозревает о том, что весь его мир – сценарное телевизионное реалити-шоу, поставленное внутри гигантского купола. Когда у него в конце концов возникают сомнения относительно окружающего его мира, Труман садится в лодку и отправляется в море, окружающее его родной город Сихэвен, – и обнаруживает, что небо, которое казалось ему бесконечным, на самом деле нарисовано на студийном заднике. А за краем своей вселенной он находит телекамеры, снимающие каждое его движение.
Я не думаю, что мы живем в таком вот «Шоу Трумана». Я не думаю, что, отправившись в космос, можно неожиданно натолкнуться на стенку студии или на окружающий мир небесный свод, подобный моей модели. И мне кажется, что большинство людей со мной согласятся. В конце концов, такая модель только поднимает вопрос о том, что находится за этим пределом. Встретим ли мы там небесную съемочную группу, наблюдающую за нами? А что случится с этой съемочной группой, если она отправится в такое же путешествие в своем мире? Там что, съемочные группы до самого конца? Поэтому большинство из нас, будучи поставлено перед этим вопросом, заключает, что единственное возможное решение этой головоломки – бесконечная Вселенная.
Но у математиков есть еще и третий вариант, согласно которому Вселенная может не иметь границы, но тем не менее быть конечной. В такой Вселенной космическое путешествие не продолжается бесконечно далеко, но в конце концов возвращается в свою начальную точку подобно кругосветному путешествию на Земле.
Чтобы понять, как такая Вселенная может быть устроена, полезно рассмотреть маленькую игрушечную вселенную. Игра «Астероиды», созданная в 1979 г. компанией Atari, дает превосходный пример конечной, но неограниченной двумерной вселенной. Эта вселенная состоит всего из одного компьютерного экрана, но, когда космический корабль доходит до верхнего края экрана, он не отражается от границы на манер двумерного «Шоу Трумана», а тут же появляется в самом низу. С точки зрения астронавтов, летящих в этом корабле, они совершают бесконечное космическое путешествие. То же происходит и при приближении корабля к левому краю экрана: он не врезается в стенку, а просто появляется на правом краю. Астронавты могут начать замечать повторяющиеся ориентиры, хотя, конечно, в условиях динамической вселенной узнавать одни и те же объекты, мимо которых они пролетают во второй или третий раз, может быть непросто.
На самом деле вселенная «Астероидов» имеет вполне определенную форму. Если допустить существование третьего измерения, в котором эту вселенную можно сложить, то, соединив верхний и нижний края экрана, мы получим цилиндр. Поскольку левый и правый края экрана также смыкаются, можно соединить два конца такого цилиндра и получить объект в форме бублика, который математики называют тором. Поверхность этого трехмерного тела и есть конечная вселенная игры «Астероиды».
Если взять любое конечное трехмерное тело, его двумерная поверхность образует альтернативную вселенную, конечную и не имеющую границ. Еще один пример такой двумерной вселенной дает поверхность сферы. Такие двумерные вселенные – не просто математические игрушки: они дают ключ к путешествиям по поверхности Земли. Многие культуры по всему миру задавались одним и тем же вопросом: бесконечна ли Земля, или же она имеет край, с которого можно упасть? Многие цивилизации представляли Землю в виде диска, окруженного водой, – наподобие мира Трумана.
Идея сферической Земли начала утверждаться лишь у пифагорейцев в V в. до н. э. Исчезновение кораблей за горизонтом, форма тени, отбрасываемой Землей на Луну во время затмений, изменение положения Солнца и звезд по мере продвижения на юг – все это способствовало такому сдвигу мировоззрения. Кругосветная экспедиция, организованная в 1519 г. Фернаном Магелланом (сам он погиб в этом путешествии), окончательно и несомненно доказала, что Земля имеет форму шара.
А как же Вселенная? Имеет ли она форму? Мы находимся примерно в том же положении, что и культуры древности, которые размышляли о форме Земли и хотели узнать, продолжается ли она бесконечно, или имеет край, или же может быть каким-то образом замкнута.
Но как можно сложить трехмерную вселенную, чтобы она имела конечный объем, но не имела краев? Тут может помочь математика, которая позволяет встроить нашу трехмерную Вселенную в пространство, имеющее большее число измерений, и сложить ее так же, как мы сложили мир игры «Астероиды». Хотя физически представить себе такое складывание невозможно, язык математики дает нам уравнения, позволяющие описать такие конечные трехмерные вселенные и, что еще более существенно, изучить их свойства.
Например, мы можем жить в трехмерной версии игры «Астероиды». Возможно, Вселенная, по существу, представляет собой гигантский куб с шестью гранями, подобный нашей игральной кости. Когда космический корабль достигает одной из этих граней, он плавно выходит из кубической вселенной через одну грань и вновь появляется на ее противоположной грани. В «Астероидах» было два замкнутых направления – влево-вправо и вверх-вниз. В трехмерной кубической вселенной должно быть замкнуто и третье направление. Если такой куб поместить в четырехмерную вселенную, его можно сложить, смыкая его грани, и получить четырехмерный бублик, он же тор, трехмерная поверхность которого и есть наша Вселенная.
Но наша Вселенная может иметь и другие формы. Окружность есть конечная двумерная фигура, поверхность которой – это конечная одномерная вселенная. Сфера есть конечная трехмерная фигура, поверхность которой – это конечная двумерная вселенная. При помощи математических уравнений можно построить четырехмерную сферу, поверхность которой будет конечной трехмерной вселенной, – и это будет еще одна возможная модель нашей Вселенной.
Даже если математика дает нам возможные варианты конечных вселенных, не имеющих границ, сможем ли мы когда-нибудь узнать, конечна ли наша Вселенная и какой может быть ее форма? Следует ли нам ожидать появления звездных Магелланов, которые смогут совершить кругосветное путешествие вокруг Вселенной? Учитывая масштабы известной Вселенной, путешествия с непосредственным участием человека кажутся довольно безнадежным способом проверки конечности Вселенной. Но в космосе есть другие путешественники, которые странствовали во Вселенной миллиарды лет и могут кое-что рассказать нам о том, конечна она или нет. Речь идет о фотонах.
Космические Магелланы
Свет – великий путешественник. На нас постоянно падает свет, странствовавший по Вселенной на протяжении многих миллиардов лет. Не может ли часть этого света рассказать нам что-нибудь, что позволит нам догадаться, конечна ли Вселенная? Мы уже поняли, что случится с космическим кораблем, отправившимся в глубины космоса: в такой конечной вселенной он должен в конце концов вернуться в начальную точку своего путешествия, как в 1522 г. вернулись в Севилью корабли Магеллана.
То же может случиться и со светом. Представим себе фотон, покидающий наше Солнце в начале его существования, около 4,5 миллиарда лет назад. Предположим, что мы живем на поверхности четырехмерного бублика, в котором противоположные грани нашей кубической вселенной соединены. Что происходит со светом при приближении к одной из таких граней? Он плавно проходит сквозь нее, возникает на противоположной грани и может продолжать свое путешествие к его исходной точке. Если по пути его ничто не остановит, он может вернуться и попасть в телескоп земного наблюдателя, который впервые обнаружит этот фотон после его долгого путешествия. Что же увидит такой астроном? Да ничего особенного. Свет будет выглядеть так, как будто он был испущен очень удаленной звездой в начале ее существования. Понять, что астроном видит, как выглядело наше Солнце 4,5 миллиарда лет назад, будет очень трудно.
Однако такое положение дает нам возможность попробовать доказать конечность Вселенной, потому что мы можем посмотреть в противоположном направлении и проверить, не видна ли нам похожая картина на противоположной грани. Исследователи во Франции, Польше и США изучали распределение света, возникшего на очень ранних стадиях существования Вселенной в надежде, что разные части составляемой ими картины могут совпасть друг с другом.
Этим ученым показалось, к их немалому удивлению и неменьшему восторгу, что им удалось обнаружить первые признаки совпадения данных. Они начали анализ, который должен был показать, какие именно формы могли дать наблюдаемое распределение длин волн. Согласно полученным результатам, наилучшим кандидатом на роль формы Вселенной, в которой могли появиться такие распределения, был додекаэдр. Это еще одна форма «игральной кости», имеющая 12 пятиугольных граней. Как это ни удивительно, более 2000 лет назад Платон предполагал, что небесный свод, к которому прикреплены звезды, имеет форму не сферы, но именно додекаэдра. Но современная интерпретация предполагает, что, как и в случае сложенного куба, на взаимно противоположных гранях такого додекаэдра пространство смыкается. Интересно отметить, что для совмещения пятиугольников пришлось несколько повернуть их (на 36°). Однако большинству астрономов эти результаты не показались убедительными. Трудно сказать, не являются ли такие соответствия результатом случайного совпадения.
Существует еще один способ получить от света информацию о геометрии Вселенной. Свет может рассказать нам, как Вселенная искривляется. Предположим, наш путешественник, вооруженный телескопом, отправляется из своей деревни через совершенно однородную равнину. Сначала Земля кажется ему плоской, но через некоторое время становится заметной ее кривизна: оглянувшись назад, путешественник уже не видит своей деревни – что-то мешает ему ее увидеть. Если кривизна сохраняется по всей поверхности, то такая поверхность должна быть конечной. Такая кривизна, какую имеет шар, называется положительной кривизной. Плоская поверхность может быть неограниченной, простирающейся бесконечно, но также может быть подобной миру игры «Астероиды», в котором Вселенная экрана оказывается плоской, но конечной. Про плоские поверхности говорят, что они имеют нулевую кривизну. Существует еще один тип кривизны, подобный кривизне седла или чипсов Pringles. Такая фигура изгибается вниз в одном направлении и вверх – в другом. Ее называют отрицательной кривизной в отличие от положительной кривизны поверхности шара. Она создает не конечные, подобные поверхности шара, а бесконечные поверхности.
Двумерная поверхность Земли может быть искривлена в одну или в другую сторону; как выясняется, трехмерное пространство точно так же может иметь кривизну. Измерение этой кривизны может дать нам некоторое представление о том, как может быть сложено пространство. Если подобно Земле Вселенная имеет положительную общую кривизну, то она должна образовывать конечную форму. Если ее кривизна отрицательна, то она должна быть бесконечной. Если же Вселенная плоская, то она может быть бесконечной или конечной, подобно нашему кубическому миру, сомкнутому по противоположным граням.
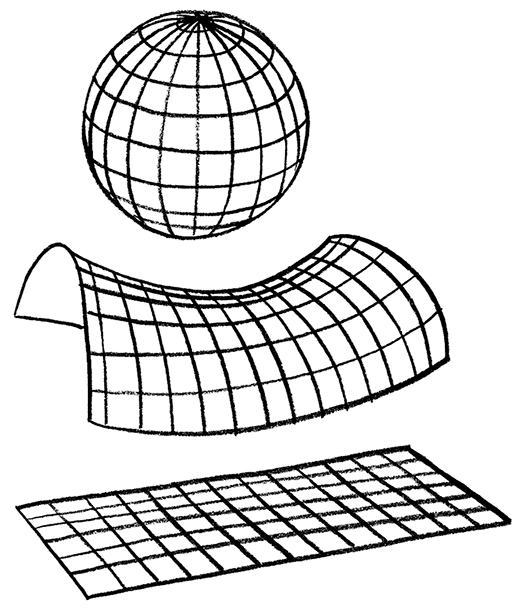
Двумерные поверхности с положительной, отрицательной и нулевой кривизной
Чтобы определить общую кривизну пространства, мы можем исследовать свет, пересекающий его. Что мы видим? Пространство кажется почти что плоским, но трудно сказать, действительно ли оно совершенно плоское, или все-таки существует некая малая кривизна, изгибающая пространство. Различия кажутся такими малыми, что сказать, сможем ли мы когда-нибудь определить эту кривизну с точностью, достаточной, чтобы знать, как изгибается пространство, очень непросто.
Но истинное знание кривизны Вселенной затруднено еще и другим обстоятельством. По большей части наши исследования космоса основаны на предположении о том, что та точка Вселенной, в которой мы находимся, ничем особым не отличается. Эта гипотеза называется принципом Коперника. Когда-то мы считали, что находимся в центре мироздания. Но Коперник покончил с этой идеей. Так что теперь мы полагаем, что окружающая нас Вселенная выглядит приблизительно так же, как и в любом другом месте. Но это может быть и не так. Тот фрагмент Вселенной, который мы видим, вполне может оказаться совершенно особенным.
Представим себе, например, что наш земной путешественник живет на планете, имеющей форму полусферы: у нее совершенно плоское основание, но она неожиданно искривляется и образует половинку шара. Если деревня такого путешественника находится на плоской части, он будет считать, что и вся планета такая же плоская, пока вдруг не обнаружит резкое изменение кривизны. Вселенная может выглядеть таким же образом: она может быть плоской в нашей области, но иметь совершенно другую форму за пределами той части, которую мы можем видеть. Как мы можем быть уверены, что Вселенная столь однородна, как нам кажется?
Итак, вопрос о том, совершает ли свет кругосветные путешествия по конечной Вселенной подобно космической экспедиции Магеллана, все еще остается без ответа. Если это так, мы можем получить шанс узнать, конечна ли Вселенная. А может быть, она изогнута таким образом, что мы сможем выяснить, как именно Вселенная сложена. Конечно, Магеллан путешествовал по статичной планете. Как выяснилось, Вселенная обладает несколько большей динамичностью, чем мы предполагали, и открыл это обстоятельство Хаббл, космический Магеллан, когда он стал анализировать свет, доходящий до нас от звезд удаленных галактик.
Назад: Рубеж четвертый: Бумажная Вселенная
Дальше: 8

