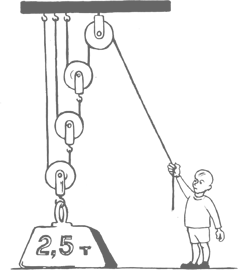
Не самый сильный человек при помощи системы блоков хочет поднять груз весом 2,5 т. При этом, трезво оценивая свои силы, он хотел бы приложить усилие в количестве не более 20 кг – больше ему не выдержать. Какое минимальное число блоков ему потребуется?

1. 8.

2. 32.

3. 125.

Применение блоков, как известно, позволяет с меньшими усилиями поднимать большие грузы. Насколько меньшими? Давайте посчитаем. Берем самую простую систему – двухблочную (см. рисунок – представьте, что там только два блока, неподвижный, прибитый к балке и свободный второй). Сдвинем веревку на l, насколько поднимется груз? Очевидно, на l/2. Работа по подъему груза есть F₁ l = F₂ l/2 (последнее равенство – просто одна из форм записи закона сохранения энергии; здесь F₁ – сила, которую прикладывает человек, F₂ – сила, с которой притягивается к земле груз, т. е. попросту вес груза). Сократив обе стороны равенства на l, получим F₁ = F₂/2. Рассмотрим теперь систему из трех блоков. Рассуждая аналогичным образом, выводим F₁ = F₂/4 и, обобщая на случай n блоков, – F₁ = F₂/2ⁿ⁻¹. Или, переписав эту формулу, 2ⁿ⁻¹ = F₂/F₁ = 2500/20 = 125. Вспоминая, что 128 = 2⁷, а 125 – это почти 128, находим n – 1 = 7, n = 8 – восьми блоков будет достаточно, чтобы поднять груз массой 2,5 т, приложив усилие в 20 кг (и даже немножечко меньшее).