Вы не ожидаете найти математику в паре ваших ботинок. Но поглядите вниз на ваши завязанные шнурки. Эти перевязанные узлы на самом деле могут привести к сложным математическим мыслям.

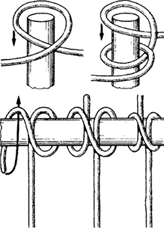
Этот раздел математики известен как теория узлов. Узлы в математике, однако, отличаются от узлов в вашей повседневной жизни одним значимым способом: у них нет свободных концов, то есть они замкнуты. На самом деле, вы можете сделать такой узел самостоятельно. Возьмите кусок веревки – или сваренные спагетти, или лассо – и завяжите обычный узел. Теперь возьмите концы и соедините их с помощью скотча. В итоге у вас может получиться крендель, но в любом случае это будет математический узел!

И хотя отчасти теория узлов хорошо нам знакома, в ней есть свои особенности. В своей книге об узлах Колин Адамс дал следующее определение узлу в математике: «это замкнутая кривая в пространстве, которая не пересекает себя ни в одной точке». Такое определение может натолкнуть вас на мысль о том, какой же узел является простейшим. Таким узлом является простая окружность, такой узел называют «незаузленным». (А еще его называют тривиальным.) Также самыми простыми узлами являются «восьмерка» и «трилистник».

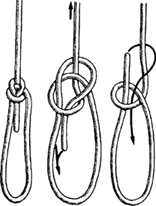
Что конкретно происходит в течение одного дня теоретика, занимающегося узлами? Они обычно стремятся узнать, можно ли развязать тот или иной узел, не разрезая его, или можно ли определить, что узел на самом деле является тривиальным, но в необычной форме. Но теория узлов больше волнует не математиков вовсе. Биологи интересуются теорией узлов из-за ДНК – молекулы, которая кодирует материалы, необходимые для всех живых организмов, – которая иногда может содержать узлы, а они, в свою очередь, могут влиять на то, как информация в молекуле ДНК может интерпретироваться клеточными механизмами организма. Химики также заинтересованы в узлах. Многие из них хотели бы разобраться со сцепленными молекулами, так как в зависимости от узла определенная молекула может совершенным образом поменять свое поведение. (При одной конфигурации вещество может вести себя как масло, а при другой – как гель.) Даже один или два поворота могут иметь существенные последствия.

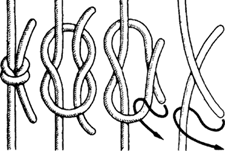
Математик XIX века Питер Гатри Тейт создал классификацию узлов, согласно количеству их пересечений. Он также выдвинул три гипотезы, включая альтернирующие узлы (при проходе такого узла пересечения чередуются «сверху» и «снизу»), хиральные узлы (они не эквивалентны своему зеркальному отражению) и число закрученности (геометрическая величина, которая описывает зацепления в узлах). Все три гипотезы не так давно были доказаны.