Книга: Математические головоломки профессора Стюарта
Назад: Математик, статистик и инженер…
Дальше: Последний лимерик Ферма[28]
Озера Вады
Топология часто контринтуитивна. Это делает ее трудной для освоения, но и интересной. Вот странный топологический факт, имеющий прикладное значение в численном анализе.
Две области на плоскости могут иметь общую границу; представьте себе, к примеру, англо-шотландскую или американо-канадскую границу. Три и больше областей могут иметь общую граничную точку: в американских «Четырех углах» сходятся штаты Аризона, Колорадо, Нью-Мексико и Юта.
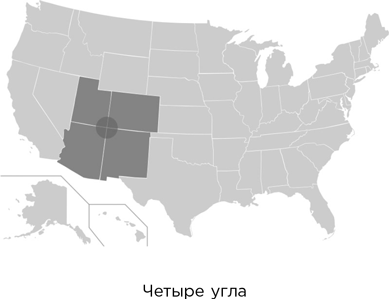
При некоторой изобретательности любое число областей можно организовать так, чтобы они имели две общие граничные точки. Однако представляется невозможным, чтобы три или более областей имели более двух общих граничных точек. Не говоря уже о том, чтобы они имели целиком общую границу.
Однако это возможно.
Во-первых, мы должны точно определить, что такое граничная точка. Предположим, у нас имеется некоторая область на плоскости. Необязательно многоугольник, это может быть любая фигура, в том числе очень сложная – вообще любой набор точек. Говорят, что точка лежит в замыкании области, если любой круг ненулевого (пусть сколь угодно малого) радиуса с центром в этой точке содержит некую точку, лежащую в этой области. Говорят, что точка лежит внутри области, если область включает в себя некоторый круг ненулевого радиуса с центром в этой точке. Тогда граница области состоит из всех точек ее замыкания, не лежащих внутри нее.
Поняли? По существу это то, что лежит на краю, но не внутри.
Для области в виде многоугольника, ограниченной набором отрезков прямых, граница состоит из этих отрезков, так что данное нами определение в этом случае вполне соответствует обычным представлениям. Можно доказать, что три и более многоугольных областей не могут иметь одну и ту же границу. Но для более сложных областей это неверно. В 1917 г. японский математик Кунидзё Ёнеяма опубликовал пример трех областей, имеющих одну и ту же границу. Он сказал, что идею таких областей предложил его учитель Такео Вада. Соответственно, сами области (или аналогичные им) были названы «озерами Вады».
Эти три области строятся шаг за шагом в ходе бесконечного процесса. Начинаем с трех квадратных областей.
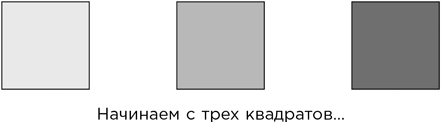
Затем расширяем первую область, добавив дорожку, которая обойдет вокруг всех трех областей. Делаем это так, чтобы каждая точка на границе любого из квадратов лежала близко к дорожке. Проследим также, чтобы дорожка не замыкалась сама на себя, оставив дыру в получившейся области.
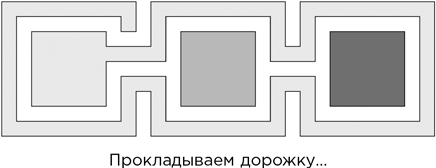
Затем расширяем вторую область, добавляя к ней более узкую тропку, которая обходит вокруг всех трех областей, построенных до сих пор.
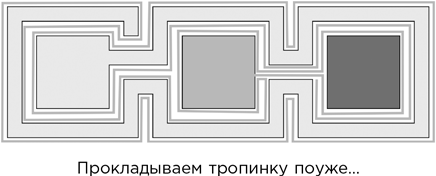
Продолжаем в том же духе, прокладывая еще более узкую тропинку от третьей области. Затем возвращаемся к первой, добавляем к ней еще более узкую тропинку и т. д.
Повторяем это построение бесконечное число раз. Получившиеся области многократно окружены бесконечно сложной сетью бесконечно узких тропинок. Но поскольку с каждым шагом области подходят все ближе ко всему, построенному до того, в конечном итоге все три области имеют одну и ту же (бесконечно сложную) границу.
Первоначально озера Вады были придуманы с целью показать, что топология плоскости не так проста, как можно вообразить. Много лет спустя выяснилось, что такие области возникают сами собой в численных методах решения алгебраических уравнений. К примеру, кубическое уравнение x³ = 1 имеет лишь одно действительное решение x = 1; кроме того, у него есть два комплексных решения 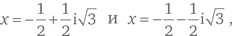 где =√−. Комплексные числа можно представить как точки на плоскости, где число x + iy соответствует точке с координатами (x, y).
где =√−. Комплексные числа можно представить как точки на плоскости, где число x + iy соответствует точке с координатами (x, y).
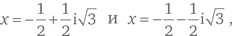 где =√−. Комплексные числа можно представить как точки на плоскости, где число x + iy соответствует точке с координатами (x, y).
где =√−. Комплексные числа можно представить как точки на плоскости, где число x + iy соответствует точке с координатами (x, y).Стандартный метод нахождения численных аппроксимаций начинается со случайно выбранного комплексного числа; затем особым образом вычисляется второе число, а затем процесс повторяется, пока числа не сблизятся. Результат, полученный таким образом, близок к решению. К какому именно из трех решений он близок, зависит от того, где вы начинаете, и происходит это весьма хитроумным образом. Предположим, мы окрасим точки на комплексной плоскости в соответствии с тем, к какому решению они ведут: пусть, к примеру, это будет серый цвет, если решение x = 1, светло-серый, если решение 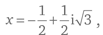 и темно-серый, если решение
и темно-серый, если решение 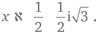 Тогда точки, окрашенные в заданный оттенок серого, обозначат область, и можно доказать, что все три области имеют одну и ту же границу.
Тогда точки, окрашенные в заданный оттенок серого, обозначат область, и можно доказать, что все три области имеют одну и ту же границу.
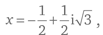 и темно-серый, если решение
и темно-серый, если решение 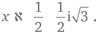 Тогда точки, окрашенные в заданный оттенок серого, обозначат область, и можно доказать, что все три области имеют одну и ту же границу.
Тогда точки, окрашенные в заданный оттенок серого, обозначат область, и можно доказать, что все три области имеют одну и ту же границу.В отличие от построения Вады, области здесь не являются связными: они разбиваются на бесконечное множество отдельных кусочков. Однако поразительно, что области такой сложности возникают естественно в такой фундаментальной задаче численного анализа.

Назад: Математик, статистик и инженер…
Дальше: Последний лимерик Ферма[28]

