Арифметическая последовательность (последовательность чисел с постоянной разницей между соседними членами) называется последовательностью степеней, если второй ее член является полным квадратом, третий – кубом и т. д. То есть k-й член такой арифметической последовательности представляет собой k-ю степень. (Это не накладывает никаких ограничений на первый член последовательности, поскольку любое число есть первая степень самого себя.) К примеру, последовательность 5, 16, 27 имеет длину 3 и шаг 11; кроме того,

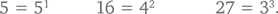
Тривиальный способ получить последовательность степеней длины n состоит в том, чтобы повторить n раз число 2^n!. Это число является одновременно первой степенью, квадратом, кубом и т. д., вплоть до n-й степени. Шаг в этом случае будет равняться 0.

В 2000 г. Джон Робертсон доказал, что, за исключением таких последовательностей, в которых многократно повторяется одно и то же число, – то есть последовательностей с нулевым шагом, – самая длинная возможная последовательность степеней состоит из пяти членов (имеет длину 5). Чтобы получить такую последовательность, возьмите числа 1, 9, 17, 25, 33, образующие арифметическую последовательность с шагом 8, и умножьте каждое из них на 3²⁴5³⁰11²⁴17²⁰. Получившиеся в результате числа тоже образуют арифметическую последовательность с шагом, в восемь раз превосходящим это число. Вот эти числа:

1. 10529630094750052867957659797284314695762718513641400204044879414141178131103515625

2. 94766670852750475811618938175558832261864466622772601836403914727270603179931640625

3. 179003711610750898755280216553833349827966214731903803468762950040400028228759765625

4. 263240752368751321698941494932107867394067962841035005101121985353529453277587890625

5. 347477793126751744642602773310382384960169710950166206733481020666658878326416015625.

Ее шаг равен:

84237040758000422943661278378274517566101748109131201632359035313129425048828125000.

Если обозначить пять членов прогрессии как a₁, a₂, a₃, a₄, a₅, то a₁ есть первая степень самого себя (очевидно);

a₂ = 307841957589849138828884412917083740234375² – квадрат;

a₃ = 5635779747116948576103515625³ – куб;

a₄ = 716288998461106640625⁴ – четвертая степень;

a₅ = 51072299355515625⁵ – пятая степень.

Вот это да!

(Проще всего проверить, что члены последовательности действительно являются заявленными полными степенями, если работать с простыми сомножителями.)