– Ватсап!

– А? Что? Вы это мне, Сомс?

– Сколько раз можно повторять, Ватсап, чтобы вы не приносили журнал The Strand в этот дом!

– Но… как…

– Вы знаете мои методы. Вы нетерпеливо постукивали пальцами, как делаете обычно, пока меня дожидаетесь. При этом вы то и дело поглядывали на свернутую газету, которая торчит у вас из кармана пальто. Газета эта слишком толста для Daily Reporter, хотя именно это название красуется у нее на первой полосе, так что в нее, наверное, завернут какой-то журнал. А поскольку вы по привычке прячете от меня лишь один журнал, сомневаться в его природе не приходится.

– Простите, Сомс, я просто надеялся получить кое-какие сравнительные данные о методах исследования из произведений коллеги… э-э… шарлатана из дома напротив.

– Тьфу! Этот человек – мошенник! Жулик, называющий себя детективом!

Откровенно говоря, временами Сомс бывает невыносим. Если подумать, он почти всегда такой.

– Бывали случаи, когда мне удавалось случайно выудить что-нибудь полезное из скучных творений моего нещадно эксплуатируемого коллеги, Сомс, – возразил я.

– Что, например? – агрессивно вопросил он.

– На меня сильное впечатление произвел такой его аргумент: «Если вы исключите невозможное, то, что останется, каким бы невероятным ни казалось, и будет…

– Ошибкой, – бесцеремонно закончил за меня Сомс. – Если то, что остается, по-настоящему невероятно, значит, вы почти наверняка приняли «по умолчанию» какое-то условие, когда объявляли все другие объяснения невозможными.

Последовательность никогда не значилась в числе добродетелей Сомса.

– Ну, может быть, но…

– Без всяких «но», Ватсап!

– Но ведь в других ситуациях вы соглашались…

– Тьфу! Реальность не бывает невероятной, Ватсап! Она может казаться таковой, но на самом деле ее вероятность составляет 100 %, потому что она уже случилась.

– Ну да, формально это так, но…

– Вот пример. Сегодня утром, когда вы, Ватсап, выходили купить эту лживую газетенку, я принял весьма неожиданного посетителя. Небезызвестного герцога Бамблфортского.

– Главный лондонский щеголь, – сказал я. – Благородный человек безукоризненной честности, образец для всех нас.

– Ну да, ну да. Тем не менее он проинформировал меня… Ну, он рассказал, что в Бамблфорт-холле был обед, на котором эрл Мондеринг, желая развлечь гостей, поставил в ряд десять винных стаканов и наполнил первые пять из них – вот так, – и Сомс продемонстрировал мне этот процесс наглядно, на наших собственных стаканах, наполнив их довольно кислой мадерой, от которой мы как раз решили избавиться. – Затем он предложил гостям переставить стаканы таким образом, чтобы полные чередовались с пустыми.

– Но это очень просто… – начал я.

– Если переставить четыре стакана, то да. Достаточно поменять второй с седьмым и четвертый с девятым. Вот так – (см. рисунок). – Однако эрл просил получить тот же результат, переставив всего два стакана.

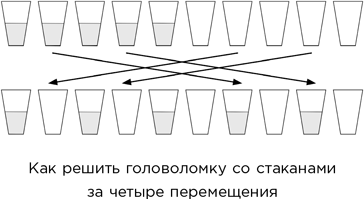
Я сложил пальцы перед собой в жесте глубокого размышления и через мгновение нарисовал грубый набросок первоначального и конечного расположения стаканов.

– Но, Сомс! Четыре названных вами стакана должны оказаться в разных местах! Так что без четырех перестановок не обойтись!

Он кивнул.

– Итак, Ватсап, вы только что исключили невозможное.

– Ну да, ей-богу, так я и сделал, Сомс! Неопровержимо.

Он начал набивать табак в свою трубку.

– И к какому же выводу вы придете, если я скажу, что, по словам герцога Бамблфортского, после того как все гости высказались примерно в таком же духе, эрл Мондеринг продемонстрировал верное решение.

– Я… ну…

– Вы вынуждены признать, что благородный герцог, наследник Британской империи и образец высокого благородства… на самом деле низкий лжец. Поскольку никакого решения не существует, как вы только что доказали.

Мое лицо вытянулось.

– Да, правда, все выглядит именно так… Нет, подождите, возможно, это вы не говорите мне…

– Мой дорогой доктор, я, честно признаюсь, иногда действительно умалчиваю кое-что, исключительно в ваших интересах, но не в данном случае. Даю слово.

– Но тогда… Я шокирован поведением герцога.

– Оставьте, Ватсап. Имейте веру в британский характер.

– Эрл обманывал?

– Нет-нет-нет. Ничего подобного. Вы способны на большее. В этой ситуации может быть и другое вполне прозаическое объяснение, которое вы проглядели. Более того, могу с уверенностью предсказать, что через несколько минут вы сами будете говорить мне, что решение очень простое и что догадаться может даже ребенок.

После этого Сомс рассказал мне, что сделал Мондеринг.

– Ну, здесь даже ребенок дога… – начал я, но вдруг резко остановился. Должен со всей откровенностью признать, что в этот момент я покраснел как рак.