Сомс начал, как одержимый, расхаживать по комнате из угла в угол. Внутренне я громко кричал «Ура!», поскольку ясно видел, что он попался на крючок. Теперь я мог спокойно «вываживать» его, чтобы вывести из черной депрессии, в которую он умудрился впасть, и заодно избавить себя от боливийских погребальных напевов.

– Мы должны действовать систематически, Ватсап! – объявил он.

– Каким образом, Сомс?

– Более систематическим образом, Ватсап, – воцарившееся молчание заставило его поубавить загадочности. – Мы должны составить список небольших чисел, которые можно получить с использованием всего лишь двух единиц. Соединяя их, мы сможем… ну, я уверен, через минуту вы все поймете.

После этого Сомс записал:

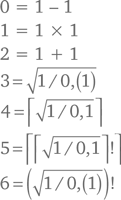
На этом этапе Сомса заклинило.

– Признаюсь, 7 и 8 пока не даются мне, на их местах останутся лакуны, – сказал он. – Но это не важно, позвольте мне продолжить:

9 = 1/0,(1)

10 = 1/0,1

11 = 11.

– Признаюсь, я пока не…

– Будьте уверены, Ватсап, вы все поймете. Предположим, для обобщения, что мы придумали, как выразить 7 и 8 при помощи двух единиц. Тогда в нашем распоряжении окажутся все числа от 0 до 11. Теперь в случае, если некое число n можно выразить при помощи двух единиц, мы получим возможность выразить все числа между n – 11 и n + 11 при помощи всех четырех единиц – просто вычитая или складывая выражения из моего систематического списка.

– Ах, теперь я понял, – сказал я.

– Обычно вам это удается, после того как я вам расскажу, – саркастически отозвался он.

– Тогда позвольте мне кое-что добавить, чтобы показать, что я и правда понял! Поскольку мы знаем, как выразить 24 при помощи двух единиц, к примеру, как мы мгновенно получаем возможность выразить все числа от 24–11 до 24 + 11 при помощи четырех единиц. Это значит, что мы получаем все числа в диапазоне от 13 до 35 включительно.

– Вот именно! Думаю, записывать это не обязательно.

– Да, наверное. Ага! Мы можем пойти еще дальше! Взгляните:

– Да, – ответил он. – Однако, пока энтузиазм не унес вас в несказанные дали, я напомню, что у нас пока нет выражений для 7 и 8 с использованием только двух единиц.

Я принял подобающе удрученный вид. Но затем меня осенила дикая мысль.

– Сомс? – спросил я нерешительно.

– Да?

– Факториалы делают числа больше?

Он раздраженно кивнул.

– А извлечение квадратного корня делает их меньше, так?

– Согласен. Переходите же к делу!

– А операции округления в пол и в потолок вновь делают числа целыми?

Я видел, как на его лице медленно проступает понимание.

– Браво, Ватсап! Да, теперь понятно. Мы знаем, к примеру, как выразить 24 при помощи двух единиц. Следовательно, мы можем также выразить 24! При помощи все тех же двух единиц, а это будет… – его брови сошлись к переносице – 620 448 401 733 239 439 360 000. А корень квадратный из этого числа, – его лицо покраснело от напряжения, пока он производил в уме соответствующие расчеты, – равен 887 516,46; еще раз извлечем квадратный корень, получим 942,08; а еще раз – 30,69.

– Так что мы можем выразить 30 и 31 с использованием всего лишь двух единиц, – сказал я. – А именно:

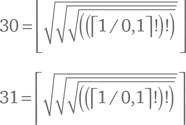
– Ни то ни другое, разумеется, не помогает нам выразить 7 и 8 через две единицы, но если бы мы могли это сделать, то расширили бы диапазон наших чисел до 31 + 1, то есть до 42. И все это говорит о том, что нам, как вы столь убедительно сказали, Сомс, следует действовать систематически. Я предлагаю теперь исследовать многократное извлечение квадратного корня из факториала чисел, которые мы можем выразить через две единицы.

– Согласен! И совершенно очевидно, – заявил тут же Сомс, – что такое выражение для 7 сразу же даст нам выражение для 8.

– Э-э… правда?

– Естественно. Поскольку 7! = 5040, квадратный корень из этого числа равен 70,99, а следующий квадратный корень равен 8,42, мы делаем вывод, что

– Так что не впервые в истории человечества ключом к загадке является число 7! (В этих словах, дорогой читатель, он подчеркивал число 7 восклицательным знаком, а не имел в виду факториал. Пожалуйста, обратите на это внимание, я об этом уже упоминал.)

Сомс нахмурился.

– Я могу сделать это, если использую двойной факториал.

– Вы имеете в виду факториал факториала?

– Нет.

– Субфакториал? Вы пока не объяснили…

– Нет. Двойной факториал – это немного запутанная штука; он равен

n!! = n× (n – 2) × (n – 4) × … × 4 × 2

для четных n и n!! = n× (n – 2) × (n – 4) × … × 3 × 1

для нечетных. Так, к примеру,

6!! = 6 × 4 × 2 = 48.

Корень квадратный из этого числа равен 6,82, а его потолок равен 7.

Я послушно записал:

Но Сомс по-прежнему выглядел недовольным.

– Проблема в том, Ватсап, что при помощи введения все более загадочных и вычурных арифметических функций можно с легкостью выразить вообще любое число. К примеру, мы могли бы воспользоваться арифметикой Пеано.

Я шумно запротестовал:

– Сомс, вы же знаете, что наша хозяйка не устает жаловаться на ваш кларнет. Она никогда не позволит поставить к нам пианино!

– Я говорил о Джузеппе Пеано, так звали итальянского математика и специалиста по логике, Ватсап.

– Откровенно говоря, не такая уж большая разница. Я не уверен, что миссис Сопсудс…

– Тихо! Согласно арифметической аксиоматике Пеано, наследником любого целого числа является число

s (n) = n + 1.

– Так что Пеано вполне мог бы записать:

1 = 1,

2 = s (1),

3 = s (s (1)),

4 = s (s (s (1))),

5 = s (s (s (s (1)))),

и эта последовательность будет продолжаться до бесконечности. В этой системе любое целое число можно выразить при помощи всего одной единицы. Или даже одного нуля, поскольку 1 = s (0). Это слишком тривиально, Ватсап.