Книга: Математические головоломки профессора Стюарта
Назад: Проблема Гольдбаха для нечетных
Дальше: Оптимальная пирамида
Загадки простого числа
В математике есть свои тайны и загадки, и ученые, которые пытаются их разгадать, зачастую похожи на детективов. Они ищут зацепки, занимаются логической дедукцией, делают выводы и ищут доказательства собственной правоты. Как в делах Сомса, важнейший шаг в исследовании – это понять, как и с какого конца начать и какая линия рассуждений может привести к успеху. Во многих случаях мы до сих пор этого не знаем. Возможно, такое заявление звучит как признание собственного невежества, и в какой-то степени это действительно так. Но это заявление означает также, что новая математика до сих пор ждет своего открытия, а значит, эта область науки не вычерпана досуха. Простые числа – богатый источник правдоподобных предположений, о верности или ошибочности которых мы ничего не знаем. Вот некоторые из них. Во всех случаях pn обозначает n-е простое число.
Гипотеза Аго-Джуги
Число p является простым в том, и только том случае, если pBp − 1 + 1 делится на p, где Bk – это k-е число Бернулли (Takashi Agoh, 1990 г.). Если вам по-настоящему интересно, информацию об этих числах можно посмотреть в Интернете. Приведем первые несколько вариантов:
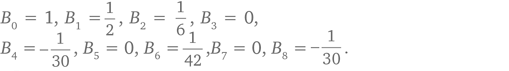
А вот другое, эквивалентное утверждение: число p является простым в том, и только том случае, если
[1p − 1 + 2p − 1 + 3p − 1 + … + (p − 1)p − 1] + 1
делится на p (Guiseppe Giuca, 1950).
Контрпример, если таковой существует, должен иметь по крайней мере 13 800 знаков (David Borwein, Jonathan Borwein, Peter Borwein and Roland Girgensohn, 1996).
Гипотеза Андрики
Если pn – это n-е простое число, то

(Dorin Andrica, 1986).
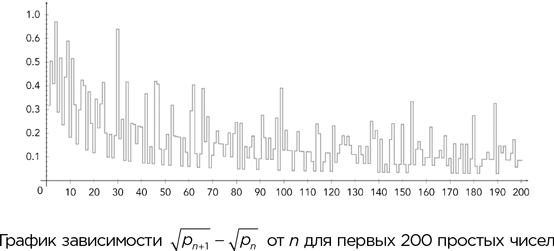
Имран Гори использовал данные о наибольших промежутках между простыми числами, чтобы подтвердить эту гипотезу для n вплоть до 1,3002 × 1016. На рисунке вы можете видеть зависимость √(pn+1) – √pn от n для первых 200 простых чисел. Число 1 располагается в самом верху вертикальной оси, а все остальные пики, показанные на графике, – ниже. Они явно уменьшаются с увеличением n, но мы не можем быть уверены, что на каком-то очень большом n не наблюдается гигантский пик, превосходящий 1. Чтобы данная гипотеза оказалась ошибочной, где-то должен существовать особенно большой промежуток между двумя очень большими последовательными простыми числами. Это представляется весьма маловероятным, но и полностью исключить такой вариант пока невозможно.
Гипотеза Артина о первообразных корнях
Любое целое число a, не равное −1 и не являющееся полным квадратом, есть первообразный корень по модулю бесконечного числа простых чисел. То есть всякое число от 1 до p − 1 есть некая степень a минус некое число, кратное p. Существуют конкретные формулы для количественного соотношения таких простых чисел по мере их увеличения (Emil Artin, 1927).
Гипотеза Брокара
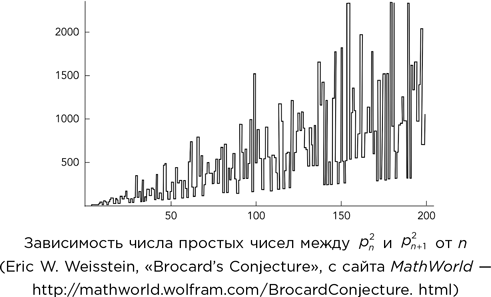
При n > 1 существует по крайней мере четыре простых числа между p² и p²n+1 (Henri Brocard, 1904). Ожидается, что это верно; более того, по идее должны быть верны куда более сильные утверждения.
Гипотеза Крамера
Промежуток pn+1 − pn между последовательными простыми числами для больших n не превосходит (ln pn)² с постоянным коэффициентом (Harald Cramér, 1936).
Крамер доказал аналогичное утверждение, в котором вместо (ln pn)² фигурирует 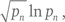 при условии что верна гипотеза Римана – возможно, самая важная нерешенная проблема математики (см. «Кабинет…»).
при условии что верна гипотеза Римана – возможно, самая важная нерешенная проблема математики (см. «Кабинет…»).
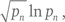 при условии что верна гипотеза Римана – возможно, самая важная нерешенная проблема математики (см. «Кабинет…»).
при условии что верна гипотеза Римана – возможно, самая важная нерешенная проблема математики (см. «Кабинет…»).Гипотеза Фирузбахта
Величина 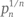 строго уменьшается (Farideh Firoozbakht, 1982 г.). Это означает, что
строго уменьшается (Farideh Firoozbakht, 1982 г.). Это означает, что 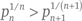 для любого n. Это утверждение верно для всех целых чисел вплоть до 4 × 1018.
для любого n. Это утверждение верно для всех целых чисел вплоть до 4 × 1018.
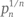 строго уменьшается (Farideh Firoozbakht, 1982 г.). Это означает, что
строго уменьшается (Farideh Firoozbakht, 1982 г.). Это означает, что 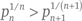 для любого n. Это утверждение верно для всех целых чисел вплоть до 4 × 1018.
для любого n. Это утверждение верно для всех целых чисел вплоть до 4 × 1018.Первая гипотеза Харди – Литтлвуда
Пусть π2 (x) обозначает число простых чисел p ≤ x, таких, что p + 2 также простое число. Определим постоянную простых чисел-близнецов
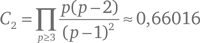
(где символ П указывает на произведение по всем простым числам p ≥ 3). Тогда гипотеза заключается в том, что
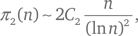
где знак ~ означает, что данное отношение стремится к 1 по мере того, как n становится сколь угодно большим (Godfrey Harold Hardy and John Edensor Littlewood, 1923).
Существует также вторая гипотеза Харди – Литтлвуда (см. ниже).
Гипотеза Гилбрейта
Начнем с простых чисел
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, …
и вычислим разницу между соседними членами последовательности:
1, 2, 2, 4, 2, 4, 2, 4, 6, 2, …
Повторим те же вычисления для новой последовательности, не обращая внимания на знак, и продолжим в том же духе. Пять первых последовательностей будут выглядеть следующим образом:
1, 0, 2, 2, 2, 2, 2, 2, 4, …
1, 2, 0, 0, 0, 0, 0, 2, …
1, 2, 0, 0, 0, 0, 2, …
1, 2, 0, 0, 0, 2, …
1, 2, 0, 0, 2, …
Гилбрейт и Прот предположили, что первым членом каждой из этих последовательностей всегда будет 1, сколько бы раз мы ни повторяли процедуру (Norman Gilbreath, 1958, François Proth, 1978).
В 1993 г. Эндрю Одлизко проверил эту гипотезу для первых 3,4 × 1011 последовательностей.
Гипотеза Гольдбаха для четных чисел
Всякое четное целое число, большее 2, можно выразить как сумму двух простых чисел (Christian Goldbach, 1742).
Т. Оливейра-и-Силва проверил эту гипотезу на компьютере для n ≤ 1,609 × 1018.
Гипотеза Гримма
Каждому элементу множества последовательных составных чисел можно поставить в соответствие отдельное простое число, которое является его делителем (C. A. Grimm, 1969).
К примеру, если взять составные числа 32, 33, 34, 35, 36, то им можно поставить в соответствие простые числа 2, 11, 17, 5, 3.
Четвертая проблема Ландау
В 1912 г. Эдмунд Ландау перечислил четыре фундаментальные проблемы, связанные с простыми числами и известные в настоящее время как проблемы Ландау. Первые три – это гипотеза Гольдбаха (см. выше), гипотеза о простых числах-близнецах (см. ниже) и гипотеза Лежандра (см. ниже). Четвертая проблема выглядит так: существует ли бесконечно много простых чисел p, таких что p − 1 является полным квадратом? То есть p = x² + 1 для целого x.
Вот первые несколько таких чисел: 2, 5, 17, 37, 101, 197, 257, 401, 577, 677, 1297, 3137, 4357, 5477, 7057, 8101, 8837, 12 101, 13 457, 14 401 и 15 377. А вот пример побольше (но ни в коем случае не самый большой):
p = 1, 524, 157, 875, 323, 883, 675, 049, 535, 156, 256, 668, 194, 500, 533, 455, 762, 536, 198, 787, 501, 905, 199, 875, 019, 052, 101x = 1, 234, 567, 890, 123, 456, 789, 012, 345, 678, 901, 234, 567, 890.
В 1997 г. Джон Фридлендер и Хенрик Иванец доказали, что существует бесконечно много простых чисел вида x2 + y4 для целых x, y. Первые из этого ряда: 2, 5, 17, 37, 41, 97, 101, 137, 181, 197, 241, 257, 277, 281, 337, 401 и 457. Иванец доказал, что существует бесконечно много чисел вида x² + 1, имеющих не более двух простых множителей.
Близко, но не то.
Гипотеза Лежандра
Адриан-Мари Лежандр предположил, что для любого положительного n существует простое число, лежащее между n² и (n + 1)². Это утверждение могло бы быть следствием из гипотезы Андрики (см. выше) и гипотезы Опперманна (см. ниже). Из гипотезы Крамера (см. выше) следует, что гипотеза Лежандра верна для всех достаточно больших чисел. Известно, что она верна вплоть до 1018.
Гипотеза Лемуана, или гипотеза Леви
Все нечетные целые числа, большие 5, могут быть представлены как сумма нечетного простого числа и удвоенного простого числа (Émile Lemoine, 1894, Hyman Levy, 1963).
Д. Корбитт подтвердил эту гипотезу вплоть до 109.
Гипотезы Мерсенна
В 1644 г. Марен Мерсенн объявил, что числа 2n – 1 являются простыми для n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 и 257 и составными для всех остальных положительных целых n<257. Позже было показано, что Мерсенн допустил пять ошибок: n = 67 и 257 дают составные числа, а n = 61, 89, 107 дают простые. Гипотеза Мерсенна привела к созданию новой гипотезы Мерсенна и гипотезы Ленстры – Померанца – Вагстаффа, которые значатся в нашем перечне следующими.
Новая гипотеза Мерсенна, или гипотеза Бейтмана– Селфриджа – Вагстаффа
Для любого нечетного p если выполняются любые два из следующих условий, то выполняется и третье:
1. p = 2k ± 1 или p = 4k ± 3 для некоторого натурального числа k;
2. число 2p − 1 – простое (простое Мерсенна);
3. число (2p + 1)/3 – простое (простое Вагстаффа).
(Paul Bateman, John Selfridge and Samuel Wagstaff Jr., 1989)
Гипотеза Ленстры – Померанца – Вагстаффа
Существует бесконечное число простых Мерсенна, причем число простых Мерсенна, меньших x, приблизительно равно eγ ln ln x/ln 2, где γ – постоянная Эйлера, приблизительно равная 0,577 (Hendrik Lenstra, Carl Pomerance and Samuel Wagstaff Jr., не опубликовано).
Гипотеза Опперманна
Для любого целого числа n>1 существует по крайней мере одно простое число между n (n – 1) и n² и по крайней мере еще одно простое число между n² и n (n + 1) (Ludvig Henrik Ferdinand Oppermann, 1882).
Гипотеза Полиньяка
Для любого положительного четного n существует бесконечное число пар последовательных простых чисел с разницей в n (Alphonsede Polignac, 1849).
Для n = 2 это утверждение соответствует гипотезе о простых числах-близнецах (см. ниже). Для n = 4 она означает, что существует бесконечно много пар «двоюродных простых чисел» (p, p + 4). Для n = 6 она означает, что существует бесконечно много пар простых чисел (p, p + 6), известных как sexy (от латинского названия числа 6); при этом между числами p и p + 6 простых чисел нет.
Гипотеза Редмонда – Суня
Всякий интервал [xm, yn] (то есть любое множество чисел от xm до yn) содержит по крайней мере одно простое число, за исключением [2³, 3²], [5², 3³], [25, 6²], [11², 5³], [37, 13³], [55, 56²], [181², 215], [43³, 282²], [46³, 312²], [22434², 555] (Stephen Redmond and Zhi-Wei Sun, 2006).
Эта гипотеза подтверждена для всех интервалов [xm, yn] до 10¹².
Вторая гипотеза Харди – Литтлвуда
Если π (x) есть число простых чисел вплоть до x, включая x, то π (x + y) ≤ π (x) + π (y) для x, y ≥ 2 (Godfry Harold Hardy and John Littlewood, 1923).
Существуют технические соображения, согласно которым можно ожидать, что это предположение окажется ложным, но первое нарушение возникнет, скорее всего, при очень больших величинах x, вероятно, больших, чем 1,5 × 10174, но меньших, чем 2,2 × 101198.
Гипотеза о простых числах-близнецах
Существует бесконечно много простых чисел p, таких, что число p + 2 тоже простое.
25 декабря 2011 г. PrimeGrid – «проект распределенных вычислений», в котором используются свободные ресурсы на компьютерах добровольцев, пожелавших принять в нем участие, объявил наибольшую известную на сегодняшний день пару простых чисел-близнецов:
3 756 801 695 685 × 2666 669 ± 1.
Каждое из этих чисел содержит 200 700 знаков.
В интервале до 1018 содержится 808 675 888 577 436 пар простых чисел-близнецов.
Назад: Проблема Гольдбаха для нечетных
Дальше: Оптимальная пирамида

