Треугольные числа 1, 3, 6, 10, 15 и т. д. определяются сложением последовательных чисел, начиная с 1:

1 = 1;

1 + 2 = 3;

1 + 2 + 3 = 6;

1 + 2 + 3 + 4 = 10;

1 + 2 + 3 + 4 + 5 = 15

и т. д. Для таких чисел существует формула:

1 + 2 + 3 + … + n = n (n + 1)/2.

Чтобы доказать ее, можно, в частности, записать сумму дважды, примерно так:

1 + 2 + 3 + 4 + 5;

5 + 4 + 3 + 2 + 1.

Из этой записи видно, что числа в вертикальных столбцах при сложении дают одно и то же, в данном случае 6. Поэтому удвоенная сумма равна 6 × 5 = 30, а сумма равна 15. Если проделать то же самое с числами от 1 до 100, все получится примерно так же: будет 100 колонок, дающих при сложении сумму 101, так что сумма первых 100 чисел должна составлять половину от 100 × 101, то есть 5050. В более общем случае при сложении первых n чисел мы получаем половину от n (n + 1). Формула готова.

Существует формула и для суммы квадратов, но более сложная:

1 + 4 + 9 + … + n² = n (n + 1) (2n + 1)/6.

А вот с кубами происходит нечто поразительное:

1³ = 1;

1³ + 2³ = 9;

1³ + 2³ + 3³ =36;

1³ + 2³ + 3³ + 4³ = 100;

1³ + 2³ + 3³ + 4³ + 5³ = 225.

Результаты здесь – квадраты соответствующих треугольных чисел.

Почему в результате суммирования кубов получаются квадраты? Можно найти формулу и доказать таким способом все, что нам нужно, но существует очень аккуратное наглядное доказательство того, что 1³ + 2³ + 3³ + … + n³ = (1 + 2 + 3 + … + n)², для которого не нужны никакие формулы.

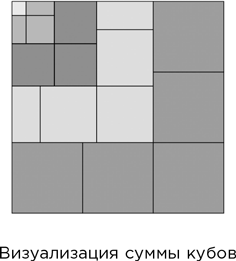
На рисунке показан один квадрат со стороной 1, два квадрата со стороной 2 (образующие куб 2 × 2 × 2), 3 квадрата со стороной 3 (куб 3 × 3 × 3) и т. д. Так что суммарная площадь этой фигуры представляет собой сумму последовательных кубов. Следуя вдоль одной из сторон (к примеру, верхней), видим 1 + 2 + 3 + 4 + 5, то есть сумму последовательных чисел. Но площадь квадрата равна квадрату его стороны. Готово!

Если вам непременно нужна формула, то мы знаем, что (1 + 2 + 3 + … + n) = n (n + 1)/2, а возведение в квадрат дает 1³ + 2³ + 3³ + … + n³ = n² (n + 1)²/4.