Современные читатели узнают в головоломке Ватсапа один из вариантов судоку. (На случай, если вы только что вернулись из сорокалетней экспедиции на Проксиму Центавра, поясню: это квадрат 9 × 9, разделенный на 9 блоков 3 × 3, причем в некоторых клетках заранее проставлены цифры. Нужно заполнить остальные клетки таким образом, чтобы в каждой строке, каждом столбце и каждом блоке содержались все цифры от 1 до 9.)

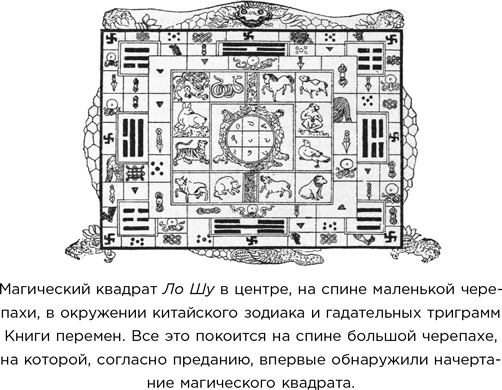
Похожие, но существенно различающиеся головоломки известны давно и имеют долгую историю, восходящую к китайцу Ло Шу и его магическому квадрату, который он будто бы увидел на спине черепахи примерно в 2100 г. до н. э. Книга «Математические и физические развлечения» Жака Озанама, написанная в 1725 г., включала в себя головоломку на тему карточной игры, чуть более близкую к судоку. Возьмите 16 фигурных карт (это туз, король, дама и валет) и выложите их квадратом так, чтобы в каждом ряду и каждом столбце содержались карты всех мастей и достоинств. Кэтлин Оллереншоу показала, что существует 1152 решения этой задачи, которые сводятся всего лишь к двум принципиально разным вариантам, если считать, что два решения совпадают, если одно может быть получено из другого перестановкой мастей или достоинств. Существует 24 × 24 = 576 способов сделать это с любым заданным решением, а 1152/576 = 2.

В 1782 г. Эйлер опубликовал задачу о 36 офицерах: можно ли построить офицеров шести полков, в каждом из которых по шесть офицеров разных рангов, в каре (то есть квадратом) 6 × 6 таким образом, чтобы в каждой шеренге и в каждой колонне присутствовали офицеры всех рангов из всех полков? Подобные расстановки получили название греко-латинских квадратов, потому что латинские (A, B, C, …) и греческие (α, β, γ, …) буквы можно использовать для обозначения рангов и полковой принадлежности. Эйлер нашел методы построения греко-латинских квадратов, порядок которых (то есть размер квадрата) является нечетным числом или имеет двойную четность, то есть кратен четырем.

Эйлер предположил, что для порядка, выражаемого удвоенным нечетным числом, таких квадратов не существует. Для порядка 2 это очевидно, а в 1901 г. Гастон Тарри доказал это для порядка 6. Однако в 1959 г. Радж Чандра Бозе и Шарадчандра Шанкар Шриханде сумели при помощи компьютера отыскать греко-латинский квадрат порядка 22, а Эрнест Паркер нашел такой квадрат порядка 10. После этого все трое доказали, что гипотеза Эйлера неверна для всех удвоенных нечетных чисел, больших или равных 10.

Квадратные таблицы размером n × n, такие, что каждая строка и каждый столбец содержит все числа от 1 до n (каждое, понятно, по одному разу), получили известность как латинские квадраты, а греко-латинские квадраты были переименованы в ортогональные латинские квадраты. Эти темы входят в область математики, которую называют комбинаторикой, и применяются в области коммуникаций, в экспериментальном дизайне и при составлении расписаний всевозможных соревнований.

Полный шаблон судоку – это латинский квадрат, но в головоломке присутствуют и дополнительные условия по отношению к внутренним блокам 3 × 3. В 1892 г. французская газета Le Siècle напечатала на своих страницах головоломку, в которой из магического квадрата были удалены некоторые числа, и читатели должны были их восстановить. La France вплотную подошла к изобретению судоку, так как в ее магических квадратах использовались только цифры от 1 до 9. В решениях, кстати говоря, каждый из блоков 3 × 3 тоже содержал все девять цифр, но явно об этом нигде не говорилось.

Судоку в его современной форме предложил, вероятно, Говард Гарнс, а опубликована первая головоломка была анонимно в Dell Magazines в 1979 г. под названием «числовая площадь». В 1986 г. японская компания Nikoli публиковала такие головоломки в Японии под не слишком удобоваримым и заметным названием suji wa dokushin ni kagiru («все цифры по одному разу»). Позже название сократили до su doku. Газета The Times начала публиковать головоломки судоку в Великобритании в 2004 г., после того как Уэйн Гулд, написавший компьютерную программу, способную отыскивать решения практически мгновенно, обратился в редакцию с предложением о сотрудничестве. В 2005 г. судоку во всем мире стали модным увлечением.