Мы используем не то среднее. Нам нужно среднее гармоническое (что это такое, объясняется ниже), а не среднее арифметическое.

Обычно мы определяем «среднюю скорость» какого-то путешествия как полное проделанное расстояние, деленное на полное затраченное время. Если путешествие разбито на несколько этапов, то средняя скорость, как правило, не является средним арифметическим скоростей на этих отрезках. Если отрезки преодолеваются за равное время, среднее арифметическое годится, но если они имеют равную длину (как и обстоит дело в нашем случае), то это не так.

Сначала рассмотрим случай с равными временны́ми отрезками. Предположим, что машина едет со скоростью a время t, а затем со скоростью b то же время t. Полное расстояние, равное at + bt, занимает время 2t. Поэтому средняя скорость равна (at + bt)/2t, что равно (a + b)/2, то есть среднему арифметическому скоростей.

Теперь возьмем случай с равными расстояниями. Машина проезжает расстояние d на скорости a за время r. Затем она снова проезжает расстояние d, на этот раз со скоростью b за время s. Полное расстояние равно 2d, полное время равно r + s. Чтобы выразить это через скорости a и b, заметим, что d = ar = bs. Таким образом, r = d/a, а s = d/b. Тогда средняя скорость равна

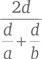
Это выражение упрощается до 2ab / (a + b), что соответствует гармоническому среднему a и b. Эта величина обратна среднему арифметическому величин, обратных a и b, где под величиной, обратной x, подразумевается 1/x. Причина в том, что время, затраченное на дорогу, пропорционально величине, обратной скорости.