Книга: Математические головоломки профессора Стюарта
Назад: Блинные числа
Дальше: Загадка гусиного клина
Дело о таинственном колесе 
– Диаметр колеса, разумеется, равен 58 дюймам, – сказал Сомс. – Это элементарное следствие из теоремы Пифагора.
Я обдумал это заявление. Следует отметить, что у меня есть некоторый опыт в области геометрии и алгебры.
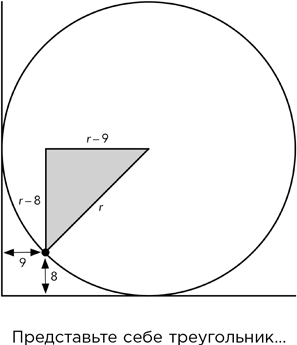
– Позвольте мне попробовать, Сомс. Я считаю, что радиус колеса равен r. Заштрихованный треугольник на вашем чертеже – прямоугольный, его гипотенуза равна r, а две другие стороны равны r – 8 и r – 9. Таким образом, мы, как вы и намекали, можем применить теорему Пифагора и получить
(r – 8)² + (r – 9)² = r².
То есть
r² – 34r + 145 = 0.
Я уставился на записанные символы, временно остановившись.
– Квадратный двучлен раскладывается на множители, Ватсап:
(r – 29) (r – 5) = 0.
– Да, точно! И это означает, что его решения равны r = 29 и r = 5.
– Да. Но вы должны помнить, что диаметр колеса равен 2r, то есть 58 или 10. Однако решение 10 дюймов нам не подходит, поскольку диаметр тележного колеса не может быть меньше 20 дюймов. Значит, остается только…
– …58 дюймов, – закончил я за него.
Назад: Блинные числа
Дальше: Загадка гусиного клина

