Гаусс доказал, что 17-угольник можно построить, если вы умеете строить отрезки длиной

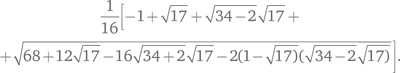
Поскольку квадратный корень всегда можно построить, это вполне эффективно решает задачу. Другие математики нашли более очевидные построения. Ульрих фон Гугенин опубликовал первое из них в 1803 г., а Г. Ричмонд в 1893 г. нашел более простое. На рис. 54 возьмем два перпендикулярных радиуса AOP₀ и BOC окружности. Пусть OJ = 1/4 OB, а угол OJE = 1/4 OJP₀. Найдем F, такое, что угол EJF равен 45°. Построим окружность с диаметром FP₀; она пересекается с OB в точке K. Проведем через K окружность с центром в точке E; она пересечет AP₀ в точках G и H. Построим в этих точках перпендикуляры к AP₀, назовем их HP₃ и GP₅. Тогда P₀, P₃, P₅ представляют собой соответственно нулевую, третью и пятую вершины правильного 17-угольника. Теперь несложно построить и остальные вершины.