Глоссарий
Алгебраическое целое число. Комплексное число, удовлетворяющее полиномиальному уравнению с целыми коэффициентами и коэффициентом при наибольшей степени 1. К примеру, i√2, удовлетворяющее уравнению x² + 2 = 0.
Алгебраическое число. Комплексное число, удовлетворяющее полиномиальному уравнению с целыми коэффициентами или эквивалентными рациональными коэффициентами. К примеру, i√2/3 удовлетворяет уравнению или эквивалентно 9x² + 2 = 0.
Алгебраическое многообразие. Множество в многомерном пространстве, определяемое системой алгебраических уравнений.
Алгоритм. Определенная процедура решения задачи, гарантированно приводящая к ответу.
Арифметическая прогрессия. Последовательность чисел, в которой каждое следующее число равно предыдущему плюс некая постоянная величина, разность прогрессии. Пример такой последовательности: 2, 5, 8, 11, 14… с разностью 3.
Асимптотический. Две величины, определенные через одну переменную, асимптотически равны, если по мере произвольного роста переменной их отношение все сильнее приближается к 1.
Бозон Хиггса. Элементарная частица, существование которой объясняет, почему все частицы обладают массой. О его открытии на Большом адронном коллайдере было объявлено в июле 2012 г.
Вектор. В механике величина, которая характеризуется как размером, так и направлением.
Верхняя граница. Конкретное число, гарантированно большее, чем некая искомая величина.
Вихрь. Жидкость, кружащаяся в водовороте. Может быть любого размера, в том числе очень маленького.
Волна. Возмущение, которое движется сквозь среду — твердое тело, жидкость или газ, не оставляя после себя в среде никаких постоянных изменений.
Вращение (поворот). На плоскости: преобразование, при котором все точки сдвигаются на один и тот же угол вокруг фиксированного центра. В пространстве: преобразование, при котором все точки сдвигаются на один и тот же угол вокруг фиксированной прямой — оси вращения.
Время разрушения решения. Время, после которого решение дифференциального уравнения прекращает существовать.
Гомология (группа). Топологический инвариант пространства, определенный замкнутыми петлями. Две петли гомологичны, если их разность представляет собой границу топологического диска.
Гомотопия (группа). Топологический инвариант пространства, определенный замкнутыми петлями. Две петли гомотопичны, если любая из них может быть непрерывно преобразована во вторую.
Гранецентрированная кубическая решетка. Повторяющаяся в пространстве совокупность точек. Кубики ставятся рядами и один на другой, образуя как бы трехмерную шахматную доску, а затем берутся их вершины и центры всех шести граней (см. рис. 17, 19).
Граница. Край определенной области.
Группа. Абстрактная алгебраическая структура, включающая в себя множество и правило комбинирования двух любых элементов множества, соответствующее трем условиям: в нем выполняется сочетательный закон, существует единичный элемент и каждому элементу соответствует обратный элемент.
Действительное число. Любое число, которое может быть выражено десятичной дробью, возможно, бесконечной. Пример: π = 3,1415926535897932385…
Дзета-функция. Комплексная функция, введенная Риманом и представляющая простые числа аналитически. Определяется рядом
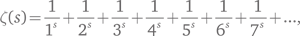
который сходится, если действительная часть s больше единицы. Это определение может быть расширено на все комплексные s при помощи процесса, известного как аналитическое продолжение.
Динамическая система. Любая система, которая изменяется во времени по определенным правилам. К примеру, движение планет в Солнечной системе.
Диофантово уравнение. Уравнение, решения которого должны быть рациональными числами.
Диск (топологический). Область на поверхности, которую можно непрерывно преобразовывать в окружность вместе с тем, что у нее внутри.
Дифференциальное уравнение. Уравнение, в котором функция соотносится со скоростью ее изменения.
Дифференциальное уравнение в частных производных. Дифференциальное уравнение, в котором фигурируют скорости изменения некой функции по отношению к двум или более различным переменным (часто это пространство и время).
Додекаэдр. Многогранник, гранями которого являются 12 правильных пятиугольников (см. рис. 38).
Двойственная сеть. Сеть, полученная из данной сети. Чтобы получить ее, каждую область первоначальной сети следует заменить точкой и соединить эти точки ребрами, если соответствующие области граничат (см. рис. 10).
Единственность разложения на простые множители. Свойство, согласно которому любое число может быть записано как произведение простых множителей единственным способом с точностью до порядка записи множителей. Это верно для целых чисел, но не всегда верно в более общих алгебраических системах.
Идеальное число. Число, которое не входит в данную систему алгебраических чисел, но связано с этой системой так, что восстанавливает единственность разложения на простые множители в случаях, когда это свойство нарушается. В современной алгебре заменен идеалом — особым подмножеством той же системы.
Импульс. Произведение массы на скорость.
Индукция. Общий метод доказательства теорем о натуральных числах. Если какое-то свойство истинно для 0 и из его истинности для любого натурального n следует его истинность для n + 1, это свойство истинно для всех натуральных чисел.
Интеграл. Операция исчисления, при которой, по существу, складывается очень большое количество очень маленьких составляющих. Интеграл функции равен площади под ее графиком.
Иррациональное число. Действительное число, которое не является рациональным, т. е. не может быть записано в виде p/q, где p и q — целые числа и q ≠ 0. Примерами могут служить √2 и π.
Калибровочная симметрия. Группа местных симметрий системы уравнений: преобразования переменных в разных точках пространства может быть различными, но, если обеспечить уравнениям компенсирующее изменение с разумным физическим обоснованием, любое решение системы остается решением.
Калибровочная теория. Квантовая теория поля с группой калибровочных симметрий.
Квадрат. Результат умножения числа на самое себя. К примеру, квадрат 7 равен 7 × 7 = 49, обозначается 7².
Квадратное уравнение. Любое уравнение ax² + bx + c = 0, где x — неизвестное, а a, b, c — константы.
Квантовая теория поля. Квантовомеханическая теория величины, которая пронизывает пространство и может иметь (и обычно имеет) разные значения в разных его местах.
Квантово-волновая функция. Математическая функция, определяющая свойства квантовой системы.
Класс E. Алгоритм, время работы которого для входа размера n пропорционально n-й степени некоей постоянной величины.
Класс P. Алгоритм, время работы которого пропорционально некоей постоянной степени размера входа.
Класс не-P. Не класс P.
Класс NP. Задача, для которой предлагаемое решение может быть проверено (но необязательно найдено) при помощи алгоритма класса P.
Класс Ходжа. Когомологический класс циклов на алгебраическом многообразии с особыми аналитическими свойствами.
Когомологическая группа. Абстрактная алгебраическая структура, связанная с топологическим пространством, аналогичная гомологической группе, но «двойственная» ей.
Комплексный анализ. Анализ — логически строгие вычисления, осуществляемые при помощи комплексных функций комплексного переменного.
Комплексное число. Число вида a + bi, где i — корень квадратный из −1, а a и b — действительные числа.
Конгруэнтное число. Число, которое может быть общей разностью последовательности трех квадратов рациональных чисел.
Контрпример. Пример, опровергающий некое утверждение. Так, 9 может служить контрпримером к утверждению «все нечетные числа простые».
Корень из единицы. Комплексное число ζ, некоторая степень которого ζk = 1 (см. рис. 7 и прим. 33).
Коэффициент. В многочлене, таком как 6x³ − 5x² + 4x − 7, коэффициентами являются числа 6, −5, 4, −7, на которые домножаются различные степени x.
Координата. Одно из чисел в списке, определяющем положение точки на плоскости или в пространстве.
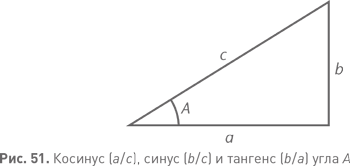
Косинус. Тригонометрическая функция угла, определяемая как cos A = a/c на рис. 51.
Кривизна. Мера искривления пространства в окрестности данной точки. Сфера обладает положительной кривизной, плоскость — нулевой кривизной, а седловидная поверхность — отрицательной.
Круговое число, круговое целое число. Сумма степеней комплексного корня из единицы с рациональными либо целыми коэффициентами.
Куб. Число, умноженное на себя и еще раз на себя. К примеру, куб 7 равен 7 × 7 × 7 = 343. Обычно записывается как 7³.
Кубическое уравнение. Любое уравнение вида ax³ + bx² + cx + d = 0, где x — неизвестное, а a, b, c, d — постоянные.
L-функция Дирихле. Обобщение дзета-функции Римана.
Логарифм. Натуральный логарифм x (обозначается log x) — это степень, в которую нужно возвести e (= 2,71828…), чтобы получить x. Иными словами, elog x = x.
Логарифмический интеграл. Функция 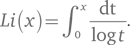
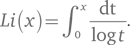
Максимум. Наибольшее значение чего-либо.
Минимальный контрпример. Математический объект, не обладающий неким желаемым свойством, причем в определенном смысле минимально возможный такой объект. К примеру, карта, которую невозможно раскрасить в четыре краски и состоящая притом из минимального числа областей, при котором это невозможно. Минимальные контрпримеры часто бывают гипотетическими, а цель математика при этом — доказать, что их не существует.
Минимум. Наименьшее значение чего-либо.
Многогранник. Тело, граница которого состоит из конечного числа многоугольников.
Многообразие. Многомерный аналог гладкой поверхности; форма в пространстве, определенная системой полиномиальных уравнений.
Многоугольник. Плоская фигура, граница которой состоит из конечного числа отрезков прямых.
Многочлен. Алгебраическое выражение, к примеру 6x³− 5x² + 4x − 7, в котором различные степени переменной x умножаются на константы и складываются.
Множество. Набор (математических) объектов. К примеру, множество целых чисел.
Модульная арифметика. Арифметическая система, в которой числа, кратные некоему заданному числу, называемому модулем, рассматриваются как равные нулю.
Момент импульса. Мера вращения тела.
Натуральное число. Любое из чисел 1, 2, 3…
Неевклидова геометрия. Альтернатива геометрии Евклида, в которой все обычные свойства точек и прямых сохраняются, за исключением допущения о существовании единственной прямой, параллельной данной и проходящей через заданную точку. Существует две разновидности неевклидовой геометрии: эллиптическая и гиперболическая.
Непрерывное преобразование. Преобразование пространства, при котором точки, расположенные очень близко друг к другу, не растаскиваются на большое расстояние.
Неприводимый многочлен. Многочлен, который нельзя получить при перемножении двух многочленов меньших степеней.
Неустойчивое состояние. Состояние динамической системы, к которому она не может вернуться после небольшого возмущения.
Неустранимая конфигурация. Элемент списка подсетей, по крайней мере одна из которых должна обязательно присутствовать в любой сети на плоскости.
NP-полная задача. Конкретная задача NP-класса, такая что если для ее решения существует алгоритм класса P, то любая задача класса NP может быть решена при помощи алгоритма класса P.
Нуль (функции). Если f — функция, то x является нулем f, если f (x) = 0.
Общая теория относительности. Теория гравитации Эйнштейна, в которой сила тяготения рассматривается как кривизна пространства-времени.
Оператор. Особый вид функции A, который при приложении к вектору v дает другой вектор Av. Должен удовлетворять условиям линейности: A(v + w) = Av + Aw и A (av) = aA(v) для любой постоянной a.
Оптимизация. Нахождение максимума или минимума некой функции.
Ось вращения. Фиксированная прямая, вокруг которой вращаются объекты.
Отношение. Отношение двух чисел a и b есть a/b.
Параллельный перенос. Преобразование пространства, при котором все точки сдвигаются в одном и том же направлении на одно и то же расстояние.
Переменная. Величина, которая может принимать любое значение в определенных пределах.
Периодичность. Бесконечная повторяемость одного и того же поведения.
Петля. Замкнутая кривая в топологическом пространстве.
Пифагорова тройка. Три натуральных числа a, b, c, такие что a² + b² = c². К примеру, a = 3, b = 4, c = 5. По теореме Пифагора такие числа образуют стороны прямоугольного треугольника.
Плоский тор. Тор, полученный отождествлением противоположных сторон квадрата, естественная геометрия которого имеет нулевую кривизну (см. рис. 12).
Поверхность. Форма в пространстве, полученная путем объединения областей, топологически эквивалентных внутренней части круга. Примеры: сфера и тор.
Показатель степени. Число, показывающее, в какую степень возводится переменная x. Для x7 показатель степени −7.
Поле скоростей. Функция, определяющая вектор скорости в каждой точке пространства. К примеру, в потоке жидкости вектор скорости может быть определен в каждой точке, и, как правило, в разных точках он разный.
Порядок кривой. Число раз, которые кривая оборачивается против часовой стрелки вокруг выбранной точки.
Последовательность. Список чисел в определенном порядке. К примеру, последовательность 1, 2, 4, 8, 16… степеней двойки.
Постоянная Эйлера. Специальное число, обозначаемое γ и приблизительно равное 0,57721 (см. прим. 41).
Построение при помощи линейки и циркуля. Любое геометрическое построение, которое можно реализовать при помощи только неразмеченной линейки и циркуля-измерителя (строго говоря, двух измерителей).
Поток Риччи. Уравнение, описывающее изменение кривизны пространства во времени.
Правильный многогранник. Многогранник, граница которого состоит из одинаковых правильных многоугольников, одинаково организованных возле каждой вершины. Евклид доказал, что существует ровно пять правильных многогранников.
Правильный многоугольник. Многоугольник, у которого все стороны имеют одинаковую длину, а все углы равны (см. рис. 4).
Преобразование. Еще одно слово, обозначающее «функцию»; используется обычно в тех случаях, когда задействованные переменные представляют собой точки в некотором пространстве. К примеру, «повернуть вокруг центра на 90°» — это преобразование квадрата.
Проективная геометрия. Разновидность геометрии, в которой параллельных прямых не существует: любые две прямые пересекаются в точке. Получается из евклидовой геометрии путем добавления новой «прямой в бесконечности».
Простое число. Натуральное число, большее 1, которое невозможно получить перемножением двух меньших натуральных чисел. Первыми простыми числами являются 2, 3, 5, 7, 11, 13.
Простой идеал. Аналог простого числа для алгебраических числовых систем.
Пятиугольник. Многоугольник с пятью сторонами.
Разложение на простые множители. Процесс, при котором число записывается в виде произведения его простых делителей. К примеру, разложение числа 60 выглядит как 2² × 3 × 5.
Размерность. Число координат, необходимых для определения положения точки в данном пространстве. К примеру, размерность плоскости равна 2, а размерность пространства, в котором мы живем (по крайней мере с точки зрения геометрии Евклида) равна 3.
Ранг. Наибольшее число независимых рациональных решений уравнения, определяющего эллиптическую кривую. «Независимых» означает, что они не могут быть получены из других решений при помощи стандартного геометрического построения, которое из комбинации любых двух решений дает третье (см. рис. 25).
Рациональное число. Действительное число вида p/q, где p и q — целые числа и q ≠ 0. Пример: 22/7.
Решетка. На плоскости: множество точек, расположение которых повторяется в двух независимых направлениях, как узор на обоях (см. рис. 26). В пространстве: множество точек, расположение которых повторяется в трех независимых направлениях, как атомы в кристалле.
Решетчатая укладка. Набор одинаковых кружков или шариков, центры которых образуют решетку.
Род. Число отверстий в поверхности.
Ромбический додекаэдр. Многогранник, граница которого состоит из 12 одинаковых ромбов — параллелограммов с одинаковыми сторонами (см. рис. 15).
Ряд. Выражение, в котором складывается много — часто бесконечно много — величин.
Сводимая (сократимая) конфигурация. Часть сети, для которой характерно следующее: если сеть, полученную при ее удалении, можно раскрасить в четыре краски, то это можно сделать и с первоначальной сетью.
Симметрия. Преобразование некоторого объекта, при котором его форма в целом не меняется. К примеру, поворот квадрата на 90°.
Сингулярность. Точка, в которой происходит что-то неприятное: скажем, функция становится бесконечной или решение некоего уравнения прекращает существование.
Синус. Тригонометрическая функция угла, определяемая как sin A = b/c (см. рис. 51).
Скорость. Быстрота, с которой изменяется положение тела во времени. Скорость имеет как размер (абсолютную величину), так и направление.
Собственное число. Одно из нескольких особых чисел, связанных с оператором. Если при преобразовании некоего вектора при помощи этого оператора получается вектор, кратный первоначальному, то коэффициент кратности называется собственным числом.
Составное число. Натуральное число, которое можно получить перемножением двух меньших натуральных чисел.
Стандартная модель. Квантовомеханическая модель, описывающая все известные элементарные частицы.
Степенной ряд. То же, что многочлен, но с бесконечным количеством степеней переменной. К примеру, 1 + 2x + 3x² + 4x³ +… В определенных обстоятельствах эта бесконечная сумма приобретает вполне определенное значение, и тогда говорят, что ряд сходится.
Степень. Число, умноженное само на себя заданное количество раз. К примеру, четвертая степень 3 — это 3 × 3 × 3 × 3 = 81, обозначается 34.
Степень многочлена. Наибольшая степень переменной в многочлене. К примеру, степень многочлена 6x³ − 5x² + 4x − 7 равна 3.
Сфера. Множество всех точек в пространстве, расположенных на заданном расстоянии от некой фиксированной точки — центра. Она круглая, как мяч, но собственно сфера содержит только точки на поверхности мяча, а не внутри него.
Тангенс. Тригонометрическая функция угла, определяемая как tg A = b/a (см. рис. 51).
Топологическое пространство. Форма, которая считается «той же самой», если подвергается любому непрерывному преобразованию.
Топология. Наука о топологических пространствах.
Тор. Поверхность, похожая на бублик с одним отверстием (см. рис. 12).
Трансцендентное число. Число, не удовлетворяющее ни одному алгебраическому уравнению с рациональными коэффициентами. Примеры: π и e.
Трехмерная сфера. Трехмерный аналог сферы: множество всех точек четырехмерного пространства, лежащих на заданном расстоянии от некоей фиксированной точки — центра.
Триангуляция. Разбивка поверхности на сеть треугольников или его многомерный аналог.
Тривиальная группа. Группа, состоящая из единственного элемента, причем единичного.
Трисекция. Деление на три равных части, особенно в отношении углов.
Упаковка. Организация форм в пространстве таким образом, чтобы они не накладывались друг на друга.
Устойчивое состояние. Состояние динамической системы, в которое она возвращается, будучи подвергнута небольшому возмущению.
Фаза. Комплексное число на единичной окружности, на которое домножается квантовая волновая функция.
Фундаментальная группа. Группа, образованная гомотопическими классами петель в некоем топологическом пространстве с операцией «последовательное прохождение петель».
Функция. Правило f, которое при действии на число x дает другое число f (x). К примеру, если f (x) = log x, то f — логарифмическая функция. Переменная x может быть действительной или комплексной (в этом случае ее часто обозначают z). В более общем случае x и f (x) могут быть элементами определенных множеств (в частности, плоскости или пространства).
Хаос. Случайное, на первый взгляд, поведение детерминированной системы.
Целое число. Любое из чисел … −3, −2, −1, 0, 1, 2, 3 …
Цикл. В топологии: формальная комбинация петель в триангуляции с присвоенными им числовыми индексами. В алгебраической геометрии: формальная комбинация подмногообразий с числовыми индексами.
Частица. Масса, сосредоточенная в одной точке.
Число Ферма. Число вида, где k — натуральное число. Если это число простое, оно называется простым числом Ферма.
Шар. Заполненная сфера, т. е. сфера и то, что находится у нее внутри.
Эйлерова характеристика. F — E + V, где F — число граней в триангуляции некоего пространства, E — число ребер, а V — число узлов. Для тора с g отверстиями эта величина равна 2 − 2g при любом разбиении на треугольники.
Электромагнитное поле. Функция, задающая силу и направление электрического и магнитного полей в каждой точке пространства.
Эллиптическая кривая. Кривая на плоскости, уравнение которой имеет вид y² = ax³ + bx² + cx + d; постоянные a, b, c, d обычно считаются рациональными (см. рис. 27).
Эллиптическая функция. Комплексная функция, значение которой не меняется при прибавлении к переменной двух независимых комплексных чисел. Иными словами, f (z) = f (z + u) = f (z + v), где v не равно u, домноженному на действительный коэффициент (см. рис. 30).
notes
Назад: Гипотеза ABC
Дальше: Сноски

