2. Территория простых чисел. Проблема Гольдбаха

Некоторые великие задачи встречаются и в начальном курсе математики, хотя мы этого не замечаем. Вскоре после того, как ребенок осваивает умножение, он знакомится с концепцией простого числа. Известно, что некоторые числа могут быть получены при перемножении двух меньших чисел, к примеру: 6 = 2 × 3. Другие, такие как 5, невозможно разложить подобным образом на сомножители. Максимум, что можно сделать, это записать 5 = 1 × 5, но в этом выражении нет двух меньших чисел. Числа, которые можно разбить на сомножители, называют составными, а те, что разложить невозможно, — простыми. Простые числа кажутся такой несложной темой! Если вы уже умеете перемножать натуральные числа, то способны разобраться и в том, что представляет собой простое число. Простые числа — первичные строительные кирпичики для всех натуральных чисел, и обнаружить их можно в самых разных разделах математики. Но в них есть тайна, и, на первый взгляд, они раскиданы среди положительных целых чисел почти случайным образом. Нет никаких сомнений: простые числа — настоящая загадка. Возможно, это естественное следствие их определения — ведь определяются они не через какое-либо присущее им свойство, а напротив — через свойство, которое у них отсутствует. С другой стороны, для математики это фундаментальное понятие, поэтому мы не можем просто так в ужасе поднять руки и сдаться. Нам необходимо с ними освоиться и каким-то образом вызнать их потаенные секреты.

Некоторые свойства простых чисел очевидны. За исключением самого маленького из них, двойки, все они нечетные. Сумма цифр простого числа, за исключением тройки, не может быть кратна трем. Они, за исключением пятерки, не могут заканчиваться на цифру 5. Если же число не подпадает под эти правила — и под несколько других, более тонких, — то невозможно посмотреть на него и сразу сказать, простое это число или нет. Да, существуют формулы для простых чисел, но это в значительной степени обман. Эти формулы не дают никакой полезной новой информации о простых числах; это просто хитрый способ зашифровать определение «простоты» в виде формулы. Простые числа — как люди: каждое из них — личность, и они не подчиняются общим правилам.

За тысячелетия математики сумели постепенно расширить свои знания о простых числах. Время от времени и сегодня решаются новые серьезные проблемы, с ними связанные. Однако многие вопросы по-прежнему остаются нерешенными. Некоторые из них фундаментальны и легко формулируются, другие понятны немногим. В этой главе говорится о том, что мы знаем и чего не знаем об этих раздражающих своей неприступностью, но все же фундаментальных числах. Начинается она с установления некоторых базовых понятий: в частности, концепции разложения на простые множители — как представить заданное число в виде произведения простых чисел. Даже этот знакомый процесс заводит нас на глубину сразу же, как только мы начинаем задавать вопросы о по-настоящему эффективных методах поиска простых множителей конкретного числа. Как ни удивительно, определить, является ли данное число простым, относительно несложно, но если число составное, то отыскать его простые множители часто намного труднее.

Разобравшись в основах, перейдем к самой известной из нерешенных задач, связанных с простыми числами, — к проблеме Гольдбаха, которой уже 250 лет. В последнее время в работе над ней достигнут колоссальный прогресс, но полностью она пока не решена. А несколько других задач представят нам примеры того, что еще предстоит сделать в этой важной, но трудно поддающейся исследованию области математики.

Простые числа и разложение на множители знакомы нам из школьного курса арифметики, однако большинство интересных свойств простых чисел на этом уровне не рассматривают и никаких доказательств не представляют. Тому есть веские причины: доказательства даже самых очевидных, на первый взгляд, свойств удивительно сложны. Вместо этого школьников учат некоторым простым методикам работы с простыми числами, акцентируя внимание на вычислениях, где цифры относительно невелики. В результате наши первые впечатления от встречи с простыми числами, как правило, обманчивы.

Древние греки были знакомы с некоторыми базовыми свойствами простых чисел и знали, как их доказать. Простые числа и сомножители — основная тема Книги VII евклидовых «Начал», классического труда, посвященного геометрии. В этой книге имеется, в частности, геометрическое представление арифметических действий — деления и умножения. Греки предпочитали работать не с числами как таковыми, а с длинами линий (отрезков), но их результаты несложно переформулировать на языке чисел. Так, Предложение 16 Книги VII доказывает, что при перемножении двух чисел результат не зависит от того, в каком порядке берутся эти числа. Иными словами, ab = ba, фундаментальный закон алгебры.

В школьной арифметике простые делители используют для поиска наибольшего общего делителя двух чисел. К примеру, чтобы найти наибольший общий делитель чисел 135 и 630, мы раскладываем их на простые множители:

Затем берем все простые числа, которые присутствуют в обоих разложениях, в наибольшей общей степени; получаем 32 × 5. Перемножаем, получаем 45. Это и есть наибольший общий делитель. Из этой процедуры создается впечатление, что без разложения на простые множители невозможно найти наибольший общий делитель. На самом деле с точки зрения логики все наоборот. Предложение 2 Книги VII «Начал» представляет метод поиска наибольшего общего делителя двух натуральных чисел без разложения их на простые множители. Метод состоит в последовательном вычитании меньшего числа из большего, а затем остатка из меньшего числа и т. д. до тех пор, пока есть остаток. Для тех же чисел 135 и 630 — это достаточно типичный случай для небольших чисел — процесс выглядит так. Вычитаем 135 из 630 столько раз, сколько сможем:

630 − 135 = 495;

495 − 135 = 360;

360 − 135 = 225;

225 − 135 = 90.

Поскольку 90 < 135, переходим к той же процедуре с участием чисел 90 и 135:

135 − 90 = 45.

Поскольку 45 < 90, продолжаем то же с числами 45 и 90:

90 − 45 = 45;

45 − 45 = 0.

Таким образом, наибольший общий делитель чисел 135 и 630 равен 45.

Эта процедура работает потому, что на каждой стадии происходит замена первоначальной пары чисел более простой парой (одно из чисел уменьшается), которая тем не менее имеет тот же наибольший общий делитель. В конце концов, одно из чисел делится на второе нацело, без остатка, и процесс поиска на этом завершается. В наше время подробное описание вычислительного метода, при помощи которого можно гарантированно найти ответ той или иной задачи, называют алгоритмом. Поэтому и процедура из «Начал» Евклида известна сегодня как евклидов алгоритм. Логически эта процедура первична по отношению к процедуре разложения на простые множители. В самом деле, Евклид использует ее для доказательства основных свойств простых делителей. В современных университетских курсах математики алгоритм Евклида используется с той же целью.

Описанная процедура целиком опирается на евклидово Предложение 30 и была бы невозможна без него. В современных терминах речь в нем идет о том, что если произведение двух чисел — то, что мы получаем при их перемножении — делится на некое простое число, то на это же число должен делиться один из сомножителей. Предложение 32 заключается в том, что любое число либо само является простым, либо имеет простой делитель. Объединив оба утверждения, несложно сделать вывод, что любое число есть результат перемножения простых множителей и что их набор единственный, если не брать во внимание порядок записи. К примеру,

и т. д., но единственный реальный способ получить 60 состоит в том, чтобы взять множители из первого разложения и переставить их местами. Не существует, к примеру, разложения, в котором 60 = 7 × что-нибудь. Существование какого-нибудь разложения следует из Предложения 32. Если число простое — стоп. Если нет, находим простой делитель, делим на него, получая меньшее число, и повторяем процедуру. Уникальность набора делителей следует из Предложения 30. Так, если бы разложение 60 = 7 × что-нибудь существовало, то одно из чисел 2, 3 и 5 должно было бы тоже делиться на 7, но этого не происходит.

Здесь я должен прояснить один небольшой, но важный момент: исключительный статус числа 1. Согласно приведенному выше определению, оно простое: если мы попытаемся разбить его на множители, максимум, что мы получим, будет 1 = 1 × 1, где нет меньших чисел. Однако позже, с развитием теории, такая интерпретация вызывает проблемы, поэтому в последние век-два математики добавили в определение простого числа дополнительное ограничение. Число 1 настолько отличается от всех остальных чисел, что его следует рассматривать как исключение, — это не простое число, но и не составное. Это третья разновидность числа — единица. Одна из причин, по которым мы называем 1 особым случаем, а не относим ее к настоящим простым числам, заключается в том, что если мы согласимся с простотой единицы, то единственность набора множителей нарушится. Вообще-то 1 × 1 = 1 — уже нарушение, а уж 1 × 1 × 1 × 1 × 1 × 1 × 1 × 1 = 1 ни в какие ворота не лезет. Можно было бы изменить определение единственности и сказать «единственный, без учета дополнительных единичных множителей», но это был бы всего лишь другой способ признать, что 1 — число особое.

Много позже, в Предложении 20 Книги IX, Евклид доказывает еще один ключевой факт: «Простых чисел существует больше, чем их насчитывается в любом множестве простых чисел». Иными словами, множество простых чисел бесконечно. Это чудесная теорема и изящное доказательство, но ее появление вызвало множество проблем. Если простые числа уходят в бесконечность, но, судя по всему, расположены без всякой системы, то как можно сказать, на что они похожи?

Мы вынуждены обратиться к этому вопросу потому, что не можем оставить в стороне простые числа — очень существенную деталь математического ландшафта. Особенно часто они встречаются (и особенно полезны) в теории чисел — разделе математики, изучающем свойства целых чисел. Звучит, может быть, достаточно элементарно, но на самом деле теория чисел — один из самых глубоких и сложных разделов математики. Позже мы увидим тому множество свидетельств. В 1801 г. Гаусс, ведущий специалист того времени по теории чисел (а также, по мнению некоторых ученых, один из ведущих математиков всех времен, а может быть, и величайший из них), написал продвинутый учебник по этой теории — «Арифметические исследования» (Disquisitiones Arithmeticae). В нем среди множества сложных тем Гаусс указал, что не следует терять из виду два весьма фундаментальных вопроса: «Известно, что задача отличения простых чисел от составных и разложения последних на простые множители является одной из важнейших и полезнейших в арифметике».

В школе, как правило, учат ровно одному способу поиска простых делителей числа. Заключается он в том, чтобы пробовать по очереди все потенциальные делители, пока не найдется такой, на который число разделится нацело. Если вы не нашли ни одного делителя к тому моменту, как добрались до корня квадратного из первоначального числа — точнее, до наибольшего целого числа, меньшего или равного этому корню, — то число это простое. В противном случае вы найдете множитель, разделите на него и продолжите с новым числом с того же места. Эффективнее всего пробовать только простые делители, но для этого необходим список простых чисел. Поиск останавливается на корне квадратном из числа, потому что наименьший делитель любого составного числа не превосходит корень квадратный из этого числа. Однако для больших чисел эта процедура безнадежно неэффективна. К примеру, если взять число

то на простые множители оно раскладывается следующим образом:

и, чтобы добраться до меньшего из двух множителей, вам придется опробовать каждое из первых 624 401 249 простых чисел. Конечно, при помощи компьютера это несложно сделать, но если взять для начала число из 100 цифр, которое — так уж случилось — раскладывается на два множителя по 50 цифр в каждом, то систематический перебор последовательных простых чисел продлится до конца Вселенной и вряд ли успеет дать результат.

Нет, вообще-то современные компьютеры, как правило, умеют раскладывать числа из 100 цифр на простые множители. Моему компу требуется меньше секунды, чтобы найти простые множители числа 10⁹⁹ + 1 (выглядит это число как 1000 … 001 с 98 нулями). Это число — результат перемножения 13 простых чисел (одно из них повторяется дважды), наименьшее из которых — 7, а наибольшее — 141 122 524 877 886 182 282 233 539 317 796 144 938 305 111 168 717.

Однако если я попрошу компьютер разложить на множители число 10¹⁹⁹ + 1, в котором 200 цифр, то жужжать он будет долго, но результата так и не выдаст. Хотя, конечно, даже разложение числа из 100 цифр производит сильное впечатление. В чем тут секрет? В более эффективном по сравнению с последовательным перебором потенциальных простых делителей алгоритме поиска.

Мы сегодня знаем о первой из названных Гауссом задач (проверка числа на простоту) гораздо больше, чем знал он сам, и гораздо меньше, чем хотелось бы, о второй (разложение на простые множители). Здравый смысл говорит о том, что проверка на простоту намного проще разложения на простые множители. Как правило, это удивляет нематематиков, — ведь в школе учат проверять число на простоту тем же методом, что и искать его простые множители: перебором всех возможных делителей. Но, оказывается, существуют хитрые способы доказать простоту числа и без этого. Эти же методы позволяют доказать, что число составное, без нахождения каких бы то ни было его делителей. Достаточно показать, что это число не проходит тест на простоту.

Прапрадедушкой всех современных тестов на простоту может считаться теорема Ферма (чтобы не путать со знаменитой Великой теоремой, о которой речь пойдет в главе 7, ее иногда называют Малой теоремой Ферма). Эта теорема основана на модулярной арифметике, которую иногда называют еще «часовой арифметикой», поскольку числа в ней спирально накладываются друг на друга, как время на циферблате часов. Выберем число — для 12-часовых аналоговых часов это число 12 — и назовем его модулем. Теперь в любых арифметических вычислениях с неотрицательными целыми числами мы договоримся заменять любое число, кратное 12, нулем. К примеру, 5 × 5 = 25, но 24 — это дважды 12, поэтому вычтем из результата 24. Получим 5 × 5 = 1 по модулю 12. Модулярная арифметика очень красива, поскольку почти все обычные арифметические законы в ней тоже работают. Основная разница заключается в том, что мы не всегда можем разделить одно число на другое, даже если это не нуль. Модулярная арифметика полезна также тем, что обеспечивает удобный и аккуратный способ разбираться с вопросами делимости: какие числа делятся на те или иные модули без остатка и чему равен остаток, если это не так. Модулярную арифметику предложил Гаусс в «Арифметических исследованиях», и сегодня она широко используется не только в математике, но и в информатике, физике, инженерном деле.

Малая теорема Ферма утверждает, что если взять простой модуль p и любое число a, не кратное p, то степень (p − 1) числа a будет равна 1 по модулю p. Пусть, к примеру, p = 17 и a = 3. Тогда теорема предсказывает, что остаток от деления 3¹⁶ на 17 будет равен 1. Проверим:

Ни один человек, находящийся в своем уме, не захочет проводить подобные расчеты для, скажем, 100-значных простых чисел. К счастью, существует хитрый и быстрый способ сделать это. Смысл в том, что ответ не равен единице, если модуль, с которого мы начали, является составным числом. Так что теорема Ферма — надежная основа для эффективного теста, который обеспечивает необходимое условие простоты числа.

К несчастью, одного этого теста недостаточно. Известно, что его проходят и многие составные числа, известные как числа Кармайкла. Самое маленькое из них 561, и в 2003 г. Ред Элфорд, Эндрю Гранвиль и Карл Померанс доказали, к всеобщему изумлению, что таких чисел бесконечно много. Изумление математического сообщества вызвал тот факт, что авторам удалось найти доказательство; сам по себе результат особого удивления не вызвал. Фактически было доказано, что для каждого числа x существует по крайней мере x^2/7 чисел Кармайкла, меньших или равных x, если x достаточно велико.

Однако более сложные варианты теоремы Ферма действительно можно превратить в тесты на простоту, такие как опубликованный в 1976 г. Гэри Миллером. К несчастью, доказательство достоверности теста Миллера опирается на одну из нерешенных великих математических задач — обобщенную гипотезу Римана (глава 9). В 1980 г. Майкл Рабин превратил тест Миллера в вероятностный, т. е. такой, который может иногда давать неверный ответ. Исключения, если они существуют, встречаются очень редко, но тем не менее доказать, что их нет, невозможно.

Наиболее эффективным детерминированным (т. е. дающим гарантированный результат) тестом на сегодняшний день является тест Адлемана — Померанса — Румели, названный в честь своих создателей — Леонарда Адлемана, Карла Померанса и Роберта Румели. В нем используются концепции теории чисел, куда более сложные, чем теорема Ферма, но примерно того же характера.

Я до сих пор помню письмо одного математика-любителя, предложившего вариант испытания делением. Давайте пробовать все возможные делители, предлагал этот энтузиаст, но начинать с корня квадратного из числа и двигаться, наоборот, вниз. Иногда этот метод действительно позволяет быстрее получить результат, чем при проверке делителей в обычном порядке, но с ростом чисел он, естественно, встречается с теми же проблемами, что и обычный метод. Если применить предложенный вариант к приведенному выше примеру, 22-значному числу 1 080 913 321 843 836 712 253, то квадратный корень из него равен примерно 32 875 725 419. Вам придется перепробовать 794 582 971 простой делитель, прежде чем вы доберетесь до нужного. Это хуже, чем искать его обычным путем.

В 1956 г. знаменитый логик Курт Гедель в письме к Джону фон Нейману почти буквально повторил мольбу Гаусса. Он спрашивал, можно ли улучшить метод пробного деления, и если можно, то насколько. Фон Нейман не стал заниматься этим вопросом, но позже другие математики ответили Геделю, открыв практические методы нахождения простых чисел длиной до 100 знаков, а иногда даже больше. Эти методы, самый известный из которых называется методом квадратичного решета, появились около 1980 г. Однако почти все они либо вероятностны, либо неэффективны в следующем смысле.

Как увеличивается компьютерное время, необходимое для вычислений, с ростом объема исходных данных? При тестировании на простоту исходные данные — это не само число, а число знаков в нем. Ключевое различие в этом случае проводится между двумя группами алгоритмов — алгоритмами, принадлежащими и не принадлежащими к классу P. Если время работы алгоритма растет как некая фиксированная степень от размера исходных данных, то алгоритм принадлежит к классу P; в противном случае — не принадлежит. Грубо говоря, алгоритмы класса P полезны, тогда как те, что не принадлежат к этому классу, непрактичны. Существует, однако, промежуточная полоса своеобразной ничьей земли, где в ход идут другие соображения. Класс P получил название от понятия «полиномиальное время» — именно так замысловато математики говорят о постоянных степенях. Мы еще вернемся к теме эффективных алгоритмов позже, в главе 11.

По стандартам класса P метод пробного деления работает из рук вон плохо. На школьном уровне, где для проверки предлагаются двух— или трехзначные числа, с ним все в порядке, но при работе со 100-значными числами он абсолютно безнадежен. В общем, пробное деление никак не укладывается в P-класс. Если быть точным, то время выполнения этого алгоритма для любого n-значного числа приблизительно равняется 10^n/2, а эта величина растет быстрее, чем любая фиксированная степень n. С таким типом роста, известным как экспоненциальный, по-настоящему трудно иметь дело, это страшный сон любого, кто занимается вычислениями.

До 1980-х гг. у всех известных алгоритмов проверки на простоту, за исключением вероятностных или тех, надежность которых оставалась недоказанной, время вычислений росло экспоненциально. Однако в 1983 г. был найден алгоритм, очень соблазнительно лежащий на ничьей земле вблизи P-территории: это уже упоминавшийся тест Адлемана — Померанса — Румели. Его улучшенная версия, разработанная Генри Коэном и Хендриком Ленстрой, имела время вычисления n в степени log log n, где log — обозначение логарифма. Технически log log n может быть сколь угодно большим, поэтому данный алгоритм не относится к P-классу. Однако это не мешает ему быть пригодным к практическому использованию: если n — гуголплекс, т. е. 1 с 10¹⁰⁰ нулями, то log log n равен примерно 230. Старая шутка гласит: «Доказано, что log log n стремится к бесконечности, но никто никогда не видел, как он это делает».

Первый тест на простоту, принадлежащий к P-классу, открыли в 2002 г. Маниндра Агравал и его студенты-дипломники Нирадж Каял и Нитин Саксена. В Примечаниях можно прочитать об этом немного подробнее. Они придумали алгоритм и доказали, что время его выполнения растет пропорционально не более чем n¹²; очень скоро эта величина была уменьшена до n^7,5. Однако, несмотря на то что их алгоритм относится к P-классу и, соответственно, считается «эффективным», его преимущества не проявляются до тех пор, пока n не становится очень и очень большим. По идее этот алгоритм должен побить тест Адлемана — Померанса — Румели, когда число знаков в n приблизится к 10¹⁰⁰⁰. Но такое большое число невозможно разместить не только в память компьютера, но и вообще в известной Вселенной. Зато теперь мы точно знаем, что алгоритмы P-класса для проверки простоты числа существуют. Ясно, что поиск лучших алгоритмов в этой категории — дело стоящее. Ленстра и Померанс снизили степень с 7,5 до 6. Если еще некоторые предположения о свойствах простых чисел подтвердятся, степень можно будет снизить до 3, что приблизит нас к практическому применению подобных алгоритмов.

Но самое интересное в алгоритме Агравала — Каяла — Саксены — не результат, а метод. Он прост — по крайней мере для математиков — и отличается новизной. В основе его лежит вариант теоремы Ферма, но, вместо того чтобы работать с числами, команда Агравала использовала многочлены. Многочлен, или полином, — это комбинация степеней переменной x, такая, к примеру, как 5x³ + 4x − 1. Многочлены можно складывать, вычитать и перемножать, и обычные алгебраические законы на них тоже распространяются. В главе 3 мы поговорим о многочленах подробнее.

По-настоящему великолепная идея: расширить пространство дискурса и перенести проблему в новую область. Это тот самый случай, когда идея проста настолько, что нужно быть гением, чтобы разглядеть ее. Первый намек на нее проскользнул в статье Агравала и его научного консультанта Сомената Бисваса: авторы предложили вероятностный тест на простоту, основанный на аналоге теоремы Ферма в мире полиномов. Агравал был убежден, что вероятностный компонент этого метода может быть устранен. В 2001 г. его студенты пришли к нему с очень важным техническим замечанием. Начав в нем разбираться, команда углубилась в дебри теории чисел, но постепенно, со временем, все замечания удалось свести к единственному препятствию — вопросу существования простого числа p, такого, чтобы число p − 1 имело бы достаточно большой простой делитель. Несколько консультаций с коллегами и поиск в Интернете помогли обнаружить теорему, которую Этьен Фуври доказал в 1985 г. при помощи сложных формальных методов. Именно этого команде Агравала недоставало, чтобы доказать работоспособность алгоритма, и последняя деталь головоломки точно встала на место.

В те времена, когда теория чисел пребывала в своей башне из слоновой кости, вся эта история прошла бы незамеченной и никак не повлияла бы на жизнь остального мира. Но в последние 20 лет простые числа приобрели огромный вес в криптографии — науке о шифрах. Шифры важны не только для военных, у коммерческих компаний тоже хватает секретов. Сегодня, в век Интернета, секреты есть у каждого из нас: мы не хотим, чтобы преступники получили доступ к нашим банковским счетам и номерам кредитных карт. Мало того, все чаще в преступных целях используются и другие личные данные, так что хотелось бы уберечь их все, вплоть до клички домашней кошки. Но Интернет невероятно удобен при оплате счетов, страховании машин и заказе всего, что необходимо для поездки на отдых, и всем нам приходится мириться с риском того, что ценная частная информация попадет не в те руки.

Производители компьютеров и интернет-провайдеры пытаются снизить этот риск, предлагая пользователям различные системы шифрования. Надо сказать, что внедрение компьютеров изменило как саму криптографию, так и криптоанализ — искусство взлома шифров. В настоящее время разработано множество новых шифров. Один из самых известных шифров, который в 1978 г. придумали Рональд Ривест, Ади Шамир и Леонард Адлеман, основан на использовании простых чисел. Больших простых чисел, примерно 100-значных. Система Ривеста — Шамира — Адлемана (известная как RSA) используется во многих компьютерных операционных системах, встроена в основные протоколы безопасного интернет-соединения, ею широко пользуются правительства, корпорации и университеты. Конечно, не каждое новое открытие, имеющее отношение к простым числам, может повлиять на безопасность вашего банковского счета, но это добавляет теме интереса. Как только удается выяснить что-то новое, что помогает связать простые числа и компьютерные вычисления, это привлекает повышенное внимание. Так случилось и с тестом Агравала — Каяла — Саксены, хотя при всей своей математической элегантности и важности непосредственного практического значения он не имеет.

Тем не менее он позволил немного под другим углом рассмотреть общий вопрос криптографии по Ривесту — Шамиру — Адлеману, и результат вызывает некоторые опасения. До сих пор не существует ни одного алгоритма P-класса для решения второй из названных Гауссом задач — разложения на простые множители. Большинство специалистов сходятся во мнении, что такого алгоритма не существует, но в последнее время их уверенность несколько поколебалась. Поскольку где-то за кулисами, совсем рядом, могут скрываться и другие открытия, подобные тесту Агравала — Каяла — Саксены и основанные на таких же простых идеях, как полиномиальная версия теоремы Ферма (и не важно, что пока о них никто даже не подозревает), может оказаться, что системы шифрования, основанные на разложении числа на простые множители, не настолько надежны, как нам хочется верить. Так что пока не стоит раскрывать в Интернете кличку вашей кошки!

Даже элементарная математика простых чисел ведет к выдвижению более сложных концепций. Евклид доказал, что простые числа уходят в бесконечность, так что невозможно просто перечислить их все и успокоиться. Мы не можем также дать простую и практичную алгебраическую формулу для вычисления всех простых чисел подряд, примерно так, как по формуле x² вычисляются квадраты чисел. (Простые формулы существуют, но они «мошенничают», встраивая в формулу сами простые числа под разными личинами, и в результате не сообщают нам ничего нового.) Пытаясь познать природу этих неуловимых и странных чисел, мы экспериментируем, ищем в них признаки структурированности и пытаемся доказать, что найденные нами закономерности присутствуют во всех простых числах, какими бы большими они ни были. Можно, к примеру, задаться вопросом о том, как простые числа распределены среди всех целых чисел. Таблицы простых чисел позволяют предположить, что чем дальше, тем таких чисел становится меньше. В табл. 1 показано, сколько простых чисел содержится в разных диапазонах на 1000 последовательных целых чисел.

Таблица 1. Количество простых чисел в последовательных интервалах по 1000 чисел

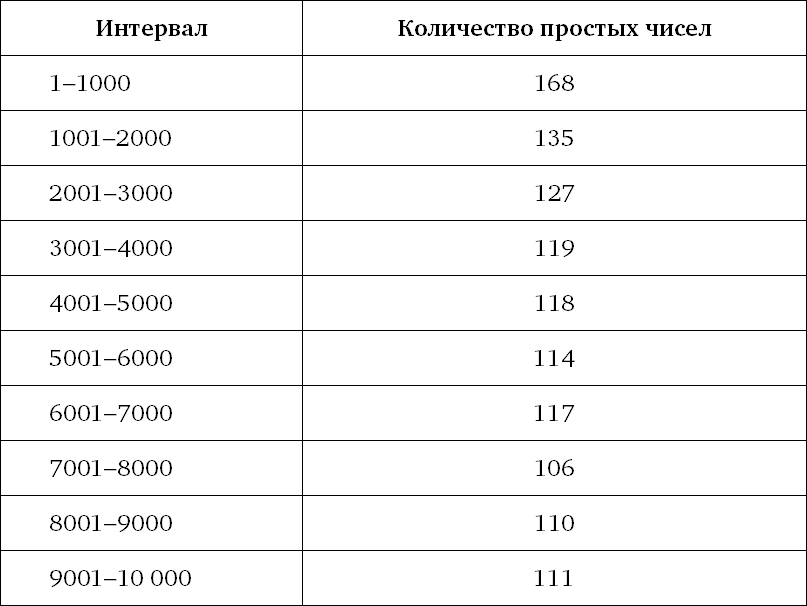
Числа во второй колонке по большей части уменьшаются сверху вниз, хотя иногда ненадолго изменяют свое поведение: к примеру, после 114 мы видим 117. Это симптом нерегулярности простых чисел, но в целом общая тенденция прослеживается достаточно четко: чем больше числа, тем реже среди них встречаются простые. За объяснением не нужно далеко ходить: чем больше становится число, тем больше у него потенциальных делителей. А простые числа должны избегать каких бы то ни было делителей. Это напоминает ловлю составных (непростых) чисел рыболовной сетью: чем гуще становится сеть, тем меньшему числу простых чисел удается сквозь нее проскользнуть.

У этой «сети» есть даже название: решето Эратосфена. Эратосфен Киренский — древнегреческий математик, живший около 276–194 гг. до н. э. Он также был атлетом, интересовался поэзией, географией, астрономией и музыкой. Эратосфен первым сумел разумным образом оценить размеры Земли, обратив внимание на положение солнца в полдень в двух разных местах — Александрии и Сиене (современный Асуан). В Сиене солнце в полдень стояло точно над головой, а в Александрии отстояло от вертикали примерно на 7°. Поскольку угол в 7° составляет одну пятидесятую часть круга, то и окружность Земли должна в 50 раз превосходить расстояние от Александрии до Сиены. Эратосфен не мог непосредственно измерить это расстояние, поэтому он спросил у караванщиков, сколько времени занимает путешествие на верблюдах из одного города в другой, и оценил, сколько в среднем проходят верблюды за день. Результат своих расчетов он привел в тогдашних единицах расстояния — стадиях, но мы не знаем, чему равнялась стадия. Историки сходятся во мнении, что оценка Эратосфена оказалась достаточно точной.

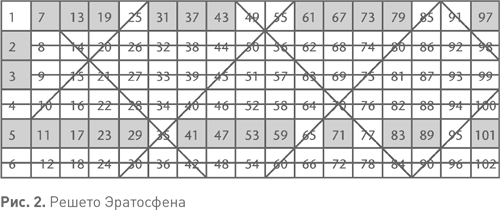
Решето Эратосфена представляет собой алгоритм поиска всех простых чисел путем последовательного исключения из числового ряда чисел, кратных уже известным простым. Рисунок 2 иллюстрирует этот метод на числах от 1 до 102, организованных так, чтобы процесс исключения кратных чисел был хорошо виден. Чтобы посмотреть, как все происходит, я советую вам составить эту или подобную ей схему самостоятельно, с нуля. Для начала начертите табличку и заполните ее числами, ничего не закрашивая и не перечеркивая. Затем потихоньку начинайте вычеркивать. Исключите 1, потому что это единица. Следующее число — 2, значит, оно простое. Вычеркните все числа, кратные 2: это те, что лежат на горизонталях, начинающихся с чисел 4, 6 и 8. Следующее невычеркнутое число — 3, следовательно, оно простое. Вычеркните все числа, кратные 3: это горизонтальный ряд, начинающийся с 6 (уже вычеркнут) и с 9. Следующее невычеркнутое число — 5, оно простое. Вычеркиваем все числа, кратные 5: они находятся на диагональных линиях, идущих слева снизу вверх направо и начинающихся на 10, 30, 60 и 90. Следующее невычеркнутое число — 7, оно простое. Вычеркиваем все числа, кратные 7: это диагонали, проходящие сверху слева вниз направо и начинающиеся на 14, 49 и 91. Затем 11 — оно не вычеркнуто, и это простое число. Первое число, кратное 11 и до сих пор не вычеркнутое (т. е. не имеющее меньших делителей) — 121, — находится за пределами нашей таблички. Процесс окончен. Оставшиеся числа в серых ячейках и есть искомые простые числа.

Решето Эратосфена — не просто историческая диковинка, это и сегодня один из наиболее эффективных методов составления длинных списков простых чисел. А родственные ему методы позволили достичь значительного прогресса в решении самой знаменитой, наверное, из великих нерешенных проблем, имеющих отношение к простым числам: проблемы Гольдбаха. Немецкий математик-любитель Кристиан Гольдбах переписывался со многими знаменитостями своего времени. В 1742 г. в письме к Леонарду Эйлеру он изложил несколько любопытных гипотез, связанных с простыми числами. Позже историки заметили, что Рене Декарт ранее писал примерно то же самое. Первое из утверждений Гольдбаха звучало так: «Всякое целое число, которое можно представить как сумму двух простых, можно записать также как сумму произвольного числа простых, пока все слагаемые не станут единицами». Второе утверждение, добавленное уже на полях письма, гласило: «Всякое целое число больше двух можно представить как сумму трех простых». Сегодняшнее определение простого числа предполагает очевидные исключения из обоих утверждений. Так, 4 не есть сумма трех простых, поскольку наименьшее простое число — 2, и сумма трех простых не может быть меньше 6. Однако во времена Гольдбаха число 1 считалось простым. Разумеется, его утверждения можно переформулировать в соответствии с современными представлениями.

В ответном письме Эйлер припомнил предыдущий разговор с Гольдбахом, когда тот указал, что первое его заявление является следствием более простой, третьей гипотезы: «Всякое четное целое есть сумма двух простых». С учетом общепринятого представления о 1 как о простом числе из этого утверждения прямо следует вторая гипотеза, поскольку любое число можно выразить как n + 1 или n + 2, где n — четное. Если n есть сумма двух простых, то исходное число есть сумма трех простых. Мнение Эйлера о третьем заявлении было однозначным: «Я считаю, что это, несомненно, верная теорема, хотя и не могу ее доказать». Собственно, на сегодняшний день статус этой гипотезы практически не изменился.

Современный подход, при котором 1 — не целое число, разбивает гипотезу Гольдбаха на две части. Вариант для четных чисел (так называемая бинарная проблема Гольдбаха) гласит: любое четное целое число больше двух можно представить в виде суммы двух простых чисел.

А вот вариант для нечетных (известный как тернарная проблема Гольдбаха): любое нечетное число больше 5 можно представить в виде суммы трех простых чисел.

Из бинарной гипотезы автоматически следует тернарная, но не наоборот. Есть смысл рассматривать эти гипотезы по отдельности, поскольку мы до сих пор не знаем точно, верна ли хоть одна из них. Но, похоже, тернарная проблема немного проще, в том смысле что продвинуться в этом направлении удалось заметно дальше.

Бинарную гипотезу Гольдбаха для малых чисел можно подтвердить несложными вычислениями:

Несложно продолжить ряд примеров вручную, скажем, до 1000 или около того, а можно и дальше, если хватит терпения. К примеру, 1000 = 3 + 997, а 1 000 000 = 17 + 999 983. В 1938 г. Нильс Пиппинг проверил бинарную гипотезу Гольдбаха для всех четных чисел вплоть до 100 000.

При этом выявилась общая тенденция: чем больше само число, тем больше способов представить его в виде суммы простых. Это отвечает здравому смыслу. Если вы возьмете большое четное число и начнете вычитать из него по очереди простые числа, с какой вероятностью все результаты этих действий окажутся составными? Достаточно в списке разностей появиться хотя бы одному простому числу, — и можно считать, что гипотеза для исходного числа подтверждена. Обратившись к статистическим свойствам простых чисел, можно оценить вероятность такого исхода. В 1923 г. аналитики Харольд Харди и Джон Литлвуд проделали такую операцию и вывели правдоподобную, но нестрогую формулу для числа способов представления заданного четного n в виде суммы двух простых чисел: это число приблизительно равно n/[2 (log n)²]. Это число увеличивается с ростом n и, кроме того, хорошо согласуется с числовыми данными. Но даже если математикам удалось бы сделать эту формулу точной, невозможно было бы исключить возможность того, что из нее существуют очень редкие, но все же исключения, так что формула не слишком помогает.

Основное препятствие, мешающее доказать гипотезу Гольдбаха, заключается в том, что она сочетает в себе две очень разные характеристики. Простые числа определяются через умножение, а в самой гипотезе речь идет о сложении. Поэтому необычайно трудно соотнести желаемый вывод с каким бы то ни было разумным свойством простых чисел. Такое впечатление, что рычаг просто некуда вставить. Должно быть, эти слова звучали настоящей музыкой в ушах владельцев издательства Faber & Faber, когда в 2000 г. они пообещали премию в 1 000 000 долларов за доказательство гипотезы. Сделано это было ради продвижения романа Апостолоса Доксиадиса «Дядя Петрос и проблема Гольдбаха». Сроки поджимали: решение необходимо было представить до апреля 2002 г. Премия эта так никому и не досталась, что едва ли удивительно, если учесть, что проблема Гольдбаха остается нерешенной уже более 250 лет.

Гипотезу Гольдбаха часто формулируют иначе — как вопрос о сложении множеств целых чисел. Бинарная проблема Гольдбаха — простейший пример такого подхода, поскольку при этом мы складываем всего лишь два множества. Для этого нужно взять любое число из первого множества, добавить к нему любое число из второго и составить из всех таких сумм свое, третье множество. Так, сумма множеств {1, 2, 3} и {4, 5} содержит 1 + 4, 2 + 4, 3 + 4, 1 + 5, 2 + 5, 3 + 5, т. е. {5, 6, 7, 8}. Некоторые числа возникают здесь не по одному разу; к примеру, 6 = 2 + 4 = 1 + 5. Я называю подобные повторы перекрытием.

Теперь можно сформулировать бинарную гипотезу Гольдбаха заново: если сложить множество простых чисел с самим собой, то полученное в результате множество будет содержать все четные числа больше двух. Такое изменение формулировки может показаться немного банальным — так оно, кстати, и есть, — но оно помогает переместить проблему в ту область математики, где есть некоторые убедительные теоремы общего характера. Немного мешает число 2, но от него можно без труда избавиться. 2 — единственное целое простое число, и при сложении его с любым другим простым числом результат получается нечетный. Так что во всем, что касается гипотезы Гольдбаха, о двойке можно просто забыть. Однако 2 + 2 нам потребуется для представления числа 4, поэтому нам придется ограничить свое внимание четными числами начиная с 6.

В качестве эксперимента рассмотрим простые числа до 30 включительно. Таких чисел девять: {3, 5, 7, 11, 13, 17, 19, 23, 29}. При сложении этого множества с самим собой получится то, что можно увидеть на рис. 3: я выделил суммы, меньшие или равные 30 (диапазон четных чисел, в который укладываются все простые до 29) жирным шрифтом. При таком представлении результата ясно видны две простые закономерности. Во-первых, вся таблица симметрична относительно главной диагонали, поскольку a + b = b + a. И, во-вторых, выделенные числа занимают приблизительно левую верхнюю половину таблицы (см. рис. 3) над жирной (проходящей по диагонали) линией. Мало того, в середине они даже норовят вылезти за нее. Происходит это потому, что в среднем большие простые числа встречаются реже, чем маленькие. Дополнительная выпуклость посередине с лихвой компенсирует числа 32 в верхнем правом и нижнем левом углах.

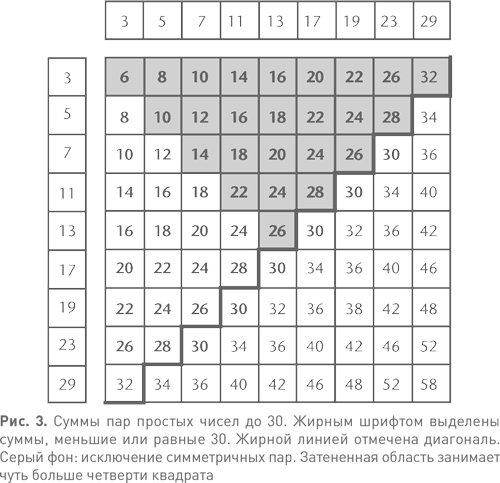
Теперь мы можем сделать некоторые грубые оценки. Я мог бы быть более точным, но этого вполне достаточно. Число ячеек в таблице составляет 9 × 9 = 81. Около половины чисел в этих ячейках находятся в левом верхнем треугольнике. Благодаря симметрии все числа, кроме лежащих на диагонали, имеют симметричную пару, так что число независимых ячеек составляет примерно 81/4, т. е., округляя, 20. В интервале от 6 до 30 содержится 13 четных чисел, поэтому 20 (и даже больше) выделенных чисел могут принимать лишь 13 четных значений. Это значит, что в данном диапазоне потенциальных сумм двух простых больше, чем четных чисел. Представьте, что вы на ярмарке и вам нужно 20 мячиками поразить 13 мишеней. Согласитесь, что шанс попасть в большую часть из них у вас будет неплохой. Тем не менее по нескольким вы можете и промазать. Иными словами, не исключено, что некоторых четных чисел все же будет не хватать.

В данном случае все числа на месте, но практические аргументы такого рода не позволяют полностью исключить подобную возможность. Однако из этого примера видно, что перекрытий должно быть немало: ведь одни и те же выделенные числа встречаются в интересующей нас четверти таблицы по несколько раз. Почему? Потому что 20 сумм должны уложиться в множество, где всего 13 членов. Поэтому каждое выделенное число в среднем встречается в таблице 1,5 раза. (Реальное количество сумм — 27, и более точная оценка показывает, что каждое выделенное число встречается дважды.) Если же каких-то четных чисел в таблице не хватает, то перекрытие должно быть еще больше.

Можно сыграть в ту же игру в более широком диапазоне, с более высоким верхним пределом — скажем, до одного миллиона. Формула, известная как теорема о распределении простых чисел (см. главу 9), дает нам возможность подсчитать количество простых чисел в интервале до любого заданного числа x. Эта оценка — x/log x. В интервале до 1 000 000 количество простых оценивается по этой формуле в 72 380. (Точное их число 78 497.) Серый фон занимает около четверти соответствующей таблицы, поэтому в нем примерно n²/4 = 250 млрд выделенных чисел — столько в этом диапазоне возможных сумм двух простых. Это намного больше, чем количество четных чисел в этом же диапазоне (их полмиллиона). Теперь перекрытие должно быть гигантским, а суммы должны возникать в среднем по 500 000 раз каждая. Так что шанс на то, что какое-то четное число окажется пропущено, многократно снижается.

Приложив еще некоторые усилия, мы можем с помощью этого метода оценить вероятность того, что некое четное число в заданном диапазоне не окажется суммой двух простых, исходя из того, что простые числа распределяются случайно с периодичностью, описываемой теоремой о распределении простых чисел, т. е. что в диапазоне до любого заданного x находится около x/log x простых чисел. Именно это сделали Харди и Литлвуд. Они понимали, что такой подход не является строгим, поскольку простые числа определяются достаточно специфически и распределены на самом деле не случайно. Тем не менее разумно ожидать, что реальные результаты не войдут в противоречие с этой вероятностной моделью, поскольку определяющее свойство простых чисел, судя по всему, очень слабо связано с тем, что происходит при сложении двух таких чисел.

Несколько стандартных методов в этой области математики используют примерно такой же подход, но стараются дополнительными средствами сделать свою аргументацию как можно более строгой. В качестве примера можно привести различные варианты решета, построенные на базе решета Эратосфена. Общие теоремы о плотности чисел в сумме двух множеств и возникающие в ней при очень больших множествах пропорции также оказываются весьма полезными инструментами.

В случаях, когда математическая гипотеза в конце концов находит подтверждение, ее история часто развивается по стандартному шаблону. На протяжении некоторого времени разные люди доказывают верность этой гипотезы при каких-либо ограничениях. Каждый такой результат улучшает предыдущий и снимает часть ограничений, но со временем этот путь исчерпывает свои возможности. Наконец появляется новая остроумная идея — и завершает доказательство.

К примеру, гипотеза в теории чисел может утверждать, что каждое положительное целое число может быть представлено каким-то определенным образом с использованием, скажем, шести специфических чисел (простых, квадратов, кубов, каких угодно еще). Здесь ключевыми моментами являются каждое положительное целое и шесть специфических чисел. Первые попытки подступиться к этой проблеме дают слабые результаты, но постепенно, посредством небольших шажков, они улучшаются.

Первым шагом часто является доказательство какого-нибудь утверждения вроде, например, такого: каждое положительное целое число, которое не делится на 3 и 11, за исключением некоторого конечного их количества, может быть представлено через некое гигантское количество — скажем, 10⁶⁶⁶ — чисел оговоренного вида. Как правило, такая теорема умалчивает о том, сколько и каких существует исключений, так что результат невозможно приложить непосредственно к любому заданному целому числу. Следующий шаг состоит в том, чтобы обозначить границы эффективности, т. е. доказать, что каждое целое число больше 10¹⁰⁴² может быть представлено таким образом. Затем снимается ограничение по делимости на 3, а немного позже и на 11. После этого авторы один за другим начинают снимать ограничения: одни уменьшают число 10⁶⁶⁶, другие 10¹⁰⁴², третьи — то и другое одновременно. Типичным улучшением может быть, к примеру, такое: каждое целое число больше 5,8 × 10¹⁷ может быть представлено с использованием не более 4298 чисел оговоренного вида.

Тем временем другие исследователи продвигаются снизу вверх, начиная с маленьких чисел, и доказывают, часто при помощи компьютерных расчетов, что, скажем, каждое число, меньшее или равное 10¹², может быть выражено с использованием не более шести тех самых чисел. Примерно за год 10¹² превращается (за пять последовательных шагов, усилиями разных исследователей или групп) в 11,0337 × 10²⁹. Следует отметить, что ни один из перечисленных шагов не является ни рутинным, ни простым; напротив, они совершаются с привлечением хитроумных специальных методов, которые ничего не говорят о более общем подходе, и доказательство при каждом последовательном шаге становится все более сложным и длинным. Через несколько лет такого постепенного продвижения это число при помощи примерно тех же идей, но более мощных компьютеров и новых ухищрений удается поднять до 10⁴³. На этом, однако, метод стопорится, и все сходятся во мнении, что никакие уловки не помогут таким способом доказать полный вариант.

Гипотеза пропадает из виду, над ней уже никто не работает. Бывает, что продвижение почти совсем останавливается. Иногда без новостей проходит лет 20… И вдруг, как гром среди ясного неба, какие-нибудь Чизбургер и Чипс заявляют, что им удалось получить полное доказательство, переформулировав гипотезу в терминах комплексных метаэргодических квазимножеств и приложив теорию византийского квислинга. После нескольких лет споров о тонких моментах логики и затыкания нескольких дыр в доказательстве математическое сообщество признает его корректным и немедленно задается вопросами, не существует ли более простого способа получить тот же результат и нельзя ли его улучшить.

В последующих главах вы не раз увидите эту схему в действии. Но если рассказывать обо всем этом подробно, то может получиться довольно скучно, поэтому я не буду перечислять всех, кому удалось более точно определить экспоненту в гипотезе Джекила — Хайда, выяснив, что это не 1,773, а 1,771 + e для любого положительного e (как бы ни гордились Баггинс и Крумм своим последним достижением на этой ниве). Я опишу несколько значимых вкладов, оставив все другие за скобками. И дело не в том, что работа Баггинса и Крумма кажется мне незначительной. Может быть, она даже вымостила дорогу к прорывному открытию Чизбургера — Чипса. Но, по правде говоря, только специалисты, внимательно следящие за развитием событий, могут затаив дыхание ждать следующего крошечного шажка.

Поэтому в будущем я буду опускать некоторые подробности, но сейчас давайте посмотрим, как развивался процесс в случае с проблемой Гольдбаха.

Уже доказаны некоторые теоремы, помогающие продвинуться по пути решения проблемы Гольдбаха. Первый серьезный прорыв произошел в 1923 г., когда Харди и Литлвуд при помощи своих аналитических методов доказали тернарную гипотезу Гольдбаха для всех достаточно больших нечетных чисел. Однако их доказательство опиралось на другую великую проблему — обобщенную гипотезу Римана, о которой мы поговорим в главе 9. Эта проблема до сих пор остается нерешенной, так что в доказательстве Харди и Литлвуда есть существенный пробел. В 1930 г. Лев Шнирельман сумел заполнить этот пробел при помощи замысловатого варианта их собственных рассуждений, основанных на методах решета. Он доказал, что ненулевая доля всех чисел может быть представлена в виде суммы двух простых. Добавив к этому результату некоторые общие рассуждения о сложении последовательностей, он доказал, что существует такое целое число С, что любое натуральное число есть сумма не более С простых чисел. Это число получило известность как постоянная Шнирельмана. В 1937 г. аналогичные результаты получил Иван Виноградов, но его метод также не позволял сказать конкретно, насколько велики «достаточно большие» числа. В 1939 г. Константин Бороздин доказал, что они начинаются не позже чем с числа 3^14 348 907. К 2002 г. Лю Минчит и Ван Тяньцзэ снизили границу «достаточно больших чисел» до e³¹⁰⁰, что равняется примерно 2 × 10¹³⁴⁶. Это число гораздо меньше, но все же слишком велико для того, чтобы все нижележащие числа можно было проверить перебором на компьютере.

В 1969 г. Николай Климов сумел установить, что постоянная Шнирельмана не превышает 6 млрд. Другим математикам удалось сделать более точную оценку, и в 1982 г. Ханс Ризель и Роберт Воган снизили эту цифру до 19. Хотя 19, разумеется, многим лучше 6 млрд, все признаки указывают на то, что на самом деле постоянная Шнирельмана равняется всего лишь 3. В 1995 г. Лешек Каницкий снизил верхний предел до 6 в общем случае и до 5 для нечетных чисел, но ему тоже пришлось предположить истинность гипотезы Римана. Его результаты вместе с численной проверкой гипотезы Римана вплоть до 4 × 10¹⁴, которую осуществил Йорг Рихштейн, доказали бы, что постоянная Шнирельмана не превосходит 4, но опять же при условии истинности гипотезы Римана. В 1997 г. Жан-Марк Дезуйе, Гоув Эффингер, Херман те Риле и Дмитрий Зиновьев показали, что из обобщенной гипотезы Римана (см. главу 9) следует тернарная гипотеза Гольдбаха. Иными словами, каждое нечетное число, за исключением 1, 3 и 5, является суммой трех простых чисел.

Поскольку на данный момент гипотеза Римана не доказана, имеет смысл постараться снять это условие. В 1995 г. французский математик Оливье Рамаре снизил верхнюю оценку для представления нечетных чисел до 7 без использования гипотезы Римана. Более того, он доказал более сильное утверждение: каждое четное число является суммой не более чем шести простых чисел. (Чтобы разобраться с нечетными числами, вычтем из любого нечетного 3: результат четный, поэтому он является суммой шести или менее простых. Первоначально взятое нечетное есть эта сумма плюс простое число 3, т. е. для его получения требуется не более семи простых.) Главным прорывом стало уточнение существующих оценок для некоторой части чисел определенного диапазона до двух: эти числа являются суммой двух простых. Ключевой результат Рамаре состоит в том, что для любого числа n больше e⁶⁷ (это примерно 1,25 × 10²⁹) по крайней мере пятая часть чисел, лежащих между n и 2n, является суммой двух простых. Далее при помощи методов решета и теоремы Ганса-Генриха Остманна о суммах последовательностей, доработанной Дезуйе, можно доказать, что каждое четное число, большее 10³⁰, есть сумма максимум шести простых чисел.

Остается разобраться лишь с промежутком между 4 × 10¹⁴, до которого Йорг Рихштейн проверил теорему численно при помощи компьютера, и 10³⁰. Как часто бывает, эти числа слишком велики для непосредственной компьютерной проверки, поэтому Рамаре доказал целую серию специализированных теорем о количестве простых чисел в небольших интервалах. Эти теоремы опираются на истинность гипотезы Римана в определенных пределах, что можно проверить при помощи компьютера. Так что доказательство состоит преимущественно из концептуальных теоретических рассуждений с привлечением компьютера для решения этой узкой задачи. Рамаре закончил свою статью указанием на то, что при помощи аналогичного подхода в принципе можно было бы снизить число простых с 7 до 5. Однако на этом пути возникают очень серьезные практические препятствия, и он написал, что такое доказательство «невозможно провести при помощи современных компьютеров».

В 2012 г. Теренс Тао преодолел эти препятствия, используя в корне другой подход. Он разместил в Интернете статью, которая в настоящий момент (когда я пишу все это) рассматривается для публикации. Основу работы составляет следующая теорема: каждое нечетное число можно представить в виде суммы не более чем 5 простых чисел. Это снижает постоянную Шнирельмана до 6. Тао получил известность благодаря своей способности решать сложные проблемы в самых разных областях математики. Его доказательство использует для решения проблемы несколько мощных методик и требует привлечения компьютеров. Если число 5 в теореме Тао удалось бы снизить до 3, то тернарная гипотеза Гольдбаха была бы доказана, а верхняя граница для постоянной Шнирельмана снижена до 4. Тао подозревает, что сделать это возможно, но нужны новые идеи.

Бинарная гипотеза Гольдбаха представляется еще сложнее. В 1998 г. Дезуйе, Саутер и те Риле проверили ее для всех четных чисел вплоть до 10¹⁴. К 2007 г. Томаш Оливейра-и-Сильва улучшил этот результат до 10¹⁸ и продолжает расчеты. Мы знаем, что каждое четное целое число можно представить в виде суммы не более чем шести простых чисел — это доказал Рамаре в 1995 г. В 1973 г. Чэнь Цзинжунь доказал, что каждое достаточно большое четное целое может быть представлено в виде суммы простого и полупростого (это либо простое число, либо произведение двух простых) чисел. Близко, но не то. Тао заявил, что бинарную гипотезу Гольдбаха невозможно доказать при помощи его методов. Сложение трех простых чисел дает гораздо большее перекрытие результатов в том смысле, в каком мы говорили о перекрытии при обсуждении рис. 3, чем сложение двух простых, фигурирующих в бинарной гипотезе Гольдбаха, а методы и Тао, и Рамаре неоднократно используют это свойство.

Итак, через несколько лет мы, возможно, получим полное доказательство тернарной гипотезы Гольдбаха, из которой, в частности, следует, что каждое четное число можно представить в виде суммы не более чем четырех простых. Но бинарная гипотеза Гольдбаха, вероятно, будет по-прежнему ставить математиков в тупик.

За 2300 лет, прошедших с момента, когда Евклид доказал несколько базовых теорем о простых числах, мы узнали о них немало. Однако остается еще очень много того, чего мы по-прежнему не знаем.

К примеру, мы знаем, что существует бесконечно много простых чисел вида 4k + 1 и 4k + 3. В более общем виде это утверждение выглядит так: любая арифметическая прогрессия ak + b с постоянными параметрами a и b содержит бесконечно много простых чисел, если a и b не имеют общих делителей. К примеру, пусть a = 18. Тогда b = 1, 5, 7, 11, 13 или 17. Следовательно, существует бесконечно много простых чисел видов 18k + 1, 18k + 5, 18k + 7, 18k + 11, 18k + 13 или 18k + 17. Но это неверно для 18k + 6, например, потому что 18 кратно 6. Ни одна арифметическая прогрессия не может состоять только из простых чисел, но недавний серьезный прорыв — теорема Грина — Тао — показывает, что последовательность простых чисел содержит арифметические прогрессии произвольной длины. В 2004 г. Бен Грин и Теренс Тао разработали очень глубокое и сложное доказательство этого утверждения, что внушает надежду: на самые сложные вопросы, какими бы неприступными они ни выглядели, в конце концов может быть получен ответ.

Снимаем шляпу, а потом надеваем ее — и вновь за работу: мы немедленно задаемся вопросом о более сложных формулах с k. Не существует простых чисел вида k²; не существует и простых вида k²−1, за исключением 3, поскольку подобные выражения раскладываются на множители. Однако выражение k² + 1 не имеет очевидных делителей, и простых чисел такого вида можно найти множество:

Можно привести пример и с бо́льшими цифрами, хотя особого смысла в этом нет:

Предполагается, что таких простых чисел тоже бесконечно много, но до сих пор не доказано ни одного подобного утверждения ни для одного конкретного многочлена, в котором k стояло бы в степени выше единицы. Очень правдоподобное предположение сделал в 1857 г. Виктор Буняковский: любой многочлен от k, не имеющий очевидных делителей, представляет бесконечное множество простых чисел. Исключение составляют не только разложимые многочлены, но и такие многочлены, как k² + k + 2 (этот многочлен всегда делится на 2, хотя и не имеет алгебраических делителей).

Некоторые многочлены, судя по всему, обладают особыми свойствами. Классический пример: k² + k + 41. Этот простое число, если k = 0, 1, 2, …, 40 и, строго говоря, если k = −1, −2, …, — 40 тоже. Длинные цепочки простых чисел при последовательных значениях k попадаются редко, и о них мы кое-что знаем. Но в целом вся эта область весьма загадочна.

Гипотеза о парах простых чисел почти так же знаменита, как гипотеза Гольдбаха, и, судя по всему, столь же неприступна. Вот ее суть: существует бесконечно много пар простых чисел с разницей в 2. Приведем несколько примеров:

На сегодняшний день (на январь 2012 г.) наибольшими известными парными простыми являются числа 3 756 801 695 685 × ^2666 669 ± 1, содержащие по 200 700 десятичных знаков. Они были найдены в 2011 г. в рамках проекта распределенных вычислений PrimeGrid. В 1915 г. Вигго Брун при помощи одного из вариантов решета Эратосфена доказал, что сумма чисел, обратных всем парным простым, сходится, в отличие от суммы чисел, обратных всем простым. В этом смысле парные простые встречаются относительно редко. При помощи аналогичных методов он доказал также, что существует бесконечно много целых n, таких, что n и n + 2 имеют не больше девяти простых делителей. Харди и Литлвуд при помощи своих эвристических методов пришли к выводу, что количество пар простых, меньших x, асимптотически приближается к

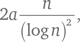
где a — константа, равная приблизительно 0,660161. Идея в том, что в данном случае можно считать простые числа возникающими случайно с частотой, которая делает общее число простых вплоть до x приблизительно равным x/log x. Аналогичных гипотез и эвристических формул существует множество, но строгих доказательств для них опять же не существует.

Да, в математике есть сотни открытых вопросов, имеющих отношение к простым числам. Одни из них просто любопытны, другие глубоки и имеют большую важность. С некоторыми вопросами из последней категории нам еще предстоит встретиться в главе 9. Ведь несмотря на все успехи математики за последние 2500 лет, скромные простые числа не потеряли ни своей притягательности, ни загадочности.