Не существует готовой «замкнутой» формулы для суммы гармонического ряда

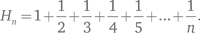
Более того, такой формулы, по всей вероятности, не существует. Однако существует прекрасная ее аппроксимация: по мере того как n увеличивается, Hn стремится к logn + γ. Здесь γ — постоянная Эйлера, численно равная примерно 0,5772156649. Эйлер вывел эту формулу в 1734 г., а Лоренцо Маскерони изучал постоянную в 1790 г. Ни тот, ни другой не использовали символ γ.

Постоянная Эйлера — одно из тех странных чисел, которые время от времени возникают в математике (вспомните π и e); у них нет красивого или простого выражения, они то и дело появляются в самых разных местах, но при этом складывается впечатление, что они существуют сами по себе. В главе 3 мы убедились, что и π, и e трансцендентны: они не являются решениями каких-либо алгебраических уравнений с целыми коэффициентами. Они иррациональны: не выражаются точными дробями. Многие математики считают, что постоянная Эйлера трансцендентна, но мы даже не знаем наверняка, иррациональна ли она. Если все же γ = p/q для целых p и q, то q равняется по крайней мере 10^242 080.

Постоянная Эйлера важна во многих областях математики — от римановой дзета-функции до квантовой теории поля. Она появляется во многих ситуациях и в многочисленных формулах. Поэтому просто возмутительно, что мы не можем решить, рациональна ли она!