Книга: Тайны чисел: Математическая одиссея
Назад: Должен ли вратарь мадридского «Реала» играть в футболке с номером 1?
Дальше: Отчего простые числа 17 и 29 являются ключом к концу времени?
Почему американскому виду цикады нравится простое число 17?
В лесах Северной Америки живет вид цикады с очень необычным жизненным циклом. На протяжении 17 лет эти цикады прячутся под землей и почти ничем не проявляют себя, разве что присасываются к корням деревьев. Но затем, в мае 17-го года, они появляются на поверхности в огромных количествах и вторгаются в лес: их число на каждом акре (0,4 гектара) доходит до миллиона.
Цикады громко распевают, пытаясь привлечь пару. Все вместе они поднимают такой шум, что местные жители зачастую уезжают во время этого вторжения, повторяющегося раз в 17 лет. Боб Дилан услышал эту какофонию цикад, оккупировавших леса вокруг Принстона, когда получал почетную степень университета в 1970 г. Это вдохновило его на написание песни «День цикад» (Day of the Locusts).
Привлекшие самцов самки после оплодотворения откладывают около 600 яиц на поверхности. По прошествии 6 недель буйства все цикады умирают, и лес снова затихает на 17 лет. Вылупление следующего поколения цикад происходит в середине лета, личинки падают на лесную почву и погружаются в нее, пока не находят подходящий корень для питания. Затем они ждут следующие 17 лет до наступления очередного великого вторжения цикад.
То, что цикады могут отсчитать прошествие 17 лет, – совершенно замечательное достижение биологической инженерии. Случаи, когда какая-либо цикада появляется годом раньше или годом позже, крайне редки. Ежегодный цикл, которого придерживаются большинство животных и растений, обусловлен вариациями температуры и сменой времен года. И по-видимому, ничто в природе не учитывает то обстоятельство, что Земля совершила 17 оборотов вокруг Солнца, чтобы побудить этих цикад к появлению.
Для математика самая любопытная особенность состоит в выборе числа: ведь 17 – простое число. Является ли всего-навсего совпадением то, что цикады проводят под землей простое число лет? По-видимому, нет. Есть вид цикад, который скрывается под землей 13 лет, а также другой вид, с 7-летним циклом. Все это простые числа. Довольно удивительно, что если цикада с 17-летним циклом появляется слишком рано, то сдвиг уже будет не на год, а обычно на 4 года, тем самым происходит переключение на 13-летний цикл. Кажется, в простых числах есть что-то, способствующее всем этим разновидностям цикад. Но что же это?
Хотя ученые и не пришли к окончательным выводам, имеется математическая теория, которая объясняет склонность цикад к простым числам. Сперва несколько фактов. В лесу может быть только один выводок цикад, так что объяснение не касается совместного использования ресурсов несколькими выводками. Почти каждый год где-либо в Соединенных Штатах появляется выводок цикад с циклом, составляющим простое число лет. Но в 2009 и 2010 гг. цикад не было. Напротив, в 2011 г. на юго-востоке США было массивное нашествие цикад с 13-летним циклом. (Кстати, 2011 является простым числом, но все же я не думаю, что цикады настолько умны.)
Лучшая на сегодняшний день теория простых чисел, лежащих в основе цикла цикад, исходит из возможного существования хищника, который также периодически появляется в лесу. Появление хищника приходится на время нашествия цикад, и он пирует, поедая насекомых. Но тут в дело вступает естественный отбор, потому что цикады, которые регулируют свою жизнь, исходя из цикла, составляющего простое число лет, будут значительно реже сталкиваться с хищниками, чем цикады с жизненным циклом, не представляющим простое число.
Предположим, например, что хищники появляются каждые 6 лет. Цикады с 7-летним циклом будут совпадать с хищниками лишь раз в 42 года. В отличие от них цикады с 8-летним циклом будут появляться одновременно с хищниками каждые 24 года; у цикад же с 9-летним циклом совпадение будет еще чаще – каждые 18 лет.

Рис. 1.02. Взаимодействие на протяжении 100 лет между популяциями цикад с 7-летним жизненным циклом и хищников с 6-летним
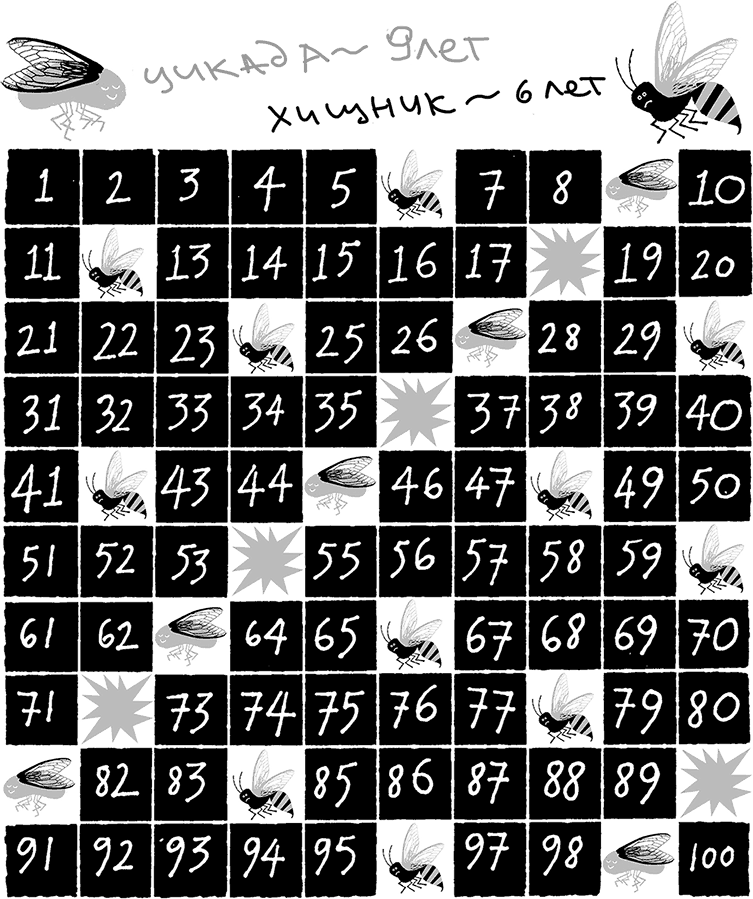
Рис. 1.03. Взаимодействие на протяжении 100 лет между популяциями цикад с 9-летним жизненным циклом и хищников с 6-летним
В лесах Северной Америки было, по-видимому, настоящее соревнование, чтобы найти наибольшее простое число. Цикады настолько преуспели в этом, что хищники либо вымерли, либо переселились, оставив цикад с их странным жизненным циклом в простое число лет. Но, как мы вскоре увидим, не только цикады научились использовать синкопированный ритм простых чисел.
Цикады против хищников
Скачайте PDF-файл с веб-сайта «Тайн 4исел». Вырежьте хищников и два семейства цикад. Положите хищников на годы, кратные 6. Каждый игрок берет по семейству цикад. Возьмите три обычные игральные кости с шестью гранями. Сумма чисел, выпавших на трех игральных костях, определит, как часто появляется ваше семейство цикад. Так, если у вас выпало 8, поместите цикаду на каждое число, кратное 8. Но, если на данном месте уже есть хищник, вы не можете разместить там цикаду, например, не можете положить цикаду на 24, потому что это число уже занято хищником. Победителем будет игрок с наибольшим числом цикад на поле. Вы можете модифицировать игру, изменив периодичность, с которой появляется хищник, то есть вместо 6 выбрать другое число.
Назад: Должен ли вратарь мадридского «Реала» играть в футболке с номером 1?
Дальше: Отчего простые числа 17 и 29 являются ключом к концу времени?

