Книга: Тайны чисел: Математическая одиссея
Назад: Как математика может вам помочь попасть в Книгу рекордов Гиннесса?
Дальше: Решения
Как премьер-лига может принести вам «математический миллион»?
В середине сезона ваша команда томится в нижней половине турнирной таблицы, и вы хотите понять, остались ли у нее математические шансы стать чемпионом. Интересно, что математика, лежащая в основе попыток ответа на данный вопрос, напрямую связана с задачей на миллион долларов этой главы.
Чтобы разобраться, возможно ли это математически, вы начинаете с предположения, что ваша команда выиграет все оставшиеся матчи. Это даст ей три очка за каждую игру. Проблемы начинаются, когда вы пытаетесь проследить за необходимым распределением всех остальных очков в турнирной таблице. Вы желаете достаточного количества проигрышей командам, находящимся выше, чтобы ваша команда обошла их. Но не получится так, чтобы все проигрывали, ведь другие команды играют и между собой. Значит, вам необходимо найти правильный способ распределения очков в оставшихся матчах и надеяться, что одна из допустимых комбинаций выведет вас наверх таблицы. Наверняка должен быть более элегантный способ определить, существует ли такая выигрышная комбинация.
Вам необходимо найти хитроумный прием наподобие того, который использовал Эйлер для рисования карт, – он означал бы, что вам не требуется разбирать все возможные сценарии результатов предстоящих матчей. К несчастью, в настоящее время мы не знаем, существует ли такой прием. Миллион долларов получит первый человек, который либо найдет этот прием, либо докажет, что у этой задачи есть некоторая неотъемлемая сложность, из-за которой полный перебор является единственной возможностью решить задачу.
Любопытно, что до 1981 г. существовала эффективная программа, которой вы могли воспользоваться в середине сезона для проверки того, остается ли у вашей команды шанс выиграть премьер-лигу. До 1981 г. команде присуждались лишь два очка за победу, и эти же два очка делились между соперниками в случае ничьей. Это очень существенно с математической точки зрения, поскольку означает, что полное число очков, разыгранных в сезоне, фиксированно. Например, в лиге с 20 командами, такой как премьер-лига, каждая команда играет 38 матчей (один матч дома и один матч на выезде против каждой из остальных 19 команд). Итак, получается 20 × 38 матчей… за исключением того, что я учел каждый матч дважды. Ведь матч «Арсенала» против «Манчестер Юнайтед» – это также матч «Манчестер Юнайтед» против «Арсенала». Итак, в общей сложности получается 10 × 38 = 380 матчей. Система подсчета очков, применявшаяся до 1981 г., означала, что полное количество очков в конце сезона будет равняться 2 × 380 = 760, и эти очки будут распределены между 20 командами. Это обстоятельство было ключевым для эффективной программы, которой можно было воспользоваться в середине сезона, чтобы понять, остался ли у вашей команды шанс выиграть титул.
В 1981 г. все изменилось математически. Когда за победу даются три очка и в общей сложности два очка за ничью (по одному каждой из команд), нельзя сказать заранее, каким будет полное количество очков в конце сезона. Если каждый матч завершится вничью, то полное количество очков будет снова 760. Но если в каждом матче будет победитель, то полное количество очков будет 1140. Это изменение сделало задачу о премьер-лиге трудноразрешимой.
Имеется множество иных вариантов задачи о премьер-лиге, за которые можно взяться, если вы не футбольный болельщик. Классический вариант называется задачей коммивояжера. В качестве примера такой задачи разберитесь со следующим: вы коммивояжер, и вам необходимо посетить 10 клиентов, причем все они находятся в разных городах. Эти города соединены дорогами, как показано на приведенной карте, – но топлива у вас хватит лишь на 238 миль.
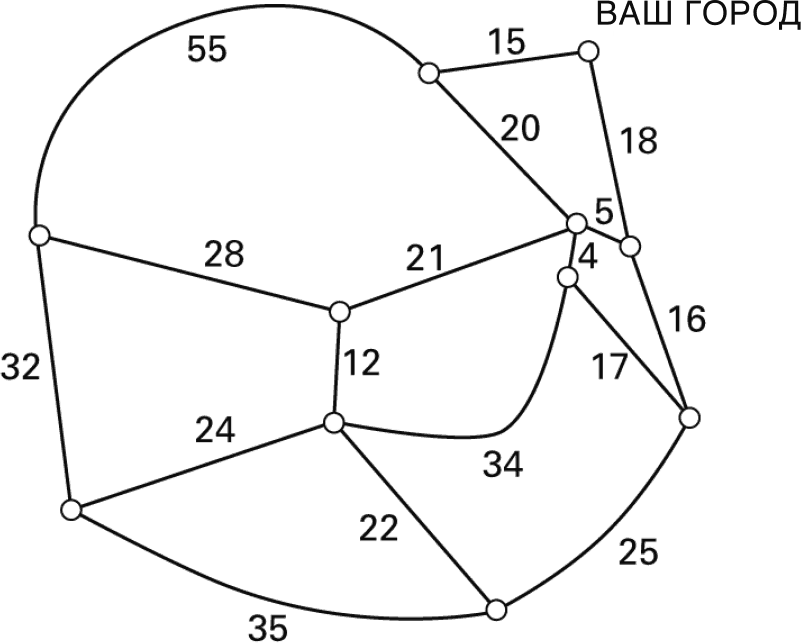
Рис. 3.17. Пример задачи коммивояжера. Можете ли вы найти маршрут протяженностью 238 миль или менее, который проходит через все точки на карте и возвращается в начальную точку?
Расстояние между городами задается числом на дороге, соединяющей их. Можете ли вы найти маршрут, позволяющий вам посетить всех 10 клиентов и затем вернуться домой на имеющемся топливе? (Решение приведено в конце главы.) В данной версии задачи миллион предлагается тому, кто найдет общий алгоритм или напишет компьютерную программу, которая выдаст кратчайший путь для любой задаваемой карты и будет при этом существенно быстрее перебора всех вариантов. Число возможных маршрутов экспоненциально растет с ростом числа городов, поэтому поиск методом полного перебора вскоре становится практически невозможен. Или же вы сумеете доказать, что такой быстрой программы не может быть?
Среди математиков преобладает мнение, что задачи этого вида имеют встроенную сложность, что означает отсутствие какого-то умного способа для поиска решения. Я обычно называю эти задачи иголкой в стоге сена, потому что, по существу, имеется много возможных решений, и вы стараетесь найти особенное из них. Техническое название для них – NP-полные задачи.
Как только вы нашли иголку, легко проверить, что она является требуемым результатом, – это одна из ключевых характеристик данных головоломок. Например, вы понимаете, что задача решена, как только вы нашли маршрут на карте, не превосходящий 238 миль. Подобным образом, если вы находите нужную комбинацию результатов на остаток футбольного сезона, вы мгновенно видите, что у вашей команды еще остается математическая возможность стать чемпионами. Задачами класса P в математике называют те, для которых существуют эффективные программы по поиску решения. Задача на миллион долларов может быть сформулирована так: являются ли NP-полные задачи в действительности задачами класса P? Математики говорят об этом как о соотношении классов P и NP.
Имеется другое любопытное свойство, связывающее все NP-полные задачи. Если вы найдете эффективную программу для одной из задач, это будет означать существование таких программ для всех остальных задач. Например, если вам удастся написать умную программу, которая будет выдавать коммивояжеру кратчайший путь, ее можно будет переделать в эффективную программу проверки того, может ли еще ваша команда стать чемпионом. Чтобы дать пример того, как это может сработать, рассмотрим две задачи из класса «иголка в стоге сена», или NP-полных задач, которые кажутся совершенно разными.
Задача о дипломатичном званом обеде
Вы хотите пригласить ваших друзей на званый обед, но некоторые из них на дух не переносят друг друга и вы не хотите, чтобы два врага оказались в одной комнате. Тогда вы решили организовать три обеда и пригласить на них разных людей. Сумеете ли вы написать приглашения так, что два врага не окажутся за одним столом?
Задача о раскраске карты тремя цветами
В главе 2 мы узнали, что карту всегда можно раскрасить с помощью четырех цветов. Но существует ли эффективный прием, позволяющий сказать, что для заданной карты можно обойтись тремя красками?
Но как решение задачи о трех красках может помочь вам в задаче о званом обеде? Давайте предположим, что вы записали имена своих друзей и соединили линиями пары людей, которые ненавидят друг друга:
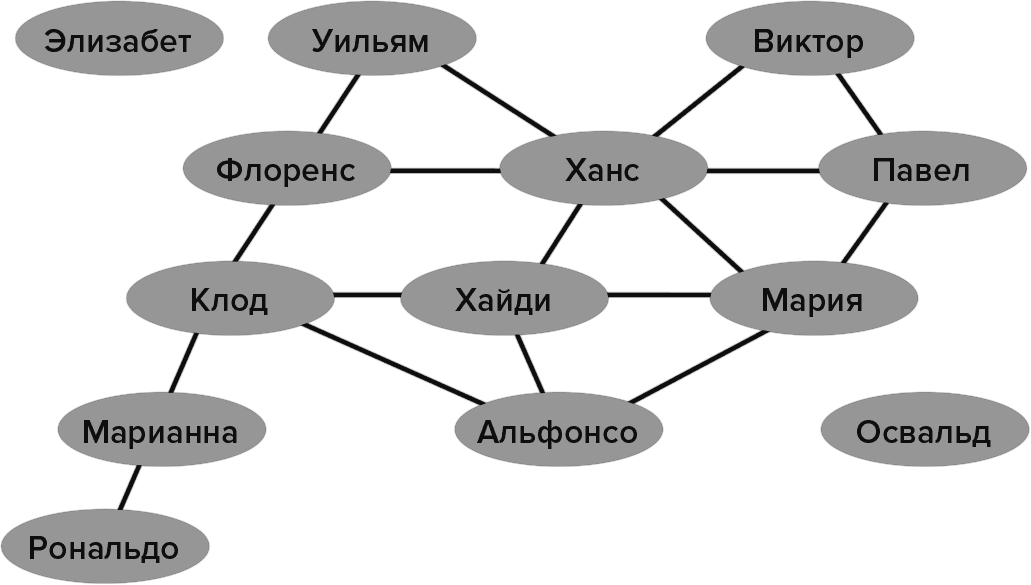
Рис. 3.18. Линией соединены люди, которых нельзя пригласить на один обед
Чтобы решить, на какой из обедов вы должны пригласить того или иного друга, вы могли бы начать раскрашивать овалы вокруг имен разными цветами, причем разные цвета соответствуют разным званым обедам. Следовательно, решение о том, состоится ли обед, определяется тем, удастся ли раскрасить рисунок выше так, что никакие два имени, соединенные линией, не были бы окрашены в один цвет. Но посмотрите, что произойдет, если вы замените имена друзей чем-то другим (рис. 3.19).
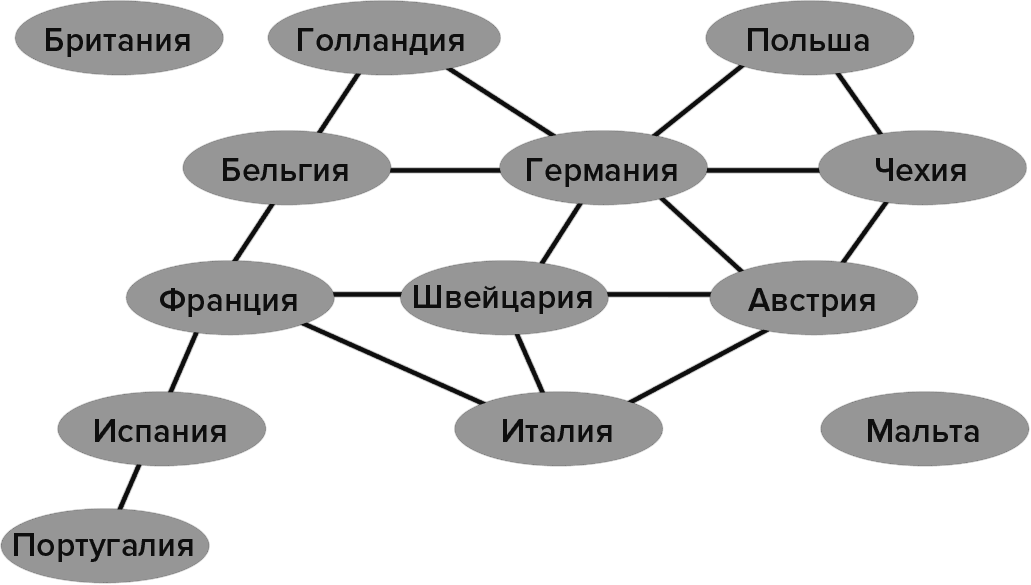
Рис. 3.19. Линией соединены страны, имеющие общую границу
Ваши друзья, которые не любят друг друга, стали европейскими странами, и линии, соединяющие их, обозначают наличие общей границы. Задача о том, на какую из трех вечеринок пригласить того или иного друга, стала задачей о выборе одного из трех цветов для раскраски той или иной страны на карте Европы. Вопросы об организации званых обедов и раскраски карты тремя цветами являются различными версиями одного и того же вопроса, так что, если вы найдете эффективный способ решения одной из NP-полных задач, вы придете к решению их всех! Предлагаю вам на выбор несколько разных задач, на которых вы можете попробовать свои силы с целью выигрыша миллиона.
Сапер
Это компьютерная игра для одного участника, которая имеется в каждом установочном комплекте операционной системы Microsoft. Цель игры состоит в том, чтобы очистить сетку от мин. Если вы щелкаете по квадратику на сетке, и там нет мины, то появляется число, показывающее, во скольких квадратиках вокруг данного есть мины. Если же вы щелкаете по мине… то взлетаете на воздух. Но саперный вызов на миллион долларов предлагает вам сделать несколько иное. Следующий рисунок не может появиться в настоящей игре, потому что никакое расположение мин не может дать такие числа (рис. 3.20). Число 1 означает, что лишь в одном из неоткрытых квадратиков есть мина, а число 2 означает, что заминированы оба.
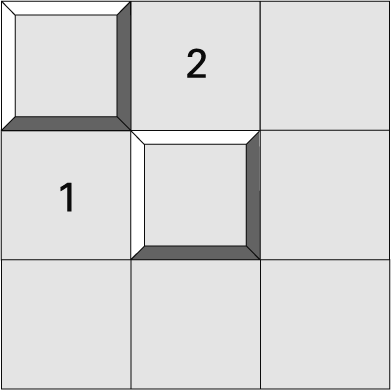
Рис. 3.20
Но что можно сказать о следующем рисунке – можно ли увидеть такой в настоящей игре?

Рис. 3.21
Существует ли возможность разместить мины так, чтобы появились эти числа? Или же данный рисунок никоим образом не может возникнуть в настоящей игре, потому что не существует расположения мин, совместимого с этими числами? Ваша задача состоит в том, чтобы разработать эффективную программу, которая сумеет дать ответ на этот вопрос для какой угодно картинки.
Задача об упаковке
Вы руководите фирмой по переезду. Все ваши упаковочные ящики имеют одинаковую ширину и высоту, совпадающие с внутренними размерами вашего грузовика (ну, или чуть меньше этих размеров, так, чтобы их можно было разместить внутри). Но длина ящиков разная. Длина вашего грузовика 150 футов, а у имеющихся ящиков следующие длины: 16, 27, 37, 42, 52, 59, 65 и 95 футов.
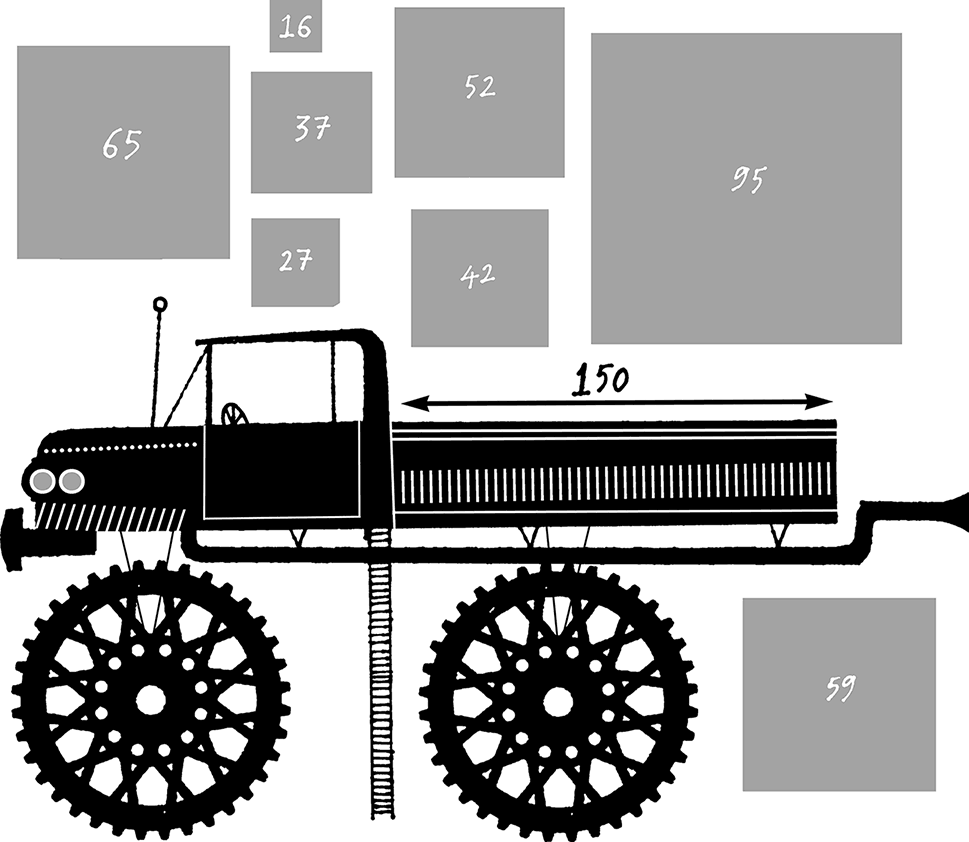
Рис. 3.22. Упаковка коробок является математически сложной задачей
Можете ли вы найти комбинацию ящиков, которая наполнит грузовик самым эффективным способом? Вы должны найти алгоритм, определяющий для любого заданного числа N и набора меньших чисел n(1), n(2), …, n(r), существует ли набор меньших чисел, складывающийся в большее число.
Судоку
Нахождение эффективной программы для решения сколь угодно больших головоломок судоку является NP-полной задачей. Иногда судоку бывают настолько убийственны, что приходится делать некоторые предположения и потом исследовать логические последствия этих предположений. Не представляется возможным существование какого-то эффективного способа делать эти предположения, иначе чем перебирать различные наборы предположений, пока не получится последовательный ответ.
Такого рода задачи не являются просто играми: они возникают в бизнесе и промышленности, когда компаниям необходимо найти самое эффективное решение какой-то практической проблемы. Незанятое пространство или перерасход топлива влекут денежные потери, и менеджерам часто приходится решать одну из этих NP-задач. В телекоммуникационной промышленности даже используются коды, дешифровка которых зависит от того, удается ли найти иголку в стоге сена. Поэтому не только математики или заядлые игроки заинтересованы в решении этой задачи на миллион долларов.
Будь то математический анализ футбольных игр или организация званых приемов, раскрашивание карт или расчистка минных полей – задача на миллион долларов из этой главы появляется в столь разнообразных обличьях, что вы наверняка сумеете найти привлекательный для себя вариант. Но имейте в виду следующее: эта задача может казаться забавной и игровой, тем не менее она – одна из самых трудных задач на миллион долларов. Математики полагают, что во всех этих задачах имеется некая существенная сложность, из-за чего может не найтись эффективной программы для их решения. К сожалению, всегда оказывается труднее показать, почему что-то не существует, чем показать его существование. Но, по крайней мере, для вас может быть забавно попытаться получить миллион этой главы.

