В 1979 г. компьютерная компания Atari выпустила свою самую популярную видеоигру «Астероиды». Ее целью было подбить и уничтожить астероиды и летающие тарелки, одновременно уклоняясь от пролетающих астероидов и ответного огня летающих тарелок. Аркадная версия игры была настолько успешна, что в США потребовалось устанавливать в игровые автоматы бо́льшие контейнеры, чтобы вместить возросший поток 25-центовых монет.

Но с математической точки зрения интерес представляет геометрия игры: как только космический корабль пересекает верх экрана, он волшебным образом появляется внизу. Подобным образом при пересечении экрана слева космический корабль снова появляется на экране справа. Получается так, что наш космонавт заперт в двумерном мире, и вселенная целиком видна на экране. Хотя эта вселенная конечна, у нее нет границ. Поскольку космонавт никогда не доходит до края, он живет не внутри прямоугольника, а перемещается в более интересной вселенной. Можем ли мы понять, какова ее форма?

Если космонавт выходит с экрана наверху и снова появляется внизу, то эти части вселенной должны быть соединены. Представьте, что компьютерный экран сделан из гибкой резины, так что мы можем согнуть его и соединить верх с низом. Теперь мы видим, что, когда космонавт летит по экрану вертикально, он на самом деле кружится и кружится по цилиндру.

А что происходит в другом направлении? После того как космонавт исчезает с экрана слева, он снова появляется справа, поэтому два конца цилиндра также должны быть соединены. Если мы отметим точки, где они соединяются, то поймем, что цилиндр нужно согнуть и совместить его основания. Итак, в действительности наш космонавт живет на поверхности бублика, или на торе, как называем ее мы, математики.

С помощью этого куска резины я проиллюстрировал новый способ глядеть на формы, который появился в математике примерно сто лет назад. Для древних греков смысл геометрии (что буквально означает на греческом «измерение земли») состоял в определении углов и расстояний между точками. Но при анализе формы вселенной космонавта из игры «Астероиды» главными для нас были не расстояния, а то, как части формы соединены друг с другом. Этот новый взгляд на формы, когда разрешается сжимать и растягивать их, словно они сделаны из резины или пластилина, называется топологией.

Многие люди используют топологические карты каждый день. Узнаёте карту, показанную ниже? Это геометрическая карта лондонского метро, но она не слишком удобна для ориентирования, хотя и точна географически. Вместо нее лондонцы используют топологическую карту. Ее придумал Гарри Бек в 1933 г. – он сжимал и растягивал геометрическую карту, чтобы получить удобную в пользовании схему метро. Ее аналоги теперь распространены по всему миру.

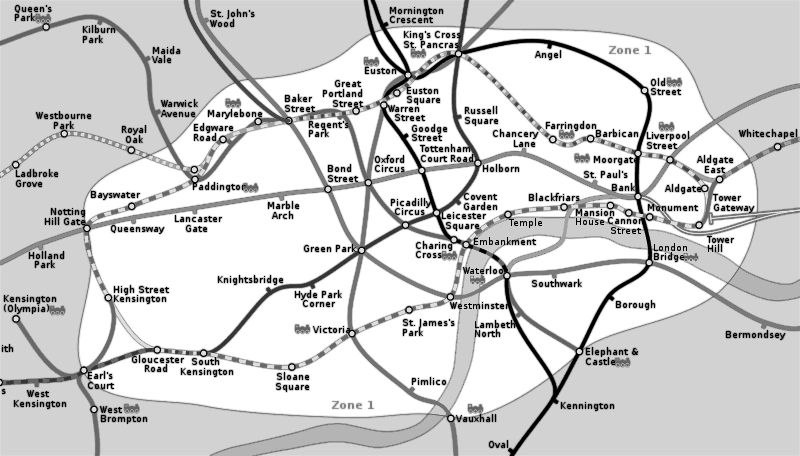
Рис. 2.38. Геометрическая карта лондонского метро

Вопрос о том, можно ли развязать узел, также является топологическим, потому что при этом мы можем тянуть за веревки, но не разрезать их. Данный вопрос имеет фундаментальное значение для биологов и химиков, потому что человеческая ДНК стремится образовывать странные узлы. Некоторые болезни, например болезнь Альцгеймера, возможно, связаны с тем, как запутывается ДНК, и у математиков есть потенциал для разгадки их тайн.

В начале XX в. французский математик Анри Пуанкаре задался вопросом о том, сколько имеется топологически различных поверхностей. Это соответствует нахождению всех возможных форм, на которых мог бы жить наш двумерный космонавт из игры «Астероиды». Пуанкаре интересовался этими вселенными с топологической точки зрения, поэтому две вселенные должны считаться одинаковыми, если одну из них можно деформировать в другую непрерывным образом, не делая разрезов. Например, двумерная сфера топологически эквивалентна двумерной поверхности мяча для игры в регби, потому что одну можно преобразовать в другую. Но эта сферическая вселенная топологически отлична от тора, по которому летает двумерный космонавт, потому что сферу нельзя деформировать в бублик, не делая в ней разрезов или склеек. Но какие другие формы имеются?

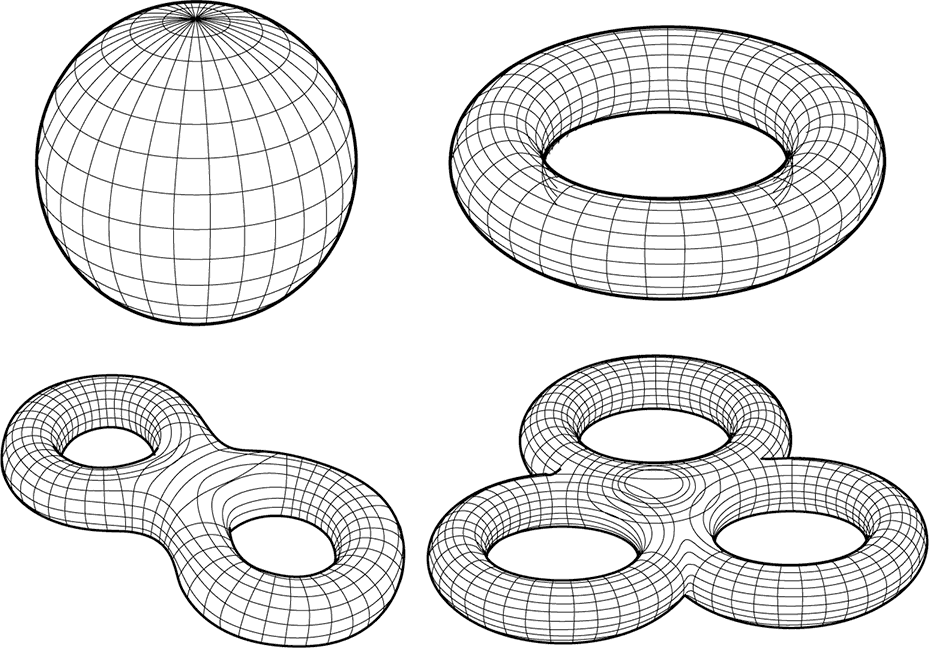
Рис. 2.39. Первые четыре формы в топологической классификации двумерных поверхностей, предложенной Анри Пуанкаре

Пуанкаре сумел доказать, что, какой бы сложной ни была форма, ее всегда возможно деформировать непрерывным образом в одну из следующих форм: сферу, тор с одной дыркой, тор с двумя дырками либо тор с любым конечным числом дырок. С топологической точки зрения это полный список всех возможных вселенных для нашего двумерного космонавта. Именно количество дырок – которое математики называют родом поверхности – характеризует форму. Так, чайная чашка топологически эквивалентна бублику, потому что у них по одной дырке. У чайника же две дырки, одна в носике, а другая в ручке, и его можно преобразовать так, чтобы он выглядел как брецель с двумя дырками. Наверное, необходимы большие усилия, чтобы понять, почему форма на рис. 2.40, в которой также две дырки, может быть деформирована в брецель с двумя дырками. Кажется, что из-за зацепления бубликов потребуется разрезать форму, чтобы успешно деформировать ее, но это не так.

Рис. 2.40. Как расцепить два кольца, непрерывно деформируя их, но не делая разрезов?

В конце главы я объясню, как расцепить кольца, не разрезая.