Криптография в совершенном мире

Что станет с криптографией в совершенном мире? В мире из второй главы, где P = NP? Определить, что число 16461679220973794359 представляется в виде 5754853343 × 2860486313, а числа 5754853343 и 2860486313 – простые, не составит особого труда; подобные вычисления можно будет проделывать с числами из тысяч и даже миллионов цифр! Задача разложения на множители лежит в классе NP, поскольку потенциальное решение можно проверить очень быстро; если классы P и NP совпадают, то для этой задачи существует эффективный алгоритм, а значит, мы легко отыщем все делители любого, сколь угодно большого числа. Протокол RSA, как и любая другая система шифрования с открытым ключом, станет абсолютно бесполезен, поскольку закрытый ключ будет быстро восстанавливаться по открытому ключу. Равенство P и NP приведет к тому, что мы больше не сможем обмениваться секретной информацией, не условившись предварительно о способе ее передачи.

Так, значит, в совершенном мире о криптографии придется забыть? Вообще-то есть один шифр, надежность которого не зависит от отношений между P и NP: это так называемый одноразовый шифровальный блокнот. Предположим, Элис придумала пароль из 12 символов: FIDDLESTICKS. Шифровальный ключ – он же блокнот – представляет собой случайную последовательность символов той же длины: JXORMQNAMRHC. Возьмем первые символы пароля и ключа, F и J. Это шестая и десятая буквы алфавита, соответственно. В сумме их номера дают число 16, поэтому первым символом шифрованного текста будет шестнадцатая буква алфавита – P. Теперь возьмем вторые символы пароля и ключа, I и X. Это девятая и двадцать шестая буквы алфавита. В сумме их номера дают 33, однако тридцать третьей буквы алфавита в английском языке не существует, поэтому мы вычитаем из числа 33 количество букв в алфавите, т. е. 26. Получается 7, а значит, вторым символом шифровки будет седьмая буква алфавита – G. Действуя аналогичным образом, мы в итоге получим PGSVYVGUVUSV. Эту криптограмму Элис отошлет на Facebook, а он расшифрует ее с помощью точно такого же блокнота, выполняя вычитание вместо сложения.

Любая строка длины 12 может быть ключом. Любая строка длины 12 может быть исходным сообщением. Все варианты равновероятны, так что, имея на руках криптограмму, получить какую-либо информацию об исходном тексте абсолютно невозможно. Этот факт математически доказан, и классы P и NP тут совершенно ни при чем. Но тогда зачем нужны все эти хитроумные и потенциально уязвимые системы шифрования, завязанные на поиск простых сомножителей? Почему бы нам не перейти на одноразовые блокноты?

К сожалению, с блокнотами все обстоит не так просто. Их ведь потому и назвали одноразовыми, что любой ключ разрешается использовать только один раз. Это правило должно соблюдаться неукоснительно; даже если два не связанных между собой человека отсылают сообщения двум другим не связанным между собой людям, лучше, чтобы их ключи не совпадали, иначе конфиденциальность переписки может быть нарушена. Кроме того, одноразовый блокнот обязательно должен быть той же длины, что и сообщение. В отличие от криптосистем с открытым ключом, ключ здесь лишь один – секретный, общий для обеих сторон. И Элис, и Facebook должны знать секретный ключ; если к злоумышленнику попадет хотя бы часть ключа, он сможет получить некоторую информацию об исходном сообщении, поэтому Facebook должен переправить Элис ключ так, чтобы его никто, кроме самой Элис, не увидел (или наоборот – Элис должна переправить ключ в Facebook). Данные, пересылаемые по интернету, легко перехватить. Блокноты нужно передавать на физическом носителе, например – на флешке, причем делать это только лично или через надежного посредника. В совершенном мире Элис, скорей всего, отправилась бы в ближайший супермаркет и купила запечатанную флешку с набором одноразовых блокнотов. Производством таких флешек занималась бы заслуживающая доверия организация (возможно, правительство), способная гарантировать безопасную передачу второго экземпляра блокнота в Facebook и другие подобные компании.

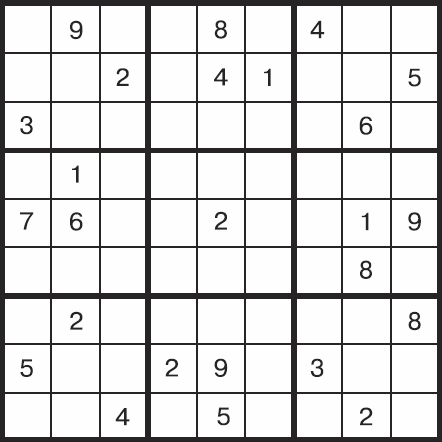
Рис. 8.6. Судоку с нулевым разглашением

Равенство P = NP многое упрощает, однако криптографам оно может принести лишь головную боль.

Создавать и передавать одноразовые блокноты можно и при помощи квантовой механики. Правда, это очень дорого, так что в широких масштабах такой подход применяться не будет. Подробнее о квантовой криптографии мы поговорим в следующей главе.

Судоку с нулевым разглашением

Боб пожертвовал обедом, чтобы добить судоку из последнего номера газеты.

«У них тут ошибка. Это решить невозможно!» – восклицает он, совершенно выбившись из сил. На крики приходит его коллега Элис; взглянув на судоку, она видит ту самую головоломку, которую утром решила в метро. Боб зря ругается. На рисунке ниже вы видите решение Элис.

Боб вот-вот сдастся, и Элис хочется его поддержать. Она говорит, что решила задачу, но он ей, конечно, не верит. Он ужасно расстроится, когда увидит в завтрашней газете ответ, так что нужно обязательно убедить его подумать еще. Показать свое решение значит испортить Бобу все удовольствие от процесса; но как доказать, что задача решается, не давая при этом никаких подсказок?

Рис. 8.7. Решение судоку с нулевым разглашением

К счастью, в колледже Элис специализировалась на теоретической информатике и поэтому знает о доказательствах с нулевым разглашением. В голове у нее быстро созревает план действий.

Вернувшись к своему столу и зная, что Боб не может видеть ее за перегородкой, Элис берет цифры от 1 до 9 и случайным образом их упорядочивает.

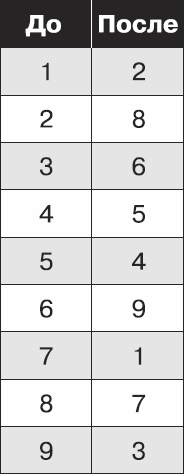
Рис. 8.8. Новый порядок цифр

С помощью полученной таблицы Элис шифрует свое решение, заменяя 1 на 2, 9 на 3, и т. д., и рисует его на большом листе бумаги. Вот что у нее выходит:

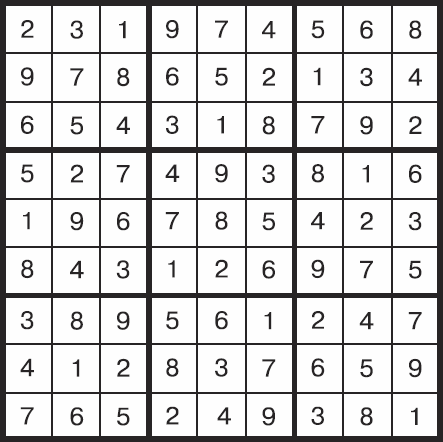
Рис. 8.9. Зашифрованное решение

Дальше Элис аккуратно режет сетку с решением на маленькие квадратики по одной цифре в каждом. Всего квадратиков получается 81. Каждый квадратик она прячет в маленький пакетик и кладет в соответствующую ячейку нарисованной на другом листе пустой сетки.

Рис. 8.10. Решение спрятано

Рис. 8.11. Открытая строка

В левом верхнем пакетике лежит цифра 2, справа от него – цифра 3, и так далее.

Осторожно, без резких движений, Элис относит всю эту конструкцию Бобу и объясняет ему, что именно она сделала. Не раскрывая схему кодировки цифр, она предлагает провести тест. Бобу разрешается выбрать один из двадцати восьми вариантов:

• открыть все пакетики в одной из строк;

• открыть все пакетики в одном из столбцов;

• открыть все пакетики в одном из девяти блоков 3 × 3;

• открыть все пакетики, расположенные на тех же позициях, что и заданные цифры исходной головоломки.

Допустим, Боб решил открыть третью строку. Что он там увидит?

Если бы в строке оказалось две одинаковых цифры, это означало бы, что Элис наврала. Но поскольку решение у нее действительно есть, и она четко объяснила Бобу, что сделала с пакетиками, Боб видит все различные цифры от 1 до 9 в случайном порядке. Тест пройден!

Если Боб решит открыть столбец или блок 3 × 3, результат будет точно таким же.

Теперь предположим, что он выберет последний вариант – «открыть все пакетики, расположенные на тех же позициях, что и заданные цифры исходной головоломки». Открыв пакетики, Боб видит такую картину.

Рис. 8.12. Открытые позиции соответствуют заданным цифрам

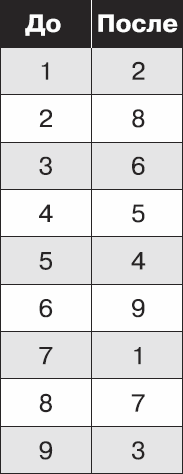
Рис. 8.13. Новый порядок цифр

Это единственный случай, когда Боб получает от Элис еще и таблицу кодировки, при помощи которой он проверит, соответствуют ли открытые цифры тем, что были указаны в задаче изначально. Например, согласно схеме, цифра 9 должна была превратиться в цифру 3… так и есть!

Если Элис и правда решила задачу и четко следовала правилам, она пройдет любую проверку. А что же Боб? Получит ли он хоть какую-нибудь подсказку, когда откроет строку, столбец или блок 3 × 3? Исключено: перед ним будут лишь цифры от 1 до 9, расположенные в случайном порядке.

Последний вариант даст ему перестановку цифр, при помощи которой было зашифровано решение. Но что он при этом узнает? Ничего.

Другое дело, если Элис наврала: один из тестов обязательно провалится, и она ничего не сможет с этим поделать. Когда Боб выбирает тест наугад, вероятность попасться на вранье составляет одну двадцать восьмую, или примерно 3,57 %. Не так уж и рискованно, правда? Однако если Элис и Боб проведут 83 эксперимента подряд и при этом будут каждый раз менять схему кодировки, вероятность провалить один из тестов возрастет до 95 %.

Боб убедился, что Элис действительно решила судоку, а ей при этом удалось соблюсти принцип «нулевого разглашения»: о решении Боб знает только то, что оно существует. Эта мысль будет греть его, когда он вернется к головоломке, но справляться ему придется исключительно своими силами.

Мы исходили из предположения, что Боб не хочет слышать никаких подсказок. На случай, если он решит сжульничать и открыть сразу все пакетики, Элис может спрятать цифры в запирающиеся коробочки и по мере необходимости выдавать Бобу ключи.

Теперь представим, что Боб и Элис не работают вместе и вообще находятся в разных городах. Они могут связаться по телефону или электронной почте, однако вместо пакетиков придется придумать что-то другое. Здесь на помощь им придет несложный шифр. Каждому пакетику Элис может присвоить уникальный номер – большое случайное число, последняя цифра которого совпадает с цифрой внутри. Для цифры 2 подойдет, к примеру, 3682502. Затем она зашифрует номера пакетиков своим открытым ключом и отошлет их Бобу. Когда Боб определится с вариантом теста, Элис сообщит ему исходные номера тех пакетиков, которые разрешается открыть. Для проверки Боб повторно зашифрует их открытым ключом и получит те же номера, что Элис выслала ему в начале.

В четвертой главе мы уже упоминали, что решение судоку – задача NP-полная. А раз к судоку сводится любая задача из NP, то и описанный выше метод доказательства с нулевым разглашением также годится для любой NP-задачи. Элис сможет убедить Боба в том, что она нашла максимальную клику, раскрасила карту в три цвета или составила маршрут для коммивояжера, не раскрывая при этом никакой дополнительной информации; о решении Боб будет знать только то, что оно существует.

Классический способ осуществить криптографическую атаку – выдать себя за другого. Защититься от самозванцев помогает доказательство с нулевым разглашением. Происходит это так. Элис выбирает любой известный только ей секрет и шифрует его своим открытым ключом. Ее цель – убедить Боба, что она и вправду Элис. Она, конечно, может отправить ему зашифрованный текст, но тогда Боб получит возможность выдавать себя за нее. Так что Элис проводит доказательство с нулевым разглашением и показывает Бобу, что действительно владеет секретной информацией. В результате Боб верит, что общается именно с Элис, но при этом ничего не знает о ее секрете.