Иголка в стоге сена

Предположим, мы ищем клику из трех человек среди всех 20000 жителей Королевства. По самым грубым подсчетам нужно проверить чуть больше триллиона вариантов – сущая ерунда для любого современного компьютера. Однако дальше варианты начинают размножаться с космической скоростью, перед которой компьютеры очень быстро пасуют: для клики размера четыре требуется уже 6 квадриллионов проверок, для клики размера пять – 26 квинтиллионов, а для клики размера шесть – 88 секстиллионов (т. е. 88 и 21 ноль).

Впрочем, поиск «иголки в стоге сена» не всегда превращается в такую катастрофу. Группа жителей Королевства считается очень приятной, если для любой пары друзей хотя бы один из них в эту группу входит.

Рис. 6.8. Дружеские связи

На представленной выше диаграмме Боб, Даниэль, Фрэнк и Гарри образуют очень приятную группу, поскольку все дружеские связи (линии на схеме) завязаны на них.

Рис. 6.9. Очень приятная группа размера четыре

А вот очень приятную группу размера три составить уже не получится. Например, если взять Элис, Чарли и Фрэнка – потеряются дружеские связи Ева – Даниэль и Джордж – Гарри.

Задача поиска очень приятной группы, более известная под официальным названием «задача о вершинном покрытии», принадлежит к «старой гвардии» и упоминается еще в списке NP-полных задач Карпа.

Давайте взглянем на дружеские связи Фрэнка. Если Фрэнк не является членом очень приятной группы, то тогда в нее должны входить Джордж, Даниэль и Ева, поскольку все они с Фрэнком друзья. Каждая очень приятная группа обязательно содержит либо Фрэнка, либо всех его друзей – даже если их не три, а целых сто.

При помощи подобных хитростей можно избежать полного перебора всех потенциальных вариантов при поиске небольших очень приятных групп. Для группы размера пять понадобится около 100000 проверок, для группы размера 10–200000 проверок, а для группы размера 30–601000 проверок; любой ноутбук справится с такой задачей за считаные доли секунды. Поиск очень приятной группы размера 113 потребует проверки триллиона вариантов и будет длиться не дольше, чем поиск клики из каких-то несчастных трех человек.

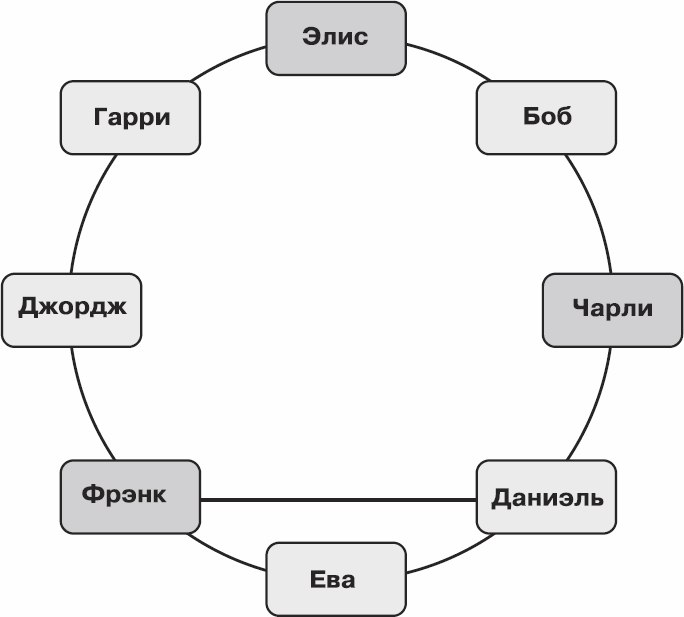
Рис. 6.10. Не очень приятная группа размера 3

Стоп. Выходит, очень приятные группы искать не так уж сложно? Но разве Карп не доказал, что поиск очень приятной группы минимального размера (т. е. минимального вершинного покрытия) – задача NP-полная? Дело в том, что у жителей Королевства друзей обычно очень много. Маловероятно, что все дружеские связи завязаны лишь на 113 жителях. А как только мы замахнемся на группы побольше, число вариантов тут же резко возрастет.

Например, для группы размера 150 потребуется уже 1,5 квадриллиона проверок, для группы размера 200 – более секстиллиона, а для группы размера 500 – примерно 38 сексдециллионов (т. е. 38 и 51 ноль). Поиск очень приятной группы минимального размера – задача практически неразрешимая. А вот если нам просто нужно убедиться, что в Королевстве не существует очень приятной группы размера сто, мы получим ответ за разумное время.

Приближенные методы

Оптимальное решение получается найти далеко не всегда. Очень часто, однако, не самое лучшее решение оказывается вполне удовлетворительным.

Давайте снова обратимся к NP-полной задаче коммивояжера, в которой требуется проложить кратчайший маршрут через заданные города.

Предположим, вы хотите объехать 50 городов. Вам известно, что длина кратчайшего маршрута – 2800000 км. Если вы составите маршрут в 2810000 км, то вряд ли станете надрываться дальше из-за каких-то лишних 10000 км.

С другой стороны, если дорога обходится вам в доллар за километр, и за весь вояж вам заплатят 2805000 долларов, разница будет очень заметна: вы либо заработаете 5000 долларов (уложившись в 2800000 км), либо потеряете (удовлетворившись маршрутом в 2810000 км). Сократите длину пути до 2803000 км – и окажетесь в плюсе, хотя ваш маршрут не будет оптимальным.

Задача коммивояжера NP-полна, поэтому поиск точного решения предположительно затянется на неопределенное время. Зато мы можем построить приближенный маршрут, причем от оптимального он будет отличаться не так уж и сильно. Санджив Арора и Джо Митчелл независимо друг от друга разработали алгоритм, который разбивает карту на более мелкие куски и решает для каждого из них аналогичную задачу, а затем аккуратно склеивает все обратно.

На рисунке ниже вы видите карту Китая, на которой отмечено 71009 городов.

Наложим на карту частую сетку, решим задачу для каждого квадрата в отдельности, а в конце просто соединим все полученные маршруты. Квадраты, в которых оказалось слишком много городов, можно будет раздробить аналогичным образом.

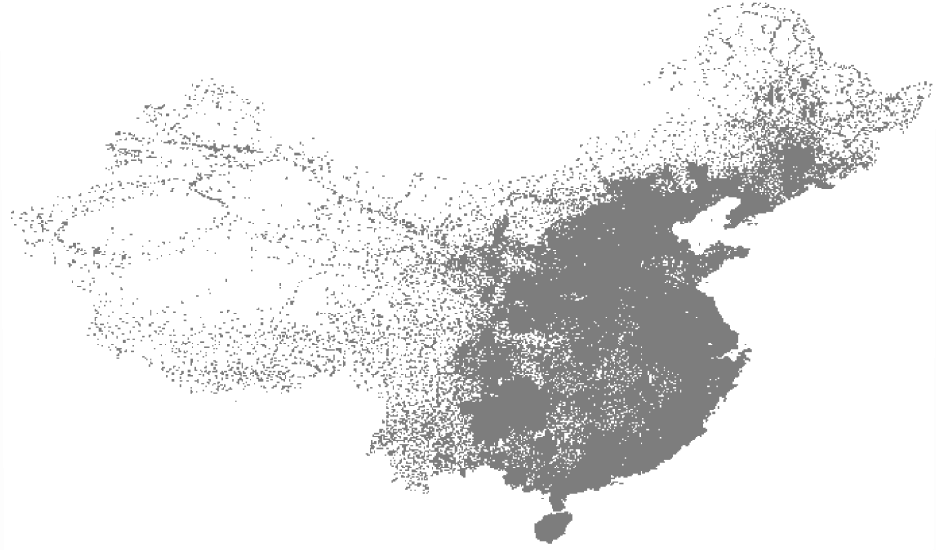
Рис. 6.11. Карта Китая

Этот метод позволяет за разумное время находить коммивояжеру вполне приличные маршруты: длина их отличается от оптимальной всего на несколько процентов.

Если бы все NP-задачи решались приближенными методами настолько замечательно, поднимать вопрос о равенстве или неравенстве P и NP не имело бы особого смысла. Однако в действительности дела обстоят не так уж радужно. Рассмотрим, к примеру, задачу о клике – большой группе людей, в которой все между собой дружны. В общем случае алгоритмы поиска максимальной клики не дают нам хорошего приближения. За разумное время мы вряд ли доберемся даже до клики размера 15; а вдруг в Королевстве есть клика из 2000 жителей?

Если P равно NP, то мы с легкостью отыщем клику любого размера. В противном случае, как выяснилось, нам доступны лишь клики в тысячу раз меньше максимальной. Любой алгоритм, гарантирующий лучшее приближение, позволит находить также и точные решения и докажет равенство P и NP.

Рис. 6.12. Сетка на карте Китая

В большинстве NP-полных задач приближенное решение ищется проще, чем в задаче о клике, но сложнее, чем в задаче коммивояжера. А как обстоит дело с задачей об очень приятных группах?

Мы с вами разобрали тривиальный случай, в котором можно методично перебрать все варианты и убедиться, что минимальная очень приятная группа состоит из четырех человек: Фрэнк, Даниэль, Гарри и Боб. Теперь предположим, что ответ нам неизвестен, и рассмотрим простой приближенный алгоритм поиска очень приятной группы минимального размера.

На первом шаге выберем любых двух друзей и отметим их; пусть это будут Элис и Гарри.

Теперь выберем еще двух друзей, ни один из которых пока не отмечен, и тоже их отметим.

Повторяем до тех пор, пока у нас имеются неотмеченные друзья.

В итоге все те, кого мы отметили, составят очень приятную группу.

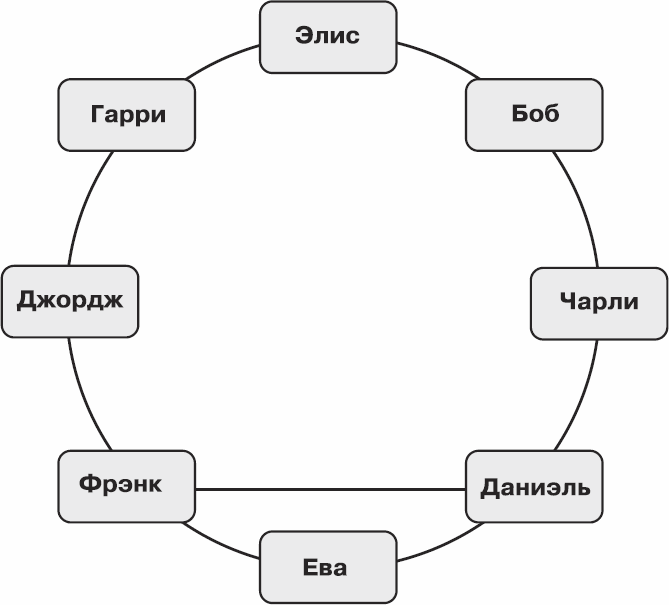
Рис. 6.13. Дружеские связи – II

Рис. 6.14. Поиск очень приятной группы – II: шаг 1

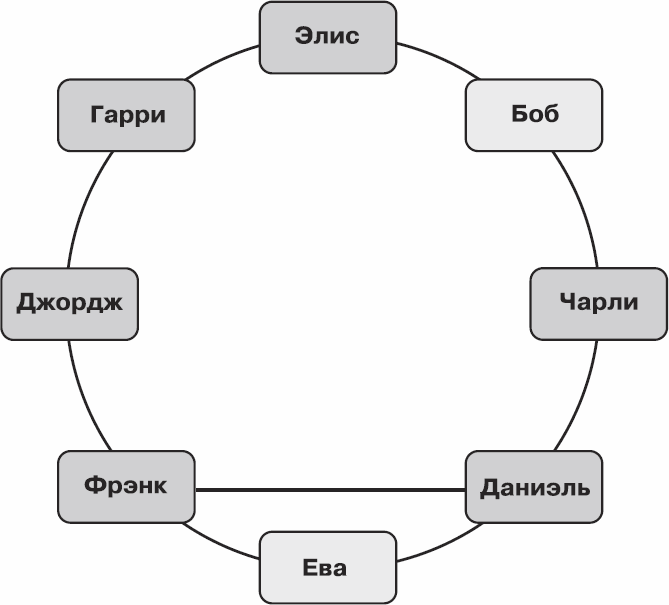
Рис. 6.15. Поиск очень приятной группы – II: шаг 2

Рис. 6.16. Очень приятная группа размера шесть

В нашем случае получилась очень приятная группа размера шесть. Ясно, что любая очень приятная группа содержит хотя бы одного человека из каждой выбранной дружеской пары, а значит – состоит как минимум из трех человек. Поэтому минимальный размер такой группы лежит в промежутке от трех до шести.

Алгоритм подойдет для любой схемы дружеских связей. Если он, к примеру, отберет 50 дружеских пар и построит очень приятную группу из 100 человек, мы будем знать, что минимальный размер группы – от 50 до 100.

Выходит, мы всегда можем найти очень приятную группу, размер которой превышает минимальный не более чем в два раза. Однако существенно улучшить этот результат нам вряд ли удастся.

Если P равно NP, то мы сможем отыскать минимальную очень приятную группу быстро и эффективно. А если не равно? Тогда в общем случае мы будем получать лишь группы, размер которых превышает минимальный более чем на 36 процентов. Любой алгоритм, гарантирующий превышение ровно в 36 процентов или менее, можно преобразовать таким образом, чтобы он решал произвольную NP-полную задачу. Возможность этого преобразования основывается на целом ряде важных и серьезных результатов, полученных в период между 1990 и 2005 годами.

Рассмотренный выше простейший алгоритм последовательного отбора дружеских пар позволяет получить очень приятную группу, размер которой превышает минимальный не более чем в два раза (т. е. не более чем на 100 процентов). Если P ≠ NP, то мечтать о превышении меньше чем в 36 процентов смысла вообще не имеет. Но, может, удастся создать алгоритм, гарантирующий хотя бы 50-процентное превышение?

В поисках ответа на этот и другие вопросы индийский математик Субхаш Кхот разработал свои «уникальные игры» – модификацию задачи о раскраске карт, в которой для раскраски соседних государств вводятся дополнительные правила. Кхот выдвинул гипотезу, что задача об уникальных играх является NP-полной. Так это или нет – пока никто не знает.

Если гипотеза об уникальных играх верна, то у нас нет шансов придумать хороший приближенный алгоритм: из построений Кхота следует, что в этом случае мы не сможем гарантированно находить очень приятные группы, размер которых превышает минимальный менее чем на 100 процентов. Если гипотеза верна, нам останется довольствоваться описанным выше простейшим алгоритмом.