Глава 4: Много шума из ничего

Шаг вперед, два шага назад, похоже, таковы наши поиски понимания Вселенной и придания ей точного облика. Даже несмотря на то, что наблюдения, наконец, окончательно определили кривизну нашей Вселенной — и по ходу проверили давние теоретические подозрения — даже хотя и было известно, что во Вселенной в десять раз больше материи, чем могло бы быть за счет протонов и нейтронов, даже такого огромного количества темной материи, составляющей 30 процентов того, что требуется для получения плоской Вселенной, было далеко недостаточно, чтобы объяснить всю энергию во Вселенной. Прямое определение геометрии Вселенной и последующее открытие, что Вселенная действительно плоская, означало, что 70 процентов энергии Вселенной все еще не хватает, их нет ни внутри, ни вокруг галактик или даже скоплений галактик!

Все было не настолько шокирующим, как я это представил. Еще до этих измерений кривизны Вселенной и определения общей массы скоплений в ней (как описано в главе 2) появились признаки того, что тогдашняя теоретическая картина нашей Вселенной — с достаточным количеством темной материи (как мы теперь знаем, в три раза большим, чем существует на самом деле), чтобы быть пространственно плоской — просто не согласовывалась с наблюдениями. Действительно, еще в 1995 году мы с моим коллегой Майклом Тернером из Университета Чикаго написали еретическую работу, предполагая, что такая условно принятая картина не может быть правильной, и фактически единственная возможность, которая появилась с учетом плоской Вселенной (нашим теоретическим предпочтением в то время) и наблюдений скоплений галактик с их внутренней динамикой, была гораздо более странная Вселенная, которая уходит корнями к сумасшедшей теоретической идее Альберта Эйнштейна, возникшей в 1917 году, чтобы разрешить кажущееся противоречие между предсказаниями его теории и статичной Вселенной, в которой, как он думал, мы жили, и от которой впоследствии он отказался.

Насколько я помню, нашим стремлением в то время было больше показать, что что-то не так с общепринятыми знаниями, чем предложить окончательное решение проблемы. Предположение казалось слишком сумасшедшим, чтобы действительно в него поверить, поэтому я не думаю, что кто-то был более удивлен, чем мы, когда выяснилось, три года спустя, что наша еретическое предположение было все же абсолютно правильным!

Давайте вернемся в 1917 год. Напомню, что Эйнштейн разработал общую теорию относительности, и его сердце переполняла радость, когда он обнаружил, что может объяснить прецессию перигелия Меркурия, даже когда он столкнулся с фактом, что его теория не могла объяснить статичной Вселенной, в которой, по его мнению, он жил.

Если бы у него было больше мужества отстаивать свои убеждения, он мог бы предсказать, что Вселенная не может быть статичной. Но он этого не сделал. Вместо этого он понял, что может сделать небольшое изменение в своей теории, полностью согласующееся с математическими выводами, которые изначально привели его к разработке общей теории относительности, изменение, которое, похоже, делало статичную Вселенную возможной.

Хотя детали сложны, общая структура уравнений Эйнштейна в общей теории относительности относительно проста. Левая сторона уравнений описывает кривизну Вселенной и вместе с тем силу гравитационных сил, действующих на материю и излучение. Они определяются величиной в правой части уравнения, которая отражает суммарную плотность всех видов энергии и материи во Вселенной.

Эйнштейн понял, что добавление небольшого дополнительного постоянного члена в левую часть уравнения будет представлять небольшую дополнительную постоянную силу отталкивания повсюду в пространстве в дополнение к стандартному гравитационному притяжению между удаленными объектами, которое падает по мере увеличения расстояния между ними. Если она достаточно мала, эта дополнительная сила может быть незаметна в человеческих масштабах или даже в масштабах нашей Солнечной системы, где закон тяготения Ньютона соблюдается столь красиво. Но он подумал, что, поскольку она была постоянна повсюду в пространстве, она может возрастать в масштабах нашей галактики и быть достаточно большой, чтобы противодействовать силе притяжения между очень удаленными объектами. Таким образом, рассудил он, в больших масштабах это может привести к статичной Вселенной.

Эйнштейн назвал этот дополнительный член космологическим членом. Однако поскольку он был просто постоянным дополнением к уравнениям, то сейчас его обычно называют космологической постоянной.

После того, как он узнал, что Вселенная на самом деле расширяется, Эйнштейн обходился без этого члена и, как говорят, назвал решение добавить его в свои уравнения своей самой большой ошибкой.

Но избавиться от него не так просто. Это все равно что пытаться затолкать зубную пасту обратно в тюбик после того как вы ее выдавили. Все дело в том, что сейчас у нас совершенно иное представление о космологической постоянной, так что, если бы Эйнштейн не добавил этот член, то за прошедшие годы кто-то должен был бы это сделать.

Перемещение постоянной Эйнштейна из левой части его уравнений в правую — маленький шаг для математика, но гигантский скачок для физика. Хотя математически это сделать пустяк, как только этот член оказывается справа, где находятся все члены, вносящие вклад в энергию Вселенной, он представляет нечто совершенно отличное с физической точки зрения, а именно новый вклад в суммарную энергию. Но какого рода материю может отражать такой член?

Ответ — ничто.

Под ничем я подразумеваю не ничего, а совершенно ничего — в данном случае ничем мы обычно называем пустое пространство. Иначе говоря, если я возьму область пространства и избавлюсь от всего — пыли, газа, людей и даже проходящего через него излучения, то есть абсолютно от всего, что есть в этой области — если остальные пустое пространство будет что-то весить, то это будет означать существование космологического члена, такого, как выдумал Эйнштейн.

Итак, это заставляет космологическую постоянную Эйнштейна казаться еще безумнее! Любой четвероклассник скажет вам, сколько энергии содержит ничто, даже если он не знает, что такое энергия. Ответ должен быть нисколько.

Увы, большинство четвероклассников не учили квантовую механику, а также не изучали теорию относительности. Ибо, если учесть результаты специальной теории относительности Эйнштейна в квантовом пространстве, пустое пространство становится гораздо более странным, чем это было раньше. Фактически настолько странным, что даже физики, впервые обнаружившие и проанализировавшие это новое свойство, были почти готовы поверить, что оно на самом деле существует в реальном мире.

Первым человеком, успешно объединившим относительность и квантовую механику, был блестящий, немногословный британский физик-теоретик Поль Дирак, который ранее сам сыграл ведущую роль в развитии квантовой механики как теории.

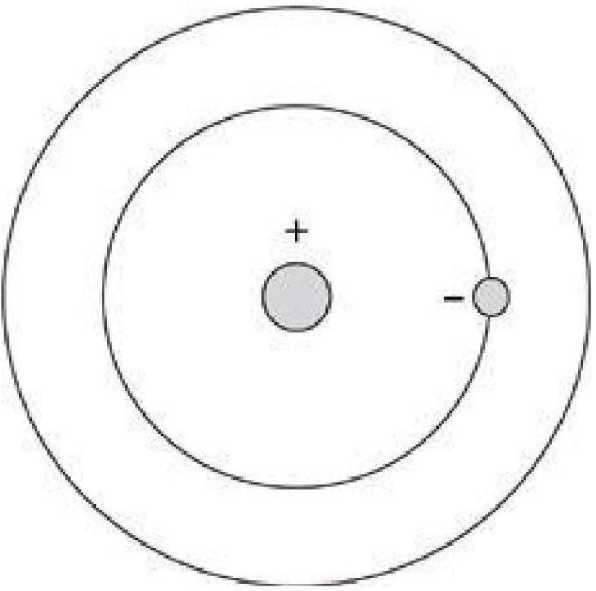
Квантовая механика была разработана в период с 1912 по 1927 год, в первую очередь благодаря работам гениального и знаменитого датского физика Нильса Бора, блестящего, молодого, энергичного австрийского физика Эрвина Шредингера и немецкого физика Вернера Гейзенберга. Квантовый мир, впервые предложенный Бором и математически уточненный Шредингером и Гейзенбергом, бросает вызов всем здравомыслящим представлениям, основанным на нашем знании объектов в человеческих масштабах. Бор первым предположил, что электроны в атомах вращаются вокруг центрального ядра, как планеты вокруг Солнца, но показал, что наблюдаемые правила атомных спектров (частот света, испускаемого различными элементами) можно понять, только если электроны каким-то образом ограничены наличием стабильных орбит с фиксированным рядом «квантовых уровней» и не могут свободно постепенно приближаться к ядру. Они могут двигаться между уровнями, поглощая или испуская только дискретные частоты, или кванты, света — те самые кванты, которые в 1905 году Макс Планк впервые предложил для понимания формы излучения горячих предметов.

Однако «правила квантования» Бора были довольно узкоспециализированы. В 1920-х Шредингер и Гейзенберг независимо показали, что эти правила можно было получить из основных принципов, если электроны подчинялись правилам динамики, которые отличались от тех, что применяются для макроскопических объектов, таких как бейсбольные мячи. Электроны могут вести себя и как волны, и как частицы, как бы распространяясь в пространстве (отсюда «волновая функция» Шредингера для электронов), и было показано, что измерения свойств электронов дают лишь вероятностные результаты, с различными комбинациями разных свойств, которые не могут быть точно измерены в одно и то же время (отсюда «принцип неопределенности» Гейзенберга).

Дирак показал, что математика, предлагаемая Гейзенбергом для описания квантовых систем (за которую Гейзенберг получил в 1932 году Нобелевскую премию), может быть получена по точной аналогии с известными законами, управляющими динамикой классических макроскопических объектов. Кроме того, позже ему также удалось продемонстрировать, что математическую «волновую механику» Шредингера также можно получить похожим образом, и она была формально эквивалентна формулировке Гейзенберга. Но Дирак также знал, что замечательная квантовая механика Бора, Гейзенберга и Шредингера применима только к системам, где были уместны законы Ньютона (а не теория относительности Эйнштейна), законы, управляющие классическими системами, по аналогии с которыми были построены квантовые системы.

Дирак любил мыслить на языке математики, а не картинных образов, и когда он сосредоточился на попытках заставить квантовую механику согласоваться с законами относительности Эйнштейна, он начал работать с различными уравнениями. К ним относятся сложные многокомпонентные математические системы, которые были необходимы, чтобы учесть тот факт, что электроны имеют «спин», иначе говоря, что они вращаются, как маленькие волчки, и имеют угловой момент, и что они также могут вращаться как по часовой стрелке, так и против часовой стрелки вокруг любой из осей.

В 1929 году он добился успеха. Уравнение Шредингера было красивым и точно описывало поведение электронов, движущихся со скоростью гораздо более медленной, чем свет. Дирак обнаружил, что если он превращал уравнение Шредингера в более сложное уравнение с помощью объектов, называемых матрицами — что на самом деле означало, что его уравнение в действительности описывало набор из четырех различных взаимосвязанных уравнений — он мог непротиворечиво объединить квантовую механику с относительностью, и, таким образом, в принципе, описать поведение системы, где электроны двигались на гораздо более высоких скоростях.

Однако была одна проблема. Дирак записал уравнение, предназначенное для описания поведения электронов, когда они взаимодействовали с электрическими и магнитными полями. Но для его уравнения, похоже, требовались также новые частицы, почти такие же, как электроны, но с противоположным электрическим зарядом.

В то время в природе была известна только одна элементарная частица с зарядом, противоположным электрону — протон. Но протоны не совсем похожи на электроны. Начнем с того, что они в 2000 раз тяжелее!

Дирак пришел в замешательство. В отчаянии он утверждал, что новые частицы были фактически протонами, но что каким-то образом при перемещении в пространстве взаимодействие протонов заставляло их действовать так, как будто они были тяжелее. Другим ученым, в том числе Гейзенбергу, не потребовалось много времени, чтобы показать, что это предположение не имело смысла.

Природа быстро пришла на помощь. В течение двух лет Дирак предлагал свое уравнение, а через год после того, как он капитулировал и признал, что, если его работа была верна, то должна существовать новая частица, экспериментаторы, наблюдая космические лучи, бомбардирующие Землю, обнаружили свидетельства новых частиц, идентичных электронам, но с противоположным электрическим зарядом, которых окрестили позитронами.

Дирак был оправдан, но он также признал свою прежнюю неуверенность в собственной теории, позже сказав, что его уравнение было умнее, чем он сам!

Мы теперь называем позитрон «античастицей» электрона, потому что оказалось, что открытие Дирака проявлялось повсеместно. Та же физика, что нуждается в античастице для существования электрона, нуждается в таких же частицах для существования почти всех элементарных частиц в природе. У протонов, например, есть антипротоны. Даже некоторые нейтральные частицы, такие как нейтроны, имеют античастицы. Когда частицы встречаются с античастицами, они аннигилируют в чистое излучение.

Хотя все это может звучать как научная фантастика (и антиматерия, несомненно, играет важную роль в «Звездном пути»), мы создаем античастицы все время в наших больших ускорителях частиц по всему миру. Поскольку античастицы в остальном имеют те же свойства, что и частицы, мир, сделанный из антиматерии, будет вести себя так же, как мир из материи, с антивлюбленными, сидящими в антимашинах и занимающимися любовью под анти-Луной. И это простая случайность в нашей жизни, которая, как нам кажется, вызвана гораздо более глубокими факторами, до которых мы дойдем позже, что мы живем во вселенной, которая состоит из материи, а не антиматерии, или во вселенной с равным количеством того и другого. Я хочу сказать, что в то время как антиматерия может показаться странной, она странная в том смысле, что и странные бельгийцы. На самом деле, они не странные, просто мы их редко встречаем.

Существование античастиц делает наблюдаемый мир гораздо более интересным местом, но это также делает пустое пространство гораздо более сложным.

Легендарный физик Ричард Фейнман был первым человеком, который привел нас к интуитивному пониманию того, почему теория относительности предполагает существование античастиц, и который также графически продемонстрировал, что пустое пространство не совсем пусто.

Фейнман понял, что теория относительности говорит нам, что наблюдатели, движущиеся с разной скоростью, будут по-разному измерять такие величины, как расстояние и время. Например, будет казаться, что время замедляется для объектов, движущихся очень быстро. Если каким-то образом объекты могли бы путешествовать быстрее света, они бы, казалось, двигались бы назад во времени, что является одной из причин, по которой скорость света обычно считают пределом космической скорости.

Ключевым принципом квантовой механики, однако, является принцип неопределенности Гейзенберга, который, как я уже упоминал, утверждает, что для некоторых пар величин, таких как местоположение и скорость, невозможно одновременно определить их точные значения для данной системы. С другой стороны, если вы измеряете данную систему только в фиксированный, конечный промежуток времени, вы не можете точно определить его полную энергию.

Все это означает, что, для очень короткого времени, настолько короткого, что вы не можете измерить скорость частиц с высокой точностью, квантовая механика допускает возможность, что эти частицы ведут себя так, как если бы они двигались быстрее света! Но, если они движутся быстрее света, Эйнштейн говорит нам, что они должны вести себя так, как будто они движутся назад во времени!

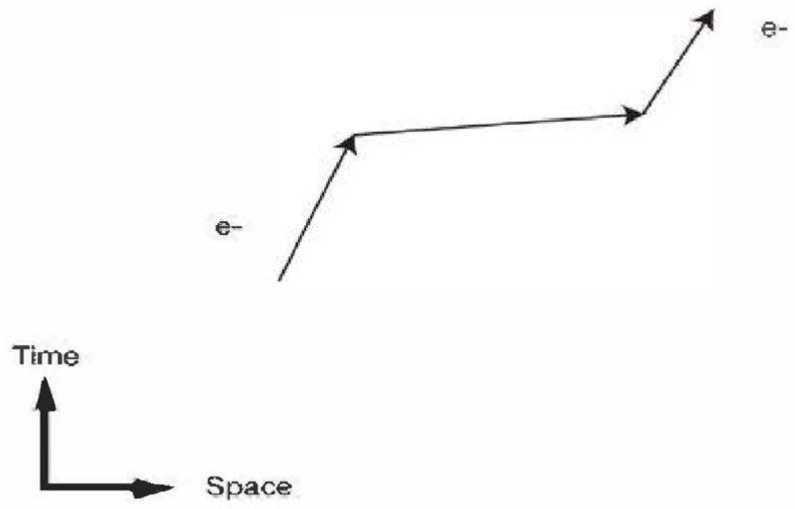
Фейнман был достаточно храбр, чтобы воспользоваться этой, казалось бы, сумасшедший возможностью серьезно и изучить ее последствия. Он нарисовал следующую схему электрона, движущегося с места на место, периодически ускоряющегося в середине своего путешествия до скорости, большей, чем скорость света.

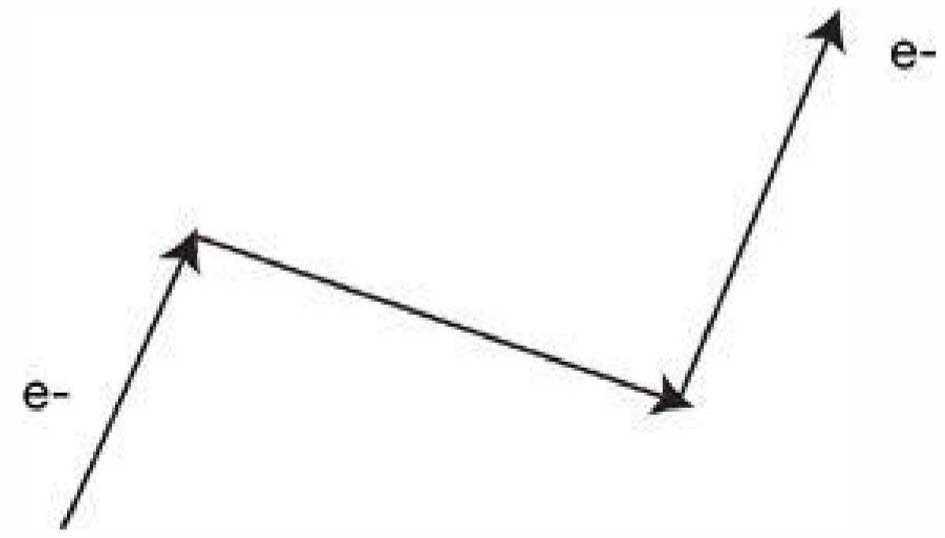
Он понял, что теория относительности говорит нам, что другой наблюдатель мог бы альтернативно измерить то, что выглядело бы как показано ниже, при этом электрон будет двигаться то вперед, то назад во времени, а затем снова вперед.

Однако отрицательный заряд, движущийся назад во времени, математически эквивалентен положительному заряду, движущемуся вперед во времени! Таким образом, относительность потребовала бы наличия положительно заряженных частиц с такой же массой и другими свойствами, как у электронов.

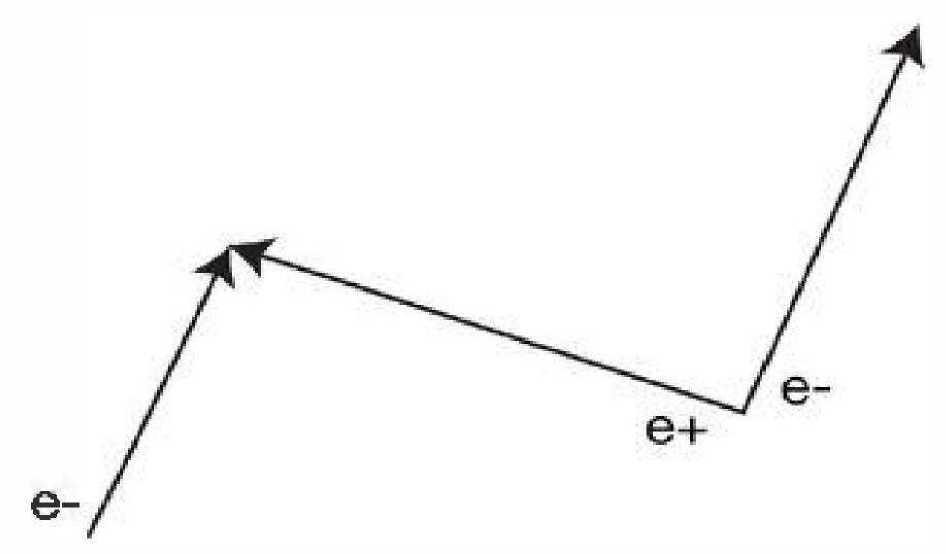
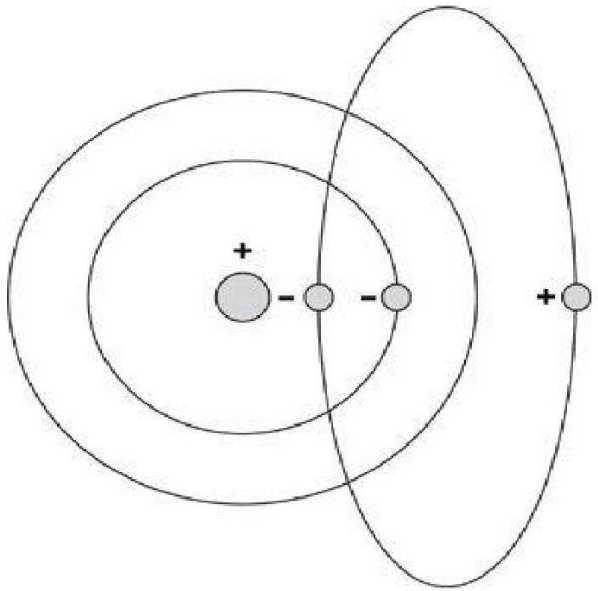
В этом случае второй рисунок Фейнмана можно интерпретировать следующим образом: движется один электрон, потом в другой точке пространства из ничего создается пара позитрон-электрон, а затем позитрон встречает первый электрон, и оба аннигилируют. Впоследствии остается один движущийся электрон.

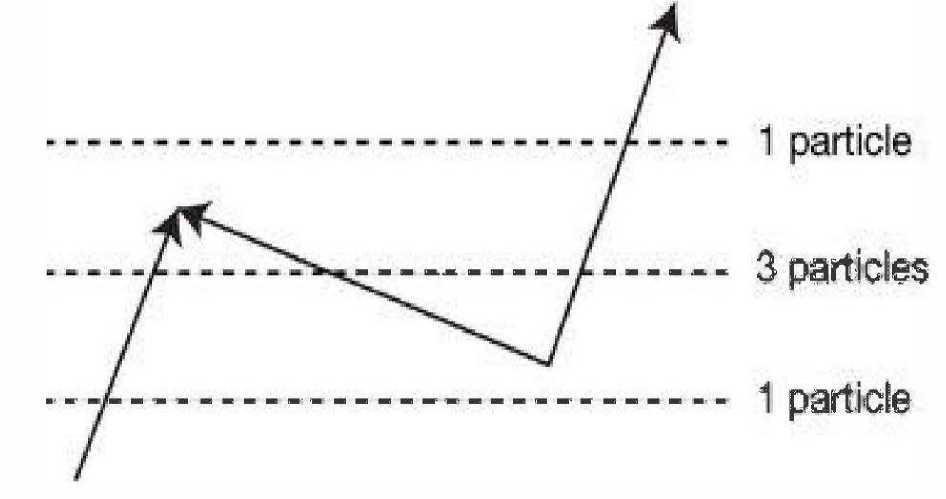
Если вас это не смущает, то необходимо учитывать следующее: на некоторое время, даже если у вас вначале только одна частица, и одна частица в конце, в течение короткого времени есть три движущихся частицы:

В краткий момент посредине, по крайней мере на некоторое время, что-то рождается из ничего! Фейнман красиво описывает этот очевидный парадокс в своей работе «Теория позитронов» (1949 г.), используя восхитительную военную аналогию:

Поскольку период времени в течение этой «петли» настолько короткий, что мы не можем прямо измерить все частицы, квантовая механика и теория относительности предполагают, что эта странная ситуация не просто допускается, она возникает обязательно. Частицы, которые появляются и исчезают в масштабах времени, слишком коротких для измерения, называют виртуальными частицами.

Теперь открытие целого ряда новых частиц в пустом пространстве, которых нельзя измерить, очень похоже на множество ангелов, сидящих на булавочной головке. И это была бы примерно такая же бесплодная идея, если бы у этих частиц не было никаких других заметных эффектов. Тем не менее, хотя их нельзя наблюдать непосредственно, оказывается, их косвенные эффекты производят большую часть свойств Вселенной, которые мы знаем сегодня. Мало того, можно рассчитать влияние этих частиц точнее, чем при любом другом научном расчете.

Рассмотрим, например, атом водорода — систему, которую Бор попытался объяснить, разработав свою квантовую теорию, а Шредингер позже попытался описать, выведя свое знаменитое уравнение. Красота квантовой механики была в том, что она могла объяснить определенные цвета света, излучаемого водородом, когда он нагрет, утверждая, что электроны, вращающиеся вокруг протона, могут существовать только на дискретных уровнях энергии, и когда они прыгают между уровнями, они поглощают или излучают только фиксированный набор частот света. Уравнение Шредингера позволяет вычислить предсказанные частоты, и оно дает почти абсолютно правильный ответ.

Но не совсем.

Когда спектр водорода изучили более тщательно, то увидели, что он был более сложным, чем оценивалось ранее, с некоторыми дополнительными неболь-тттими разделениями между наблюдаемыми уровнями, называемыми «тонкой структурой» спектра. Хотя эти разделения были известны со времен Бора, и было подозрение, что, возможно, релятивистские эффекты имеют к ним какое-то отношение, пока релятивистская теория не стала полностью доступна, никто не мог подтвердить это подозрение. К счастью, благодаря уравнению Дирака удалось улучшить предсказания по сравнению с уравнением Шредингера и воспроизвести общую структуру наблюдений, в том числе тонкую структуру.

Пока все хорошо, но в апреле 1947 года экспериментатор из Соединенных Штатов Уиллис Лэмб и его ученик Роберт С. Резерфорд провели эксперимент, который мог бы показаться невероятно плохо мотивированным. Они поняли, что имели техническую возможность измерять структуру уровней энергии атомов водорода с точностью до 1 части на 100 миллионов.

Зачем им это было надо? Что ж, всякий раз, когда экспериментаторы находят новый метод измерения чего-то со значительно большей точностью, чем это было возможно раньше, это часто бывает достаточной мотивацией для них, чтобы идти вперед. При этом часто обнаруживаются целые новые миры, как тогда, когда голландский ученый Антони ван Левенгук первым посмотрел на каплю, казалось бы, чистой воды с помощью микроскопа в 1676 году и обнаружил, что она кипит жизнью. В данном случае, однако, у экспериментаторов была более прямая мотивация. До эксперимента Лэмба доступная экспериментальная точность не позволяла детально проверить предсказание Дирака.

Уравнение Дирака предсказывало общую структуру новых наблюдений, но ключевым вопросом, на который хотел ответить Лэмб, было предсказывало ли оно их детально. Это был единственный способ действительно проверить теорию. И когда Лэмб проверил эту теорию, казалось, он получил неправильный ответ, в масштабе примерно 100 частей на миллиард, что значительно выше чувствительности его аппарата.

Такое маленькое расхождение с экспериментом может показаться незначительным, но предсказания теории Дирака в ее простейшей интерпретации были однозначны, как и эксперимент, и они отличались.

В течение следующих нескольких лет за дело взялись лучшие теоретические умы в физике и попытались разрешить это несоответствие. Ответ был получен после огромной работы, и когда пыль осела, стало ясно, что уравнение Дирака на самом деле дает совершенно правильный ответ, но только если учитывать влияние виртуальных частиц. Графически это можно представить следующим образом. Атомы водорода, как правило, в книгах по химии изображаются вот так, с протоном в центре и электроном, вращающимся вокруг него, прыгающим между различными уровнями:

Однако как только мы допускаем возможность, что электронно-позитронные пары могут ненадолго спонтанно появляться из ничего, прежде чем снова уничтожить друг друга, в течение любого короткого времени атом водорода в действительности выглядит следующим образом:

В правой части рисунка я нарисовал такую пару, которая затем аннигилировала в верхней части. Виртуальный электрон, будучи заряженным отрицательно, любит держаться неподалеку от протона, а позитрон любит оставаться дальше. В любом случае, из этого рисунка видно, что фактическое распределение заряда в атоме водорода не объясняется, в любой момент, только одним электроном и протоном.

Примечательно, что мы, физики, усвоили (после всей этой тяжелой работы Фейнмана и других), что мы можем использовать уравнение Дирака для вычисления, с произвольно высокой точностью, воздействия на спектр водорода всех возможных виртуальных частиц, которые могут существовать периодически поблизости от него. И когда мы это сделали, мы выдали самый лучший, самый точный прогноз во всей науке. Все другие научные прогнозы бледнеют в сравнении с ним. В астрономии самые последние наблюдения космического микроволнового фонового излучения позволяют сравнить их с теоретическими предсказаниями на уровне, возможно, 1 часть на 100 000, что замечательно. Тем не менее, с помощью уравнения Дирака и предсказанного существования виртуальных частиц мы можем вычислить значение атомных параметров и сравнить их с результатами наблюдений, и они замечательно согласуются на уровне примерно 1 часть на миллиард или лучше!

Поэтому виртуальные частицы существуют. Тогда как с захватывающей точностью, доступной в атомной физике, вряд ли что-то может сравниться, есть одно место, где виртуальные частицы играют ключевую роль, которое фактически может иметь более непосредственное отношение к центральному вопросу этой книги. Оказывается, они ответственны за большую часть вашей массы, и массы всего, что мы видим во Вселенной.

Один из крупных успехов в 1970-е годы в нашем фундаментальном понимании материи пришел с открытием теории, точно описывающей взаимодействие кварков, частиц, составляющих протоны и нейтроны, формирующих основную часть вещества, из которого сделаны вы и всё, что вы можете видеть. Математика, связанная с этой теорией, сложна, и потребовалось несколько десятилетий, прежде чем были разработаны методы, способные с нею справиться, особенно в режиме, где сильное взаимодействие между кварками стало ощутимым. Были приложены неимоверные усилия, в том числе построены несколько самых сложных компьютеров параллельной обработки, одновременно использующих десятки тысяч отдельных процессоров, с тем, чтобы попытаться вычислить фундаментальные свойства протонов и нейтронов, частиц, которые мы фактически измеряем.

После всей этой работы у нас теперь есть хорошее представление о том, как на самом деле выглядят внутренности протона. В нем может содержаться три кварка, но есть также многое другое. В частности, виртуальные частицы, отображающие частицы и поля, передающие сильное взаимодействие между кварками, постоянно то возникают, то исчезают. Вот снимок, как всё выглядит на самом деле. Конечно, это не настоящая фотография, а, скорее, художественная визуализация математики, регулирующей динамику кварков и полей, которые их связывают. Необычные формы и разные оттенки отражают силу полей, взаимодействующих друг с другом и с кварками внутри протона, когда виртуальные частицы спонтанно то возникают, то исчезают.

Протон периодически наполняется такими виртуальными частицами и фактически, когда мы пытаемся оценить, какой вклад они могли бы вносить в массу протона, мы находим, что сами кварки обеспечивают очень малую часть от общей массы, и что поля, создаваемые этими частицами, вносят большую часть энергии, составляющей энергию покоя протона и, следовательно, его массу покоя. То же самое верно для нейтрона, и, так как вы состоите из протонов и нейтронов, то же самое верно для вас!

Итак, если мы можем рассчитать воздействие виртуальных частиц на пустое пространство внутри и вокруг атомов, и мы можем рассчитать воздействие виртуальных частиц на пустое пространство внутри протонов, можем ли мы рассчитать воздействие виртуальных частиц на само пустое пространство?

Что ж, этот расчет вообще-то сделать труднее. Причина в том, что, когда мы рассчитываем воздействие виртуальных частиц на атомы или на массу протона, мы на самом деле рассчитываем полную энергию атома или протона, включая виртуальные частицы, а затем вычисляем полную энергию, которую внесли бы виртуальные частицы без атома или протона (т. е. в пустом пространстве), а затем вычитаем эти два числа, чтобы найти чистое воздействие на атом или протон. Мы так делаем, потому что когда мы пытаемся решить соответствующие уравнения, оказывается, что каждая из этих двух энергий формально бесконечна, но когда мы вычитаем эти две величины, у нас остается конечная разность, причем такая, которая в точности совпадает с измеренным значением!

Однако если мы хотим вычислить воздействие виртуальных частиц на одно только пустое пространство, у нас не из чего вычитать, и в ответе мы получим, следовательно, бесконечность.

Однако бесконечность — не самое приятное число, по крайней мере, для физиков, и мы стараемся избегать его, когда это возможно. Очевидно, что энергия пустого пространства (или чего-нибудь другого, если на то пошло) не может быть физически бесконечной, так что мы должны найти способ сделать расчет и получить конечный ответ.

Причину бесконечности легко объяснить. Когда мы рассматриваем все возможные виртуальные частицы, которые могут появиться, из принципа неопределенности Гейзенберга (который, я напомню, говорит, что неопределенность измеряемой энергии системы обратно пропорциональна промежутку времени, за который вы ее наблюдаете) следует, что частицы, несущие больше всего энергии, могут появиться спонтанно из ничего, если только они затем исчезают в кратчайшее время. Поэтому, в принципе, частицы могут обладать почти бесконечной энергией при условии, что они исчезают в почти бесконечно малое время.

Тем не менее, законы физики, как мы их понимаем, применимы только для времени и расстояний больших, чем определенное значение, соответствующее масштабам, где необходимо учитывать эффекты квантовой механики при попытке понять гравитацию (и связанные с ней воздействия на пространство-время). Пока у нас нет теории «квантовой гравитации», как ее называют, мы не можем доверять экстраполяциям, которые выходят за эти пределы.

Таким образом, мы могли бы надеяться, что новая физика, связанная с квантовой гравитацией, каким-то образом отсечет эффекты виртуальных частиц, которые живут меньше, чем «планковское время», как его называют. Если мы затем рассмотрим суммарное действие только виртуальных частиц с энергией, равной или ниже энергии, которую позволяет это временное ограничение, мы приходим к конечной оценке энергии, вносимой в ничто виртуальными частицами.

Но есть проблема. Это число оказывается примерно в

раз больше, чем энергия, связанная со всей известной материей во Вселенной, в том числе с темной материей!

Если расчет расположения атомных энергетических уровней, включая виртуальные частицы, является лучшим вычислением во всей физике, то эта оценка энергетического пространства — на 120 порядков большая, чем энергия всего остального во Вселенной — это, несомненно, худшее вычисление! Если энергия пустого пространства как-то приближается к этому огромному числу, возникающая сила отталкивания (помните, энергия пустого пространства равна космологической постоянной) была бы достаточно большой, чтобы взорвать Землю сегодня, но что более важно, она была бы так велика в древние времена, что все, что мы сейчас видим в нашей Вселенной, оттолкнулось бы друг от друга так быстро в первые доли секунды после Большого Взрыва, что ни одна структура, ни звезды, ни планеты и ни люди никогда бы не образовались.

Эту проблему, подходяще названную проблемой космологической постоянной, существовавшую задолго до того, как я стал аспирантом, впервые совершенно ясно выразил русский космолог Яков Зельдович примерно в 1967 году. Она остается нерешенной и, пожалуй, самой глубокой нерешенной фундаментальной проблемой в физике сегодня.

Несмотря на то, что мы не имели ни малейшего представления, как решить эту проблему в течение более чем сорока лет, мы, физики-теоретики, знали, что ответ должен был быть. Как четвероклассник, который, я полагаю, догадался бы, что энергия пустого пространства равна нулю, мы тоже чувствовали, что, когда конечная теория будет получена, она объяснит, как аннулируются эффекты виртуальных частиц, оставляя пустое пространство с ровно нулевой энергией. Или ничто. Или, скорее, Ничто.

Наши рассуждения были лучше, чем рассуждения четвероклассника, или мы так думали. Нам нужно было уменьшить величину энергии пустого пространства от действительно гигантского значения, предложенного наивной оценкой, до величины, соответствующей верхним пределам, допустимым наблюдением. Это потребовало бы какого-то способа вычесть из очень большого положительного числа другое очень большое положительное число, так, чтобы сократить 120 знаков, оставляя что-то ненулевое под 121 знаком! Но нет ни одного прецедента в науке для сокращения двух больших чисел с такой точностью, чтобы осталось только что-то мизерное.

Однако ноль — это число, которое легко получить. Примеры симметрии в природе часто позволяют продемонстрировать, что есть абсолютно равные и противоположные вклады, получаемые в разных местах в расчете, которые полностью сокращаются, совершенно ничего не оставляя в остатке. Или, снова же, Ничего.

Таким образом, мы, теоретики, могли расслабиться и спать спокойно. Мы не знали, как добиться окончательного ответа, но мы были уверены, что он должен был быть.

У природы, однако, было на уме что-то другое.