Большая часть принимаемых нами в жизни важных решений связана с вероятностями. Хотя более всестороннее обсуждение принятия решений будет проводиться в главе 8, давайте рассмотрим применение древовидных диаграмм в процессе принятия решений.

Эдит пытается выбрать для себя специализацию в колледже. Она учится в университете, где для специализации по каждому из предметов надо сдавать отдельные вступительные экзамены. Она серьезно думает о том, чтобы стать бухгалтером. Она знает, что на отделение бухгалтерии принимают только 25 % из желающих туда поступить. Семьдесят процентов поступивших оканчивают курс, и 90 % окончивших успешно сдают государственные экзамены на звание бухгалтера и становятся бухгалтерами. Эдит хотела бы узнать, каковы ее шансы стать бухгалтером, если она выберет эту специализацию.

Чтобы ответить на ее вопрос, нарисуем древовидную диаграмму, ветви которой будут указывать «путь» к успешному овладению профессией бухгалтера.

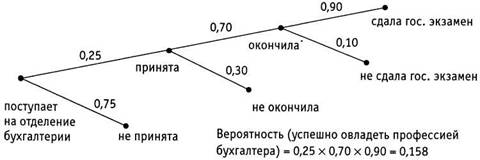
Из приведенной выше диаграммы вы видите, что вероятность успешно овладеть профессией бухгалтера равна 0,25 х 0,70 х 0,90, т. е. 0,158. Получив такой результат, Эдит должна обдумать другие варианты. Например, она может попробовать поступать сразу на отделения бухгалтерии и педагогики. Она может снова подсчитать свои шансы на успех по одной из этих профессий, по обеим сразу (если такой вариант для нее возможен) или вероятность неудачи и там, и там.

В этом примере предполагается, что у нас нет никакой дополнительной информации, на основе которой можно оценивать шансы Эдит на успех. Предположим теперь, что нам известно, что у Эдит прекрасные способности к математике. Приведет ли наличие такого рода информации к изменению соответствующих вероятностей? Повысится ли вероятность того, что Эдит будет принята, окончит курс и успешно овладеет профессией, требующей знания математики? Интуитивно хочется ответить «да». Давайте на следующем примере рассмотрим, как изменится задача вычисления вероятности успеха, если учитывать дополнительную информацию.