Силлогистическое рассуждение

Ничто, доступное для понимания, меня не удивляет. Меня приводит в недоумение логика.

Льюис Кэрролл (1832–1898)

Силлогистическое рассуждение — это вид рассуждения, где требуется определить, следует ли из двух или нескольких утверждений данное заключение. Одним из видов силлогизмов является категорический силлогизм. Категорический силлогизм включает в себя кванторные слова, или термины, указывающие на количество. Кванторными словами являются такие термины, как «все», «некоторые» и «ни один». Они показывают, сколько элементов принадлежит к определенной категории.

Обычно силлогизм состоит из двух утверждений, которые называются посылками, и третьего утверждения, которое называется заключением. В категорических силлогизмах в посылках и заключении присутствуют кванторные слова. Задача заключается в том, чтобы определить, является ли заключение логическим следствием посылок.

Посылки и заключение силлогизма классифицируются по наклонениям (moods). Существует четыре вида наклонений, или сочетаний положительных и отрицательных утверждений с терминами «все» и «некоторые». Эти четыре вида наклонений приводятся ниже.

Как мы видим, суждение является общим, если оно содержит термины «все» или «ни один», частным — если содержит термин «некоторые», отрицательным — если содержит «не», и утвердительным, если оно не является отрицательным. Таким образом, вид суждения определить довольно легко, если найти в нем ключевые термины.

Ниже приведено несколько силлогизмов. Каждый из них состоит из двух посылок и заключения. Подумайте над каждым из них и определите, валидным (В) или нет (Н) является заключение. Чтобы заключение было валидным, оно должно всегда быть правильным при условии правильности посылок. Другими словами, утверждая об истинности силлогизма, вы как бы говорите: «Если посылки истинны, то заключение должно быть истинным». Можно выразиться и так: «Следует ли заключение из посылок?» Если вы можете найти хотя бы один случай, когда при истинных посылках заключение будет ложным, то оно не является валидным. Не продолжайте чтение, пока вы не завершите работу над следующими силлогизмами.

1. Посылка 1. Все люди, получающие социальные пособия, бедны.

Посылка 2. Некоторые бедные люди являются нечестными

Заключение. Некоторые люди, получающие социальные пособия, являются нечестными. В или Н?

2. Посылка 1. Никто из родителей не понимает детей.

Посылка 2. Некоторые учителя понимают детей.

Заключение. Никто из родителей не является учителем. В или Н?

3. Посылка 1. Некоторые юристы не умны

Посылка 2. Некоторые умные люди богаты

Заключение. Некоторые юристы богаты В или Н?

4. Посылка 1. Все физики хорошо разбираются в математике.

Посылка 2. Некоторые студенты являются физиками.

Заключение. Некоторые студенты хорошо разбираются в математике. В или Н?

5. Посылка 1. Всем американцам необходима медицинская страховка.

Посылка 2. Все, кому необходима медицинская страховка, должны голосовать за нее.

Заключение. Все американцы должны голосовать за медицинскую страховку. В или Н?

С точки зрения законов логики не имеет значения, как сформулирован силлогизм — в абстрактной форме с использованием буквенных обозначений Aw В (например, некоторые А не есть В), с использованием бессмысленных слов, таких как куздра и бокр (Все куздры являются бокрами) или с помощью осмысленных понятий, таких как юристы и прикольный (Ни один юрист не является прикольным). Логические правила, по которым мы определяем, следует ли заключение из данных посылок, остаются одними и теми же. Фактически мы говорим: «Все __ являются __». Совершенно не важно, что мы вставим на пропущенные места — буквы,

бессмысленные или осмысленные слова или даже картинки; с любыми объектами следует обращаться одинаково. Тем не менее с точки зрения психологии существуют важные различия, связанные с содержанием. Один из способов избежать воздействия наших предубеждений на процессы мышления с использованием кванторных слов — это использование круговых диаграмм, которые, так же как линейные и древовидные диаграммы, снижают нагрузку на кратковременную память и делают отношения очевидными и наглядными.

С точки зрения законов логики не имеет значения, как сформулирован силлогизм — в абстрактной форме с использованием буквенных обозначений А и В (например, некоторые А не есть В), с использованием бессмысленных слов, таких как куздра и бокр (Все куздры являются бокрами) или с помощью осмысленных понятий, таких как юристы и прикольный (Ни один юрист не является прикольным). Логические правила, по которым мы определяем, следует ли заключение из данных посылок, остаются одними и теми же. Фактически мы говорим: «Все __ являются __». Совершенно не важно, что мы вставим на пропущенные места — буквы, бессмысленные или осмысленные слова или даже картинки; с любыми объектами следует обращаться одинаково. Тем не менее с точки зрения психологии существуют важные различия, связанные с содержанием. Один из способов избежать воздействия наших предубеждений на процессы мышления с использованием кванторных слов — это использование круговых диаграмм, которые, так же как линейные и древовидные диаграммы, снижают нагрузку на кратковременную память и делают отношения очевидными и наглядными.

Проверка валидности заключения

Как вы проверяли валидность заключений в предложенных силлогизмах? Для того чтобы определить, следует ли заключение силлогизма из его посылок, существуют методы двух различных типов. Если вы читаете главы этой книги по порядку, то знаете, что общий подход к совершенствованию навыков мышления подразумевает целенаправленное использование как пространственных, так и вербальных методов. Эти же два подхода применимы и в данном случае. Сначала я представлю пространственный метод проверки заключений, а затем предложу несколько вербальных правил, которые также можно использовать. Оба метода «срабатывают», но возможно, что вы отдадите предпочтение одному из них. Я в течение многих лет преподавала этот материал студентам колледжа и обнаружила, что многие студенты явно предпочитают либо круговые диаграммы, либо вербальные правила.

Круговые диаграммы для проверки валидности рассуждений

Один из способов проверки истинности заключения основан на использовании круговых диаграмм, которые отражают связи между тремя терминами (А, В, С или любыми элементами, которые мы вставим на пропущенные места). Степень наложения кругов друг на друга отражает отношения включения или исключения между классами понятий.

Существует несколько различных методов рисования диаграмм для изображения связей между терминами силлогизма. Один из этих методов назван в честь английского математика и логика Венна, который жил в XIX в. и первым предложил использовать подобные диаграммы. Диаграммы Венна — это те же самые диаграммы, которые вы, возможно, рисовали на уроках математики, если изучали теорию множеств. (Этот способ обучения «новой математике» пользовался большой популярностью, но потом был заброшен, и педагоги вернулись к «старой математике».) Второй вариант диаграмм для отображения связей — это диаграммы Эйлера. Согласно популярной легенде, швейцарский математик Леонард Эйлер, живший в XVIII в., придумал этот метод, когда получил задание обучить немецкую принцессу искусству силлогистических рассуждений. Поскольку принцесса испытывала трудности при понимании задач, Эйлер изобрел простой метод, помогающий понять отношения между терминами и проверить правильность рассуждений. Третий метод заключается в изображении трех перекрывающих друг друга кругов. Во всех этих методах круги отражают принадлежность к какому-либо классу. Различия между данными методами для нас не имеют значения, и в целом такая методика проверки заключений носит название круговых диаграмм. Если вы уже изучали другой метод рисования круговых диаграмм (например, на уроках теории множеств или логики) и привыкли к нему, то продолжайте им пользоваться.

Внимательно рассмотрите рис. 4.4. В левом столбце перечислены четыре наклонения, которые могут иметь суждения силлогизма. Рядом с каждым изображена круговая диаграмма, которая правильно отражает связи между терминами силлогизма. Сделайте перерыв в чтении и как следует изучите рис. 4.4. Один из кругов изображает все, что является А, а другой — все, что является В. При проведении дедуктивных рассуждений не имеет значения, что именно представляют собой А и В. В примере, приведенном на рис. 4.4, А обозначает ангелов, а В — лысых, но эти буквы могли бы обозначать все что угодно. Я могла бы с таким же успехом обозначить буквой А студентов колледжей, а буквой В — панк-рокеров.

Посмотрите, как расположены круги, чтобы создать «картинку» того, что описано словами. Давайте начнем с середины таблицы, поскольку общее отрицание является самым простым примером. Когда мы говорим «Ни одно А не есть В», то это означает, что ни одно понятие, относящееся к классу А, не принадлежит также и к классу В. Такая связь между понятиями отражается путем изображения кругов с пометками А и В, которые не касаются друг друга и не перекрываются. Существует только один способ изображения этой связи. Заметьте, что когда мы говорим «Ни одно А не есть В», мы одновременно утверждаем, что «Ни одно В не есть Л». Видите ли вы это, рассматривая круговую диаграмму?

Рис. 4.4. Круговые диаграммы, правильно отражающие взаимосвязи между посылками в силлогизмах

Обратите внимание, что кванторное слово «все» может иметь две правильные интерпретации, кванторное слово «некоторые» — четыре правильные интерпретации, кванторное слово «ни один» имеет одну правильную интерпретацию, а кванторное слово «некоторые не» — три.

Рассмотрим теперь общее утверждение «Все А есть В». Вновь воспользуемся двумя кругами — один с пометкой Л, а другой с пометкой В. И опять нам нужно нарисовать круги таким образом, чтобы они отражали связь, при которой все, что относится к классу А, относится и классу В. Как видно из рис. 4.4, существуют два различных способа изображения такой связи, поскольку существует две возможные правильные трактовки смысла этой связи. Нарисовав круг А внутри круга В, мы отразим случай, когда «Все А есть В, но существуют некоторые В, не являющиеся А» (некоторые лысые не являются ангелами). На рисунке рядом показан случай, когда «Все А есть В, и все В есть А» (все лысые являются ангелами). Когда нам говорят, что «Все А есть В», может быть верна любая из этих интерпретаций.

Если вам показалось, что это трудно, не падайте духом. Скоро станет легче, по мере того как вы поработаете над примерами и осмыслите материал. Рассмотрим оставшиеся две возможности, изображенные на рис. 4.4. Частное отрицание (Некоторые А не есть В) можно изобразить тремя способами, а частное утверждение (Некоторые А есть В) — четырьмя. Рассмотрим, как вообще могут быть расположены круги. Существует пять различных вариантов размещения двух кругов относительно друг друга, и каждый из них отражает свой смысл!

Давайте нарисуем круговые диаграммы, отражающие связи между терминами первого силлогизма. Первые две фразы являются посылками. Выпишите каждую из посылок и нарисуйте рядом с ней соответствующую круговую диаграмму. Например, в первой посылке утверждается, что «Все люди, получающие социальные пособия, бедны». В структурной форме она имеет вид «Все А есть В», где А обозначает «людей, получающих социальные пособия», а В — «бедных». Вы уже можете распознать тип этой посылки — общеутвердительный. Посмотрите на рис. 4.4, найдите строку с общеутвердительным наклонением и вы увидите, что существует два возможных способа расположения кругов, соответствующих этой посылке. Повторите эти же действия со второй посылкой: «Некоторые бедные люди являются нечестными». Вы уже решили, что А = «люди, получающие социальные пособия», а В = «бедные». Новый термин — «нечестные» — можно обозначить буквой С. Тогда вторая посылка принимает вид «Некоторые В есть С». Это пример частного утверждения. Посмотрите на строку рис. 4.4 с частноутвердительным наклонением и вы увидите, что существует четыре возможных способа расположения кругов, соответствующих этой связи. Единственное отличие заключается в том, что во второй посылке мы пользуемся для обозначения классов буквами В и С. Таким образом, круговые диаграммы первых двух посылок будут иметь следующий вид:

А = люди, получающие социальные пособия, В = бедные, С = нечестные.

1. Все люди, получающие социальные пособия, бедны (Все А есть В).

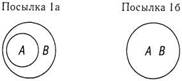
2. Некоторые бедные люди являются нечестными (Некоторые В есть С).

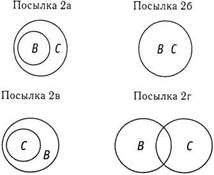
Чтобы проверить истинность заключения, мы будем систематически комбинировать каждую из фигур посылки 1 с каждой из фигур посылки 2. Если найдется хотя бы одно сочетание, которое не соответствует заключению, то можно остановиться и сделать вывод, что заключение не является валидным. Если мы переберем все возможные сочетания фигур посылок 1 и 2 и все они не будут противоречить заключению, то заключение является валидным. Другими словами, если все сочетания посылки 1 с посылкой 2 подтверждают заключение, то оно валидно. Первые несколько раз эта процедура может показаться вам трудоемкой, но вскоре вы будете «видеть» ответы и находить способы сокращения процесса проверки всех возможных сочетаний.

Вот заключение:

Некоторые люди, получающие социальные пособия, являются нечестными

(Некоторые А есть С.)

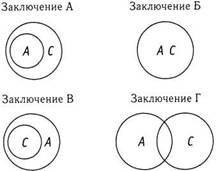
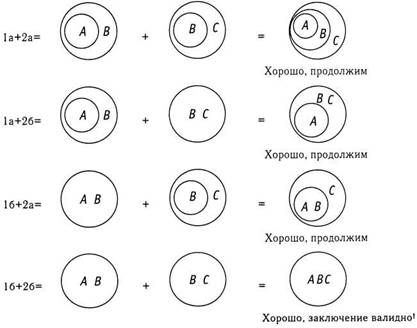
Посылку 1 можно изобразить двумя способами, а посылку 2 — четырьмя. Я обозначила два рисунка для посылки 1 номерами 1а и 1б, а четыре рисунка для посылки 2 — номерами 2а, 2б, 2в и 2 г. Чтобы работать систематично, вам необходимо использовать правила комбинаторного рассуждения, изложенные в предыдущем разделе. Начните с рисунка 1а и комбинируйте его по очереди с 2а, 2б, 2в и 2 г. Затем повторите эту же процедуру с рисунком 1б, проверяя его сочетания с 2а, 2б, 2в и наконец с 2 г. Конечно, есть надежда, что не придется проводить всю эту процедуру до конца, потому что можно остановиться, как только вы найдете первое сочетание, которое противоречит заключению о том, что «Некоторые А есть С». Давайте попробуем вместе.

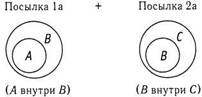
При сочетании этих двух изображений я получу рисунок, где А будет внутри В, а В внутри С:

Это сочетание соответствует заключению о том, что «Некоторые А есть С» (вариант А). Продолжим!

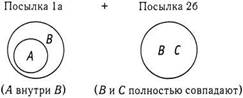
Сочетая 1 а с 26, я получаю рисунок, на котором А находится внутри круга, изображающего В и С:

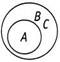
Это не противоречит заключению о том, что «Некоторые А есть С» (вариант А). Продолжим!

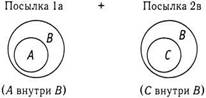
Здесь ситуация несколько более запутанная, поскольку существует несколько возможных способов сочетаний 1а с 2в, и нам необходимо проверять эти способы, пока мы не переберем все сочетания или не найдем хотя бы одно, противоречащее заключению. Давайте нарисуем все варианты взаимного расположения кругов, при котором А находится внутри В и С находится внутри В.

А и С — это один и тот же круг, находящийся внутри В.

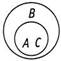
Этот результат по-прежнему не противоречит тому, что «Некоторые А есть С» (вариант Б). Продолжим!

Круги А и С находятся внутри В и частично накладываются друг на друга.

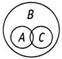
Этот результат по-прежнему не противоречит тому, что «Некоторые А есть С» (вариант Г). Продолжим!

Круги А и С — два отдельных круга, находящихся внутри В.

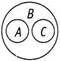
Этот результат не согласуется с заключением о том, что «Некоторые А есть С» (такого варианта рисунка для заключения у нас нет).

Можно остановиться! При данных двух посылках заключение «Некоторые люди, получающие социальные пособия, являются нечестными» нельзя считать валидным.

Я знаю, что проделанная работа кажется очень трудоемкой, но после того как вы решите несколько подобных задач, вы научитесь сразу находить комбинации, которые указывают на то, что заключение не валидно, поэтому не потребуется проверять все возможные комбинации. Но до тех пор, пока вы этому не научитесь, проверяйте систематически все комбинации. Перечень шагов, необходимых для проверки истинности заключения с помощью круговых диаграмм, приводится в табл. 4.2. Сделайте паузу и изучите эти шаги. При работе над остальными силлогизмами пользуйтесь этой таблицей.

Таблица 4.2. Последовательность проверки истинности заключения с помощью круговых диаграмм:

1. Выпишите каждую посылку и заключение силлогизма

2. Рядом с каждым утверждением изобразите все возможные правильные диаграммы, пользуясь рис. 4.1.

3. Систематически комбинируйте каждую из диаграмм посылки 1 со всеми диаграммами посылки 2. Начните с комбинации посылки 1а (первая диаграмма посылки 1) и посылки 2а (первая диаграмма посылки 2). Затем проверьте комбинации посылки 1а со всеми остальными диаграммами посылки 2, после чего переходите к посылке 1б, сочетая ее со всеми диаграммами посылки 2. Продолжайте действовать аналогичным образом (посылка 1в со всеми диаграммами посылки 2, затем посылка 1 г со всеми диаграммами посылки 2), до тех пор, пока…

4…не найдете хотя бы одно сочетание, которое не согласуется с заключением, или

5. …проверите все комбинации диаграмм посылок 1 и 2.

Примечание. Иногда существует несколько способов сочетания диаграмм посылок 1 и 2. Обязательно проверьте все возможные варианты.

При проверке всех возможных комбинаций помните, что существует пять возможных вариантов взаимного расположения двух кругов, а) А находится внутри В\ б) В находится внутри А, в) А и В частично накладываются друг на друга; г) А и В не накладываются друг на друга (два отдельных круга), и д) А и В полностью совпадают (изображаются одним кругом) Эти пять вариантов показаны на рисунке.

Давайте перейдем ко второму силлогизму А = родители В = понимают детей С = учителя

1. Ни один из родителей не понимает детей (Ни одно А не есть В).

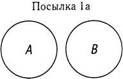
2. Некоторые учителя понимают детей (Некоторые С есть В)

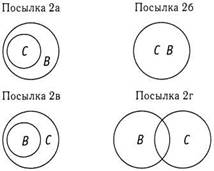
Ни один из родителей не является учителем (Ни одно А не есть С)

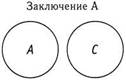
Поскольку посылка 1 является общеотрицательной, то для нее существует только один вариант диаграммы, и данная связь изображается в виде двух отдельных кругов. На диаграмме эта фигура обозначена 1а. Посылка 2 является частноутвердительной, что изображается на диаграмме с помощью четырех возможных фигур (2а, 2б, 2в и 2 г). Заключение является общим отрицанием, поэтому оно изображается одной фигурой в виде двух отдельных кругов. Теперь будем комбинировать 1а+2а, 1а+2б, 1а+2в и 1а+2 г. Как только вы найдете хотя бы одно сочетание, которое противоречит заключению, вы можете остановиться и принять решение о том, что заключение не валидно, или вам придется проверить все комбинации, чтобы прийти к выводу о валидности заключения.

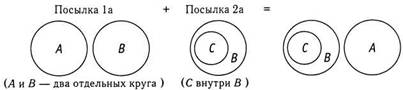
А и В — отдельные круги, и С находится внутри В. Продолжим!

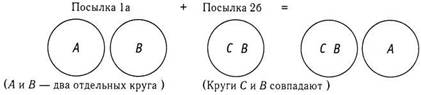
А и В — отдельные круги, и круги С и В совпадают. Продолжим!

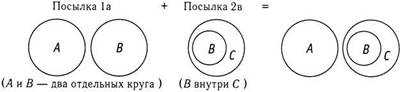
А и В — отдельные круги, и круги С и В совпадают. Хорошо, продолжим!

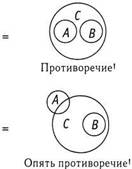
Существует несколько возможных сочетаний 1а и 2в, и нам надо проверить все способы взаимного расположения кругов, при которых А и В — два отдельных круга, и В находится внутри С. Если вы найдете хотя бы одну комбинацию 1 а+2в, которая противоречит заключению «Ни одно А не есть С», то вы можете прекратить процесс проверки комбинаций и сделать вывод о том, что заключение не валидно.

Остановимся на этом месте! Существует такое возможное размещение кругов, когда А и С не являются отдельными кругами. Заключение не валидно! На основе данных двух посылок мы не можем заключить, что «Ни один родитель не является учителем».

Ниже приводится разбор остальных трех силлогизмов. Поработайте над ними самостоятельно, не заглядывая в книгу, а потом сравните свою работу с приведенными примерами

А= юристы, В = умные С = богатые

1. Некоторые юристы не умны (Некоторые А не есть В)

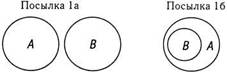
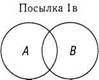
2. Некоторые умные люди богаты (Некоторые В есть С).

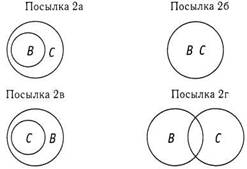
Заключение: Некоторые юристы богаты (Некоторые А есть С).

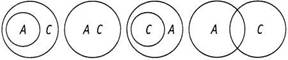
Чтобы проверить истинность заключения, проверьте сочетания 1а+2а, 1а+2б, 1а+2в, 1а+2 г, 1б+2а, 16+26, 1б+2в, 1б+2 г, 1в+2а, 1в+2б, 1в+2ви 1в+2 г.

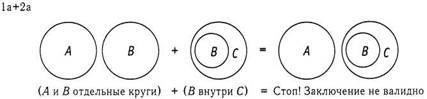
На основе данных двух посылок мы не можем заключить, что «Некоторые юристы богаты».

Следующая задача

А- физики; В = хорошо разбираются в математике; С = студенты.

1. Все физики хорошо разбираются в математике (Все А есть В).

2. Некоторые студенты являются физиками (Некоторые С есть Л).

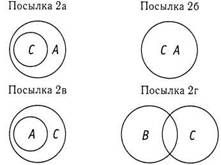
Некоторые студенты хорошо разбираются в математике (Некоторые С есть В).

Если вы понимаете, что делаете, то диаграмму для заключения рисовать не обязательно.

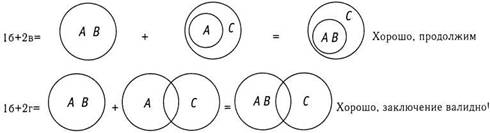
Следующая задача

1. Всем американцам необходима медицинская страховка (Все А есть В)

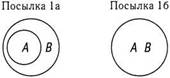
2. Все, кому необходима медицинская страховка, должны за нее голосовать

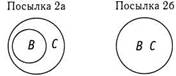
Заключение. Все американцы должны голосовать за медицинскую страховку (Все/1 есть С)

Вербальные правила проверки валидности заключения

Круговые диаграммы имеют одну любопытную особенность. Некоторые люди их любят, а некоторые — ненавидят. Главная проблема при работе с ними — это необходимость проверки всех возможных комбинаций диаграмм обеих посылок. Люди, предпочитающие пространственное мышление, «видят» комбинации с очевидной легкостью, в то время как те, кто предпочитает вербальные способы мышления, испытывают при этом большие трудности. Если вам трудно комбинировать посылки в виде соположения кругов, не падайте духом, потому что существуют и вербальные правила для проверки валидности заключения силлогизма. Эти правила действуют так же хорошо, как круговые диаграммы. Стернберг и Велл (Sternberg Well, 1980) обнаружили, что вербальные и пространственные методы требуют использования различных способностей, и эффективность конкретного метода зависит от того, какая модальность мышления доминирует у данного человека Существует пять правил для проверки валидности заключения. Чтобы использовать эти правила, надо изучить два дополнительных термина.

В силлогизме упоминаются три класса понятий, которые обозначены А, В и С или любыми другими названиями классов, которыми мы заменяем А, В и С в более конкретных примерах. Один из этих классов называется средним термином силлогизма. Чтобы определить, какой из терминов является средним, надо обратиться к заключению В заключении присутствуют два термина, один из которых является подлежащим, а другой — сказуемым. Средним термином является тот, который не упомянут в заключении Он называется средним термином потому, что связывает между собой другие два термина посылок. Вспомните силлогизм 1. Его заключение — «Некоторые люди, получающие социальные пособия, являются нечестными». В этом предложении «люди, получающие социальные пособия» — подлежащее, а «являются нечестными» — сказуемое. Средним термином является класс «бедные» Средний термин присутствует в обеих посылках, но отсутствует в заключении.

Второе понятие, которое необходимо ввести, — это распределенный термин. Термин распределен, если суждение относится ко всем элементам класса (Govier, 1985). Рассмотрите четыре типа отношений между классами, представленные в табл. 4.3. Для каждого я указала, какие из терминов распределены, а какие — не распределены. Как видно из табл. 4.3, распределены те классы, при которых есть определяющие слова «все», «ни одно» и частица «не».

Таблица 4.3. Распределенные и нераспределенные термины в четырех наклонениях силлогизмов

Обратите внимание на утверждение «Все А есть В». В этом утверждении термин В не распределен, потому что могут существовать некоторые В, которые не есть А, поэтому суждение не относится ко всем В. С другой стороны, рассмотрите суждение «Ни одно А не есть В». В этом случае термин В распределен, потому что, когда мы говорим «Ни одно А не есть В», мы также утверждаем, что «Ни одно В не есть А». Таким образом, во втором случае суждение относится ко всем В.

Для того чтобы заключение было валидным, силлогизм должен удовлетворять всем правилам, перечисленным в табл. 4.4. Если хотя бы одно требование не выполнено, заключение не валидно.

Давайте применим эти правила к силлогизмам, которые мы уже решили с помощью круговых диаграмм.

Силлогизм 1

А = люди, получающие социальные пособия, В = бедные; С = нечестные

Все люди, получающие социальные пособия, являются бедными (Все А есть В).

Некоторые бедные люди являются нечестными (Некоторые В есть С).

Некоторые люди, получающие социальные пособия, являются нечестными (Некоторые А есть С).

Средним термином силлогизма является В. Он упоминается в обеих посылках и отсутствует в заключении. Первое правило начинается со слов «если заключение отрицательно». Поскольку заключение данного силлогизма положительно, то можно сразу переходить ко второму правилу. Второе правило утверждает, что средний термин должен быть распределен хотя бы в одной из посылок. Давайте проверим его выполнение. Средним термином является В (бедные люди). Определен ли он словами «все» или частицей «не» хотя бы в одной посылке? Термин В не распределен ни в одной из посылок, поэтому мы можем остановиться. Заключение не валидно! Но вы, конечно, уже это знаете, потому что мы выяснили, что заключение этого силлогизма не валидно, когда проверили его с помощью круговых диаграмм.

Давайте применим вербальные правила ко второму силлогизму.

Таблица 4.4 Правила проверки валидности заключения рассуждений, содержащих кванторные слова:

1. Если заключение отрицательное, одна из посылок должна быть отрицательной, и наоборот, если одна из посылок отрицательна, заключение должно быть отрицательным

2. Средний термин должен быть распределен хотя бы в одной из посылок.

3. Любой термин, который распределен в заключении, должен быть распределен хотя бы в одной посылке.

4. Если обе посылки являются частными суждениями, то заключение не может быть валидным.

5. Если одна из посылок является частным суждением, заключение должно быть также частным суждением

6. Хотя бы одна посылка должна быть утвердительной (из двух отрицательных посылок нельзя сделать валидного заключения).

Силлогизм 2

А = родители; В = понимают детей; С = учителя

Ни один из родителей не понимает детей (Ни одно А не есть В).

Некоторые учителя понимают детей (Некоторые С есть В).

Ни один из родителей не является учителем (Ни одно А не есть С).

Первое правило гласит, что если заключение отрицательно, то хотя бы одна посылка должна быть отрицательна, и наоборот. Заключение отрицательно и отрицательна одна из посылок, поэтому мы можем переходить ко второму правилу.

Второе правило требует, чтобы средний термин был распределен хотя бы в одной из посылок. Какой из терминов является средним? Это термин, который не упомянут в заключении, т. е. В. Он распределен в посылке 1, поэтому мы можем двигаться дальше.

Третье правило говорит о том, что любой термин, распределенный в заключении, должен быть распределен хотя бы в одной из посылок. В заключении распределены оба термина — и А, и С. А распределен в посылке 1, но С не распределен ни в одной из посылок, поэтому можно остановиться. Заключение не валидно!

Ниже приводится краткая проверка остальных силлогизмов.

Силлогизм 3

А = юристы, В = умные; С = богатые.

Некоторые юристы не умны (Некоторые А не есть В).

Некоторые умные люди богаты (Некоторые В есть С).

Некоторые юристы богаты (Некоторые А есть С).

Нарушено 1-е правило, первая часть правила выполнена, поскольку заключение не является отрицательным, но вторая часть нарушена, потому что первая посылка отрицательна, а заключение положительно. Заключение не валидно!

Силлогизм 4

Все физики хорошо разбираются в математике (Все А есть В).

Некоторые студенты являются физиками (Некоторые С есть А).

Некоторые студенты хорошо разбираются в математике (Некоторые С есть В).

Правило 1 выполнено: отрицания отсутствуют.

Правило 2 выполнено: средним термином является А А распределен.

Правило 3 выполнено: ни один термин в заключении не распределен.

Правило 4 выполнено: одна из посылок не является частным суждением.

Правило 5 выполнено: одна из посылок является частным суждением, и заключение является частным суждением.

Правило 6 выполнено: одна из посылок утвердительная.

Заключение валидно!

Силлогизм 5

Всем американцам необходима медицинская страховка (Все А есть В).

Все, кому необходима медицинская страховка, должны за нее голосовать (Все В есть С).

Все американцы должны голосовать за медицинскую страховку (Все А есть С).

Правило 1 выполнено: отрицания отсутствуют.

Правило 2 выполнено: средним термином является В. В распределен.

Правило 3 выполнено: А распределен в заключении и в первой посылке.

Правило 4 выполнено: обе посылки являются общими, а не частными суждениями.

Правило 5 выполнено: ни одна из посылок не является частным суждением.

Правило 6 выполнено: одна из посылок утвердительная.

Заключение валидно!

Силлогизмы в повседневной жизни

Возможно, что во время чтения последнего раздела вы в какой-то момент сказали себе: «Стоит ли этим заниматься?» Может показаться, что силлогизмы — это искусственные задачи, придуманные исключительно для того, чтобы студенты и преподаватели не остались без работы. Если у вас возникала такая мысль, то, значит, вы сомневались в практической значимости силлогизмов. Практическая значимость концепции означает, что она истинна и находит применение не только в лаборатории или учебном классе, но и в обыденной жизни. Другими словами, возникает вопрос: пользуются ли люди силлогистическими рассуждениями в условиях обыденной жизни?

Силлогистические рассуждения, так же как и другие типы рассуждений — такие как линейное упорядочение и условные рассуждения, иногда считаются вспомогательными элементами при решении задач. Часто при решении мы начинаем с утверждений, которые являются или считаются истинными (посылок), а затем решаем, какое заключение можно вывести из них логическим путем.

Силлогизмы также встречаются в неявном виде в обычных текстах. Конечно, в этом случае посылки и заключения не выделены, но структура силлогизма во многом сохраняется. Легче всего найти силлогизмы в юридических и политических текстах, а также в стандартизированных тестах, предлагаемых при поступлении в колледжи, аспирантуру и юридические школы. Ниже приводится пример силлогистических рассуждений, которые больше похожи на силлогизмы, встречающиеся в повседневной жизни.

Следует признать смертную казнь неконституционной. Это самая жестокая из возможных форм наказания, кроме того, оно выходит за рамки обычных человеческих представлений. В Конституции есть специальная статья, защищающая нас от жестоких и выходящих за рамки обычных человеческих представлений наказаний.

Можно ли на основе этих утверждений заключить, что смертный приговор противоречит Конституции? Попробуйте переформулировать эти фразы, чтобы они приняли вид стандартного силлогизма (две посылки и заключение). Используйте круговые диаграммы или вербальные правила для проверки истинности этого заключения. Сделайте паузу и поработайте над этим силлогизмом из естественного языка.

У вас должен был получиться приблизительно такой силлогизм:

Посылка 1: Смертная казнь является жестоким и выходящим за рамки обычных человеческих представлений наказанием.

Посылка 2: Жестокие и выходящие за рамки обычных человеческих представлений наказания противоречат Конституции.

Заключение: Смертная казнь противоречит Конституции.

Если мы перейдем к терминам А, В и С, то получится примерно такая картина:

А = смертная казнь;

В = жестокое и необычное наказание;

С = противоречит Конституции.

Силлогизм примет вид:

Все А есть В.

Все В есть С.

--

Все А есть С.

В такой абстрактной форме этот силлогизм можно проверить с помощью либо круговых диаграмм, либо вербальных правил, и определить, действительно ли заключение логически следует из посылок. Этот пример иллюстрирует мысль о том, что силлогизмы часто присутствуют в повседневной аргументации. Часто мы не узнаем их, потому что на посылках и заключении нет аккуратных ярлычков, но если вы возьмете себе за правило искать их, то вас удивит, насколько часто они будут вам встречаться.

Опущенные кванторные слова

Если сейчас существует какое-либо равенство, то оно появилось в результате нашей борьбы за него. Потому что говорилось «все», а подразумевалось «некоторые». Слово «все» означает все.

Би Ричарде (Цит. по: Beilensen Jackson, 1992, p. 22)

В силлогизмах, встречающихся в обыденном употреблении, часто отсутствуют кванторные слова. Иногда их опускают специально, в надежде, что вы будете подразумевать определенное кванторное слово (например, «все» вместо более точного «некоторые»). Вот пример категорического силлогизма из недавней кампании по выборам президента. Кандидату на пост президента США (на предварительных выборах) задали вопрос о его изменах жене, ставших, благодаря прессе, общеизвестным фактом. Он отвечал следующим образом: «Моя частная жизнь не идеальна, но у нас были и другие великие президенты, которые также были далеки от идеала в частной жизни».

Давайте преобразуем эти рассуждения в категорический силлогизм:

Посылка 1: Я не идеален (в моей частной жизни).

Посылка 2: Некоторые великие президенты не были идеальны (в их частной жизни)

Заключение: Я буду великим президентом (подразумевается).

В абстрактной форме силлогизм имеет следующий вид:

А = я (говорящий);

В = люди, далекие от идеала;

С = великие президенты

ИЛИ

Все А есть В.

Некоторые С есть В.

Все А есть (будут) С.

Этот кандидат хотел, чтобы слушатели сделали вывод, что он тоже будет великим президентом. Проверьте валидность этого заключения либо с помощью круговых диаграмм, либо с помощью вербальных правил. Является ли подразумеваемое заключение валидным? Обратите также внимание на то, какие слова были выбраны для описания адюльтера (не идеален). Это тот же тип рассуждений, который применяется в комиксе про Кэлвина и Хоббса, приведенном на следующей странице.

В повседневной речи кванторные слова могут несколько отличаться от тех, которыми мы пользовались здесь. Вместо «все» могут быть использованы «каждый» и «любой», а вместо «некоторые» — «многие» или «немногие». Нетрудно заменить их кванторными словами, используемыми в этой книге, и затем проверить валидность заключения (Nickerson, 1986).

Вот пример, услышанный мной недавно в разговоре (я несколько отредактировала его):

«Люди, которые ходят на рок-концерты, курят травку. Джей ходил на рок-концерт. Следовательно, Джей курит травку». Валидность этого повседневного силлогизма зависит от того, считает ли говорящий, что «Все люди, которые ходят на концерты рок-музыки, курят травку» или что «Некоторые люди, которые ходят на концерты рок-музыки, курят травку». При понимании подобных утверждений важно указать, какое кванторное слово имеется в виду. Если подразумевается «некоторые», то можно сразу указать на то, что заключение «Джей курит травку» неправильно. Если подразумевается «все», то можно усомниться в правильности выбора кванторного слова.

Изменение установок с помощью силлогизмов

Основная структура умозаключения, состоящая из двух посылок и заключения, часто используется для изменения установок (attitudes). При использовании силлогизмов с такой целью первая посылка обычно содержит убеждение, вторая посылка является оценкой этого убеждения или реакцией на него, а заключение представляет собой установку (Shaver, 1981). Эта основная структура имеет следующий вид:

Посылка, содержащая убеждение

Оценочная посылка

Заключение, содержащее установку

Давайте рассмотрим конкретный пример (Shaver, 1981):

Предотвращение войны спасает жизни.

Спасение жизней — хорошее дело.

Следовательно, предотвращение войны — хорошее дело.

Со временем силлогизмы, содержащие установки, связываются друг с другом таким образом, что заключение одного силлогизма используется в качестве оценочной посылки для другого силлогизма.

Затраты на оборону способствуют предотвращению войны.

Предотвращение войны — хорошее дело.

Следовательно, затраты на оборону — хорошее дело.

Кэлвин и Хоббс.

Автор Билл Уатерсон

В этих силлогизмах средний термин (помните, что это означает?) становится доводом в пользу заключения. В целом, чем больше силлогизмов с одинаковым заключением кажутся нам истинными, тем сильнее поддержка заключения. Если бы я хотела, чтобы вы заключили, что затраты на оборону — хорошее дело, я могла бы также сообщить вам, что:

Затраты на оборону создают рабочие места

Создание рабочих мест — хорошее дело

Следовательно, затраты на оборону — хорошее дело

В этих силлогизмах кванторные слова присутствуют в неявном виде, но основная структура силлогизма сохраняется. Задача состоит в том, чтобы определить, следует ли заключение из посылок.

Распространенные ошибки в силлогистических рассуждениях

На данном этапе истории психологии, когда мы слышим утверждения о том, что машины могут думать, кажется странным говорить, что люди этого не могут

Церазо и Противера (Ceraso & Piolivera, 1971, р 400)

Исследования показали, что некоторые силлогизмы решаются труднее, чем другие. Анализ сделанных людьми ошибочных заключений показал, что ошибки можно отнести к четко разграниченным типам или классам. Одним из таких классов ошибок, которые я хочу рассмотреть, является неправильное обращение.

Неправильное обращение. Эта ошибка связана с изменением значения посылки. Большинство людей воспринимает посылки типа «Все А есть В» в том смысле, что верно также и утверждение «Все В есть A» (Chapman Chapman, 1959). Как вы теперь уже должны понимать, «Все А есть Б» и «Все В есть Л» — это не одно и то же. При трансформации посылки в неэквивалентую форму происходит ошибка, которую называют неправильным обращением. Если перейти к реальным высказываниям, то утверждение «все республиканцы голосовали за этот законопроект» не означает, что все голосовавшие за этот законопроект были республиканцами. Эти утверждения не эквивалентны.

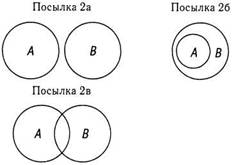
Еще один распространенный случай неправильного обращения имеет место, когда люди верят, что «Некоторые А не есть В» означает также, что «Некоторые В не есть Л». Второе утверждение не эквивалентно первому. Ниже приводятся круговые диаграммы для этих утверждений. Из них ясно видно, что эти утверждения не идентичны. Чтобы проиллюстрировать эту мысль, рассмотрим различия между утверждениями «Некоторым детям не сделали прививку» и «Некоторые их тех, кому сделана прививка, не являются детьми». Обратите внимание на различия между посылками 16 и 26.

А = дети; В = те, кому сделали прививку

1. Некоторые А не есть В. Некоторым детям не сделали прививку

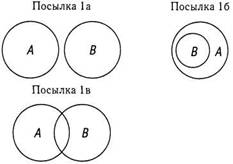
2. Некоторые В не есть А. Некоторые их тех, кому сделана прививка, не являются детьми.

Дизъюнктивные (разделительные) суждения

Рассмотрим две пары посылок:

Чак или красив, или знаменит.

Чак не знаменит.

Что вы можете заключить?

Чак или красив, или не знаменит.

Чак знаменит.

Что вы можете заключить?

Из обеих пар посылок следует одно и то же заключение — Чак красив. Многим людям кажется, что разобраться во второй паре посылок гораздо труднее. Посылки, имеющие структуру «или-или», также используются при рассуждениях и называются дизъюнктивными. Посылки такого типа легко можно переформулировать и представить в виде условных отрицательных утверждений, например, «если Чак красив, то он не знаменит».

В утверждениях типа «или-или» истинное значение имеет только один из двух (или нескольких) классов. Самый простой способ разобраться в таких рассуждениях — это нарисовать два символических представления возможных вариантов, а затем посмотреть, можно ли убрать одно из них. Ответом будет то, что останется.

Давайте попробуем сделать это для только что обсуждавшегося дизъюнктивного суждения: «Чак или красив, или знаменит».

Нарисуем два круга, каждый из которых представляет одно из возможных состояний.

Теперь прочитаем второе предложение «Чак не знаменит». Перечеркнем круг с пометкой «знаменит».

Остался круг с пометкой «красив». Следовательно, он красив. Теперь давайте попробуем сделать то же самое для более трудного второго примера: «Чак или красив, или не знаменит».

Нарисуем круги, изображающие эти два возможных состояния.

Теперь читаем второе предложение: «Чак знаменит». Поскольку он не может быть одновременно знаменит и не знаменит, вычеркиваем круг с пометкой «не знаменит».

Что осталось? Круг с надписью «красив». Это правильный ответ. Суждения типа «или-или» часто используются в рекламе. Вот одно из моих любимых рекламных объявлений:

Мы гарантируем вам низкие цены. Если вы сможете найти где-либо более низкую цену, то мы или продадим вам товар за такую же цену, или вы получите его бесплатно!

Вот так сделка! Сомневаюсь, что они предпочтут отдать мне товар бесплатно. А какова альтернатива? В рекламном объявлении можно было написать: «Мы согласны конкурировать с любой предложенной ценой». Но разве покупателю не покажется более выгодным вариант, когда ему либо продадут товар по той же цене, либо отдадут бесплатно? Конечно, здесь все дело в том, кто будет выбирать. Если бы выбирала я сама, то я бы взяла товар бесплатно, но я сомневаюсь, что в данном случае выбор оставят за покупателем.

Назад: Комбинаторное рассуждение

Дальше: Вероятностные рассуждения