Глава 4. Произвольность

Когда пишешь о мышлении, легко затеряться в путанице отвлеченных слов и понятий. В настоящей главе дастся реальный пример использования нешаблонного мышления, когда обычные мыслительные процессы прямо переводятся на наглядный язык, придающий смысл упражнениям по нешаблонному мышлению. Видимая запутанность используемых здесь фигур служит практическим целям, которые дают основу для более абстрактных описаний, используемых в дальнейшем.

Часть мира, которая образует непосредственное окружение человека, можно назвать ситуацией.

Или, если выразиться иначе, ситуацией следует считать то, что ранее было доступно непосредственному вниманию. Внимание в любой произвольно взятый момент времени может быть направлено только на часть ситуации. Результатом такого внимания является восприятие.

Восприятие состоит из информации, собранной каким-то числом различных чувств из той части окружения, на которую направлено внимание. Восприятию могут содействовать все органы чувств, хотя может оказаться достаточным и одного.

На приведена простая зрительно воспринимаемая ситуация. Она достаточно проста, чтобы восприниматься как целое, и, следовательно, рассматривается как единичное восприятие. Для восприятия этой ситуации требуется только зрение.

Простота этой ситуации и тот факт, что она поддается непосредственно визуальному восприятию, облегчает наблюдение за процессом мышления, хотя эта ситуация может выражать собой и другие, более сложные ситуации, для восприятия которых могут потребоваться наряду со зрением и другие органы чувств.

Ситуация имеет форму геометрической фигуры, достаточно простой, но все же незнакомой. Она неизвестна в том смысле, что не имеет определенного названия. Для ее описания недостаточно одного слова, как это имеет место в случае с квадратом, прямоугольником или крестом.

Фигура настолько проста, что ее, вообще говоря, можно определить как угодно. В ней как будто бы все понятно и доступно объяснению.

Основной задачей этого упражнения является не столько необходимость понять фигуру, сколько необходимость описать ее человеку, который ее не видит. Такое описание ситуации другому человеку аналогично его описанию самому себе, что и составляет процесс понимания любой ситуации.

Необходимость совершить действие является одной из наиболее важных причин, способствующих пониманию ситуации. В наших примерах требуемое действие заключается в необходимости описать кому-то предлагаемые фигуры.

Поскольку для описания данной фигуры нет однозначного эквивалента в обиходной речи и поскольку также единственно возможным способом описания являются только знакомые слова, нашей задачей является описать эту незнакомую геометрическую фигуру с помощью знакомых слов.

Итак, эта фигура может быть описана только посредством уже известных терминов. Ее, например, можно сравнить с какой-нибудь знакомой фигурой и описать их сходство и различие. Однако наиболее разумно расчленить незнакомую фигуру на знакомые составные части, назвать их и указать принцип их соединения.

На показан один из способов деления фигуры, представленной на . На основании такого деления фигуру можно описать в нескольких вариантах.

1. Два параллельных бруска, разделенных двумя короткими перекладинами, чуть отстоящими от концов брусьев.

2. Горизонтальная балка, удерживаемая на другой, такой же горизонтальной балке двумя вертикальными стойками.

3. Прямоугольник, у которого две короткие стороны слегка сдвинуты к середине.

Существует также масса других способов описания приведенного здесь принципа деления фигуры.

Деления производятся исключительно в уме, слушатель получает лишь описание составных частей фигуры и их соотношения, в результате чего он может представить себе всю фигуру. Это напоминает перевозку громоздкой машины, которую вынуждены разобрать на мелкие и более удобные для перевозки части и в таком виде отгрузить заказчику, приложив инструкцию по ее сборке.

Представленный на принцип деления фигуры совершенно произволен. На предлагается другой способ деления той же фигуры, которая в этом варианте может быть описана следующим образом: две фигуры, имеющие форму желобов, сверху и снизу разделены двумя поперечными перекладинами. Вся фигура представляет собой единую конструкцию одинаковой ширины.

На показан третий вариант деления фигуры, который можно описать так: две L-образные фигуры вложены одна в другую так, что образуют прямоугольник с двумя выступающими плечами, к которому приложены два коротких бруска, служащие продолжением более длинных частей L-образных фигур.

Такого рода описание несколько туманно и может привести к неправильному представлению фигуры. Его следует использовать только в том случае, если человек, описывающий фигуру, и слушатель знакомы с L-образной конструкцией. Описание любой ситуации зависит от наличия знакомых терминов, с помощью которых наблюдатель хочет ее описать, но ото не значит, что выбранный им способ описания является наилучшим.

Со временем те части, которые были выделены для облегчения описания или объяснения ситуации, приобретают самостоятельное существование.

Они продолжают существовать даже тогда, когда ситуация, благодаря которой они возникли, уже забыта. И чем с большим успехом их можно применить для описания других ситуаций, тем более они воспринимаются как самостоятельные единицы.

Таким образом, единицы, которые были созданы произвольно, благодаря своей полезности становятся настолько устойчивыми, что уже нельзя усомниться в их реальном существовании. Эта убежденность может стать тормозом на пути дальнейшего развития. Чтобы избежать этого, следует постоянно помнить о произвольной природе многих понятий, и не следует допускать, чтобы они продолжали существовать и после того, как их полезность отпала.

На показан еще один способ деления первоначальной фигуры на составные части.

Создается впечатление, что этот принцип деления включает значительно больше знакомых элементов, чем все предыдущие. Однако, пытаясь описать соотношение отдельных элементов так, чтобы потом их можно было собрать в целую фигуру, мы наталкиваемся на значительные трудности. При любом описании недостаточно перечислить имеющиеся знакомые элементы, помимо этого, нужно еще хорошо понимать их сочетание. Нередко использование знакомых элементов приводит к совершенно неизвестному сочетанию, отсюда крайне важно соблюдать баланс между степенью знания элементов и степенью знания их возможных сочетаний.

Деление неизвестной геометрической фигуры на известные элементы всегда субъективно.

Знакомые элементы произвольно вычленяются из первоначальной фигуры, поскольку в нашу задачу не входит определение элементов, первоначально составляющих фигуру. Важно дать удовлетворительное описание, а метод деления, который при этом был выбран, не имеет значения.

Не имеет также значения степень адекватности изложенного описания, поскольку всегда можно подобрать более адекватное. Но если мы удовлетворены первоначальным описанием (или объяснением), мы никогда этого не обнаружим, так как не будем заинтересованы в поисках более адекватных описаний.

До тех пор, пока отдельные элементы, созданные при произвольном делении первоначальной фигуры, соединяются должным образом, не имеет никакого значения, каким образом фигура делилась при ее описании. Если же требуется не описание, а объяснение фигуры, то предпочтительнее не складывать элементы, а исследовать их сами по себе. В этом случае способ деления может привести к существенному различию в объяснении фигуры. Не следует забывать, что мы сами произвольно создали элементы для лучшего понимания ситуации, а до момента их создания они вообще но существовали. Но мы тем не менее с легкостью поддается своему первоначальному убеждению, что ситуация в самом деле построена из этих элементов. Тот факт, что какую-то конструкцию можно расчленить на определенные составные элементы, еще не значит, что она была составлена из этих элементов. Очень часто произвольное создание элементов (как в случае с избранной нами фигурой) ошибочно принимается за четкое и ясное восприятие этих элементов и их выделение из Цельной конструкции. Такое произвольное деление называется анализом по составным элементам.

Все незнакомые ситуации всегда разбиваются на знакомые элементы. Для того чтобы иметь основание утверждать, что именно эти элементы приводят к правильному анализу неизвестной ситуации, необходимо исключить возможность появления другого, лучшего объяснения, ибо последнему, возможно, потребуется использовать другие, еще недостаточно известные элементы.

На показано деление фигуры на две части. Получившиеся при этом элементы более сложные, чем предыдущие, и могут быть описаны как 1-образные, или двутавровые, секции.

Сочетание этих элементов крайне простое — они зеркально симметричны друг по отношению к другу. Подобный принцип деления фигуры показывает, насколько выбор элементов может упростить их соотношение.

Мы показали пять способов деления для описания одной и той же фигуры. Существуют и другие способы деления, на которых мы останавливаться не будем, ибо все имеет свои пределы. Теперь возникает вопрос: какое из вышеприведенных описаний следует считать наилучшим?

Поскольку вся фигура делилась целиком и ни одна часть не исключалась из описания, то все описания являются закопченными. Каждое деление в равной степени произвольно. По-видимому, самое лучшее деление то, которое выражается самым достоверным описанием. Дополнительным соображением для оценки деления, по-видимому, является степень сложности словесной передачи того или иного описания: в одном случае для описания принципа деления может потребоваться всего лишь несколько слов, в другом — несколько фраз, и оба будут в равной мере надежными и достоверными. Короче говоря, самым лучшим делением будет то, которое является самым полезным, что бы под этим ни подразумевалось. Сам по себе ни один способ деления не лучше и не хуже других, но он может быть либо лучше, либо хуже в зависимости от конкретных условий.

К числу таких условий относится имеющийся в наличии запас знакомых элементов и их соотношений у человека, производящего описание. Эти условия предполагают также наличие запаса (или предположение о наличии) этих знакомых элементов и их соотношений у того человека, для которого описание предназначено. Например, если бы потребовалось описать фигуру, представленную на рис. 1, инженеру, то деление, показанное на , по-видимому, было бы наилучшим, поскольку термин секция двутавровой балки ему вполне понятен.

Произвольность процесса деления позволяет производить его целенаправленно, с учетом понимания слушателем.

Если геометрическая фигура () встречается в пашей практике достаточно часто, она становится знакомой и надобность в ее делении на известные элементы отпадает. Геометрическая фигура может стать настолько известной, что сама окажется пригодной для описания последующих незнакомых ситуаций.

Таким образом, набор знакомых фигур и их соотношений постоянно увеличивается. Однажды начавшись, этот процесс в дальнейшем развивается самостоятельно, поскольку незнакомые фигуры, объясненные с помощью уже знакомых, также в свою очередь становятся достаточно знакомыми для того, чтобы с их помощью можно было объяснять последующие незнакомые фигуры.

Чтобы стать знакомой, геометрическая фигура должна встречаться многократно, но для того, чтобы фигура приобрела какое-то значение, каждый раз должно повторяться некоторое связанное с этой фигурой свойство.

Сколь бы большой ни была модель, от нее всегда мысленно можно отделить определенные части, р подобной конфигурации могут иметься линии раздела, которые бросаются в глаза при делении.

На рис. 7, 8, 9 и 10 показаны четыре различные фигуры, которые достаточно просты, но не настолько, чтобы их можно было обозначить одним словом. И хотя каждая фигура отличается от другой, тем не менее все они могут быть описаны с помощью какой-то одной знакомой фигуры.

На легко заметить естественные линии раздела на более мелкие элементы. Так можно отделить Т-образный элемент верхней части, а основание в свою очередь разбить на два других Т-образных элемента.

Если теперь фигуру на рассматривать по тому же принципу деления, который применялся к фигуре на , мы обнаружим, что и здесь в качестве единицы деления может быть использован тот же Т-образный элемент.

При таких ограниченных условиях Т-образный элемент становится знакомым настолько, что с его помощью можно попытаться описать фигуры, показанные на и .

Если фигуры, изображенные на и , легко поддаются расчленению на Т-образные части, то этого нельзя сказать о фигурах, помещенных на и . Если бы мы вначале рассматривали , вполне возможно, что Т-образный элемент никогда не превратился бы в знакомую нам фигуру.

На рис. 11, 12, 13, 14 показано деление каждой представленной выше фигуры на ряд простых Т-образных элементов. На и знакомая фигура возникла скорее в результате непосредственного восприятия, а не за счет ее объяснения с помощью уже знакомых фигур. Но поскольку начало уже положено, число знакомых фигур может все более возрастать.

Хотя и подсказал возможность выделения Т-образного элемента, тем не менее это выделение произошло совершенно произвольно. Однажды созданный, Т-образный элемент утверждает себя, постоянно доказывая свою пригодность для объяснения других фигур, изображенных на , , , . Эта универсальная применимость Т-образного элемента дает ему право на самостоятельное существование в качестве принципа объяснения.

Однако следует признать тот факт, что, каким бы удобным ни было деление фигур на Т-образные элементы, тем не менее нельзя утверждать, что они первоначально были составлены из таких Т-образных частей.

Если бы для описания геометрической фигуры, показанной на , был выбран какой-то другой способ деления, то, вполне возможно, он оказался бы самым подходящим для описания именно этой конкретной фигуры, но был бы совершенно непригодным для создания элементов, пригодных для описания других фигур. Представленную на фигуру можно с одинаковым успехом описать как состоящую из горизонтального бруска, поддерживаемого в центре более короткой вертикальной стойкой, покоящейся в свою очередь на втором, более длинном, горизонтальном бруске, поддерживаемом двумя другими вертикальными стойками, чуть сдвинутыми от концов бруска к центру. Это описание в такой же степени правомерно, как и принцип деления на Т-образные элементы. Таким образом, хотя оба описания в равной степени адекватны, их полезность в целом в действительности может оказаться совершенно различной. Довольствоваться адекватностью одного описания за счет отказа от поисков других, возможно более адекватных, описаний — значит отвергать прогресс. Предположим, что при описании фигуры на мы выбрали принцип использования горизонтальных и вертикальных брусков, а затем, обратившись к , мы обнаружили наличие Т-образного элемента. Одни просто примут это к сведению и этим ограничатся, в то время как другие вернутся к , с тем чтобы выяснить возможность применения Т-образного элемента при описании представленной на нем фигуры. Казалось бы, здесь не может быть двух мнений, и подобное отношение к делу столь очевидно, сколь и необходимо, однако на практике, как правило, бывает иначе.

Многие ли сознательно пойдут на то, чтобы в свете новой информации пересмотреть те проблемы, которые уже нашли подходящее объяснение? Почему бы не применить Т-образный элемент, появившийся при одном способе деления, к описанию другой фигуры (например, на ), заменив ранее использованный здесь принцип деления? Значение Т-образного элемента возрастает с каждым новым удачным его применением, однако вначале его значение было ничуть не больше, чем любого другого элемента, полученного в ходе деления фигуры. Кто в силах отказаться от первоначального адекватного объяснения только для того, чтобы подобрать другое, равной степени адекватности?

Если же переосмысление исходной ситуации является для нас вполне естественным процессом, не менее естественной будет для нас и новая трактовка первоначальной фигуры (), на основе Т-образных элементов, предложенная на и .

Исходя из трактовки фигуры, показанной на рис. 16, можно сделать еще один важный вывод. Если бы нам представили исходную фигуру, вновь воспроизведенную на рис. 15, уже после того, как был создан Т-образный элемент, мы не задумываясь разделяли бы ее на эти элементы. Другие способы деления пас бы более не интересовали, и мы, возможно, даже препятствовали бы их появлению. Мы слишком быстро забыли, что, сколь бы адекватным ни было деление на Т-образные элементы, оно сделано произвольно и потому не исключает другие способы описания (или объяснения), которые, кстати, могут оказаться даже более эффективными.

Поскольку известность Т-образного элемента все более возрастает, мы невольно поддаемся искушению предпочесть это деление любому другому. При каждом новом удачном использовании Т-образного элемента его позиции все более укрепляются. Чем более полезным кажется элемент, тем чаще он используется, а чем чаще он используется, тем более кажется полезным.

Универсальная пригодность Т-образного элемента ведет к тому, что различные фигуры начинают рассматриваться как различные сочетания этого основного элемента. Каждая новая фигура предлагает свой образец соотношений Т-образных элементов. Вполне возможно, что эти соотношения были выведены из самой фигуры, однако следует помнить, что они были созданы под влиянием стремления рассматривать фигуру с точки зрения наличия в ней Т-образных элементов.

Благодаря постоянному использованию Т-образного элемента, количество его возможных сочетаний все более увеличивается, в то время как сам элемент остается неизменным. Кроме того, постепенно накапливаются незнакомые фигуры, которые благодаря применению Т-образных элементов становятся знакомыми.

На изображена довольно сложная фигура, которую для описания необходимо разбить на знакомые элементы. Расчленить эту фигуру на Т-образные блоки непросто. Однако если, кроме Т-образного элемента, мы не располагаем никаким другим известным элементом деления, то мы будем вынуждены, несмотря на трудности, описать, эту фигуру исходя из этого элемента.

На как раз и показано такое удачно выполненное деление, в результате которого вся фигура разбита на Т-образные элементы, что, по-видимому, может служить оправданием именно такого принципа деления, хотя (еще раз напоминаем), оно является чисто произвольным. Каждый человек обладает определенным запасом знакомых фигур; это обстоятельство не должно, однако, ограничивать способы описания фигур другими лицами, которые имеют собственный запас знакомых фигур.

Если на основе Т-образного деления, показанного на , мы попытаемся описать фигуру на , то вскоре обнаружим, что описать множество соотношений, определяющих расположение Т-образных элементов на этой фигуре, крайне трудно. И хотя Т-образный элемент сам по себе несложен, его соотношения в данной фигуре настолько сложны, что их описание становится почти невозможным.

На также изображена довольно сложная фигура (но более простая, чем на ). Можно опять попробовать описать ее с помощью Т-образных элементов и лишний раз убедиться, что такое описание вполне осуществимо. Однако соотношение Т-образных элементов при таком описании будет по-прежнему сложным.

Описание можно упростить, если фигуру разделить не на Т-образные, а на 1-образные элементы, как это показано на . Взаимоотношение трех получившихся при этом 1-образных элементов очень простое. Разумеется, каждый из 1-образных элементов представляет собой два Т-образных элемента, соединенных по основаниям.

Чем более крупные элементы деления фигуры, тем проще их соотношения. Так, на смену основным Т-элементам приходят их стандартные соединения. В некоторых случаях большие блоки выполняют функции основных элементов деления без каких бы то ни было ссылок на то, что они составлены из Т-образных элементов.

Выше было высказано предположение, что, чем сложнее элементы деления, тем проще их соотношения; и наоборот, чем проще основные элементы, тем сложнее их соотношения.

Следовательно, необходимо поддерживать баланс между простотой составных элементов и простотой их соотношений. Создание стандартных блоков из основных элементов решает эту проблему, так как использует более крупные элементы, которые в то же время остаются простыми.

Таким образом, достигается простота в описании как составных элементов, так и их соотношений.

Стандартные блоки из основных Т-образных элементов весьма полезны в случае необходимости упрощения описания сложных фигур, однако в отличие от собственно Т-образных элементов такие блоки используются в описании только ограниченного числа случаев.

Гибкость и универсальная пригодность Т-образного элемента дает ему право на существование вне зависимости от того, сколько стандартных блоков возникло на его основе. Если вдруг будет забыт Т-образный элемент, то нехватка составленных из него блоков для объяснения фигур может затруднить описание. Чем проще элемент деления, тем шире он может быть использован, поэтому желательно всегда иметь в запасе в качестве знакомых фигур не только основной Т-образный элемент, но и его сочетания в более крупные блоки.

Понять незнакомую ситуацию — дело довольно трудное, даже в тех случаях, когда есть возможность исследовать всю ситуацию целиком, а имеющиеся в наличии знакомые фигуры могут быть опробованы в знакомых соотношениях. Но еще более трудно понять ситуацию тогда, когда часть ее скрыта и недоступна исследованию, что нередко объясняется несоответствием приборов и методов исследования предъявляемым им требованиям. Приборы есть не что иное, как устройства для преобразования какого-то явления, недоступного органам чувств, в форму, доступную для восприятия. В других случаях часть незнакомой ситуации может оказаться недоступной для исследования потому, что необходимые для этого усилия на каким-то причинам нельзя произвести.

Случается также, что какая-то часть ситуации просто не в состоянии предоставить информацию.

Каковы бы ни были причины недоступности ситуации, необходимо попытаться понять всю ситуацию целиком путем тщательного изучения того, что доступно исследованию. Для объяснения скрытой части ситуации строятся пробные догадки, предположения и гипотезы.

На показана геометрическая фигура, часть которой скрыта от нас бесформенным пятном.

Предположим, что данная фигура столь же проста, как и прежние фигуры.

На основании тщательного исследования и измерения тех участков фигуры, которые выступают из-под пятна, можно строить различные догадки и предположения р том, что представляет собой вся фигура. Можно прибегнуть к различным сочетаниям Т-образного элемента, и если одно из сочетаний совпадает с видимой частью фигуры, то оно, возможно, совпадет со всей фигурой.

На показано удачное сочетание Т-образных элементов, которое полностью совпало бы с выступающими частями предыдущей фигуры. Испробовав все прочие возможные комбинации Т-образных элементов, мы убедимся, что предложенное на сочетание является единственно возможным для объяснения фигуры на . По-видимому, такая комбинация является точным отображением скрытой под пятном фигуры. Если удалить пятно, то под ним откроется именно эта фигура.

Последнее заключение относится к такому виду естественного предположения, которым обычно сопровождается появление гипотез. И хотя только одним сочетанием Т-образных элементов можно правильно объяснить форму замазанной пятном фигуры, однако пот никаких оснований предполагать, что эта фигура обязательно должна делиться на Т-образные элементы. В данном случае Т-образный элемент оказался полезным элементом описания, который, возможно, был единственным имеющимся в наличии знакомым элементом. Однако ни одно из этих обстоятельств но меняет его произвольного характера. Этот элемент существует только ради удобства. Форма новой фигуры не обязательно должна соответствовать чисто произвольному способу описания ситуации. Однако вера в полезность Т-образного элемента, испытанная на практике, может легко навести на мысль о необходимости такого соответствия. Вполне возможно, что другой человек, имея в наличии другую знакомую фигуру, решит, что замазанная фигура должна быть объяснена именно с помощью этой известной ему фигуры.

Действительно, каждый человек формулирует единственно возможную гипотезу, используя имеющиеся знакомые фигуры (в данном случае Т-образный элемент). Тем не менее такая гипотеза, сколь бы точно она ни формулировалась на языке Т-образных элементов, всего лишь предполагает (но не доказывает), что данная фигура должна иметь именно такую форму.

Единственным доказательством гипотезы является ее полезность, и, пока полезность продолжает иметь место, гипотеза остается в силе. Однако даже полезность не должна препятствовать поискам лучшей гипотезы, которая, возможно, будет использовать при описании другие знакомые фигуры.

Когда мы описывали вышеприведенные фигуры, полностью доступные восприятию, мы могли использовать любой метод описания, однако, когда мы имеем дело с частично закрытыми фигурами, любая примененная в этом случае гипотеза может оказаться непригодной.

Одной из главных задач мышления является необходимость постоянного уяснения разного рода незнакомых ситуаций. Как правило, имеется некоторая фигура, которую требуется уяснить с помощью сочетания уже знакомых фигур. Сочетание знакомых фигур всегда направлено к какому-то практическому результату, в котором постоянно используется все увеличивающийся набор знакомых фигур и их соотношений.

Однако существует и другой метод использования знакомых фигур. Фигуры могут быть составлены совершенно произвольно, по любому образцу или же на основании законов гармонии. Подобные сочетания составляются исключительно ради самих сочетаний.

Такого рода игра со знакомыми фигурами, казалось бы, абсолютно бесцельна, и тем не менее она может оказаться весьма полезной. В ходе игры могут возникнуть интересные сочетания, которые дополнят список знакомых фигур и будут в такой же степени полезными, как и те, что были получены в ходе описания незнакомых фигур. Фигуры, случайно полученные в процессе игры, могут помочь объяснить фигуры, которые ранее но были объяснены. Процесс игры, строящейся на чистом случае, нередко приводит к таким сочетаниям, которых, быть может, никогда бы не удалось достичь каким-либо иным путем.

На , и приведены сочетания обычных Т-образных элементов, возникшие в ходе игры.

Эти сочетания получились без всякого намерения или заранее обдуманного плана; кроме того, каких-то особых причин для отбора именно этих сочетаний из неограниченного количества других не было.

Из соединения этих сочетаний получились фигуры, показанные на , и . Эти фигуры интересны сами по себе, и, не будь они собраны нами из Т-образных элементов, нам было бы нелегко объяснить их на языке этих элементов.

Как фигуры, появившиеся из игровых сочетаний Т-образных элементов, пополнили список незнакомых фигур, так и их соотношения, возникшие таким же образом, пополняют свой список. В игре мы имеем возможность выявить и испробовать новые соотношения фигур и узнать о соотношениях, возникших случайно.

Игра очень полезна также и в том отношении, что она является источником появления знакомых фигур и их соотношений и источником опыта и познания. Оригинальность фигур и их соотношений, возникающих случайно во время соответствующей игры, обычно превосходит оригинальность фигур и их соотношений, которые возникают в ходе объяснения реально существующих ситуаций. Случай не знает границ, тогда как воображение ограничено.

Даже когда полезность игры не вызывает сомнений, людей, способных играть, крайне мало.

Трудно намеренно делать то, что не должно быть намеренным, так же трудно, как идти в никуда.

На изображена еще одна геометрическая фигура, большая часть которой закрыта темным пятном.

На этот раз по сравнению с предыдущим еще большая часть фигуры недоступна исследованию.

Весьма сомнительно, можно ли вообще получить какие-то сведения о данной фигуре из исследования ее видимых участков. Мы имеем возможность, как и раньше, испробовать множество различных гипотетических сочетаний основного Т-образного элемента. Поскольку в нашем распоряжении имеется большое количество предполагаемых сочетаний, на первый взгляд полностью совпадающих с рисунком, мы не в состоянии сказать определенно, какое из этих сочетаний следует использовать. Поэтому мы еще и еще раз вынуждены обращаться к скрытой под пятном фигуре и внимательно ее изучать. В результате мы убеждаемся, что для фигуры, изображенной на , сочетание Т-образных элементов, по-видимому, неприменимо.

предлагает наиболее вероятное приближение к фигуре, показанной на , которое можно получить из Т-образных элементов. Однако мы видим, что составленная фигура не идентична той, которая изображена на . Но если все же необходимо иметь какую-то гипотезу (иногда ради того, чтобы начать действовать), то в таком случае любое более или менее объясняющее ситуацию приближение может оказаться оправданным. Наряду с полезностью такой приближенной гипотезы, всегда есть надежда, что в дальнейшем, по мере использования, ее можно будет или усовершенствовать, или заменить другой. Разумеется, если требуется решить какую-то проблему, то просто бессмысленно ожидать появления лучшей гипотезы, вместо того чтобы начать действовать, используя любую гипотезу. Но в то же время иногда, быть может, лучше ничего не делать, чем делать не то, что надо (при условии, конечно, что само бездействие не является ошибкой). Основная опасность использования гипотезы, которая наверняка но соответствует действительности, заключается в том, что она может препятствовать появлению лучшей. Благодаря постоянному применению и некоторой доли полезности такой гипотезы ее несоответствие действительной ситуации постепенно забывается, поскольку живое сравнение с первоначальной ситуацией также вскоре забылось.

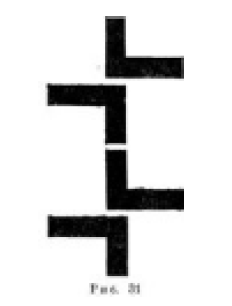
Когда с фигуры на удалили пятно, то под ним оказалась фигура, представленная на . Она состояла не из знакомых нам Т-образных, а из L-образных элементов. Возможно, нас уличат в нечестности, так как единственно знакомыми фигурами, которые были допущены в нашей игре, были Т-образные элементы. Но если отвлечься от этого обвинения, то введение L-образного элемента свидетельствует об одном очень существенном моменте, на который указывает также сам факт уличения нас в нечестности.

Дело в том, что L-образный элемент не является чем-то существенно отличным от Т-образного. Он совсем не нов и достаточно известен. На показано, что его легко получить из Т-образного элемента простым отсечением одного плеча.

Таким образом, Т-образный элемент потенциально содержал в себе L-образный.

Элемент Т — не священный и не неизменный, хотя тот факт, что он постоянно и повсеместно успешно применялся, мог привести к такому предположению. Т-образный элемент всегда был и остается произвольно созданным в целях удобства; разбивая на него незнакомые фигуры, мы имеем возможность описать их. Как более крупный блок можно разбить на Т-образные элементы, так и сам Т-образный элемент можно произвольно разбить на более мелкие части.

Выше мы показали, каким образом несколько Т-образных элементов можно объединить в стандартные блоки, с тем чтобы получить более крупные основные элементы, облегчающие описание сложных фигур. Было указано, что эти более крупные элементы в силу их громоздкости обладают меньшей универсальной полезностью, чем собственно Т-образный элемент.

Аналогичным образом и сам Т-образный элемент можно рассматривать как стандартное соединение L-образного элемента с коротким бруском. Бывают случаи, когда и это стандартное соединение оказывается слишком крупным и непригодным для описания, поэтому его следует разбить на более мелкие элементы с более широкой сферой применения. Таким образом Т-образный элемент сам может быть разбит на составные части.

Как сборка Т-образного элемента в более крупные блоки, так и разбивка его на более мелкие составные части вполне допустимы, поскольку первоначальный выбор этого элемента в качестве знакомой фигуры был произвольным. Если бы мы выбрали первоначально L-образный элемент, тогда Т-образный блок был бы производным от этого элемента. Любая незнакомая фигура с одинаковым успехом могла бы быть описана как с помощью Т-образного элемента, так и посредством сочетания L-образных элементов и коротких брусков. Однако описать соотношение таких элементов было бы, по-видимому, затруднительно.

Нелегко отказаться от знакомых фигур, неоднократно доказавших свою полезность. В таких случаях нас часто связывает чувство долга по отношению к этим фигурам. Мы быстро забываем о произвольной природе фигуры, которую теперь воспринимаем как открытие, в то время как она была создана просто для упрощения описания. Каждый раз, когда мы оказываемся перед необходимостью описать какую-то незнакомую фигуру, мы тратим много усилий на то, чтобы перепробовать всевозможные сочетания хорошо знакомых фигур, вместо того чтобы взять новую фигуру. Но с течением времени с необходимостью возникает вопрос о природе самих знакомых фигур, а не о том, как они складываются для объяснения ситуации.

И действительно, сколько ситуаций остались недопонятыми только потому, что их упорно пытались объяснить с помощью хорошо знакомых фигур, которые сами нуждались в перепроверке!

На показано, как можно разделить Т-образный элемент на четыре одинаковых бруска, собранных в виде буквы Т. С помощью таких брусков мы могли бы объяснить любую фигуру, которую ранее объясняли бы, используя Т-образный элемент, а сам Т-образный элемент рассматривать как стандартное соединение этих брусков.

На рис. 34 показано, как можно разделить на эти бруски первоначальную фигуру ().

Такое деление можно было бы произвести с самого начала, однако сложные соотношения большого количества маленьких брусков сделали бы описание фигуры значительно менее удобным, чем описание с помощью Т-образных элементов. Как только Т-образный элемент был установлен и использован на первой стадии описания, нам следовало бы пойти дальше и показать, каким образом для тех же целей можно использовать прямоугольные бруски, которые благодаря своей простоте должны найти более широкое применение. По мере упрощения основного элемента растет количество фигур, которые можно описать с его помощью. Запас стандартных соединений основного элемента облегчает описание других составленных из него сложных фигур.

Подобный процесс происходит при росте научных знаний, а точнее, при увеличении любых знаний.

Как только накапливается достаточная информация, появляется полезная стандартизирующая теория, аналогичная Т-образному элементу, которая оказывается вполне пригодной для объяснения явления. По мере усложнения явлений вводится применение стандартных сочетаний первоначальной теории. Наконец, встречается такая ситуация, которую становится невозможно объяснить с помощью первоначальное теории или посредством ее стандартных соединений. И тут неожиданно появляется более простая и более универсальная теория; в результате выясняется, что первоначальная теория была всего лишь производной от этой универсальной. Благодаря своей простоте новая теория объясняет все наблюдаемые явления.

Мы не стали описывать первоначальную фигуру (см. рис. 1) с помощью маленьких прямоугольных брусков, поскольку такое сложное описание было бы преждевременным. К тому же мы еще не располагали запасом необходимых соотношений фигур для такого описания. Нам потребовалось пройти две вспомогательные стадии, прежде чем прийти к мысли использовать для описания бруски: первая, несложная, стадия — деление на Т-образные элементы, вторая, столь же простая, — деление самих Т-образных элементов.

Нередко создается впечатление, что нет необходимости делить сам Т-образный элемент, поскольку не возникает ситуация, показывающая его неадекватность. И действительно, пока такая ситуация не появилась, Т-образный элемент с полным основанием можно считать наиболее простым основным элементом.

Существует масса ситуаций, анализ которых доведен до стадии деления на Т-образные элементы и к которым требуется применить дальнейшие стадии процесса деления. Даже вышеуказанный брусок не является окончательной элементарной частицей деления, поскольку может быть разделен на два квадрата, и так далее.

Таким образом, описания, начатые с использования весьма крупных субфигур и их простых соотношений, закончились использованием небольших и универсальных элементов, также связанных между собой весьма просто. Однако эта простота отношений была достигнута только после того, как были пройдены стадии появления стандартных соединений основных элементов, затем стандартных соединений стандартных соединений и так далее. Квадрат становится прямоугольным бруском, брусок — Т-образным элементом, Т-образный элемент — L-образным блоком.

На всех этих стадиях элементы описания произвольны, и, хотя они могут быть весьма полезными, упорно придерживаться их при описании не рекомендуется, поскольку это может препятствовать появлению лучшего варианта описания.