Приложение 2

Г.А. Лоренц

ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ В СИСТЕМЕ, ДВИЖУЩЕЙСЯ С ЛЮБОЙ СКОРОСТЬЮ, МЕНЬШЕЙ СКОРОСТИ СВЕТА

(Извлечения)

1. Стараясь на основании теоретических соображений определить влияние, которое может оказать поступательное движение (например, поступательное движение, испытываемое всеми системами вследствие годового движения земли) на электрические и оптические явления, мы сравнительно просто достигаем цели в тех случаях, когда рассматриваются только величины, пропорциональные первой степени отношения скорости поступательного движения w к скорости света с.

Случаи же, в которых могут быть обнаружены величины второго порядка, следовательно, порядка представляют более значительные трудности. Первым примером явлений этого рода является известный интерференционный опыт Майкельсона, отрицательный результат которого привел Фицджеральда и меня к заключению, что размеры твердых тел немного изменяются вследствие их движения через эфир.

…

2. Описанные опыты не являются единственным основанием желательности новой обработки проблем, связанных с движением земли. Пуанкаре, возражая против прежней теории оптических и электрических явлений в движущихся телах, указывал, что для объяснения отрицательного результата опыта Майкельсона оказалось нужным ввести новую гипотезу, и что в этом может встретиться необходимость каждый раз, когда станут известны новые факты. Подобному введению особых гипотез для каждого нового опытного результата присуща, конечно, некоторая искусственность. Положение вещей было бы удовлетворительнее, если бы можно было с помощью определенных основных допущений показать, что многие электромагнитные явления строго, т. е. без какого-либо пренебрежения членами высших порядков, не зависят от движения системы. Несколько лет тому назад я уже сделал попытку создать подобную теорию. Теперь я надеюсь рассмотреть этот вопрос с большим успехом. На скорость налагается только то ограничение, что она должна быть меньше скорости света.

…

Примечание Лоренца на с. 22 сборника: Можно заметить, что в этой статье мне не удалось в полной мере получить формулы преобразования теории относительности Эйнштейна. Ни равенство (7) ни формулы (8) не имеют того вида, который дан Эйнштейном, вследствие чего мне не удалось уничтожить член

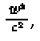
из первой формулы (9) и таким образом привести уравнения (9) точно к виду, справедливому для покоящейся системы. С этим обстоятельством связана беспомощность некоторых дальнейших рассуждений в этой работе.

Заслуга Эйнштейна состоит в том, что он первый высказал принцип относительности в виде всеобщего строго и точно действующего закона.

К этому я добавлю еще, что Фохт уже в 1887 г. (Gottinger Nachrichten, стр. 41) в работе «Uber das Dopplersche Prinzip» применил к формулам вида

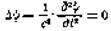
преобразование, которое эквивалентно преобразованию, содержащемуся в равенствах (4) и (5). [Примечание Г. А.Лоренца, 1912 г.].

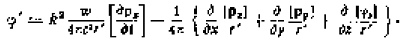
В этом уравнении все заключенные в скобки величины должны быть взяты для того момента, когда местное время центра частицы равно

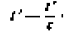
Мы заканчиваем эти соображения введением нового вектора р', компоненты которого равны:

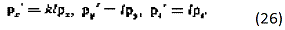
Одновременно мы переходим к х',у' z', t' как независимый переменным. Окончательный результат имеет вид:

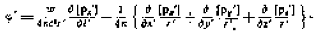
8. До сих пор мы пользовались только основными уравнениями, не вводя новых предположений. Теперь я допущу, что электроны, которые в состоянии покоя рассматриваются как шары радиуса R, изменяют свои размеры под влиянием поступательного движения, а именно: размеры в направлении движения уменьшаются в kl раз, а размеры в перпендикулярных к движению направлениях в l раз.

При этой деформации, которую мы обозначим через

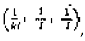
каждый элемент объема должен сохранить свой заряд.

Наше допущение ведет к тому, что в электростатической системе Σ, которая движется со скоростью w, все электроны преобразуются в эллипсоиды, малые оси которых лежат в направлении движения. Если мы теперь подвергнем систему деформации (kl, l, l) для того, чтобы иметь возможность применить теорему, изложенную в § 6, мы снова получим шаровые электроны радиуса R. Если мы, далее, изменим относительное положение электронных центров в Σ посредством деформации (kl l,l) и в полученные таким образом точки поместим центры покоящихся шаровидных электронов, то получим систему, которая будет тождественна воображаемой, описанной в § 6, системе Σ. Силы в этих двух системах связаны друг с другом соотношением (21).

Во-вторых, я принимаю, что силы, действующие между незаряженными частицами, так же, как и силы, действующие между незаряженными частицами и электронами, вследствие поступательного движения подвергаются изменению точно таким же образом, как электрические силы в электростатической системе.

Иными словами: какова бы ни была природа частиц весомого тела, всегда – при условии, что частицы не двигаются друг относительно друга – силы, действующие в покоящейся системе Σи в движущейся системе Σ связаны друг с другом соотношением (21), если, в смысле взаимного положения частиц система Σполучается из Σ посредством деформации (kl, l, l) и, следовательно, Σ из Σпосредством деформации

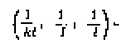
Легко видеть, что гипотеза, выдвинутая раньше в связи с опытом Майкельсона, содержится в высказанной теперь. Последняя гипотеза имеет, однако, более общий характер, потому что единственное ограничение движения заключается теперь в том, что скорость его должна быть меньше скорости света.

…

Но всякое изменение в движении системы влечет за собой соответствующее изменение в электромагнитном количестве движения и требует поэтому определенной силы, величина и направление которой дается формулой

Уравнение (28) можно строго говоря применять только к случаю равномерного и прямолинейного поступательного движения. Вследствие этого теория быстропеременных движений электрона очень трудна, хотя формула (29) всегда имеет место. Это обстоятельство усугубляется тем, что гипотеза § 8 включает требование, чтобы величина и направление деформации непрерывно изменялись. Едва ли вообще вероятно, чтобы форма электрона определялась одной только скоростью в рассматриваемый момент времени.

…

10. Мы можем теперь перейти к исследованию влияния движения земли на оптические явления в системе прозрачных тел. При этом мы обратим наше внимание на переменные электрические моменты в частицах или «атомах» системы. Мы можем применить к этим моментам рассуждения § 7. С целью упрощения мы полагаем, что в каждой частице заряд сосредоточен в определенном числе отдельных электронов. Пусть, далее, «упругие» силы, которые действуют на какой-нибудь один из этих электронов и совместно с электрическими силами определяют его движение, имеют свой исходный центр действия в точке, лежащей внутри границы того же атома.

Я покажу теперь, что каждому возможному состоянию движения в неподвижной системе можно сопоставить соответствующее, также возможное, состояние движения в системе, находящейся в поступательном движении, причем способ сопоставления характеризуется следующим образом.

Если мы исходим из некоторого действительно существующего состояния в системе Σ , то очевидно, что пользуясь положениями а) и б), мы вполне определяем некоторое состояние движущейся системы Σ. Вопрос о том, является ли это состояние также возможным, остается, однако, открытым.

Для того чтобы решить это, мы сначала заметим, что электрические моменты, которые по нашему допущению возникают в движущейся системе и которые будут обозначаться через р, суть определенные функции координат х, у, z центров А частиц (или, как мы будем говорить, координат частиц) и времени t. Уравнения, которые выражают связь между р, с одной стороны, и х, у, z, t, с другой, – могут быть заменены другими уравнениями, которые содержат вектор р', определяемый из формулы (26), и величины х, у, z, t, которые даются формулами (4) и (5).

Если в частице А движущейся системы, координаты которой суть х, у, z, в момент времени t или в момент местного времени t' имеется электрический момент р, то, согласно допущениям а) и б) в другой системе в частице с координатами х, у, z, и в момент истинного времени t' будет существовать электрический момент, который как раз будет представлен вектором р', определяемым по формуле (26). Таким образом, отсюда видно, что уравнения, связывающие р', х, у, z, t, будут одни и те же для обеих систем с тем единственным отличием, что для системы Σ без поступательного движения эти буквы означают электрический момент, координаты и истинное время, в то время как для движущейся системы они имеют другое значение. Ибо здесь р', х, у, z, t связаны с электрическим моментом р, с координатами х, у, z и с общим временем t соотношениями (26), (4) и (5).

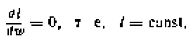
Константа должна иметь значение 1, потому что мы уже знаем, что при w = О значение l = 1.

Это ведет к предположению, что влияние поступательного движения (как для отдельного электрона, так и весомого тела в целом) простирается только на размеры в направлении движения, а именно: последние делаются в k раз меньше по сравнению с состоянием покоя.

Присоединив эту гипотезу к высказанным прежде, мы можем быть уверены в том, что возможны два состояния, одно – в движущейся системе, другое – в такой же но покоящейся системе, которые соответствуют друг другу указанным образом. Впрочем, это соответствие не ограничивается электрическими моментами частиц. В соответствующих точках, которые лежат либо в эфире между частицами, либо в эфире, окружающем весомые тела, мы находим для соответствующих моментов времени тот же вектор dи, как легко показать, тот же вектор h'. Резюмируя, можно сказать: когда в системе без поступательного движения возникает состояние движения, для которого в определенном месте компоненты векторов р, d и h являются определенными функциями времени, тогда в той же системе, после того как она приведена в движение (и, следовательно, деформирована), может возникнуть состояние движения, при котором в соответствующем месте компоненты векторов р', d', h' будут теми же функциями местного времени.

…

Только что сделанные выводы подтверждают прежние результаты, полученные с помощью соображений, в которых пренебрегалось величинами второго порядка. Эти же выводы содержат также объяснение отрицательного результаты опыта Майкельсона, причем более общее, и по форме несколько отличное от прежде данного. Они показывают далее, почему Рэлей и Брэс не могли наблюдать никаких признаков двойного лучепреломления, вызванного движением земли. Отрицательный результат опытов Трутона и Нобля делается тотчас же ясным, когда мы обратимся к гипотезам § 8. Эти гипотезы, а также наше последнее допущение (§ 10) позволяют заключить, что поступательное движение вызывает одно только сокращение всей системы электронов и других частиц, из которых построены заряженный конденсатор, коромысло и нить крутильных весов. Такое сокращение не дает, однако, никакого повода к заметному изменению направления.

Едва ли нужно отмечать, что я предлагаю эту теорию со всей осторожностью. Хотя она, по моему мнению, отвечает всем твердо установленным фактам, тем не менее эта теория приводит к некоторым следствиям, которые еще нельзя подкрепить опытом. Например, из теории следует, что результат опыта Майкельсона должен оставаться отрицательным, если пропустить интерферирующие лучи света через весомое прозрачное тело.

О нашей гипотезе сокращения электронов нельзя заранее утверждать ни того, что она правдоподобна, ни того, что она недопустима. Наше знание природы электронов еще весьма недостаточно, и единственным средством продвижения вперед является проверка гипотез, подобных предложенным мною здесь. Естественно, при этом возникают трудности, например, при рассмотрении вращения электронов. Может быть, мы должны будем допустить, что в тех явлениях, при которых в покоящейся системе шаровидные электроны вращаются вокруг одного из диаметров, в движущейся системе отдельные точки электронов описывают эллиптические орбиты, которые указанным в § 10 образом соответствуют круговым орбитам покоящегося случая.

12. Мы должны еще сказать несколько слов о молекулярном движении. Можно думать, что тела, у которых оно имеет заметное или даже преобладающее влияние, также подвержены тем же деформациям, что и системы с неизменным относительным положением частиц, о которых мы до сих пор говорили. В самом деле, мы можем вообразить себе в двух молекулярных системах Σ и Σ, из которых только вторая находится в поступательном движении, такие соответствующие друг другу молекулярные движения, что когда какая-нибудь частица в Σ имеет определенное положение в определенный момент времени, частица в Σ в соответствующий момент времени занимает соответствующее положение. Представив себе это, мы можем применять соотношение (33) между ускорениями во всех тех случаях, когда скорость молекулярного движения очень мала по сравнению с w. Тогда можно считать, что молекулярные силы определены относительным положением, независимо, от скоростей молекулярного движения. И, наконец если мы себе представим эти силы ограниченными столь малыми радиусами действия, что для действующих друг на друга частиц можно пренебречь разностью отсчетов местных времен, то данная частица вместе с теми, которые лежат в сфере ее притяжения или отталкивания, образует систему, претерпевающую неоднократно упомянутую деформацию. На основании второй гипотезы § 8 мы можем поэтому применить формулу (21) к результирующей молекулярной силе, приложенной к частице. Следовательно, правильное соотношение между силами и ускорениями будет иметь место в обоих случаях, если мы допустим, что поступательное движение оказывает такое же воздействие на массы всех частиц, как и на электромагнитные массы электронов.

(Заседание Академии Наук 23 апреля 1904 г. Напечатано 27 мая 1904 г.).

Источник: Принцип относительности / Сборник работ классиков релятивизма./ Под редакцией В.К. Фредерикса и В.В. Иваненко. ОНТИ. Ленинград 1935 г. – С. 16–48.