9. ГОРДИЕВ УЗЕЛ РАЗРУБЛЕН
Однажды утром люди обычным жестом развернули газету. Люди были дома, на улицах, за столиками, унылых утром, пивных, за пыльными окнами торговых контор. Глаза, занятые, как всегда, кусочками сахара в стаканах теплого чая, скользнули зевая по строчкам и удивленно прочли:
СЕАНСЫ АВТОМАТА ПРЕКРАЩАЮТСЯ
Билеты взятые на дальнейшие дни аннулируются.
Деньги выдаются в кассе Малого Зала Консерватории и во всех кассах Метрополя от 11–2 часов ежедневно.
Люди недоумевали. Как? Почему? Неужели, победив чемпионов мира, механический рыцарь удаляется на покой? Не может быть! Утка. Чушь.
В редакциях — землетрясение. Звонки телефонов. Ремингтоны и Ундервуды. Репортеры за репортерами отправляются в бой. Редактора благословляют на интервью. Со щитом иль на щите.
К вечеру вторая сенсация. Она поражает прежде всего репортеров. Редакторы от нетерпения и злости рвут гранки очередного набора.
Профессор Ястребов болен и никого не принимает.
Скорей к телефону. Алло. Алло. Алло… Станция… Будьте добры…
Звонок за звонком. Продолжительно. Проверочный стол. Опять барышня… Ах…
— Телефон испорчен, не работает.
Репортеры бегут на Никитскую. Опять и опять. Швейцар устает сообщать — профессор не принимает, нет, никак невозможно. Уговоры мрачного вида прислуги. Не помогает. Потный от волнения гражданин Нахимсон горестно сообщает:
— Болен, в самом деле болен. Ничего не могу поделать. Сам ничего не понимаю…
В Метрополе на всех языках бежит по залу ошеломляющая весть. Маэстро удивлены. 39 иностранных репортеров лихорадочно вытаскивают блок-ноты. Скрипят вечные перья.
Через 10 минут во все 39 газет помчатся умопомрачительные сенсации.
Втихомолку по углам обсуждаются новости. Маэстро втайне довольны. Но любопытство задето. Оно растет и наполняет мозг до краев. Турнир откладывается. Ласкер и Капабланка отказались играть. Пусть сначала выяснятся подробности. А там посмотрим…
Люди по окончании занятий торопливо бегут домой, чтобы вечером у себя, в клубе, в домкоме, в гостях — обсудить, подумать, поахать.
Сон ускользает от глаз. Скользят в полумраке спален черные и белые стаунтоновские фигурки и серое тело металлического чудовища. Лицо профессора Ястребова из диафрагмы обоев появляется крупным планом.
На утро — еще сенсация. Она уже не ошеломляет, а бьет, останавливает дыхание и подгибает колени.
Всего маленькая заметка. Но она разрастается в умах в кошмар, не находящий объяснений. Четыре строчки сухой хроники и в результате — паника, растерянность, ужас.
Вчера, в 11 часов вечера, внезапно скончался профессор Московского университета М. И. Ястребов. Покойный страдал сильно развитым аневризмом и врачи давно уже высказывали возможность смертельного исхода.
Паника. Паника. Паника.
Репортеры в трансе. Погоня за сенсацией внезапной смерти превращается в жизненную проблему. От редакции к редакции. Хрип телефонов. Запросы в Академию Наук. Бешеная скачка в университете.
Бумаги, скорей бумаги. Хотя бы клочки документов. „Вечерка“ платит по полтиннику строчку. Короли газетной хроники соперничают со скоростью автомобильных пробегов.
Тщетно.
Последняя новость глушит, раздирает умы. Догадки разбиваются о скалу непроницаемой тайны. У репортеров — боль под ложечкой и тяжесть у сердца.
Тщетно.
Сенсация кричит, останавливает, давит черным глухим кошмаром.
Бумаг нет. Документы уничтожены. Автомат разбит и разрушен.
Какой-нибудь след! Может быть целы клочки чертежей, формулы?…
Нет! Нет ничего. Разбитые части машины лежат на полу грудой бесполезного никкеля и железа.
Люди успокаиваются. Ничего не поделаешь. Над миром повисла еще одна неразрешенная тайна. Гордиев узел, завязанный профессором Ястребовым, никто не в силах распутать…
День сенсаций. Редактора воспрянули духом. Люди облегченно вздыхают. Наконец-то!
Глаза жадно впиваются в строчки. Буквы танцуют от удовольствия. Типографская краска расплывается от счастья.
Гордиев узел разрублен.
„Редакция „Известий“ получила письмо сотрудника М. Г. У., М. Нахимсона, сына небезызвестного администратора сеансов шахматного автомата. Сам гр. Нахимсон оказался совсем не в курсе изобретения проф. Ястребова. И кроме того, что уже стало всем известно, после смерти профессора, ничего нового сообщить не мог. Отсутствие же документов, уничтоженных изобретателем, лишало всякой возможности отыскать какие-либо научные следы нашумевшего открытия.
Поэтому, считая, что письмо это является первым и единственным фактором, проливающим некоторый свет на сущность системы проф. Ястребова, редакция помещает его целиком:
„Уважаемый товарищ редактор.
„Ввиду того, что я в настоящее время оказываюсь единственным человеком, обладающим хотя и не в полной мере тайной открытия покойного профессора М. И. Ястребова, считаю себя обязанным поставить в известность о ней всех интересующихся этим вопросом.
„С профессором я был знаком еще по университету, где, как известно, он читал специальный курс дифференциального и интегрального исчисления. В последнее время я часто встречал его у отца, от которого и узнал о предстоящей демонстрации шахматного автомата.
„Будучи математиком и немножко шахматистом, я, естественно, заинтересовался и сущностью системы профессора и принципами конструкции его механизма. После долгих моих просьб и упорного нежелания М. И. объяснить мне, на основании каких законов и предпосылок был создан этот удивительный механизм, профессор, взяв с меня слово, что это останется тайной, победил, наконец, свою недоверчивость.
„Его теория в принципе оказалась очень проста. И передать ее здесь не представляет больших затруднений. Поэтому, полагая, что вопрос этот интересует сейчас немало умов, я постараюсь не упустить ни одной детали.
„Сначала немножко истории.
„Профессор в молодости увлекался египтологией. Участвуя в экспедиции на раскопках близ Хемпдена в Египте, он нашел чрезвычайно любопытный документ, отнесенный им приблизительно к эпохе царствования Амнериса II. Документ представлял собой свиток папируса, на котором была изображена шахматная доска, с довольно примитивными начертаниями фигур и группами различных цифр и знаков.
„Над расшифровкой этого документа профессор проработал около пяти лет. В конце концов ему удалось установить, что это была своеобразная теория шахматной игры, устанавливающая определенные математические законы для ее комбинаций.
„По теории авторов документа, каждая фигура и каждая клетка обозначалась определенными, постоянными цифрами. Комбинация этих цифр, точно вычисленная и проверенная, давала, по их мнению, всегда нужный ход и нужную вариацию.
„В результате упорной работы над разработкой и проверкой этих примитивных, по существу, принципов профессор установил ясную и точную систему.
„Вот приблизительно ее сущность:
„На каждый ход всегда имеется только один ответ. Никаких других ответов быть не может, так как одинаковая значимость их — всегда только кажущаяся, и все они, кроме одного, в результате всегда ошибочны.
Человеческий мозг не в силах с математической точностью за десять — двадцать — тридцать и более ходов рассчитать правильность своего ответа, поэтому ошибки всегда неизбежны. Делающий наименьшее число их обычно выигрывает.
„Правильные ходы в игре встречаются очень часто, так как современные изыскания шахматных теоретиков путем ряда проверок установили для многих положений безошибочные ходы. Но, принимая во внимание огромное число шахматных комбинаций (первый ход дает их уже четыреста, а для вычисления числа комбинаций, получаемых со второго хода, потребуется применение высшей математики), ясно, что число правильных, безошибочных ходов, даже самых первоклассных маэстро всегда ограниченно.
„Поэтому, при абсолютно правильной игре белых, делающие так или иначе какие-то ошибки черные всегда проигрывают. При абсолютно верной игре черных все-таки выигрывают белые, если они делают первый ход. Вот почему автомат всегда играл только белыми.
„Но как можно было установить этот, для любого случая и любой комбинации, нужный ход? Применяя цифровые обозначения фигур и клеток на имеющемся у него документе, профессору удалось составить определенную формулу, при которой всегда при любом положении можно было найти этот безошибочный ход.
„При составлении формулы М. И. Ястребов руководился следующими факторами:
1. X — нужный ход.
2. Цифра фигуры, обозначаемая a, a1, a2, a3, и т. д. до 16.
3. Цифра клетки, обозначаемая b, b1, b2, b3, и т. д. до 64.
4. Отношение между цифрами каждой фигуры, обозначаемое — a/a1=c.
5. Отношение между цифрами каждой клетки, обозначаемое b/b1=d.
6. Отношение между цифрами фигур и клеток, обозначаемое a/b=e.
„Кроме того, один определенный коэффициент 1,23 и некоторые постоянные величины, обозначаемые им α, β, γ.
„Обозначая суммы цифр и клеток и отношений между ними через прописные, получаем:
Σa=A, Σb=B, Σc=C, Σd=D, и Σe=E.
„Таким образом, применяя эти обозначения профессора, мы имеем следующую формулу:
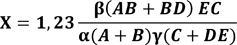
„Подставляя в эту формулу цифровые значения, мы всегда получаем дробь, в которой числитель является цифрой фигуры, а знаменатель цифрой клетки.
„Но вот здесь и исчерпываются сведения о сущности системы профессора. Цифровых значений фигур и клеток он мне не открыл, и они были сожжены им вместе с чертежами автомата. Если кто-нибудь когда-нибудь сумеет установить эти цифры (из которых, если не ошибаюсь, как приведенный профессором пример, ферзь значил — 73), то, применяя формулу М. И. Ястребова, всегда сумеет проверить его математические обоснования и выводы.
„Теперь о конструкции механизма. О ней немного. Могу сообщить только, что это была сложная система арифмометров, позволяющих вычислить все производные в любой момент игры, при любом ее положении. Эти арифмометры управлялись двумя специальными клавиатурами, с обозначением цифр и наименований фигур и клеток. В сложной системе рычагов я признаться мало понял и разобрался, да и интересовала-то меня главным образом сама система, а не ее осуществление.
„Вот все, что я знаю, и все, что мог, я изложил в том же приблизительном плане, как передал мне покойный М. И. Ястребов“.
В академии, в университетах, в математических и технических институтах статья не произвела фурора. В своем стремительном беге вперед, в будущее, наука не видела маленьких королей и ферзей и маленькие, смешные законы их скромных владений.
Но шахматисты облегченно вздохнули. Шахматы спасены. Искусство не стало жертвой математической гильотины.
И жизнь их снова покатилась спокойно и гладко.
Назад: 8. ТРАГЕДИЯ ПРОФЕССОРА ЯСТРЕБОВА
На главную: Предисловие






