Уайлс сознавал, что, дав математике одно из величайших доказательств, он лишил ее одной из величайших загадок: «Люди говорили мне, что я отнял у них проблему, и просили дать им взамен что-нибудь еще. Математики впали в меланхолию. Мы утратили нечто такое, что было с нами на протяжении долгого времени и что многих из нас привлекло к математике. С математическими проблемами всегда так. Нам всегда необходимо находить новые проблемы, которые привлекли бы наше внимание».

Но хотя Уайлс действительно разгадал самую знаменитую математическую проблему, любителям трудных задач-головоломок не стоит терять надежду. Нерешенных проблем еще осталось превеликое множество. Многие из них, как и Великая теорема Ферма, уходят корнями в древнегреческую математику, понять их может любой школьник. Например, множество загадок и поныне связано с простыми числами. В главе 1 мы уже упоминали о том, что совершенным называется число, сумма делителей которого совпадает с самим числом. Например, 6 и 28 — совершенные числа, так как

1, 2, 3 делят 6, и 6 = 1 + 2 + 3,

1, 2, 4, 7, 14 делят 28, и 28 = 1 + 2 + 4 + 7 + 14.

Рене Декарт говорил, что «совершенные числа, подобно совершенным людям, встречаются весьма редко». Самое большое из известных совершенных чисел содержит в своей десятичной записи 130000 цифр и определяется по формуле

2²¹⁶⁰⁹⁰·(2²¹⁶⁰⁹¹ — 1).

Общее свойство всех известных совершенных чисел заключается в том, что они четны. Поэтому так и подмывает сказать, что все совершенные числа четны. Проблема, увы, пока не поддающаяся решению, заключается в том, чтобы доказать это утверждение.

Другая сложная проблема, связанная с совершенными числами, состоит в выяснении ответа на вопрос, можно ли исчерпать запас совершенных чисел за конечное число шагов. На протяжении веков многие математики, занимающиеся теорией чисел, пытались выяснить, конечно или бесконечно множество совершенных чисел, но всякий раз терпели неудачу. Всякому, кому удалось бы дать определенный ответ на этот вопрос, уготовано почетное место в истории математики.

Еще одна область богата древнейшими нерешенными проблемами — теория простых чисел. Последовательность простых чисел подчиняется какой-то плохо различимой закономерности, и простые числа живут по собственным правилам. Их сравнивают с сорной травой, случайным образом распределенной среди натуральных чисел. Перебирая одно за другим натуральные числа, можно набрести на области, богатые простыми числами, но, по неизвестной причине, другие области оказываются совершенно пустыми. Математики веками пытались разгадать закон, по которому распределены простые числа, и всякий раз терпели поражение. Возможно, никакого закона не существует, и распределение простых чисел случайно по самой своей природе. В этом случае математикам можно было бы порекомендовать заняться решением менее амбициозных проблем, связанных с простыми числами.

Например, две тысячи лет назад Евклид доказал, что запас простых чисел неисчерпаем (см. гл. 2). Последние два столетия математики пытались доказать, что запас простых чисел-близнецов также неисчерпаем. Близнецами называют пары простых чисел, отличающихся на 2, т. е. являющихся ближайшими соседними простыми числами (простые числа не могут отличаться на 1, иначе одно из них должно было бы быть четным). Примерами небольших простых чисел-близнецов могут служить (5, 7), (11, 13) и (17, 19), примерами больших чисел-близнецов — (22271, 22273) и (1 000 000 000 061, 1 000 000 000 063). Существуют веские основания полагать, что множество простых чисел-близнецов бесконечно, но никому пока не удалось доказать, что это действительно так.

Самый большой прорыв к доказательству так называемой гипотезы простых чисел произошел в 1966 году, когда китайскому математику Чену Джинграну удалось показать, что существует бесконечное множество пар простых и почти простых чисел. У настоящих простых чисел нет делителей (отличных от самого числа и единицы), а почти простые числа уступают простым самую малость: у них существуют только два простых делителя. Например, число 17 простое, а число 21 (=3·7) — почти простое. Что же касается таких чисел, как 120 (=2·3·4·5), то они не простые и не почти простые, так как их можно представить в виде произведения нескольких простых множителей. Чен доказал, что существует бесконечно много случаев, когда простое число имеет в качестве близнеца либо другое простое число, либо почти простое число. Тот, кому удастся продвинуться еще на один шаг и снять оговорку «почти», совершит величайший прорыв в теории простых чисел со времен Евклида.

Еще одна загадка простых чисел восходит к 1742 году, когда Христиан Гольдбах, учитель малолетнего царя Петра I, написал письмо великому математику Леонарду Эйлеру (который был родом из Швейцарии, но почти всю жизнь проработал в Петербурге). Рассмотрев десятки четных чисел, Гольдбах заметил, что все они представимы в виде суммы двух простых чисел:

4 = 2 + 2,

6 = 3 + 3,

8 = 3 + 5,

10 = 5 + 5,

50 = 19 + 31,

100 = 47 + 53,

21000 = 17 + 20983,

. . . . . .

Гольдбах спрашивал у Эйлера, может ли тот доказать, что каждое четное число представимо в виде суммы двух простых чисел. Несмотря на многолетние усилия, Эйлеру, которого считали «живым воплощением анализа», так и не удалось решить проблему Гольдбаха. Ныне, в век компьютеров, гипотезу Гольдбаха подвергли проверке. Оказалось, что она верна для любого четного числа до 100 000 000, но доказать, что она верна для любого из бесконечно многих четных чисел, пока никому не удалось. Математики сумели доказать, что любое четное число представимо в виде суммы не более, чем 800 000 простых чисел, но этот результат весьма далек от доказательства первоначальной гипотезы Гольдбаха. Но даже столь слабые результаты позволили пролить свет на природу простых чисел, и в 1941 году российскому математику Ивану Матвеевичу Виноградову, которому удалось продвинуться на пути к доказательству гипотезы Гольдбаха, была присуждена Сталинская премия в размере 100 000 рублей.

Из всех проблем, способных с большей или меньшей вероятностью занять место Великой теоремы Ферма, наибольшие шансы имеет проблема плотнейшей упаковки шаров Кеплера. В 1609 году немецкий ученый Иоганн Кеплер доказал, что планеты движутся не по круговым, а по эллиптическим орбитам. Это открытие совершило переворот в астрономии и позднее помогло Исааку Ньютону найти закон всемирного тяготения. Математическое наследие Кеплера не столь грандиозно по своим масштабам, как наследие Ньютона, но не менее глубоко. Проблему плотнейшей упаковки шаров можно сформулировать как задачу о том, как наиболее экономно сложить из апельсинов пирамиду.

Проблема родилась в 1611 году, когда Кеплер написал небольшое сочинение «О шестиугольных снежинках», предназначенное в дар его покровителю Иоганну Вакгеру фон Вакенфельсу. В этом сочинении Кеплер успешно объяснил, почему снежинки всегда имеют шестиугольную форму, высказав предположение, что рост каждой снежинки начинается с обладающего гексагональной симметрией зародыша, который, падая в атмосфере, увеличивается в размерах. Непрерывно изменяющиеся ветер, температура и влажность позволяют каждой снежинке сохранять индивидуальность, а малые размеры зародыша приводят к тому, что условия, от которых зависит его рост, остаются одинаковыми со всех шести сторон, тем самым способствуя сохранению симметрии. В этом, на первый взгляд легкомысленном, сочинении проявился присущий Кеплеру замечательный талант извлекать глубокие и далеко идущие результаты из простейших наблюдений. Впоследствии Кеплер стал одним из основоположников кристаллографии.

Интерес Кеплера к расположению и самоорганизации частиц вещества привел его к обсуждению другого вопроса — о плотнейшей упаковке частиц, при которой они занимают наименьший объем. Если предположить, что частицы имеют форму шаров, то ясно, что как бы они ни располагались в пространстве, между ними неизбежно останутся зазоры, и вопрос состоит в том, чтобы объем зазоров свести к минимуму. Кеплер рассмотрел несколько различных вариантов расположения шаров и для каждого варианта вычислил коэффициент заполнения пространства.

Один из первых вариантов расположения шаров, рассмотренных Кеплером, сейчас принято называть гранецентрированной кубической решеткой. Ее можно построить, выложив сначала нижний слой шаров так, чтобы каждый шар был окружен шестью другими шарами. Второй слой образуют шары, уложенные в «ямки» поверх первого слоя, как показано на рис. 24. По существу, второй слой повторяет первый, но только слегка смещен относительно первого, чтобы шары второго слоя расположились в ямках первого слоя. Именно так обычно укладывают апельсины торговцы фруктами. Коэффициент заполнения пространства такой укладки составляет 74 %. Это означает, что при укладке апельсинов в картонный ящик гранецентрированная стратегия позволяет заполнить 74 % объема ящика апельсинами.

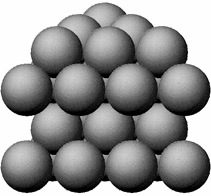
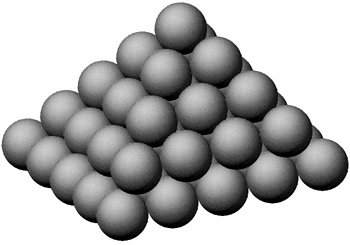
 Рис. 24. В гранецентрированной кубической упаковке шаров каждый слой состоит из сфер уложенных так, что каждая из них окружены шестью другими сферами. Поверх каждого слоя горизонтально накладывается следующий слой так, что любой из его шаров располагается не на шаре из предыдущего слоя, а в ямке. Частной разновидностью гранецентрированной кубической упаковки служат пирамиды из апельсинов в витринах овощных магазинов

Гранецентрированную кубическую решетку можно сравнить с другими вариантами упаковки, например, с простой кубической решеткой. В этом случае каждый слой состоит из шаров, расположенных в виде квадратной решетки, а каждый следующий слой расположен в точности поверх предыдущего, как показано на рис. 25. Простая кубическая решетка имеет коэффициент заполнения пространства 53 %.

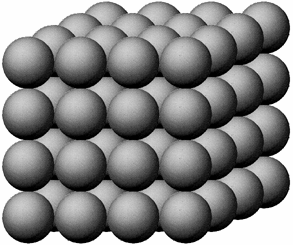
 Рис. 25. В простой кубической упаковке каждый слой состоит из шаров расположенных в виде квадратной решетки. Поверх каждого слоя горизонтально накладывается следующий слой так, что каждый его шар располагается строго над шаром предыдущего слоя

Еще один вариант расположения шаров — гексагональная решетка — аналогичен гранецентрированной кубической решетке, поскольку каждый слой состоит из шаров, окруженных шестью другими шарами, но следующий слой не сдвинут относительно предыдущего, а расположен прямо поверх него так, что каждый шар опирается на самую верхнюю точку шара, расположенного под ним, как показано на рис. 26. У гексагональной решетки коэффициент заполнения пространства составляет всего лишь 60 %.

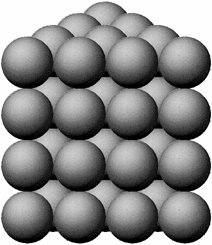
 Рис. 26. В упаковке с гексагональной решеткой каждый слой состоит из шаров расположенных так, что каждый из них окружен шестью другими шарами. Поверх каждого слоя горизонтально накладывается следующий слой так, что каждый шар верхнего слоя располагается непосредственно над шаром предыдущего слоя

Кеплер исследовал множество различных конфигураций и пришел к заключению, что в сочинение «О шестиугольных снежинках» стоит включить только одну, а именно ту, которая в последствие получила название гранецентрированной кубической решетки, ибо у нее «упаковка оказывается плотнейшей из возможных». Утверждение Кеплера можно считать вполне разумным, так как коэффициент заполнения пространства для гранецентрированной кубической решетки наибольший из всех тех, которые были им обнаружены. Однако это не исключает возможность существования какого-то другого расположения шаров, с еще большим коэффициентом заполнения пространства, которое Кеплер попросту проглядел.

Проблема плотнейшей упаковки шаров требует от математиков доказательства того, что гранецентрированная кубическая решетка представляет собой наиболее эффективный вариант упаковки шаров. Эта проблема на полвека старше Великой теоремы Ферма и, как теперь оказалось, еще более неприступна.

Как и в случае Великой теоремы Ферма, решение проблемы Кеплера сводится к доказательству, охватывающему бесконечное множество возможных вариантов упаковки. Гипотеза Кеплера утверждает, что среди бесконечно многих вариантов расположения шаров нет ни одного такого, у которого коэффициент заполнения пространства был бы больше, чем у гранецентрированной кубической решетки. Математикам предстоит доказать, что это невозможно не только для регулярного, но и для случайного, хаотического, варианта расположения шаров.

За последние 380 лет никому не удалось доказать, что гранецентрированная кубическая решетка действительно служит оптимальной стратегией упаковки. Но никто пока не открыл более эффективного метода упаковки. Отсутствие контрпримера означает, что для всех практических целей утверждение Кеплера применимо, но в абсолютном мире математики абсолютно необходимо строгое доказательство. Британский специалист по упаковке шаров К. А. Роджерс говорит, что «большинство математиков в правильность гипотезы Кеплера верят, а все физики в ее правильности твердо убеждены, так как это знают».

Несмотря на отсутствие полного доказательства, за прошедшие со времен Кеплера столетия было пройдено несколько вех на пути к решению. В 1892 году скандинавский математик Аксель Туэ нашел доказательство для двумерного аналога проблемы Кеплера, т. е. обнаружил наиболее эффективное расположение шаров в одном-единственном слое, или, иначе говоря, укладки апельсинов не в ящике, а на подносе. Решением оказалось гексагональное расположение шаров. Впоследствие Тот, Сегрэ и Малер пришли к тому же заключению, но ни один из использованных в двумерном случае методов не применим к исходной трехмерной проблеме Кеплера.

В наше время некоторые математики попытались подойти к проблеме Кеплера с совершенно другой стороны, а именно — вычислить верхний предел коэффициента заполнения пространства. В 1958 году К. А. Роджерс вычислил его верхний предел, который оказался равным 77,97 %. Это означает, что невозможно расположить шары так, чтобы коэффициент заполнения пространства был выше 77,97 %. Такое значение коэффициента заполнения пространства не намного больше, чем его значение для гранецентрированной кубической решетки, равное 74,04 %. Следовательно, если у какого-нибудь расположения шаров коэффициент заполнения пространства и оказался бы выше, чем у гранецентрированной кубической решетки, то превышение составило бы всего лишь несколько процентов. Оставалось узкое окно в 3,93 %, в которое могло бы «втиснуться» какое-то дикое расположение шаров, которое стало бы контрпримером, опровергающим гипотезу Кеплера. После Роджерса другие математики попытались полностью закрыть образовавшееся окно, понизив верхний предел до 74,04 %. Если бы эти попытки оказались удачными, то для других расположений не осталось бы места, они не могли бы иметь более высокий коэффициент заполнения пространства, чем гранецентрированная кубическая решетка, и тем самым гипотеза Кеплера оказалась бы «оправданной ввиду неявки подозреваемой». К сожалению, снижение верхнего предела оказалось процессом медленным и трудным, и к 1988 году верхний предел удалось уменьшить лишь до 77,84 %, что лишь незначительно улучшает оценку Роджерса.

Несмотря на столь медленный прогресс, проблема плотнейшей упаковки шаров летом 1990 года неожиданно попала в заголовки на первых полосах газет. Ву-И Хзянь из Калифорнийского университета в Беркли опубликовал результат, который, по его утверждению, был доказательством гипотезы Кеплера. Первоначально реакция математического сообщества была оптимистической, но когда работа Ву-И Хзяня подверглась тщательному рецензированию, в ней был обнаружен ряд ошибок, и доказательство рухнуло.

Как и в случае с доказательством Уайлса, Хзянь через год представил пересмотренный вариант доказательства, в котором, как он утверждал, ему удалось обойти те проблемы, которые были обнаружены в первоначальном варианте рукописи. К сожалению для Хзяня, его критики продолжали считать, что в его логике остаются пробелы. В письме к Хзяню математик Томас Хейлис попытался объяснить свои сомнения: «Одно предположение, сделанное в Вашей второй статье, представляется мне более фундаментальным и не менее трудным для доказательства, чем остальные… Ваши рассуждения весьма основательно и по существу опираются на это предположение, однако нигде нет и намека на его доказательство».

С тех пор, как Хзянь представил усовершенствованный вариант доказательства, между ним и его критиками шла непрекращающаяся борьба. Правильность предъявленного Хзянем усовершенствованного доказательства остается под вопросом. Во всяком случае, для того, кто хочет доказать гипотезу Кеплера, дверь остается открытой. В 1996 году Дуг Мудер изложил свое ви́дение ситуации вокруг доказательства Хзяня, обнаружив некую интригу:

«Недавно я вернулся с Совместной летней научно-исследовательской конференции по дискретной и вычислительной геометрии, состоявшейся в Маунт Холиоке под эгидой Американского математического общества, Института управленческих наук и Общества промышленной и прикладной математики. Такие конференции проводятся раз в десять лет, поэтому акцент делался на прогрессе, достигнутом за последние десять лет. Хзянь заявил о том, что ему удалось доказать гипотезу Кеплера шесть лет назад. Я обнаружил, что сообщество пришло к согласию по этому поводу: его доказательство "никто не покупает".

На пленарных лекциях и во время неформальных дискуссий неоднократно обсуждались следующие вопросы.

1. В статье Хзяня (опубликованной в "International Journal of Mathematics" в 1993 году) не содержится доказательства гипотезы Кеплера. В лучшем случае это набросок доказательства (на 100 страниц!), его общий ход. Таким доказательство могло бы быть.

2. Эта статья не может считаться даже наброском, так как к некоторым ее утверждениям обнаружены контрпримеры.

3. Столь же необосновано утверждение Хзяня о якобы найденном им доказательстве гипотезы о додекаэдре (и различных других ранее недоказуемых проблем упаковки шаров).

4. Работа над гипотезой Кеплера и гипотезой о додекаэдре должна продолжаться так, как если бы статьи Хзяня никогда не существовали.

В одной из лекций Габор Фейеш-Тот из венгерской Академии наук так отозвался о статье Хзяня: "Эту работу нельзя рассматривать как доказательство. Проблема по-прежнему остается открытой." Ему вторил Томас Хейлис из Мичиганского университета: "Проблема Кеплера остается нерешенной. Я не решил ее. Хзянь не решил ее. Насколько мне известно, никто не решил ее." (Хейлис предсказывал, что его собственный метод позволит решить проблему Кеплера "через год-другой".)

Самое интересное в этой истории — то, что один математик так и не присоединился к общему мнению, а именно сам Хзянь (он не был участником конференции). Хзянь был великолепно осведомлен о контрпримерах и о том, что специалисты не верят его утверждениям, но продолжал выступать с лекциями по всему миру, в которых не уставал снова повторять эти утверждения. Те математики, которым доводилось лично общаться с Хзянем (например, Хейлис и Бездек), считают, что Хзянь никогда не признавал, что в его статье имеются ошибки.

Именно по этой причине «пыль» оседала так медленно. Хзянь впервые заявил о том, что располагает доказательством гипотезы Кеплера в 1990 году, т. е. шесть лет назад. Публичные выступления Хзяня достаточно расплывчаты и неопределенны для того, чтобы быть правдоподобными. Через несколько месяцев после первых заявлений о том, что он располагает доказательством, когда появился первый препринт, в доказательстве сразу же были обнаружены пробелы, а вскоре последовали и контрпримеры. Но Хзянь упорно не прекращал лекционную деятельность, и это обстоятельство создавало впечатление, что он, по-видимому, справляется с теми возражениями, которые возникают. Объем его статьи и то, что текст доказательства претерпел несколько переработок до публикации, еще больше усиливали разноголосицу и неразбериху.

Случай с Хзянем показывает, до какой степени математики полагаются на представления о чести. Математическое сообщество исходит из предположения, что почтенные профессора из самых престижных университетов не станут делать скоропалительные, безосновательные заявления и откажутся от ошибочных утверждений, едва в них будет обнаружен пробел. Тот, кто нарушит сложившуюся систему, основанную на представлениях о профессиональной честности, породит смятение, которое будет длиться долго, так как ни у кого нет ни желания, ни времени следовать повсюду за нарушителем и опровергать его всякий раз, когда он будет высказывать ложные утверждения. (Представьте себе, какой объем работы потребовалось проделать Хейлису, чтобы написать свою разоблачительную статью, опубликованную в 1993 году на страницах журнала "Mathematical Intelligencer", и примите во внимание, что она ничего не дала для математической карьеры самого Хейлиса, — и вы поймете эту проблему. Хзянь опубликовал ответ на статью Хейлиса, но его доводы оказались совершенно несостоятельными. Хейлис счел, что критика ответа Хзяня означала бы вхождение в нескончаемый цикл, на продолжение которого у него просто нет времени.)

Хзянь мог позволить себе не признавать своих ошибок, но как обстояло с редколлегией "International Journal"? Ясно, что члены редколлегии оказались вовлеченными в процесс, который пошел не так, как предполагалось. Статья Хзяня не была прорецензирована должным образом, если вообще была прорецензирована. Ранее «Journal» не проявлял ни малейшего интереса к проблеме плотнейшей упаковки шаров. Было ясно, что Хзянь остановил свой выбор на "International Journal" не потому, что это было подходящее периодическое издание для публикации его статьи, а потому, что этот журнал издавали его друзья.

Кароль Бездек, который больше года работал в контакте с Хзянем, пытался заполнить пробелы в его доказательстве, и представил в «Journal» статью, содержащую контрпример одной из лемм Хзяня. Публикация статьи Бездека затянулась надолго — с декабря. Столь долгий срок бывает иногда необходим для рецензирования статьи, но не совсем обычен для контрпримера к самой разрекламированной статье, опубликованной в «Journal» за многие годы».