Теоретическая физика высоких энергий в 1960-х годах оперировала весьма необычной идеологией. В чём-то эта идеология созвучна идеям физиолога Б. Ф. Скиннера, гуру бихевиоризма, утверждавшего, что только внешнее поведение человека может служить объективным материалом для изучения человеческого мышления. Согласно Скиннеру, физиолог не должен иметь дела с внутренним психическим состоянием человека. Он зашёл настолько далеко, что утверждал, будто такой вещи, как внутренний психологический мир, вообще не существует. Задача физиолога состоит в наблюдении, измерении и фиксации внешнего поведения субъекта без каких бы то ни было попыток судить о его внутренних чувствах, мыслях или эмоциях. Для бихевиориста человек представляет собой чёрный ящик, преобразующий сигналы от органов чувств на входе в поведение на выходе.

Физический бихевиоризм называется теорией S-матрицы. В начале 1960-х, когда я ещё был студентом, многие продвинутые теоретики в Беркли считали, что физики не должны пытаться объяснить внутреннее устройство адронов, а вместо этого рассматривать набор законов адронной физики как чёрный ящик, называемый матрицей рассеяния, или просто S-матрицей. Подобно бихевиористам, защитники S-матрицы требовали, чтобы теоретическая физика строго ограничивалась областью экспериментальных данных и не занималась спекуляциями относительно ненаблюдаемых (как тогда считалось) явлений, будто бы имеющих место на абсурдно малых расстояниях, например внутри протона.

На вход чёрного ящика подавался специфический набор частиц, сталкиваемых друг с другом. Это могли быть протоны, нейтроны, мезоны и даже атомные ядра. Каждая частица характеризовалась импульсом, спином, электрическим зарядом и другими индивидуальными свойствами. Эти частицы исчезали внутри метафорического чёрного ящика, а затем на выходе регистрировался другой набор частиц – результат столкновения, опять же каждая со своими индивидуальными свойствами. Догма Беркли запрещала заглядывать внутрь чёрного ящика в попытке узнать устройство его механизма. Всё, что мы имели, – только исходный и конечный наборы частиц. Этот подход полностью соответствовал тому, чем занимались экспериментаторы на ускорителях, имея пучки высокоэнергетичных частиц на входе и данные детекторов, регистрирующих продукты столкновений, на выходе.

S-матрица – это просто таблица квантово-механических вероятностей. Вы имеете входные данные, а S-матрица сообщает вам вероятности того, что вы можете получить на выходе. Таблица вероятностей зависит от направлений и энергий входящих и выходящих из чёрного ящика частиц, и, согласно превалирующей идеологии середины 1960-х годов, теория элементарных частиц должна быть строго ограничена изучением зависимости S-матрицы от этих переменных. Всё остальное было запрещено. Идеологи решили, что они лучше знают, как лучше для науки, и превратились в стражей научного пуризма. Теория S-матрицы была здоровым напоминанием о том, что физика является эмпирической наукой, но, как и в случае с бихевиористами, философия S-матрицы завела их слишком далеко. По мне, это всё походило на засовывание удивительного цветного мира в серый унылый стерилизатор бухгалтерских таблиц. И я взбунтовался. Но у меня не было подходящей для бунта теории.

В 1968 году молодой итальянский физик Габриэле Венециано жил и работал в Израиле в институте Вейцмана. Он не был идеологически подкован в вопросах теории S-матрицы, но его занимала одна имеющая отношение к S-матрице математическая задача. Существовали определённые технические требования, которым должна удовлетворять S-матрица, но никто до того времени не мог написать ни одного удовлетворяющего этим требованиям математического выражения. Венециано пытался найти хотя бы одно. Его попытка завершилась блестящим успехом. Он получил чрезвычайно аккуратный результат, известный сегодня как «амплитуда Венециано». Но это не было изображением внутреннего строения каких-то частиц или визуализацией процессов столкновения. Амплитуда Венециано была красивым математическим выражением – элегантной математической таблицей вероятностей.

Процесс открытия теории струн, который в определённом смысле все ещё продолжается, изобиловал поворотами судьбы, предательствами фортуны и интуитивными озарениями. Моё собственное участие в нём началось где-то в конце 1968 или в начале 1969 года. Я начал уставать от проблем элементарных частиц; особенно досаждали мне адроны, концепция которых, казалось, мало что может предложить в плане новых глубоких принципов. Я нашёл метод S-матрицы скучным и начинал подумывать о том, чтобы заняться соединением квантовой механики и гравитации. Соединение общей теории относительности с принципами квантовой механики казалось гораздо более интересной задачей, несмотря на то что все имевшиеся экспериментальные данные касались исключительно адронов. Но как раз в это время меня посетил в Нью-Йорке мой израильский друг Гектор Рубинштейн, который был чрезвычайно воодушевлён работой Венециано.

Сначала я не особо заинтересовался. Адроны были тем, о чём я хотел забыть, но из вежливости я согласился выслушать Гектора.

Гектор был настолько возбуждён, объясняя мне идеи итальянца, что я не вполне улавливал детали. Насколько я мог понять, Венециано придумал формулу для описания того, что произойдёт при столкновении двух адронов. Наконец, Гектор записал уравнение Венециано на доске в моем офисе. Это был финальный аккорд. Уравнение оказалось чрезвычайно простым и имело некоторые особенности, показавшиеся мне подозрительно знакомыми. Я, помню, спросил Гектора, не представляет ли это уравнение описание какой-то очень простой квантово-механической системы, потому что оно выглядело так, будто бы имело отношение к гармоническим осцилляторам. Гектор не знал, какая физическая картина могла бы стоять за этим уравнением, поэтому я просто записал его на листке бумаги, чтобы не забыть.

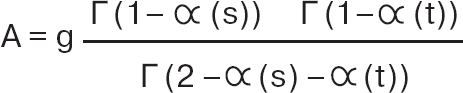
Я был достаточно заинтригован, чтобы отложить размышления о квантовой гравитации и дать адронам ещё один шанс. Как оказалось, мне не суждено было вернуться к гравитации в течение последующих лет. Я несколько месяцев обдумывал это уравнение, прежде чем увидел то, что стояло за ним в действительности.

Термин гармонический осциллятор применяется физиками ко всему, что способно вибрировать, дрожать, колебаться или вообще совершать периодические движения туда-сюда. Ребёнок, качающийся на качелях, и грузик, колеблющийся на пружине, являются примерами типичных гармонических осцилляторов. Вибрирующая скрипичная струна или даже воздух, через который проходит звуковая волна, – это тоже гармонические осцилляторы. Если колеблющаяся система очень мала, например если это атом или молекула, то её поведение определяется законами квантовой механики, и энергия такого осциллятора может изменяться только дискретными порциями. Я упомянул гармонический осциллятор в беседе с Гектором, потому что уравнение Венециано напомнило мне о математических свойствах квантово-механического гармонического осциллятора. Я представил себе адрон в виде двух грузиков, соединённых пружиной, совершающих гармонические колебания, сближаясь и удаляясь. Я играл с запретным плодом, пытаясь изобразить внутреннее устройство элементарной частицы, и отдавал себе в этом отчёт.

Танталовы муки, которые я испытывал от ощущения близости ответа и невозможности его ухватить, сводили меня с ума. Я испробовал все варианты квантово-механических осцилляторов, пытаясь подобрать такой, который вписался бы в уравнение Венециано. Мне удалось написать уравнения, очень похожие на уравнения Венециано, описывающие разные варианты моделей грузиков на пружинках, но все они не годились. В течение этого периода я потратил много часов собственного времени, работая на чердаке своего дома. Возвращаясь оттуда усталым и раздражительным, я ругался с женой и игнорировал детей. Мне не удавалось выкинуть это уравнение из головы даже во время обеда. И вдруг, в один из вечеров, без всякой уважительной причины на меня на чердаке снизошло озарение. Я не знаю, что вызвало к жизни эту мысль: ещё минуту назад я представлял себе пружину и вдруг увидел вместо неё эластичную струну, натянутую между двумя кварками и имеющую много различных мод колебаний. В одно мгновение я понял, что весь трюк состоит в том, чтобы заменить математическую пружину непрерывной натянутой струной. На самом деле слово струна тогда не пришло мне на ум. Я подумал о резиновом кольце. Если разрезать резиновое кольцо, оно превратится в резинку с двумя свободными концами. На каждый из концов я мысленно поместил по кварку, точнее, кварк на один конец и анти-кварк на другой.

Я быстро сделал несколько расчётов в своей записной книжке для проверки идеи, хотя уже знал, что это будет работать. Это было потрясающе просто. Уравнение Венециано для S-матрицы оказалось точным описанием столкновения двух резинок. Почему эта мысль раньше не приходила мне в голову?

Ничто не приносит такую радость, как новые открытия. Это случается нечасто даже у величайших физиков. Вы говорите себе: «Сейчас я – единственный человек на планете, который это знает. Скоро об этом узнает и остальная часть мира, но на данный момент я – единственный». Я был молод и неизвестен и жаждал славы. Но я не был единственным.

Примерно в то же самое время один физик из Чикаго проделал те же самые вычисления. Ёитиро Намбу был намного старше меня и уже давно являлся одним из самых выдающихся физиков в мире. Он родился в Японии и пришёл в Чикагский университет молодым физиком сразу после Второй мировой войны. Намбу был звездой и обладал репутацией человека, способного разглядеть некоторые вещи намного раньше всех остальных. Позже я узнал, что ещё один физик в Дании обдумывал весьма схожие идеи. Я не буду отрицать, что был разочарован, узнав, что я не одинок в своей «резиновой» теории, но мысль о том, что я оказался в одной компании с Великим Намбу, тешила моё самолюбие.

Современная теория струн занимается недостижимой унификацией квантовой механики и гравитации, о которую тщетно физики бились своей коллективной головой на протяжении большей части XX века. Другими словами, это теория о том, что представляет собой мир в сказочно крошечном масштабе планковских размеров – 10^–33 сантиметра. Как я уже рассказал, она началась с гораздо более скромной задачи – описания внутренней структуры адронов. В следующей главе мы увидим, как теория струн переродилась в гораздо более глубокую фундаментальную теорию, но давайте начнём с её более ранней инкарнации.

Адроны являются очень маленькими объектами, они примерно в сто тысяч раз меньше атомов. Диаметр адрона составляет порядка 10^–13 сантиметра. Для того чтобы удержать кварки на таких малых расстояниях, требуются колоссальные силы. Адронные струны – резинки в моём воображении – хотя и микроскопически малы, тем не менее невероятно прочны. Если бы было возможно прикрепить один конец мезона (одного из типов адронов) к автомобилю, а другой к подъёмному крану, то адронная струна, удерживающая кварки в мезоне, легко выдержала бы вес автомобиля. Относительно масштабов, достижимых в сегодняшних экспериментах, адронные струны не слишком малы. Современные ускорители позволяют исследовать материю на в сто, а то и в тысячу раз меньших расстояниях. Просто для сравнения позвольте мне забежать вперёд паровоза и показать, что представляет собой прочность струны в её современной инкарнации. Для того чтобы удерживать частицы на расстоянии порядка планковской длины, струна должна быть примерно в 10⁴⁰ раз сильнее, чем адронная струна. Одна-единственная струна была бы способна выдержать вес всей нашей Галактики, если мы могли бы каким-то образом сумели сосредоточить всю массу Галактики вблизи поверхности Земли.

Все адроны подразделяются на три семейства: барионы, мезоны и глюболы. Наиболее известными адронами являются нуклоны – обычные протоны и нейтроны. Они принадлежат к первому семейству – барионам. Все барионы состоят из трёх кварков. Кварки соединяются друг с другом, как предполагается, тремя струнами на манер боласа гаучо: три струны соединены концами в центре, а к свободным концам прикреплены три кварка. Единственное, что неверно в аналогии с боласом, – это то, что адронные струны, в отличие от верёвок, эластичны, они могут растягиваться подобно идеальной резиновой нити. Но поскольку обычные протоны и нейтроны представляют собой самую низкоэнергетическую конфигурацию «боласа», то их можно рассматривать как три кварка, соединённых очень короткими нерастяжимыми нитями.

Кварки на концах струн могут двигаться множеством способов. Например, «болас» может вращаться вокруг центральной точки, где соединяются концы струн, и в этом случае центробежная сила будет растаскивать кварки в разные стороны. Вращение требует энергии (вспомните E = mc²), а это значит, что вращающийся адрон будет тяжелее невращающегося. На физическом жаргоне частица, обладающая дополнительной внутренней энергией, называется возбуждённой. Кварки могут образовать возбуждённое состояние адрона и не вращаясь. Примером такого состояния могут служить колебательные движения кварков в направлении центра. Вдобавок и сами струны могут вибрировать наподобие гитарных. Все эти движения или, по крайней мере, косвенные свидетельства таких движений регулярно наблюдаются в реальных экспериментах с нуклонами. Барионы действительно ведут себя как эластичный квантовый болас.

Что же означает в данном случае «квантовый»? Квантовая механика подразумевает, что энергия (масса) любой колебательной системы может добавляться или отниматься только неделимыми дискретными порциями. На заре экспериментальной адронной физики исследователи не предполагали, что различные квантовые состояния осциллирующей системы представляют собой один и тот же объект, поэтому они давали каждому энергетическому уровню собственное имя, принимая эти уровни за разные элементарные частицы. Протоны и нейтроны являются барионами с наименьшей внутренней энергией. Более массивные состояния получили замысловатые имена, многие из которых уже ничего не говорят современным молодым физикам, поскольку для них это не более чем возбуждённые состояния нейтрона и протона. Поняв суть, физики навели, наконец, порядок в существовавшем до этого зоопарке частиц.

Следующим у нас идёт мезон – частица, которую я изучал на чердаке моего дома в 1969 году. Мезоны устроены гораздо проще, чем барионы. Каждый мезон состоит из кварка и антикварка, соединённых одной струной. Подобно барионам мезоны обладают вращательными и колебательными квантовыми состояниями. Расчёт, который я сделал тогда на чердаке, описывал основной процесс взаимодействия между двумя мезонами-струнами.

При столкновении двух мезонов может произойти несколько различных событий. Поскольку квантовая механика предсказывает только вероятности событий, невозможно заранее предсказать, по какому пути будет разворачиваться история столкновения. Самым вероятным и самым неинтересным вариантом будет прохождение мезонов друг сквозь друга, несмотря на то что при этом и струны, соединяющие кварки и антикварки, тоже пройдут друг сквозь друга. Но существует другая, более интересная возможность: мезоны могут слиться вместе, образовав новый мезон, в котором кварк и антикварк соединены более длинной струной.

Представьте каждую струну в виде группы танцоров, взявшихся за руки, чтобы образовать цепочку. У танцоров, находящихся на конце цепочки, одна рука свободна, а у танцоров в середине цепочки обе руки заняты. На рисунке изображены две цепочки, летящие друг к другу. Единственный способ, которым они могут провзаимодействовать, состоит в том, что танцор на конце одной цепочки возьмёт за свободную руку танцора на конце другой. После этого обе группы танцоров образуют единую цепочку. В этой конфигурации танцоры качаются друг относительно друга в сложном танце, до тех пор пока где-то в середине цепочки один из танцоров не отпустит руку своего соседа. Тогда цепочка снова распадётся на две независимых цепочки, и они продолжат своё движение в новом направлении, удаляясь друг от друга. Более точное, но менее наглядное описание выглядит так: кварк на конце одной струны соединяется с антикварком на конце другой. При этом кварк и антикварк аннигилируют, как и любые другие частицы и античастицы, оставляя после себя одну более длинную струну с оставшимися кварком и антикварком на концах.

Возникающая в результате слияния двух мезонов струна, как правило, оказывается в возбуждённом состоянии, включающем как вращательные, так и колебательные моды. Но спустя некоторое время струна, подобно цепи танцоров, распадается надвое, образуя на свободных концах кварк и антикварк. В итоге мы имеем процесс, в ходе которого две струны соединяются в одну, которая затем снова распадается надвое.

Задача, которую я решил на чердаке, формулировалась следующим образом: предположим, что два мезона (две струны) до столкновения двигались с заданной энергией во встречных направлениях. Какова квантово-механическая вероятность того, что образовавшаяся после столкновения новая пара мезонов будет разлетаться в некотором заданном направлении? Задача выглядит ужасно сложной, и это просто математическое чудо, что она может быть решена.

Математическая задача описания идеального резинового шнура была решена ещё в начале XIX века. Колеблющуюся струну можно рассматривать как совокупность гармонических осцилляторов – по одному для каждого отдельного типа (моды) колебаний. Гармонический осциллятор – одна из немногих физических систем, которые могут быть полностью проанализированы с помощью очень простой математики уровня средней школы.

Добавить квантово-механическое описание, чтобы превратить струну в квантовый объект, тоже не составляет труда. Все, что необходимо помнить, – это что уровни энергии любой квантово-механической колебательной системы обладают дискретными значениями энергии (см. главу 1). Этих простых соображений достаточно, чтобы понять свойства одной колеблющейся струны, но описание двух взаимодействующих струн гораздо сложнее. Для этого мне пришлось разработать собственные правила с нуля, что сделало возможным локализовать сложное описание только для бесконечно малого времени, в течение которого происходит объединение струн. Как только это произойдёт, две струны снова становятся одной, описываемой простой математикой. Чуть позже струна рвётся, и этот процесс снова требует сложного описания, но опять же лишь для короткого промежутка времени. Таким образом, я сумел с большой точностью описать процесс объединения двух струн и последующего распада получившейся струны. Результат своих математических расчётов я сопоставил с уравнением Венециано, и они согласовались с идеальной точностью.

Барион представляет собой три струны, соединённые «звездой», мезон – одну открытую струну, но что такое глюбол? Начнём с цепочки танцоров. Допустим, танцоры, двигаясь в своём сложном танце, изогнули цепочку так, что два крайних танцора оказались рядом друг с другом. Не понимая, что они принадлежат к одной и той же цепочке, они могут взяться за руки. В результате получается замкнутый круг танцоров без свободных концов. То же самое может произойти и с колеблющимся мезоном. Предположим, что в процессе колебаний и вращений концы мезонной струны случайно оказались друг возле друга. Кварк на одном конце видит антикварк на другом и, не догадываясь, что его коллега принадлежит тому же самому мезону, хватает его, как змея собственный хвост. В результате получается глюбол: замкнутая струна, не имеющая на своих концах кварков. Большинство мезонов и барионов было известно задолго до создания теории струн, но глюболы были предсказаны ею, так сказать, с чистого листа. И если сегодня вы посмотрите на список известных частиц, то глюболы и их массы будут перечислены в нём наряду с барионами и мезонами.

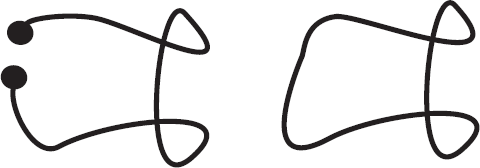
Мезон превращается в глюбол

Глюболы, мезоны и барионы являются сложными объектами, которые могут вращаться и колебаться множеством способов. Например, струна, соединяющая концы мезона, может вибрировать, как пружина или даже как скрипичная струна; он может даже вращаться вокруг своей середины, растягиваясь под действием центробежной силы и образуя своеобразный адронный пропеллер. Эти возбуждённые состояния адронов соответствуют известным объектам, часть которых была обнаружена в экспериментах ещё в 1960-х.

Связь теории адронных струн с Законами Физики, и в частности с их формулировкой в терминах фейнмановских диаграмм, отнюдь не очевидна. Одним из способов визуализации теории струн является генерализация фейнмановских диаграмм путём замены точечных частиц струнами. Фейнмановские диаграммы состоят из основных элементов, которые мы уже рассматривали в главе 1: вершин и пропагаторов. Пропагаторы и вершины хороши для представления бесконечно малых точечных частиц квантовых полей. Например, вершина сама по себе является точкой, в которой сходятся траектории частиц. Если же сами частицы не являются точками, то не совсем понятно, что означает точка встречи их траекторий. Как же придать смысл пропагаторам и вершинам для струн? Когда мы имеем дело с точечной частицей, мы представляем её движение в виде линии в пространстве-времени. В каждый момент времени частица представляется точкой, но в результате движения эта точка разворачивается в кривую линию. Великий Минковский назвал траекторию движения частицы в пространстве-времени мировой линией, и этот термин прочно вошёл в науку.

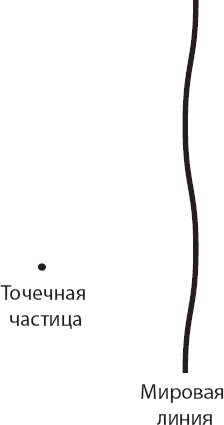
Теперь представим себе, как могла бы выглядеть история струны в пространстве-времени. Возьмём замкнутую струну, не имеющую концов. В каждый конкретный момент времени такая струна будет представляться в пространстве замкнутой кривой. Представьте себе, что эту струну освещает стробоскоп. Во время первой вспышки мы увидим кольцо. При следующей вспышке мы увидим то же самое кольцо, только в другом месте. В конечном итоге мы увидим набор колец, отображающий последовательные положения струны.

Но в действительности время течёт непрерывно, и чтобы составить полную историю движения струны, нужно заполнить промежутки между её последовательными изображениями. В результате получится трубка, проходящая через пространство-время: двумерная цилиндрическая поверхность.

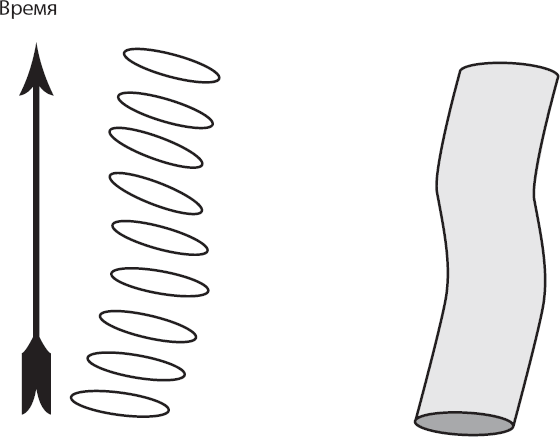
Размер кольца струны может изменяться со временем, ведь струна способна сжиматься, растягиваться и колебаться. Временами она может даже самопересекаться, образуя подобие восьмёрки или принимая более сложные формы. В этом случае цилиндр окажется деформированным, но в нём всё ещё можно будет узнать цилиндр.

Поверхность, заметаемую кольцом, можно было бы очень удачно назвать трубкой мира по аналогии с мировой линией. Но так случилось, что в физике прижился другой термин: мировой лист, или мировая поверхность. Но как бы мы его ни называли, этот цилиндр представляет собой пропагатор струны, который приходит на замену пропагатору точечной частицы.

Мезон, оканчивающийся двумя кварками, тоже может быть представлен в виде мирового листа, только это будет не цилиндр, а лента, имеющая два края. Вернёмся к аналогии со стробоскопом. Теперь мы будем видеть последовательность открытых струн с кварками на концах. Заполнив пространство между последовательными изображениями мезона, мы получим мировой лист в виде ленты.

Но для интересной теории, которая способна была бы описывать сложные взаимодействия сталкивающихся частиц, недостаточно одних только пропагаторов. Нужны ещё вершины, развилки дорог, в которых частицы могли бы излучать и поглощать другие частицы. И теория струн не исключение.

Вершина для открытой струны должна выглядеть как обычная дорожная развилка: в какой-то момент времени струна разрывается посередине, на образовавшихся свободных концах образуются кварк и антикварк, и вот уже две струны продолжают своё путешествие. Закрытые струны тоже могут разделяться на две. Соответствующая этому процессу диаграмма выглядит как Y-образная развилка водопроводной трубы.

Если вы будете следовать по этой диаграмме снизу вверх (от прошлого к будущему), вы увидите, как одна струна расщепляется на две, каждая из которых удаляется в своём направлении. Перевернув диаграмму, вы получите процесс слияния двух струн в одну.

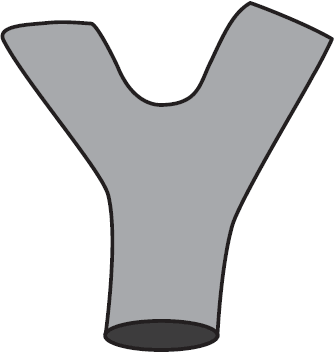
Идея заключается в том, чтобы заменить обычные фейнмановские диаграммы сетью водопроводных труб, представляющих собой пропагаторы струн, и Y-образных развилок, заменяющих прежние вершины. Очень быстро теоретики поняли, что деление диаграммы на цилиндрические пропагаторы и Y-сочленения носит искусственный характер и что в действительности теория содержит мировые листы любой формы и топологии. Диаграммы могут содержать отверстия, представляющие входящие и выходящие струнноподобные глюболы, но в общем случае они могут быть любой сложности.

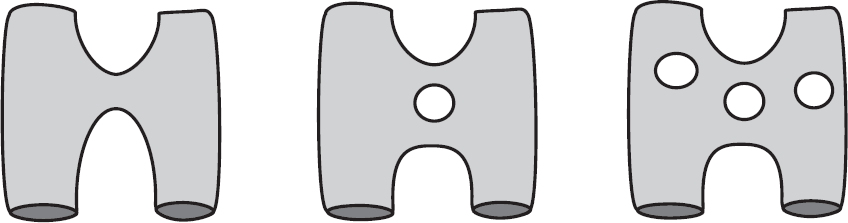
Этот способ представления адронов трудно связать со Стандартной моделью, теорией, основанной на обычных фейнмановских диаграммах, (то есть на точечных частицах). Современная Стандартная модель включает то, что на первый взгляд выглядит как совершенно отличная от всего предыдущего теория адронов – теория, известная под названием квантовая хромодинамика, или КХД.

Согласно КХД, адроны состоят из кварков и антикварков. В этом КХД имеет много общего с теорией струн, которую разрабатывали мы с Намбу. Но удерживающая кварки вместе сила – клей, скрепляющий адроны, – совершенно не похожа на струны. Кварки испускают и поглощают глюоны точно так же, как электроны испускают и поглощают фотоны. Силы, удерживающие кварки в адронах, обязаны своим происхождением обмену глюонами между кварками.

У глюонов есть одна особенность, которая делает их более сложными, чем фотоны. Заряженные частицы могут излучать и поглощать фотоны, но сами фотоны не обладают такой способностью. Другой способ сказать то же самое: не существует вершин, в которых один фотон распадается на два. Глюоны же способны испускать и поглощать другие глюоны.

Существует вершинная диаграмма, на которой три глюона соединяются в одной вершине. В конечном итоге это делает глюоны и кварки гораздо более «липкими», чем электроны и позитроны.

Всё это выглядит так, будто существуют две различные теории адронов: КХД и теория струн. Но, разумеется, почти с самого момента появления теории струн было очевидно, что эти два описания в действительности – лишь два лица одной и той же теории. Просто ключевое Озарение опередило на пару лет открытие КХД.

Мост между обычными фейнмановскими диаграммами и теорией струн показался из тумана, когда в 1970 году я получил письмо от блестящего молодого датского физика Хольгера Бех Нильсена. Он был в восторге от моей статьи, где я излагал теорию с резинкой, и хотел поделиться некоторыми из своих идей. В письме он сообщал, что тоже думал о чём-то, очень похожем на упругую струну, и излагал свои соображения под несколько другим углом.

Идея соединить теорию струн с фейнмановскими партонами была созвучна тому, о чём я сам размышлял в течение продолжительного времени. Нильсен глубоко изучил вопрос и имел собственное, весьма интересное видение проблемы. Он предложил считать, что гладкий непрерывный мировой лист на самом деле представляет собой мелкую сеть из линий и узлов. Другими словами, мировой лист в его представлении был обыкновенной, но чрезвычайно сложной фейнмановской диаграммой, состоящей из огромного числа пропагаторов и вершин. Эта сеть становилась всё более и более гладкой по мере добавления в неё новых вершин и пропагаторов и всё лучше и лучше аппроксимировала гладкий мировой лист. Теория адронных струн тоже может быть сформулирована подобным способом.

Мировые листы, трубки и Y-образные сочленения можно представить как очень сложные фейнмановские диаграммы с участием кварков и огромного количества глюонов. Когда вы смотрите на мировой лист «с большого расстояния», он кажется гладким. Но «под микроскопом» мировой лист выглядит как рыболовная сеть или как баскетбольная корзина, сплетённая из фейнмановских диаграмм. Нити рыболовной сети представляли пропагаторы точечных частиц, узлы – партоны Фейнмана или кварки и глюоны Гелл-Мана, а «ткань», сотканная из этих микроскопических мировых линий, – непрерывный мировой лист.

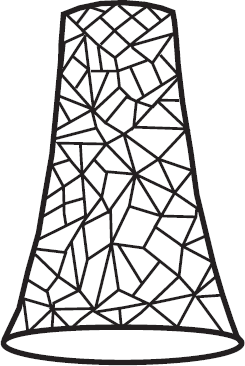
Вы можете представить струну как набор партонов, нанизанных один за другим подобно нитке жемчуга. Фейнмановская партонная теория, Гелл-Мановская кварковая теория и моя «резиновая» теория – всё это различные способы представления квантовой хромодинамики.

Струнной, или «резиновой» модели адронов не сопутствовал немедленный успех. Многие теоретики, занимавшиеся адронной физикой в 1960-х годах, выражали весьма негативное отношение к любой теории, которая пыталась визуализировать явления. Рьяные сторонники теории S-матрицы утверждали, что столкновение – это непознаваемый «чёрный ящик», и отстаивали своё неприятие новой теории с почти миссионерским рвением. Они признавали только одну заповедь – «не срывай покрова», то есть «не заглядывай “внутрь” процесса столкновения, пытаясь обнаружить механизмы происходящих процессов, не пытайся понять строение такой частицы, как протон». Враждебное восприятие идеи о том, что уравнение Венециано описывает столкновение двух резинок, сохранялась до тех пор, пока однажды Мюррей Гелл-Ман не поставил на ней свою печать одобрения.

Мюррей был королём физики, когда я впервые встретился с ним в Корал Гейблс, штат Флорида, в 1970 году. В то время кульминацией сезона теоретической физики была конференция в Корал Гейблс. А кульминацией конференции была лекция Мюррея. Для меня Корал Гейблс оказался первой большой конференцией, на которую я был приглашен не в качестве лектора, а в качестве слушателя. Мюррей начал свою лекцию с темы спонтанного нарушения дилатационной симметрии – одной из проблем, с которой у него были проблемы. Едва ли я смогу вспомнить саму лекцию, но очень хорошо помню, что произошло потом: мы с Мюрреем застряли в лифте.

Я был тогда совершенно неизвестен, в то время как всё физическое сообщество боготворило Мюррея. Разумеется, застряв с ним в лифте, я потерял дар речи.

Чувствуя необходимость как-то начать разговор, Мюррей поинтересовался, чем я занимаюсь. Я испуганно ответил: «Я работаю над теорией адрона, представляющей его как своего рода эластичный шнур, как резинку». В следующий ужасный момент, который я не забуду никогда, он начал смеяться. И это был не короткий смешок, а громогласный гомерический хохот. Я чувствовал себя презренным червём. Затем двери лифта открылись, и я позорно уполз с горящими ушами.

После этого я не встречался с Мюрреем почти два года. Следующая наша встреча состоялась на другой конференции, в Национальной ускорительной лаборатории имени Энрико Ферми, сокращённо Фермилаб. Эта конференция была очень представительной: около тысячи участников, среди которых были наиболее влиятельные теоретики и экспериментаторы со всего мира. И в этот раз я снова был слушателем.

В день открытия конференции, когда мы с группой друзей ожидали начала первой лекции, к нам неторопливо подошёл Мюррей. При всех он сказал: «Мне очень жаль, что я смеялся над вами в лифте в тот день. Я думаю, что задача, над которой вы работаете, – это просто фантастика, и я посвящу ей большую часть моей лекции. Давайте присядем где-нибудь и поговорим об этом, когда у нас выдастся свободная минутка». В этот момент я из червя превратился в принца: сам король оказал мне свою милость!

В течение пары дней после этого, встречая Мюррея, я спрашивал: «Не настало ли время нам поговорить?» И каждый раз он отказывался, ссылаясь на какую-нибудь важную встречу.

В последний день конференции я стоял в длинной очереди к турагенту. Мне нужно было поменять авиабилет, и я ждал своей очереди уже более часа. Наконец, когда передо мной в очереди оставалось только два или три человека, ко мне подошёл Мюррей со словами: «Я свободен! Мы можем поговорить прямо сейчас. У меня есть пятнадцать минут». «О’кей, – сказал я себе. – Это твой шанс. Сделаешь всё правильно, и ты – принц. Сделаешь что-то не так, и ты – наживка для рыбы».

Мы сели за свободный столик, и я начал объяснять, как моя новая «резиновая» теория связана с его и Фейнмана идеями. Я собирался начать с диаграммы рыболовной сети. Помню, я сказал: «Я начну с партонов».

«Партоны? Партоны… Какие, к дьяволу, партоны? Патроны? Пистоны? Вы хотите вставить мне пистон? Так, что ли?» Я понял, что совершил непростительную ошибку, но не мог сообразить какую. Я пытался объяснить, но всё, что я получал в ответ, – это «Патроны? Что это такое?» Так прошли четырнадцать из пятнадцати отведённых мне минут, пока он не спросил: «Патроны – они имеют заряд?» Я ответил: «Да». – «Принадлежат ли они группе SU(3)?» Я снова ответил утвердительно. Тогда его лицо просветлело: «А-а, так вы имеете в виду кварки!» Я совершил смертный грех, назвав составляющие адронов словом, которое придумал Фейнман, а не Мюррей. Похоже, я был единственным физиком на планете, который не подозревал о непримиримом соперничестве между этими двумя титанами из Калтеха.

Во всяком случае, у меня оставались ещё одна или две минуты, за которые я в сжатом виде изложил свои соображения, а затем Мюррей посмотрел на часы и сказал: «Ладно, спасибо. У меня назначена встреча с одним важным человеком, с которым я должен переговорить до моей лекции».

Я был так близко и вместе с тем так далеко. Увы, не для меня королевские почести, а для меня земля и грязь. Но затем я услышал то, что вернуло меня к жизни. Я увидел Мюррея, который пересказывал группе своих коллег всё то, что я успел ему рассказать. «Сасскинд говорит, что… Сасскинд утверждает, что… Мы должны заняться теорией струн Сасскинда…» А затем Мюррей рассказал о моей идее в своём заключительном докладе на конференции. И хотя теории струн была посвящена лишь небольшая часть доклада, она получила благословение Мюррея, а я чувствовал себя как после езды по американским горкам.

Хотя Мюррей не занимался теорией струн, его разум был открыт для новых идей, и Мюррей сыграл важную роль в их продвижении. Нет никаких сомнений, что он был одним из первых, кто признал потенциальное значение теории струн как теории адронов, а позднее и как теории явлений планковских масштабов.

Существует много вариантов теории струн. Наши варианты начала 70-х были математически очень точными – слишком точными. Хотя с современной точки зрения абсолютно ясно, что адроны являются струнами, теория должна была пройти через целый ряд метаморфоз, прежде чем она смогла описать реальные барионы и мезоны.

Имелись три огромные проблемы, досаждавшие первоначальному варианту теории струн. Одна из них была настолько странной, что консерваторы, а особенно энтузиасты S-матриц, нашли в ней источник для шуток. Это была проблема слишком большого количества измерений. Теория струн, как и все физические теории, имеет дело с пространством и временем. До Эйнштейна пространство и время существовали сами по себе, но затем под влиянием Минковского они слились в единое пространство-время – четырёхмерный мир, в котором каждое событие представлено четырьмя координатами: тремя пространственными и одной временной. Эйнштейн и Минковский превратили время в «четвёртое измерение». Но пространство и время не совсем равноправны. Даже в общей теории относительности, которая перемешивает пространство и время путём замысловатых математических преобразований, эти две сущности различаются. Они по-разному «ощущаются». По этой причине, вместо того чтобы говорить о четырёхмерном пространстве, мы обычно говорим о 3 + 1-мерном, обозначая тем самым, что у нас есть три пространственные и одна временная координата.

Может ли пространство иметь большее число измерений? Да, и это обычное явление в современной физике. Не так трудно, как кажется, представить себе движение в пространстве, имеющем более трёх пространственных измерений. Ещё проще представить себе мир, имеющий менее трёх пространственных измерений. Например, в знаменитой книге Эдвина Эббота «Флатландия» описывается жизнь в мире, имеющем только два пространственных измерения. Но ещё никому не удалось представить себе мир, имеющий более (или менее) одного временного измерения. Похоже, что это вообще не имеет смысла. По этой причине физики, оперируя с многомерными пространствами, всегда имеют в виду пространство с 4 + 1, 5 + 1 и т. д. измерениями, подразумевая, что в нём может быть много пространственных, но всегда только одно временное измерение. Физики всегда надеялись, что однажды они сумеют объяснить, почему наш мир имеет именно 3 пространственных измерения, а не 2, 7 или 84. Поэтому струнные теоретики были рады обнаружить, что их математика корректно работает только в определённых количествах измерений. Проблема лишь в том, это количество оказалось равным 9 + 1, а не 3 + 1. Что-то где-то не так с математикой, если количество пространственных измерений, необходимых для её работы, оказывается в три раза большим, чем количество измерений в нашем обычном мире! Это выглядело насмешкой над струнными теоретиками.

Как преподаватель физики я ненавижу рассказывать что-то студентам, а потом заявлять, что я не могу этого объяснить. Это-де слишком сложно или это-де слишком специально. Я трачу массу времени, придумывая, как объяснить сложные вещи простыми словами. Одним из моих самых больших разочарований является то, что мне так и не удалось придумать простого объяснения, почему теория струн может обрести полное счастье только в 9 + 1 измерениях. И никому другому тоже. Всё, что я могу сказать, – это что всё дело в неустранимых квантовых флуктуациях струн. Эти квантовые флуктуации могут накапливаться и полностью выйти из-под контроля, если не будут выполнены определённые, очень тонкие условия. И эти условия выполняются только в пространстве с 9 + 1 измерениями.

Ошибка в три раза – не столь уж большая беда для космологии, но для физики элементарных частиц это просто катастрофа. Физики, изучающие частицы, привыкли к точным числам. И нет другого такого числа, в котором они были бы настолько уверены, как в числе пространственных измерений. Никакая экспериментальная ошибка не способна объяснить потерю шести пространственных координат. Короче, это полное фиаско. Пространство-время и в прошлом, и ныне имело и имеет размерность 3 + 1, и в этом не может быть никаких сомнений.

Провравшись в отношении размерности пространства, теория струн, конечно, поступила очень плохо, но ещё хуже было то, что она провралась и в предсказании закона, которому подчиняются ядерные силы между адронами. Вместо близкодействующих ядерных сил теория предсказывала дальнодействующие силы, неограниченно простирающиеся в пространстве, подобные электромагнитным или гравитационным. Если подогнать короткодействующую ядерную силу под правильное значение, то электрическая сила была бы в 100 раз сильнее, а гравитационная – в 10⁴⁰ раз. О том, чтобы отождествить эти дальнодействующие силы с реальными гравитационными или электрическими силами, не могло быть и речи.

Все силы в мире, будь то гравитационные, электрические или ядерные, имеют одну и ту же природу. Представьте себе электрон, обращающийся вокруг центрального ядра. Время от времени электрон испускает фотоны, и куда же эти фотоны деваются? Если атом возбуждён, то фотон может улететь прочь, а атом перейти на более низкий энергетический уровень. Но если атом уже находится в самом низшем энергетическом состоянии, фотон не может унести с собой часть энергии. Единственный выход для фотона – быть поглощённым другим электроном или положительно заряженным ядром. Таким образом, в реальном атоме электроны и ядра постоянно перебрасываются фотонами подобно цирковым жонглёрам. Этот обмен частицами, в данном случае фотонами, и является источником всех сил в природе. Любые силы – электрические, магнитные, гравитационные – в конечном итоге приводят нас к фейнмановским обменным диаграммам, на которых кванты летают от одних частиц к другим. Для электрических и магнитных сил такими обменными квантами являются фотоны; для гравитационных сил ту же работу выполняют гравитоны. Мы с вами прикованы к Земле гравитонами, которыми обмениваются частицы наших тел с частицами нашей планеты. Но для сил, удерживающих вместе протоны и нейтроны в ядре, такими обменными квантами являются пи-мезоны (пионы). Если заглянуть внутрь протонов и нейтронов, то мы увидим, что составляющие их кварки обмениваются друг с другом глюонами. Установление связи между силами и соответствующими этим силам обменными частицами было одним из величайших достижений физики XX века.

Если природа ядерных, электромагнитных и гравитационных сил одинакова, то отчего же они настолько различны? Электромагнитные и гравитационные силы являются дальнодействующими, что позволяет гравитации удерживать планеты на их орбитах, в то время как ядерные силы сходят на нет уже на расстояниях порядка диаметра протона. Если вы думаете, что различия между силами связаны с какими-то индивидуальными свойствами создающих эти силы обменных частиц, то окажетесь абсолютно правы. Определяющим фактором дальнодействия какой-нибудь силы является масса создающей эту силу обменной частицы: чем легче частица, тем более дальнодействующей является сила. Причина дальнодействия гравитации и электричества состоит в том, что гравитон и фотон являются безмассовыми частицами. А вот пион, наоборот, весьма массивен – его масса в 300 раз больше массы электрона. Можно сравнить влияние массы переносчика взаимодействия на характер взаимодействия с влиянием избыточного веса на достижения атлета. Чем он тяжелее, тем меньше расстояние, на которое он может прыгнуть, чтобы достать другую частицу.

Теория струн является также и теорией сил. Вернёмся к аналогии с танцорами. Представьте себе, как две цепочки взявшихся за руки танцоров приближаются друг у другу. Всё это время, за исключением короткого промежутка времени, когда они соединяются в одну цепочку, они исполняют разные танцы. Перед тем как встретиться, от одной из цепочек отделяется группа танцоров, которые образуют третью короткую цепочку. Эта третья цепочка направляется ко второй группе и соединяется с ней.

Так две первоначальные группы постоянно обмениваются короткими цепочками, и это порождает действующую между ними силу.

Издалека мировой лист, описывающий этот обмен, выглядит как буква «Н», но «под микроскопом» линии, образующие эту букву, превращаются в подобие водопроводных труб. Поперечная палочка буквы «Н» – это мировой лист обменной струны, которая летает туда-сюда между вертикальными палочками и создаёт действующую между ними силу. В первые дни теории струн те из нас, кто надеялся объяснить с её помощью всё, что имеет отношение к адронам, испытывали восторг от открывающихся перспектив описания ядерных сил, удерживающих протоны и нейтроны в ядре.

К несчастью, наши надежды очень скоро рухнули. Когда были выполнены первые расчёты, стало понятно, что полученный закон, описывающий силы между струнами, не имеет ничего общего с законом, которому подчиняются силы, удерживающие нуклоны вместе. Вместо короткодействующих ядерных сил мы получили дальнодействующие силы, скорее напоминающие электромагнитные или гравитационные, о чём я уже упоминал ранее. Обнаружить причину этого оказалось несложно. Среди похожих на частицы вибрирующих струн были два объекта с очень специфическими свойствами. Первый – открытые струны типа тех, которые описывают мезоны, а второй – замкнутые струны, описывающие глюболы. Оба этих объекта отличались тем, что не имели массы, – точно так же, как фотоны и гравитоны! При обмене этими объектами между частицами возникали силы – почти такие же, как электрические силы между зарядами или гравитационные силы между массами. Открытые струны вели себя как фотоны, но наибольшим сюрпризом для меня оказалось то, что замкнутые глюболы вели себя точно так же, как в теории должны вести себя неуловимые таинственные гравитоны. Это всё могло бы стать источником бесконечной радости, если бы мы собирались построить новую теорию гравитации и электромагнетизма, но это было весьма далеко от нашей цели. Ведь мы-то хотели описать ядерные силы, и в этом смысле все наши попытки потерпели сокрушительный провал. Мы оказались в тупике.

В теории струн есть ещё одна трудность. Она одновременно является «теорией всего» и «теорией ничего». Первоначальной целью теории было описание адронов, и ничего больше. Электроны, фотоны и гравитоны оставались точечными частицами. Многолетние эксперименты убеждали нас, что если электроны и фотоны и имели какие-то размеры, то были гораздо меньше адронов. Они с таким же успехом могли быть просто точками, если так можно выразиться. С другой стороны, было очевидно, что адроны точками быть никак не могут. Точка не может вращаться вокруг собственной оси. Думая о вращающемся объекте, я представляю себе кусок теста, который вертит повар, готовящий пиццу, или баскетбольный мяч, который баскетболист крутит на пальце. Но невозможно представить себе вращение бесконечно малой точки. Адрону очень легко придать вращение: возбуждённые вращательные состояния адронов регулярно наблюдаются в экспериментах на ускорителях. Адроны должны быть больше похожи на кусок теста, чем на математическую точку. Но никому ещё не удалось заставить вращаться электрон или фотон.

Реальные адроны могут взаимодействовать и взаимодействуют с точечными частицами. Протон способен поглощать и испускать фотоны точно так же, как это делает электрон. Но как только мы пытаемся построить теорию, в которой струнноподобный адрон взаимодействует с фотоном, всё летит к чёрту. Одно математическое противоречие за другим разрушает все наши попытки.

И тут сразу многим пришла в голову очевидная идея. Колеблющаяся струна – разумеется, не точка, но мы всегда считали, что на концах струны находятся точечные кварки. Почему бы не считать, что и весь электрический заряд струны тоже сосредоточен на этих кварках? После этого останется лишь просчитать взаимодействие фотонов с точечными зарядами – детская задача. Но, как известно, порой даже лучшие планы идут наперекосяк.

Проблема в том, что струны в теории струн обладают исключительно сильной квантовой дрожью. Чрезвычайно высокочастотные квантовые флуктуации оказываются настолько дикими и неконтролируемыми, что кварки, находящиеся на концах струны, могут оказаться на самом краю Вселенной. Это звучит глупо, но части струны вибрируют настолько сильно, что в очень короткие промежутки времени могут оказываться бесконечно далеко!

Я попытаюсь объяснить такое интуитивно непонятное поведение струн на простом примере. Представьте себе гитарную струну. Она несколько отличается от струн струнной теории, в первую очередь тем, что концы гитарных струн неподвижно закреплены на концах грифа и деки. Но сейчас это не важно. Важным является то, что струны обоих видов могут иметь различные моды колебаний. Гитарная струна может колебаться как единое целое, двигаясь, как детская скакалка. Когда возбуждена эта мода колебаний, струна звучит как основной тон.

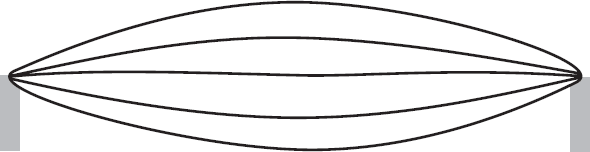
Но, как известно любому гитаристу, струны могут звучать и на обертонах высших гармоник. При этом струна колеблется не как единое целое, а как одна или несколько струн, соединённых последовательно своими концами. Например, в моде первой гармоники струна колеблется, как будто она разделена пополам: середина струны остаётся неподвижной.

В принципе, идеальная бесконечно тонкая струна может иметь бесконечное количество мод колебаний и излучать обертона бесконечно высоких гармоник, но на практике трение и другие факторы демпфируют колебания высших гармоник, не давая им даже возбудиться.

Теперь вспомним урок квантовой механики из главы 1. Любой осциллятор обладает неустранимыми нулевыми колебаниями. Это имеет весьма драматические последствия для идеальной струны: все возможные колебания, весь бесконечный набор колебательных мод звучит одновременно, создавая безумную симфонию белого шума. Если мы просуммируем вклад всех мод колебаний для какого-нибудь отдельно взятого фрагмента струны, то обнаружим, что максимальная амплитуда его колебаний является бесконечной.

Почему же эта безумная какофония не возникает при звучании обычной гитарной струны? Причина заключается в том, что обычные струны состоит из атомов, располагающихся вдоль струны. Не имеют смысла моды колебаний, при которых расстояние между узлами стоячей волны на струне меньше, чем расстояние между соседними атомами. Но математически идеальная струна не состоит из атомов, и количество узлов на струне фиксированной длины может быть любым, поэтому она будет колебаться совершенно неконтролируемым образом.

Пожалуй, самое удивительное математическое чудо теории струн заключается в том, что если посчитать всё корректно, то окажется, что в десятимерном пространстве-времени струны колеблются синхронно и ни одна не улетает на бесконечность относительно другой. Иными словами, ваша струна и моя струна могут колебаться с размахом от одного края Вселенной до другого, но если мир десятимерен, мы чудесным образом не обнаружим эти колебания.

Но это чудо работает, только если всё в мире состоит из струн. Если фотон является точечной частицей, а протон – струной, возникнет ужасная коллизия. По этой причине только струна может взаимодействовать с другими струнами! Это именно то, что я имел в виду, когда я говорил, что теория струн является теорией всего или теорией ничего.

Яростная струнная квантовая дрожь, размах колебаний которой достигает границ Вселенной, казалась столь мрачной перспективой, что я отбросил все мысли о негибкой математике теории струн более чем на десять лет. Но в конце концов это берсеркоподобное поведение струн стало основой для одной из самых интересных и странных разработок современной теоретической физики. В главе 10 мы познакомимся с голографическим принципом, который гласит, что мир является своего рода квантовой голограммой на границах пространства. В какой-то степени открытие этого принципа было вдохновлено экстремальной квантовой дрожью струн. Но голографический принцип – это особенность квантово-механического описания гравитации, а не ядерной физики.

Некоторые теории настолько математически точны, что теряют гибкость. Это хорошо, если теория успешна. Но если что-то в теории работает не совсем так, как хотелось бы, то негибкость становится помехой. Варианты теории струн, существовавшие в 70-х, 80-х и большей части 90-х, не позволяли описать взаимодействие объектов, которые не являются струнами. Если ваша цель – описать взаимодействие адронов, то такая теория для вас не слишком многообещающая. Слишком много измерений, безмассовые гравитоны и фотоны и невозможность взаимодействия с более мелкими объектами… В общем, теория струн испытывала серьёзные трудности, по крайней мере в качестве теории адронов. Тем не менее никто не отрицал, что адроны ведут себя как упругие струны с кварками на концах. За 35 лет, прошедших со времени создания теории струн, струнная природа адронов стала хорошо проверенным экспериментальным фактом. Но в то же время теория струн нашла себя в другой жизни. Следующая глава посвящена тому, как теория струн возродилась в виде фундаментальной теории, объединяющей квантовую механику и общую теорию относительности.