Понимание условий применения и пределов моделей решений возвращают нас к вопросу о базовых ставках, обсуждавшемуся в главе 6. В примерах с такси и медицинскими исследованиями мы видели: люди не думают в терминах условных вероятностей. Они не часто обращают внимание на общую численность населения, высказывая суждения о конкретных событиях.

В тех примерах нам были представлены все недостающие факты, так что для расчета условных вероятностей требовалось просто взять формулу и подставить цифры. Но, как мы знаем, очень часто у нас нет данных: их требуется найти, и они не фиксированные, а изменчивые. В таких случаях мы можем включать в наши модели новую информацию в рамках байесовского процесса обновления.

Но давайте будем осторожны. То, что помогает точно предсказывать температуру или прогнозировать результаты баскетбольной команды, может оказаться не особенно полезным в других случаях. Иные временные рамки и события, в которых мы заинтересованы, могут повлиять на обновление модели.

Рассмотрим прогноз погоды. Проводя измерения каждый день, мы можем обновлять наши модели так, чтобы с течением времени они становились все точнее и точнее. Постоянное улучшение прогнозирования температуры – в начале 1970-х средняя ошибка составляла 6 градусов, в 1990-е годы 5 и всего 4 градуса в 2010-м – явно свидетельствует о пользе обновления моделей. Здесь мы не только располагаем большим объемом данных, но и имеем дело с тем, на что не можем непосредственно влиять (по крайней мере, во временных рамках прогноза – как мы узнали, со временем климат можно изменить). То же касается моделей, которые прогнозируют производительность баскетбольной команды. Наша цель – составить прогноз на то, на что мы не влияем ни прямо (не гоним мяч в лунку и не бьем), ни косвенно (Никс и Лейкерс не знают, что прогнозирует наша модель). Поскольку каждую неделю проводится несколько игр, мы можем постоянно совершенствовать свои модели. Правильно считать, что они находятся в состоянии разработки и регулярно дополняются, чтобы с течением времени становиться точнее.

В книге «Сигнал и шум» Нейт Сильвер использует интересный пример, дающий представление о том, насколько полезными могут быть условные вероятности и байесовские обновления. Предположим, вы женщина, живете с приятелем и по возвращении из командировки обнаруживаете в ящике комода чужое нижнее белье – явно женское. Поэтому вы начинаете думать, что у вашего друга есть связь на стороне.

Сильвер объясняет: если мы рассчитаем три базовые ставки – исходную вероятность без учета доказательств, истинную положительную частоту и ложную положительную частоту, – то теорема Байеса может обеспечить хорошую начальную оценку. Во-первых, нужно сделать оценку вероятности без учета текущего доказательства, что партнер завел интрижку. При отсутствии другой информации мы можем использовать общую базовую ставку неверности, которую Сильвер принимает за 0,04. Во-вторых, мы должны оценить вероятность, что белье могло появиться вследствие его измены, что Сильвер принимает за 50 %, или 5,33.

В-третьих, вероятность, что белье появилось, но он не изменял, Сильвер оценивает в 5 % или 0,05. Мы не знаем наверняка, правильны ли эти показатели, но они хорошая отправная точка для оценки того, что нас интересует, – вероятности измены, с учетом того, что обнаружено нижнее белье. Идея байесовского обновления в том, что если мы сделаем первичный расчет, а затем длительное время, скажем, полгода, будем собирать дополнительные данные, то, периодически пересматривая свою модель, мы получим все более точные оценки.

До сих пор все шло хорошо. Применив теорему Байеса, как в примере с такси и медицинским исследованием, мы получим цифры, представленные в табл. 9.1. Существуют две вероятности появления белья: одна – что партнер не завел интрижку (5 % от 96, или 4,8 %) и вторая – что он ее завел (50 % от четырех, 2 %). Вероятность интрижки с учетом таинственного белья рассчитывается следующим образом: 0,02 / (0,02+ + 0,048) = 294, или 29,4 %.

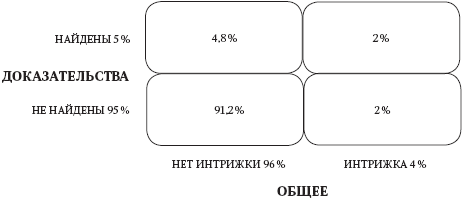
Рис. 9.1. Была ли интрижка

Учитывая явную улику, это явно меньше, чем вы себе представляли, но так говорят цифры. А как насчет остальных 70,6 %? Расслабьтесь. Тут нет никакого жульничества: просто ошибка прачечной, или белье осталось после приезда родственницы, или другое невинное объяснение.

Забавный пример, приводящий преподобного Байеса, так сказать, в спальню. Но не лучший способ показать, как с помощью постоянного обновления модели становятся все более и более точными. В нем не учитывается ни важность быстрого обновления, ни то, как факт измерений может повлиять на вероятность будущих событий.

Чтобы понять, что я имею в виду, допустим, что на основе этих предположений вы выяснили: шансы на то, что ваш партнер имеет отношения на стороне, составляют 29,4 %. Если бы речь шла о завтрашней погоде, мы знали бы, что делать дальше. Мы бы записали завтрашнюю температуру, сравнили ее со своим прогнозом, а затем подкорректировали бы модель, чтобы сделать лучший прогноз в следующий раз. То же самое мы сделаем, если захотим предсказать, сколько очков, скорее всего, выиграет Knicks: сделаем прогноз, узнаем результат матча и уточним свою модель, чтобы сделать лучший прогноз для следующей игры. Процесс работает, когда мы быстро получим новые точные данные, а самое главное, когда сбор информации не изменяет вероятности будущего. В конце концов, погода не знает, что вы спрогнозировали, и команда Knicks не знает, как ее оценила ваша модель. Вы не влияете на результаты ни прямо, ни косвенно.

Но когда речь заходит об обнаружении загадочного нижнего белья, все меняется. Как именно вы определите, действительно ли ваш партнер завел роман, а затем настроите модель, чтобы сделать прогноз более точным, не изменяя вероятности будущего события? Если вы зададите вопрос – даже не прямой, типа «Ты завел интрижку?», а более мягкий, например «Хотелось бы знать, Джи, чье это нижнее белье?», – то измените вероятность будущего события. Если до этого ничего не происходило, то ваш вопрос вряд ли сделает ее более вероятной, но если у вашего партнера действительно роман, то он постарается лучше скрывать его в будущем, что снизит вероятность появления нижнего белья в комоде. Или ваш партнер может тихо прекратить отношения, что опять приведет к снижению вероятность повтора. В любом случае, само усилие узнать правду создает виток обратной связи, что отличает этот пример от предсказания погоды или счета в баскетбольном матче.

Может быть, вы решите ничего не говорить и не делать. Вы ведете себя так, как будто ничего не случилось, и наблюдаете, что произойдет дальше. Это вызывает другую проблему: ожидание повторного появления белья может занять много времени, особенно если вы ездите в командировки один раз в месяц. Вы не сможете собрать данные достаточно быстро, чтобы обновить модель в значительной степени, и, конечно, недостаточно быстро, чтобы пролить свет на этот животрепещущий вопрос. Байесовское обновление может быть очень мощным, но мы должны признать его практические пределы.