Чтобы проиллюстрировать, как повышение производительности (абсолютное) может повлиять на успех (относительный), давайте вернемся к примеру из главы 2: в нем игроков просили забить мяч в лунку (опустим проектор и круги, создававшие иллюзию увеличения и уменьшения лунки).

Давайте предположим, что группа начинающих игроков в гольф при ударе с двухметрового расстояния имеет 30-процентный шанс попадания. Если мы попросим каждого из них сделать по 10 ударов (и предположим, что каждый удар независимый, то есть один удар не улучшает качество других), то получим распределение, представленное на рис. 4.1. Очень небольшое количество игроков (2,8 %) промахнется все десять раз, 12 % попадет в одну лунку, 23,3 % в две и 26 % (самый распространенный результат) в три. От этой точки кривая распределения начинает снижаться: в четыре лунки попадет 20 % игроков, 10,3 % попадет в пять и 3,7 % в шесть лунок. В семь лунок из десяти попадет менее 1 %, и хотя дальнейшее улучшение возможно, оно все менее и менее вероятно.

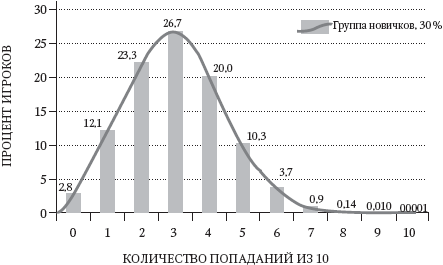
Рис. 4.1. Группа новичков, 30-процентный уровень попаданий

Теперь предположим, что мы собрали другую группу и провели для нее занятия. Мы обучили участников делать плавный удар с хорошим завершением. Мы научили их сосредоточивать ум и использовать преимущества позитивного мышления. Давайте предположим, что члены обученной группы попадают в 40 % случаев – значительное улучшение по сравнению с 30 % у новичков, но все еще далекое от 54,8 % – у профессиональных гольфистов, упомянутых в главе 2. Если все члены группы сделают по 10 ударов, то получится распределение как на рис. 4.2. Теперь почти никто не промажет все десять раз: 4 % попадут только в одну лунку, 12,1 % в две, 21,5 % в три, 25,1 % в четыре и т. д.

Если мы наложим результат новичков на результат обученных гольфистов, как это показано на рис. 4.3, то увидим, что они не сильно различаются.

В любых соревнованиях некоторые новички сыграют лучше, чем обученные профессионалы.

А теперь вопрос: если мы проведем соревнование между новичками и обученными гольфистами (скажем, по 30 человек в обеих группах) и каждый сделает по 20 ударов, то каковы шансы у одного из членов первой и у одного из членов второй группы занять первое место? Конечно, более вероятно, что победит обученный гольфист, но насколько? Есть ли шанс, что победителем станет новичок, или это маловероятно?

Чтобы выяснить это, я использовал моделирование Монте-Карло, метод, разработанный в 1940 году, когда ученым из Манхэттенского проекта понадобилось предсказать исход цепных ядерных реакций. Физика цепных реакций настолько сложна, что точный расчет в этом случае был невозможен. Легче было рассчитать, что произойдет в целом ряде испытаний, а затем, объединив результаты, получить представление о распределении возможных исходов. Ученые Джон фон Нейман и Станислас Улам назвали свой метод в честь Монте-Карло – казино в Монако с его знаменитой рулеткой. При любом однократном вращении колеса рулетки шар попадает только на один слот, из чего мы получим мало информации. Но поверните колесо рулетки тысячу раз, и получите представление о том, что может случиться.

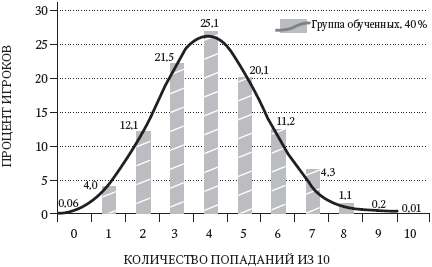
Рис. 4.2. Группа обученных: 40-процентный уровень попаданий

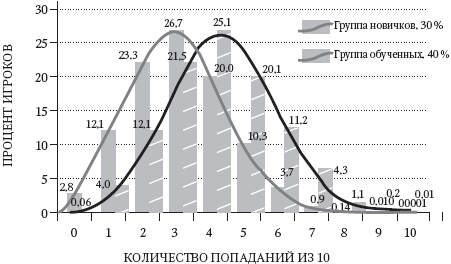
Рис. 4.3. Объединение групп начинающих (30 %) и обученных (40 %)

Изучая влияние изменения абсолютной производительности на относительную, я провел имитационные эксперименты по методу Монте-Карло, чтобы иметь результаты тысячи соревнований, где 30 новичков и 30 обученных гольфистов делают по 20 ударов. Результаты показали: 86,5 % времени, в 865 из 1000 испытаний победителями стали члены обученной группы. 9,1 % времени сохранялось преимущество группы обученных, и только 4,4 % времени, всего 44 раза из 1000 испытаний, самый высокий результат был получен в группе начинающих. Абсолютное преимущество группы обученных, 40-процентное попадание по сравнению с 30-процентным, обеспечивало своим членам почти непреодолимое относительное преимущество. Лучшие начинающие побеждали всех 30 обученных игроков реже одного раза из 20.

А что, если бы выигрыш от обучения был бы намного меньше – например, меткость повысилась бы от 30 до всего лишь 33 %? Если обученная группа будет иметь распределение, как на рис. 4.4, то перекрытие с группой начинающих станет значительно больше, как показано на рис. 4.5. Вероятность того, что новичок сможет выиграть, должна повыситься, и мы действительно это наблюдаем. Тем не менее метод Монте-Карло показал: в соревновании, где 30 членов каждой группы сделают по 20 ударов, член группы начинающих закончит победителем в 19,9 % случаев (в 199 из 1000 испытаний). Член группы обученных победит в 55,5 % случаев (555 из 1000), и в 24,6 % счет будет равным. Даже относительно небольшое улучшение, с 30 до 33 %, обеспечивает группе обученных более чем двукратное преимущество.

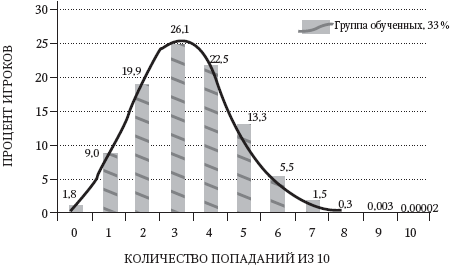
Рис. 4.4. Группа обученных: 33 % попаданий

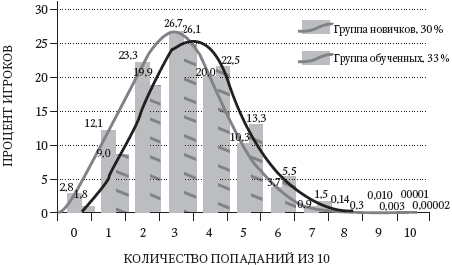
Рис. 4.5. Объединение группы начинающих (30 %) и группы обученных (33 %)

Урок ясен: в условиях конкурентной борьбы даже умеренное повышение абсолютной производительности может оказать огромное влияние на относительную производительность. И наоборот, неспособность использовать все возможные преимущества для повышения абсолютной производительности оказывает сокрушительное действие на вероятность выигрыша. В этих условиях насущная необходимость – поиск способа повысить эффективность.