Книга: Таинственные страницы. Занимательная криптография
Назад: Этюд XXV Игры Клода Шеннона
Дальше: Этюд XXVII О пользе знания языков
Этюд XXVI
Дешифровка линейного письма Б
В сборнике задач для олимпиад по криптографии и математике для школьников приведен следующий фигурный цифровой кроссворд:
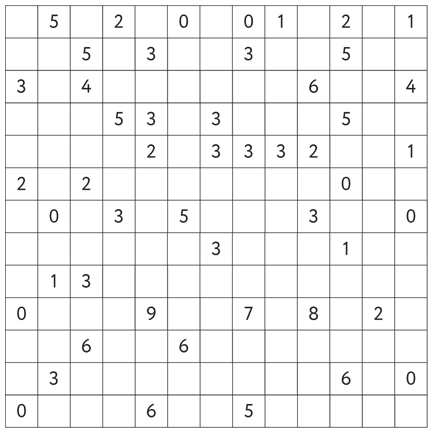
Условия задачи таковы: числа, расположенные в клетках таблицы, указывают, сколько соседних по горизонтали, вертикали и диагонали клеток (может быть включена и та клетка, в которой находится само число) должны быть окрашены. Восстановите картинку, которой соответствуют эти числа.
Наверное, это одна из самых легких задач в этом сборнике. Но при чем тут криптография? На рисунке, конечно, изображено что-то, что может ассоциироваться с секретами, тайнами.
Дадим вам ключ к решению этого кроссворда – на картинке в том числе изображен самый обычный ключ для запирания двери.
Эта задача тренирует пространственное мышление. Постепенно «откапывая» куски, «орнаменты» кроссворда, вы будете формировать из зрительных образов закономерности, предугадывая рисунок. Однажды такой способ мышления пригодился для разгадывания критского линейного письма Б.
Линейное письмо Б – позднейшая форма критского письма (XV–XII века до н. э.), которая использовалась для записи текстов на древнегреческом языке в эпоху микенской культуры.
Микенские тексты – слоговая фонетическая письменность, каждый знак которой является слогом типа «согласный звук плюс гласный звук». Единственный нефонетический знак – словоразделитель (пробел), он играет очень важную роль в ходе любой дешифровки.
В 1900 году первооткрыватель линейного письма Б археолог сэр Артур Эванс (1851–1941) заметил на одной из глиняных табличек слово, состоящее из двух слоговых знаков и третьего знака-детерминатива «лошадь без гривы»: 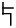

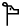 . Это слово было похоже по написанию на
. Это слово было похоже по написанию на 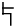

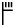 из кипрского силлабария, которое было уже дешифровано как po-lo (третий слог se здесь немой). Эванс сопоставил po-lo с греческим põlos (жеребенок, родственно англ. foal). Такое прочтение оказалось правильным. Но после этого прогресс в деле дешифровки застопорился.
из кипрского силлабария, которое было уже дешифровано как po-lo (третий слог se здесь немой). Эванс сопоставил po-lo с греческим põlos (жеребенок, родственно англ. foal). Такое прочтение оказалось правильным. Но после этого прогресс в деле дешифровки застопорился.
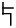

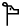 . Это слово было похоже по написанию на
. Это слово было похоже по написанию на 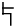

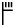 из кипрского силлабария, которое было уже дешифровано как po-lo (третий слог se здесь немой). Эванс сопоставил po-lo с греческим põlos (жеребенок, родственно англ. foal). Такое прочтение оказалось правильным. Но после этого прогресс в деле дешифровки застопорился.
из кипрского силлабария, которое было уже дешифровано как po-lo (третий слог se здесь немой). Эванс сопоставил po-lo с греческим põlos (жеребенок, родственно англ. foal). Такое прочтение оказалось правильным. Но после этого прогресс в деле дешифровки застопорился.Дело сдвинулось с мертвой точки только через тридцать лет благодаря работам профессора классической филологии Алисы Кобер (1906–1950) из Бруклинского колледжа, США. Еще будучи студенткой, А. Кобер занималась исследованиями в различных направлениях, от астрономии и математики до естественных наук, никогда не ограничивая себя изучением только классических языков. Видя, что филологи застопорились в деле дешифровки линейного письма Б, она применила статистический подход, анализируя символы табличек. Алиса не пыталась установить фонетические значения знаков, не пробовала угадать смысл отдельных слов, не делала даже предположений о языке письма. Зато она обратила внимание, что часть слов образует «тройки», то есть одно и то же слово встречалось в тексте в трех слегка различающихся формах. Корень слова всегда был неизменным, но существовало три разных окончания.
Табл. 7. Два склоняемых слова в линейном письме Б
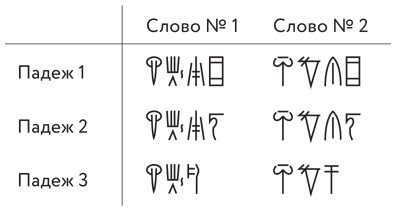
Как видим, первые два знака в обоих словах в табл. 7 образуют корень. Трудности начинаются с третьим символом. Если он часть корня, то должен быть одинаковым во всех падежах (но в третьем падеже его нет!). В противном случае, если третий символ не является частью корня, он должен быть частью окончания. Но ведь для разных слов окончания должны быть одинаковыми во всех падежах. А мы видим, что рассмотренные в табл. 7 слова совпадают в окончаниях только для первых двух падежей, но для третьего падежа это не так. Парадокс: третьи символы не являются ни частью корня, ни частью окончания.
Кобер разрешила эту проблему. Она предположила, что третий слог соединительный, то есть является и частью корня, и частью окончания слова. В качестве примера (табл. 8) она рассмотрела слово из аккадского языка – sadanu, имеющее корень sad и окончание anu в первом падеже.
Табл. 8. Соединительные слоги в аккадском слове sadanu
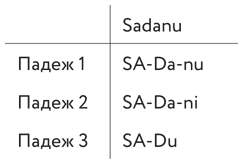
Здесь второй, соединительный слог меняется от -da к -du (корень для наглядности выделен заглавными буквами).
Продолжил дело Алисы Кобер английский архитектор Майкл Вентрис (1922–1956). Еще четырнадцатилетним школьником Вентрис побывал на популярной лекции Артура Эванса, посвященной в том числе и линейному письму Б. Майкл всерьез увлекся этой темой и решил дешифровать линейное письмо, но все же «ему самому казалось, что изучение старинных загадочных письмен не дело, а интересное и увлекательное времяпрепровождение, вроде решения кроссвордов [выделено мной. – И. Е.]. Поэтому, окончив школу, он ‹…› поступил в архитектурный институт в Лондоне, так как и архитектура его с детства очень интересовала».
Майкл Вентрис окончательно, в июне 1951 года, дешифровал каждый символ, установил, что язык письма – греческий, и сопоставил каждому символу (слогу) его фонетическое звучание. Так, слово 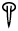


 – столица минойского Крита, город Кносс, по слогам линейного письма Б читается как ko-no-si-ja.
– столица минойского Крита, город Кносс, по слогам линейного письма Б читается как ko-no-si-ja.
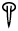


 – столица минойского Крита, город Кносс, по слогам линейного письма Б читается как ko-no-si-ja.
– столица минойского Крита, город Кносс, по слогам линейного письма Б читается как ko-no-si-ja.Так что же предопределило успех английского гения Вентриса в деле дешифровки? Несомненно, ему помогло то, что он свободно говорил на шести европейских языках (и кроме того, немного знал русский), владел древнегреческим и латынью. Он применил математические методы для анализа текста глиняных табличек. Но было еще кое-что, что помогло ему.
Соратник Вентриса, преподаватель классических языков в Кембридже Джон Чедвик писал о нем: «Его мозг работал с поразительной быстротой… Микенцы были для него не смутной абстракцией, а живыми людьми… [Он] настолько хорошо знал [неразгаданные] тексты, что большие куски запечатлелись в его мозгу просто как зрительные образы… и вот тут-то пригодилось его архитектурное образование [выделено мной. – И. Е.]. Глаз архитектора видит в здании не единственно лишь внешнюю сторону – беспорядочную мешанину декоративных элементов ‹…› он способен разглядеть то, что находится за ней: важные части орнамента, элементы конструкции и корпус здания. Так и Вентрис сумел разглядеть среди приводящего в замешательство многообразия загадочных символов и рисунков закономерности, которые раскрыли лежащую за ними внутреннюю структуру. Именно этим качеством – способностью разглядеть порядок в кажущемся беспорядке – характеризуются деяния всех великих людей».
Таким образом, как зрительное восприятие, так, возможно, и увлечение кроссвордами немало поспособствовали Майклу Вентрису в окончательной дешифровке линейного письма Б.
Осталось только привести решение фигурного кроссворда:

Назад: Этюд XXV Игры Клода Шеннона
Дальше: Этюд XXVII О пользе знания языков

