Небесные координаты

Назад: Восход и заход светил. О кульминации

Дальше: Астрономическая и астрологическая структуры Солнечной системы

Системы координат

Положение любой точки на плоскости может быть определено при помощи различных систем координат. Числа, определяющие положение точки, называются ее координатами. Наиболее употребительные системы координат для плоскости – декартова прямоугольная система и полярная система.

Прямоугольными координатами точки P (рис. 7а) называются взятые с определенным знаком расстояния (выраженные в определенном масштабе) от двух перпендикулярных линий, называемых осями координат. Точка пересечения осей называется началом координат. Обычно горизонтальную ось (ось ОХ) называют осью абсцисс, а вертикальную (ось ОУ) – осью ординат. На этих осях устанавливается положительное направление, обычно на оси ОХ – вправо, на оси ОУ – вверх.

Полярными координатами точки Р (рис. 7б) называются радиус-вектор ρ – расстояние от точки Р до заданной точки О (полюса) и полярный угол φ – угол между прямой ОР и заданной прямой, проходящей через полюс (полярной осью). Полярный угол считается положительным при отсчете от полярной оси против часовой стрелки и отрицательным при отсчете в обратную сторону.

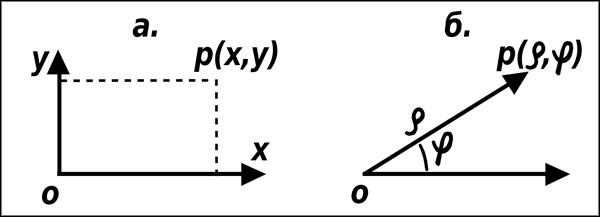
Рис. 7. Системы координат на плоскости: а) прямоугольная система; б) полярная система

Теперь переходим от плоскости к трехмерному пространству, где пользуются прямоугольными, цилиндрическими и сферическими координатами. Прямоугольными координатами точки называются расстояния, взятые от этой точки до трех взаимно перпендикулярных плоскостей, или, что то же самое, проекции радиуса-вектора точки Р на три взаимно перпендикулярные оси (рис. 8а). Здесь к абциссе и ординате добавляется еще третья координата – аппликата OZ.

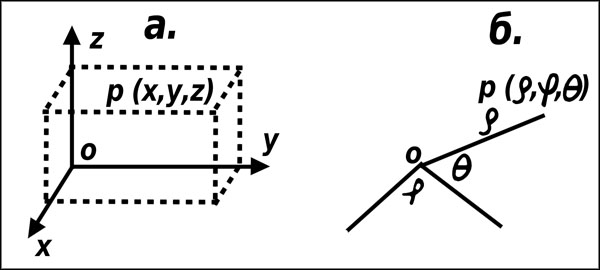
Рис. 8. Системы трехмерных координат: а) прямоугольная система; б) сферическая система

Цилиндрические координаты нас не интересуют, а вот сферические – это аналог полярных координат на плоскости (рис. 8б). Это ρ – радиус-вектор точки Р в пространстве, q – полярное расстояние между радиус-вектором и заданной плоскостью и угол φ – расстояние между проекцией радиуса-вектора на заданную плоскость и заданной прямой на этой заданной плоскости.

Положение точек на небесной сфере, в частности светил, определяется сферическими координатами. Наиболее употребительными являются три системы сферических небесных координат: горизонтальная, экваториальная и эклиптическая.

В любой из них положение точки определяется двумя координатами, одна из которых дает угловое расстояние этой точки от плоскости некоторого основного круга, например горизонта, экватора или эклиптики (аналогично географической широте), а другая отсчитывается от проекции на плоскость этого круга радиуса-вектора определяемой точки, до определенной фиксированной точки на указанном круге, принятой за начало (аналогично географической долготе). Третья координата – радиус-вектор – здесь не рассматривается по вышеуказанным причинам.

Мы рассмотрим все три системы координат, однако пользоваться в основном будем эклиптической системой.

Горизонтальная система координат

Горизонтальная система координат характеризуется высотой и азимутом (рис. 9).

1. Высота (h) отсчитывается от горизонта до данной точки M по большому полукругу, проведенному через точку от зенита. Она изменяется от –90° под горизонтом до 90° над горизонтом.

2. Азимут (А) отсчитывается от точки юга – S по часовой стрелке вдоль горизонта до его пересечения с кругом высоты данной точки. Изменяется азимут от 0° до 360°.

В этой системе высота и азимут являются переменными величинами и зависят от географических координат точки и времени. Это динамичная система координат.

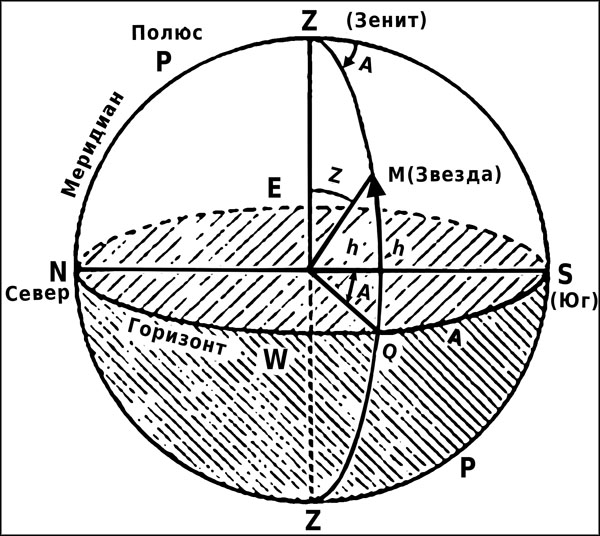
Рис. 9. Горизонтальная система координат

Там, где экватор совпадает с горизонтом, везде юг или север. Это имеет место, когда мы пытаемся определить координаты Северного или Южного полюса.

Экваториальная система координат

Экваториальная система координат характеризуется склонением и прямым восхождением.

1. Склонение (σ) – это расстояние, отсчитываемое от экватора до данной точки М по большому полукругу, проведенному через эту точку из полюса мира.

Экватор делит небесную сферу на два полушария: Северное и Южное.

Склонение бывает больше нуля в Северном полушарии и меньше нуля в Южном и изменяется от –90° до 90°.

2. Прямое восхождение (α) – это расстояние, отсчитываемое от точки весеннего равноденствия против часовой стрелки, если смотреть со стороны северного полюса мира вдоль экватора до круга склонения.

Обычно оно выражается как в градусах, так и в часах из расчета, что 360° = 24 часа и изменяется от 0° до 360° или от 0 до 24 часов.

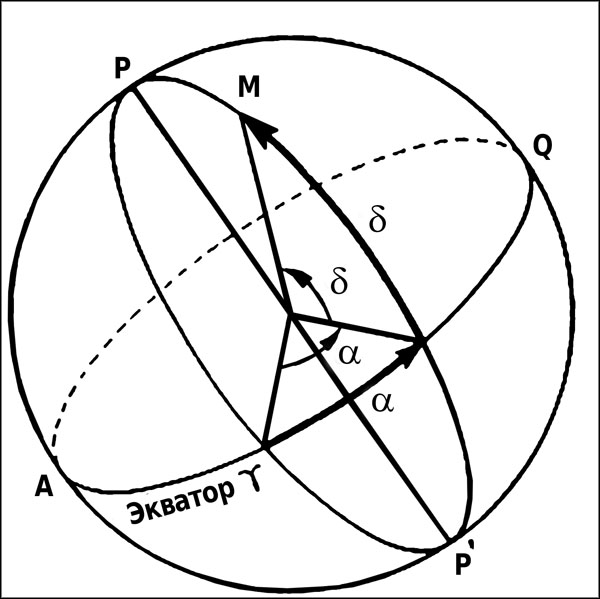
Рис. 10. Экваториальная система координат

Эклиптическая система координат

Эклиптическая система координат характеризуется эклиптическими или астрономическими широтой и долготой. Мы будем называть их просто широтой и долготой, имея в виду, конечно, их отличие от географических широты и долготы (рис. 11).

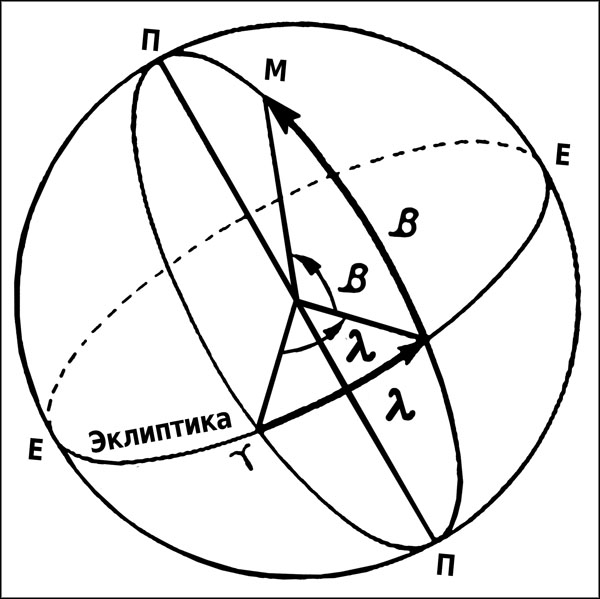
Рис. 11. Эклиптическая система координат

1). Широта (b) – это расстояние, отсчитываемое от эклиптики до данной точки М по большому полукругу, проведенному через эту точку из полюса эклиптики.

2). Долгота (l) – это расстояние, отсчитываемое от точки весеннего равноденствия против часовой стрелки, если смотреть из Северного полушария вдоль эклиптики до пересечения с кругом широты.

Эклиптика так же, как и экватор, делит небесную сферу на два полушария: Северное и Южное, только в обоих случаях полушария будут несколько не совпадать.

Как можно заметить, эклиптическая система очень похожа на экваториальную. Те же самые правила, только слово «экватор» заменяется на слово «эклиптика», круг склонения – на круг широты и полюс мира – на полюс эклиптики, склонение – на широту, а прямое восхождение – на долготу.

Широта, как и склонение, изменяется в пределах от –90° до 90°, а долгота, как и прямое восхождение, от 0 до 360° или от 0 до 24 часов. Они так же, как склонение и прямое восхождение, не зависят ни от времени, ни от места наблюдения.

В астрономии чаще пользуются экваториальной системой координат, в астрологии же – преимущественно эклиптической, остальные системы играют вспомогательную роль. Во многих справочниках и астрономических календарях приводятся экваториальные координаты, потому что они более удобны для наблюдения. Но поскольку плоскости орбит большинства планет очень близки к плоскости эклиптики, нагляднее приводить координаты планет в эклиптической системе. Поэтому в принципе необходимо уметь делать переход от одной системы координат к другой. Формулы перехода от экваториальной системы в эклиптическую описаны в работе Е.П. Левитана «Астрономия» [48].

Рис. 12. Астрологический алфавит: основные астрологические символы

Назад: Восход и заход светил. О кульминации

Дальше: Астрономическая и астрологическая структуры Солнечной системы