Книга: Мозгоускорители. Как научиться эффективно мыслить, используя приемы из разных наук
Назад: Часть V. Мышление: прямые и извилистые пути
Дальше: 14. Диалектическое мышление
13. Логика
На рисунке внизу вы видите четыре карточки. Они случайным образом выбраны из набора карточек, на которых с одной стороны написана буква, а с другой — цифра. Пожалуйста, укажите, какую или какие из карточек вы должны перевернуть, чтобы выяснить, соответствует ли действительности следующее утверждение: «Если на одной стороне карточки написана гласная буква, то на другой стороне карточки — четное число». Переверните только те карточки, которые совершенно необходимо перевернуть, чтобы убедиться, что правило соблюдается. Проверьте себя: если вы читаете эту книгу на электронном устройстве, выделите свой выбор желтым цветом. Если вы читаете бумажную книгу, поставьте галочку карандашом.
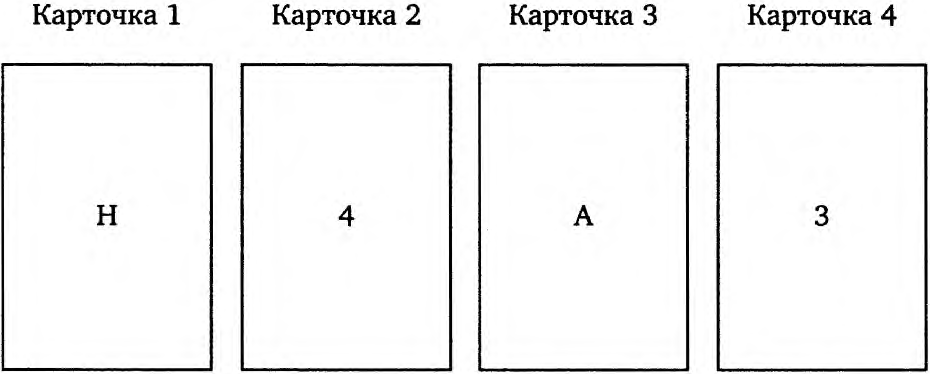
Нужно перевернуть:а) только карточку 3;б) карточки 1, 2, 3 и 4;в) карточки 3 и 4;г) карточки 1, 3 и 4;д) карточки 1 и 3.
К этой задаче мы вернемся чуть позже.
Учебники по критическому мышлению обычно щедро приправлены формальной, дедуктивной логикой. Причем делается это скорее потому, что так было принято в древней педагогической традиции, чем потому, что это приносит пользу в повседневной жизни. Я бы даже сказал, что, возможно, большая часть сведений о формальной логике, которые вы узнаете из этой главы, имеет весьма ограниченную ценность для решения проблем в вашей ежедневной жизни.
Тем не менее существует ряд причин, по которым изучать формальную логику все же стоит.
1. Формальная логика важна для науки и математики.2. Эта глава показывает резкий контраст между западной гиперрациональностью и восточной привычкой к диалектическому мышлению. Одну и ту же проблему можно решать с позиций обеих систем логики, но полученные выводы будут разными. Эти две системы также предоставляют отличную основу для взаимной критики.3. Образованный человек должен немного разбираться в базовых формах логического мышления.4. Формальная логика интересна, по крайней мере она интересна многим. (В любом случае в этой главе ее не так уж много!)
История происхождения западной формальной логики такова: Аристотелю надоело слушать жалкие аргументы в спорах на рынке и в собраниях. Поэтому он решил придумать логические шаблоны рассуждений, которые можно было бы применять в спорах, чтобы проанализировать обоснованность (валидность) аргументов. Аргумент является обоснованным, когда (и только тогда!) проистекающие из него выводы являются обязательным следствием предшествующих ему утверждений. Обоснованность не имеет ничего общего с истиной. Аргумент может быть необоснованным, но вывод может быть верным. Если аргумент построен правильно, он обоснован, тем не менее он может быть неправильным.
Концепция обоснованности аргументов важна по многим причинам. Во-первых, вы не хотите позволить кому-то обмануть вас (или обмануться самому), приписывая какому-то выводу правдоподобность только потому, что он следует из определенных предпосылок — в том случае, если эти предпосылки неверны и вывод необязательно следует из них. Во-вторых, мы не хотим позволить себе не доверять каким-нибудь выводам только потому, что они нам не по душе, хотя предпосылки очевидно верны и форма данного аргумента говорит о том, что вывод тоже верен. В-третьих, имея ясное представление о концепции обоснованности, противопоставленной истинности, мы можем оценить, действительно ли данный вывод следует из данных предпосылок, убрав конкретное значение и взглянув на ситуацию отвлеченно, как на абстрактную формулу. А и Б вместо пестиков и тычинок. Формула как минимум покажет нам, что этот вывод следует из исходных данных, поэтому, даже если он чрезвычайно неправдоподобен, мы по крайней мере увидим, что это не результат логической ошибки.
Силлогизмы
Наиболее важным вкладом Аристотеля в учение о формальной логике является понятие силлогизма. Создание силлогизмов превратилось в целый промысел в Средние века, когда монахи сочиняли их десятками. Со времен Средневековья до конца XIX в. философы и просветители считали, что силлогизмы показывают нам образцы правил мышления. В итоге большая часть высшего образования на Западе опирается на эти правила.
Вопрос обоснованности также важен для силлогизмов, которые относятся к категориальному мышлению. В некоторых типах категориального мышления постоянно используются такие указатели множества, как «все», «некоторые» и «никакие». Простые силлогизмы состоят из двух утверждений и одного вывода. Простейший из этих простых силлогизмов, в котором мы редко допускаем ошибку, формулируется так: «Все А являются Б, все Б являются В, значит, все А являются В». Классический пример:
Все клерки — люди.Все люди двуноги.------------------------Все клерки двуноги.
Это доказательство обоснованно, потому что оно логически следует из предпосылок. Вывод также верен.
Все клерки — люди.У всех людей есть перья.------------------------У всех клерков есть перья.
Это доказательство тоже обоснованно, хотя вывод неверен. Неправдоподобность вывода заставляет нас почувствовать, что доказательство тоже неверно. Но если мы подставим А, Б и В вместо клерков, людей и перьев, мы увидим, что доказательство обоснованно. А это может заставить нас по-новому посмотреть на истинность вывода, что может быть полезно.
Доказательство, которое я приведу ниже, не обоснованно, несмотря на то что его предпосылки и вывод, который из них следует, являются истинными (или как минимум чрезвычайно правдоподобными).
Все люди, получающие социальное пособие, бедны.Некоторые бедные люди непорядочны.Следовательно, некоторые люди, получающие социальное пособие, непорядочны.
В абстрактных величинах:
Все А являются Б.Некоторые Б являются В.Следовательно, некоторые А являются В.
Это упражнение перевода данных в абстрактные величины полезно, потому что иногда нам кажется, что вывод является истинным потому, что кажется правдоподобным, и потому, что имеются истинные предпосылки, которые, казалось бы, логически подтверждают вывод. Обнаружив, что доказательство не обосновано, мы избавимся от чувства, что вывод непременно является истинным, и усомнимся в его достоверности. (Чтобы признать необоснованность приведенного выше доказательства, нужно понять, что случаи А являются подгруппой случаев Б.)
С этого места все начинает стремительно усложняться: все А являются Б, некоторые В являются А, некоторые В являются Б. Верно или нет? Никакие А не являются Б, некоторые В являются Б, никакие А не являются В. Верно или нет?
Можно менять эти буквы местами, пока не потемнеет в глазах. В Средние века монахи коротали время, сочиняя подобные высказывания сотнями. Но я согласен с философом Бертраном Расселом, который заметил, что эти силлогизмы были так же бесплодны, как сами монахи. Вот вам и 26 столетий педагогики, уверяющей, что силлогизмы необходимы для эффективного мышления.
Самое важное, что я вынес для себя из изучения категориального логического мышления, это умение строить диаграммы Венна, названные в честь английского логика XIX в. Джона Венна, который придумал, как изображать принадлежность к категориям. Я не перестаю удивляться, насколько они полезны, даже необходимы для представления взаимосвязей между различными категориями.
На рисунке 5 изображено несколько практически полезных примеров, которые дадут вам общее представление об этих диаграммах.
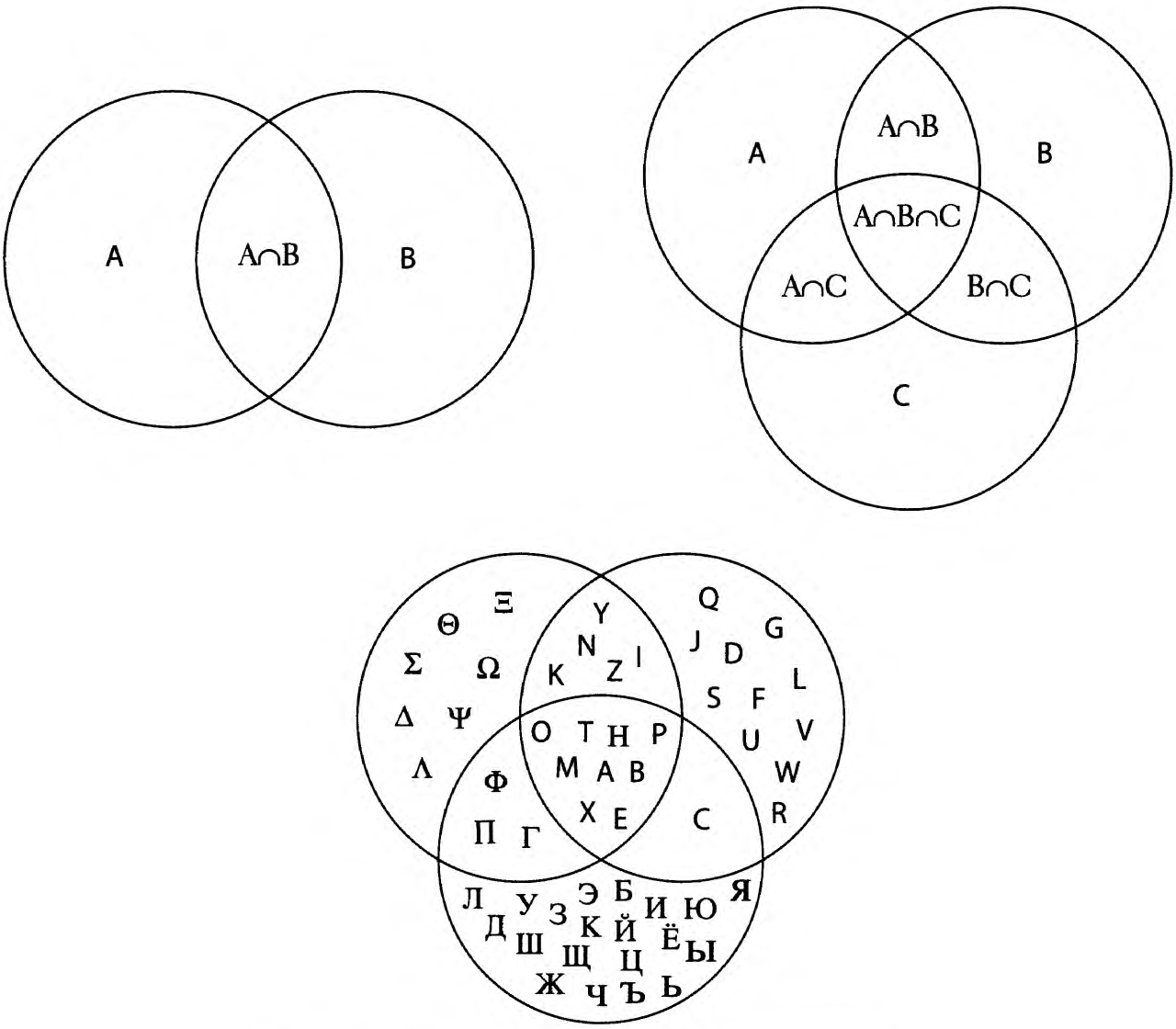
Рис. 5. Область пересечения категорий
Левая верхняя схема на рисунке 5 изображает конкретный силлогизм, который мы используем в повседневной жизни. Этот силлогизм представляет ситуацию, в которой некоторые (но не все) А являются В и некоторые (но не все) В являются А. Например, А означает маленьких пушистых зверьков, а В означает зверьков с утиным клювом. Получается, что на пересечении А и В есть одно животное, а именно — утконос. Также эта схема может демонстрировать ситуацию, когда некоторые, но не все ученики международной школы, говорящие по-английски, также говорят по-французски и некоторые, но не все ученики, говорящие по-французски, говорят по-английски. (Некоторые, но не все А являются В, и некоторые, но не все В являются А.) У тех, кто говорит только по-английски (только А), математику должна преподавать мисс Смит; у тех, кто говорит только по-французски (В), преподавать должен мсье Пиро. Ученики, которые говорят на обоих языках, могут заниматься у любого из этих преподавателей.
Верхняя правая схема показывает гораздо более сложную, но отнюдь не редкую ситуацию, при которой некоторые А являются В, некоторые В являются А, некоторые А являются С, некоторые С являются А, некоторые В являются С и некоторые С являются В.
Нижняя схема демонстрирует реальный пример такой ситуации. На ней изображены области пересечения букв из разных алфавитов: греческого (сверху слева), латинского (сверху справа) и русского (внизу). Ручаюсь, что вам вряд ли удастся прийти к правильному выводу по поводу совпадения данных категорий, используя только вербальные высказывания о них. Уверен, что у меня наверняка получилась бы просто каша из трех алфавитов.
Одних диаграмм Венна, конечно, недостаточно, чтобы подготовить вас к решению всех соответствующих задач, но они могут научить вас основным принципам наглядного изображения принадлежности или непринадлежности к категориям. Возможно, вы поймете, что диаграммы Венна могут оказаться для вас полезны.
Логика высказываний
Силлогизмы можно применять в очень небольшом числе выводов, которые нам приходится делать в повседневной жизни. Гораздо более важно использовать логику высказываний, которая применяется повсеместно.
Философы и логики время от времени обращались к логике высказываний, постепенно развивая эту область науки приблизительно с III в. до н.э. и до XIV в. Начиная с середины XIX в. логики начали делать заметные успехи в области логики высказываний, уделяя особенное внимание таким «операторам», как союзы «и» и «или». «И» служит для «соединения» таких высказываний, как «А верно и В верно; следовательно, А и В верны». «Или» служит для «разъединения», например, «А верно или В верно; А верно, следовательно, В не верно». Именно исследование логики высказываний в то время легло в основу программирования и создания компьютеров.
В начале этой главы я попросил вас решить задачу с карточками. Теперь вы видите, что она требует применения условной логики. Если П, тогда Р. «Если на одной стороне карточки написана гласная, то на другой стороне написано четное число». Перед тем как мы посмотрим, как вы справились с этой задачей, давайте рассмотрим еще одну ситуацию.
Вы инспектор полиции. Одна из ваших обязанностей — проверять, что рестораны не продают алкогольные напитки лицам младше 21 года. Ваша задача — сказать, кого из клиентов вам необходимо проверить, чтобы убедиться, что он не нарушает правила «Если клиент пьет алкогольный напиток, значит, клиенту не меньше 21 года». Вам нужно проверить только тех клиентов, которых обязательно нужно проверить, чтобы выяснить, что правило соблюдается.
За первым столиком, который вы видите, сидят четыре человека. Вы видите, что
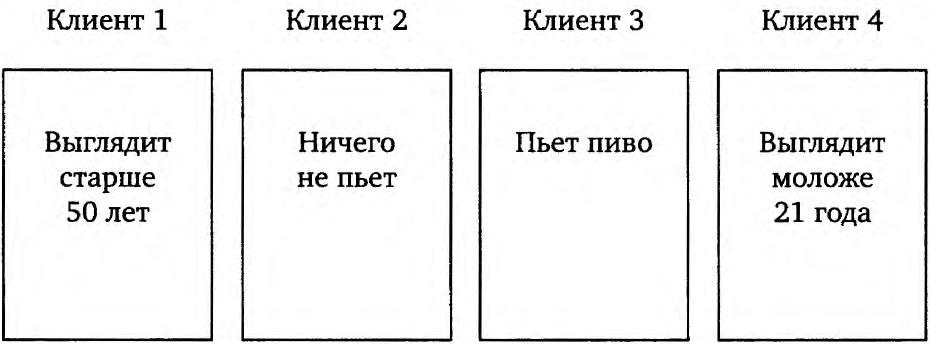
Вам нужно проверить:а) клиента 1;б) клиентов 1, 2, 3 и 4;в) клиентов 3 и 4;г) клиентов 1, 3 и 4;д) клиентов 1 и 3.
Готов поспорить, что вы выбрали вариант в) — клиентов 3 и 4. Теперь вернемся к задаче с карточками. Готов поспорить, что вы не выбрали вариант в), карточка 3 и 4. Теперь вы видите, какое решение было правильным? Логически структура этих двух задач идентична. Давайте проверим мою логику.
ЗАДАЧА С КАРТОЧКАМИНужно убедиться, что соблюдается следующее правило: гласная — значит на другой стороне карточки должно быть четное число.N — не важно, четное ли число на другой стороне карточки.4 — не важно, гласная ли буква на другой стороне карточки.А — должно быть четное число на другой стороне карточки. В противном случае правило нарушается.3 — не должна быть гласная на другой стороне карточки. В противном случае правило нарушается.
ЗАДАЧА ПРО РЕСТОРАННужно убедиться, что соблюдается следующее правило: если человек пьет алкоголь, ему должен исполниться 21 год.Клиент, которому за 50, — не важно, пьет он или нет.Клиент, который не пьет, — не важно, сколько ему лет.Клиент, который пьет, — ему должен исполниться 21 год. В противном случае правило нарушается.Клиент, которому нет 21 года, не должен пить. В противном случае правило нарушается.
Не расстраивайтесь, если вы не справились с задачей с карточками. Абстрактную ее версию смогли решить менее 20% студентов Оксфорда!
Почему задача с карточками оказалась настолько сложнее, чем задача про ресторан? На первый взгляд это может показаться странным, потому что обе задачи решаются с применением условной логики, а именно с помощью простейшего принципа условной логики—правила отделения (modus ponens):
| Если верно П, значит, верно Р. | Если клиент пьет, значит, клиенту 21 год. |
| П верно. | Клиент пьет. |
| Следовательно, Р верно. | Клиенту как минимум 21 год. |
Правило отделения подразумевает правило отрицания (modus tollens). (Если неверно П, значит, неверно Р.) Пример, в котором Р (возраст 21 или больше) не верно, но П (клиент пьет) верно, противоречит условному правилу.
Заметьте, что П (клиент пьет) — это достаточное, но необязательное условие для Р. Достаточно того, что П верно, чтобы Р было тоже верно. Многие другие условия могут быть достаточными, чтобы требовалось, чтобы человеку уже исполнился 21 год. Например, управление самолетом или азартные игры.
В биусловном высказывании, если П верно, этого одновременно достаточно и необходимо, чтобы было верно Р. Сюда входит (довольно странное) правило о том, что, если вы пьете алкогольный напиток, вам уже должен исполниться 21 год, а если вам уже исполнился 21 год, то вы, должно быть, пьете алкогольные напитки.
После того как мы обсудим проблему условного логического мышления, мы вернемся к вопросу о том, почему задачу про алкоголь так легко решить.
Правдоподобие, обоснованность и логика условных высказываний
Как мы увидели, силлогистические доказательства могут быть обоснованными — то есть могут быть верно отражены в форме аргументированного доказательства, — даже если выводы будут неверными. Точно так же дело обстоит и с логикой высказываний.
Решите, какое из следующих доказательств, имеющих по две предпосылки и по одному выводу, является обоснованным.
ДОКАЗАТЕЛЬСТВО А
Условие 1. Если он умер от рака, значит, у него была злокачественная опухоль.
Условие 2. У него была злокачественная опухоль.
---------------------------------
Вывод. Следовательно, он умер от рака.
ДОКАЗАТЕЛЬСТВО Б
Условие 1. Если он умер от рака, значит, у него была злокачественная опухоль.
Условие 2. Он умер не от рака.
---------------------------------
Вывод: Следовательно, у него не было злокачественной опухоли.
ДОКАЗАТЕЛЬСТВО В
Условие 1. Если он умер от рака, значит, у него была злокачественная опухоль.
Условие 2. Он умер от рака.
---------------------------------
Вывод. Следовательно, у него была злокачественная опухоль.
Только доказательство В является обоснованным. Оно согласуется с правилом отделения: если П (умер от рака) верно, тогда верно Р (была опухоль). П (рак) верно. Следовательно, Р (опухоль) верно. Правдоподобность выводов в доказательствах А и Б сбивает нас с толку, заставляя думать, что доказательства обоснованы. Но доказательство А представлено в необоснованной форме: если П (умер от рака), тогда Р (опухоль). Р (опухоль) верно. Следовательно, П (умер от рака). Это называется ошибкой преобразования, потому что форма логического хода мысли ошибочно преобразует предпосылку «если П, тогда Р» в предпосылку «если Р, тогда П». (Если у него была злокачественная опухоль, значит, он умер от рака.) Если бы это было предпосылкой, тогда мы бы действительно считали, что если Р верно, то П также верно. Но это не являлось предпосылкой данного доказательства.
Если мы не контролируем логическую обоснованность своих доказательств, мы постоянно совершаем ошибки преобразования.
ОШИБКА ПРЕОБРАЗОВАНИЯ 1
Если машина не в гараже, значит, Джейн поехала в город.
Дженнифер сказала, что видела Джейн в городе.
Следовательно, машина не в гараже.
Конечно же, Джейн могла добраться до города как-то иначе, не на машине, и в таком случае машина, вероятно, будет в гараже. Эта ошибка совершается из-за дополнительной информации, содержащейся в нашем опыте. Если Джейн редко выбирается куда-то без машины, мы, скорее всего, совершим такую ошибку; если же она иногда ездит на автобусе, а иногда ее подвозит подруга, то вероятность, что мы совершим эту ошибку, меньше.
ОШИБКА ПРЕОБРАЗОВАНИЯ 2
Если у меня грипп, у меня болит горло.
У меня болит горло.
Следовательно, у меня грипп.
Но, конечно же, есть и другие варианты помимо П (гриппа). Например, обычная простуда или ангина. Эту ошибку мы, скорее всего, совершим, если люди вокруг один за другим заболевают именно гриппом, а не чем-либо еще, и при этом у каждого болит горло. Если же люди вокруг в равной степени болеют гриппом, простудой или страдают от аллергии, тогда вероятность, что мы совершим эту ошибку, гораздо меньше.
Выше мы прочитали о доказательстве Б. Если смерть от рака, значит, злокачественная опухоль; если смерть не от рака, следовательно, нет злокачественной опухоли. Это называется инверсная ошибка. Формула этого необоснованного доказательства такова, что если П значит Р; нет П, значит, нет Р. Мы очень часто допускаем такую ошибку.
ИНВЕРСНАЯ ОШИБКА 1
Если идет дождь, то улицы мокрые.
Дождь не идет.
Следовательно, улицы не мокрые.
Если вы живете в городе, где регулярно используются поливальные машины или стоят очень жаркие дни и улицы периодически освежают с помощью пожарных кранов, то вы с меньшей вероятностью допустите эту ошибку. Если же вы живете в сельской местности, где нет ни поливальных машин, ни пожарных кранов, то вероятность, что вы допустите эту ошибку, очень высока.
ИНВЕРСНАЯ ОШИБКА 2
Если президент Обама мусульманин, значит, он не христианин.
Президент Обама не мусульманин.
Следовательно, президент Обама христианин.
Этот вывод был бы верен, если бы в качестве предпосылки из предыдущего опыта мы обладали неявной информацией, что люди могут быть только мусульманами или христианами. Мы этому, конечно, не верим, но можем предположить, что для Обамы это единственная альтернатива; например, если бы единственными религиями, которые Обама когда-либо рассматривал как возможные для себя, были бы мусульманство и христианство.
Что любопытно, инверсные ошибки и ошибки преобразования приводят к выводам, которые не обоснованы только дедуктивно. Понимать это очень важно. (То есть, эти ошибочные выводы логически не следуют из данных предпосылок.) Однако эти выводы могут быть вполне обоснованы индуктивно. (То есть если предпосылки верны, вывод с большой вероятностью может быть верен.) Ведь если у меня болит горло, то вероятность, что у меня грипп, больше, чем если мое горло не болит. Если дождь не идет, то вероятность того, что улицы мокрые, ниже, чем если дождь идет. Правдоподобность этих индуктивных выводов еще больше увеличивает кажущуюся правдоподобность выводов, не обоснованных дедуктивно.
Можно составлять бесконечный список форм доказательств и логических ошибок. Но некоторые ошибки особенно важны и встречаются особенно часто.
Прагматические схемы логического мышления
Абстрактную версию условного высказывания — если П, то Р — трудно применять на практике. На самом деле мы всегда мыслим в соответствии с условной логикой, но редко применяем на практике ее полную абстрактную версию. Вместо этого мы часто используем то, что я называю прагматическими схемами логического мышления, то есть наборы правил, полезных в ситуациях, которые случаются в повседневной жизни. В этой книге приводится множество таких схем. В известном смысле вся книга именно об этом. Некоторые из этих схем напрямую проецируются на условную логику. Например, схема различия между зависимыми и независимыми событиями, а также принцип, согласно которому корреляция не доказывает наличие причинно-следственной связи. Принцип безвозвратных издержек и принцип цены возможности дедуктивно обоснованы и могут быть логически выведены из принципов анализа эффективности затрат. Этим принципам учат, читая курс экономики, хотя и не настолько хорошо, как нужно, потому что обычно на этих лекциях не рассказывают, как применять формальные принципы логического мышления в повседневной жизни.
Некоторые прагматические схемы логического мышления выражаются с помощью условной логики, но им недостает дедуктивной обоснованности, потому что они не могут гарантировать правильный ответ. На самом деле эти схемы связаны вовсе не с истинностью или обоснованностью, а с оценкой правильности действий человека. Этот раздел логики называется деонтической логикой, от греческого deon — должное, правильное. Этот вид логики определяет, какая ситуация требует обязательного выполнения какого-либо действия, какая дает разрешение, какая устанавливает опциональное поведение, что превосходит требования и что должно быть обязательно сделано. Договорные схемы являются разновидностью деонтической схемы и могут применяться для решения ряда задач, связанных с разрешениями и обязательствами.
Деонтическая схема, необходимая для решения задачи про возраст, с которого можно пить алкогольные напитки, называется схемой разрешения. Хотите выпить (П)? Вам нужно быть старше 21 (Р). Вам еще нет 21 (не Р)? Тогда не пейте (не П).
Похожей схемой является схема обязательства. Если вам уже 18 (П), вы должны состоять на учете в военкомате (Р). Если вы еще не состоите на учете в военкомате (не Р), значит, вам еще нет 18 либо вы не выполнили обязательство.
Два года обучения на юридическом факультете заметно улучшает деонтическую логику, но те же два года обучения на философском, психологическом, химическом или медицинском факультетах ничего не изменят в этом виде логического мышления.
Второй тип прагматической схемы логического мышления не имеет ничего общего с условной логикой (или по крайней мере попытки наити что-то общее принесут мало пользы), но применяется в самых разных ситуациях и может быть описан чисто абстрактными терминами. Для использования этих схем требуется логическое мышление, но не логика делает эти схемы эффективными, а, скорее, их свойство проливать свет на проблемы, с которыми человек сталкивается ежедневно. Это относится к статистическим схемам и схемам для научных процессов, таких как рандомизированное устройство управления. Эти концепции входят в курсы статистики и методологии, но далеко не всегда преподавателям удается научить студентов создавать прагматические схемы, которые могут быть полезными в их повседневной жизни. В рамках университетских курсов социальных наук и психологии проходят материал, касающийся практических схем, которые применяются в статистических и методологических схемах для решения повседневных задач, но это, увы, не входит в программу естественно-научного и гуманитарного образования. Другие очень популярные практические схемы логического мышления включают принцип бритвы Оккама, трагедию общественных ресурсов и концепцию эмерджентности, о которой пойдет речь в главе 15.
Наконец, некоторые действенные прагматические схемы создают не абстрактные логические сценарии, а эмпирические правила, которые облегчают решение многих повседневных проблем. К ним относятся, например, фундаментальная ошибка атрибуции; обобщение правила, что действующие лица и сторонние наблюдатели по-разному объясняют поведение; боязнь потерь; предубеждение статус-кво; правило, согласно которому одни архитекторы выбора в целом превосходят других по качеству выбора, который они продвигают; вывод, что материальные стимулы не всегда являются лучшим способом заставить людей изменить свое поведение, и многие другие принципы, упоминаемые в этой книге.
Абстрактные прагматические схемы чрезвычайно эффективны, в то время как ценность чисто логических схем ограничена. Я верю в это, потому что имеется пример высокоразвитой цивилизации Китая, основанной на конфуцианстве, которая никогда не интересовалась формальными логическими построениями. В следующей главе мы поговорим о диалектической традиции этой цивилизации и современных дополнениях к ней.
Выводы
Логика освобождает доказательства от любых привязок к реальной жизни, поэтому доказательство можно осуществить формально, не опираясь на убеждения. Формальная логика, вопреки мнению, которого придерживались просветители на протяжении 26 столетий, не является основой повседневного мышления. Такое мышление изначально приводит к логическим ошибкам.
Верность вывода и его обоснованность — совершенно разные вещи. Вывод, сделанный на основе доказательства, обоснован лишь в том случае, если он логически следует из его предпосылок, а верным он может быть независимо от того, верны ли предпосылки и следует ли он из них логически. Логический вывод необязательно должен прямо следовать из данных предпосылок, но, конечно, степень нашего доверия к нему заметно повышается, если у вывода есть как логические, так и эмпирические основания.
Диаграммы Венна являются выражением силлогистического логического мышления и могут быть очень полезны и даже необходимы при решении категориальных проблем.
Ошибки, допускаемые в дедуктивном логическом мышлении, иногда совершаются потому, что проистекают из доказательств, которые обоснованы только индуктивно. Отчасти по этой причине мы так часто совершаем дедуктивные ошибки.
Прагматические схемы логического мышления являются абстрактными правилами логического мышления, которые часто лежат в основе мыслительной деятельности. Они включают в себя деонтические правила, например схему разрешения и схему обязательства. Они также включают в себя множество индуктивных схем, о которых рассказывается в этой книге и которые используются в статистике, анализе эффективности затрат и суждениях на основе обоснованных научных методов. Прагматические схемы логического мышления не настолько широко распространены, как правила логики, потому что они применяются только в определенных ситуациях, но некоторые из них опираются на основания логики как таковой. Другие, как, например, бритва Оккама и концепция эмерджентности, применяются весьма широко, но не опираются на формальную логику. Есть «схемы», которые являются чисто эмпирическими обобщениями широкого практического применения, как, например, фундаментальная ошибка атрибуции.

