Я сделал поразительное открытие — большой круг на местности в южной Англии, который наводил на многих интригующие вопросы касательно его создания. Каким бы невероятным это ни показалось, но все эти объекты на окружности никак не могли попасть на нее по чистой случайности. Ответ могло дать дальнейшее исследование. Был ли этот круг был создан умышленно, тогда он должен быть современником самых первых объектов. Следовательно, уже в начале III тысячелетия до н. э. в Англии должны были жить передовые люди, способные разместить на местности такую структуру.

Нарисованный на карте круг представлялся мне убедительным, но прежде чем продвинуться дальше, я должен был удостовериться в том, что отмеченные мной объекы не были химерой и что круг действительно существует. Этого можно было добиться более требовательным исследованием в сочетании со сложными математи ческими расчетами.

Карты в масштабе 1: 50 000 идеальны для собирания общих черт местности, но недостаточно подробны, что бы оценить точность круга диаметром в 19,3 километра (12 миль).

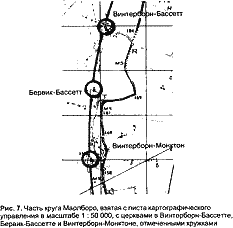
Необходимы карты большего масштаба — от 1: 25 000 до 1: 2500. Хотя окружность круга отмечена рядом церквей и древних земляных сооружений, в центре ее не было явного ориентировочного знака. Мне предстояло изучить различные объекты на местности прежде, чем я мог поверить в то, что — как мне казалось — я открыл.

Карты картографического управления основаны на координатной системе, которая позволяет дать конкретный числовой указатель любой точке на местности в Англии. На картах в масштабе 1: 50 000 такие указатели, или координаты, даются через каждый километр, с подразделением каждого квадрата по 100 метров. Например, координатный указатель церкви в Бервик-Бассетте — 098 735, корректируемый до 100 метров. Самые подробные городские карты картографического управления выполнены в масштабе 1: 1250 и могут показать местоположение объектов с точностью до одного метра. При использовании этой системы письменный стол, за которым я пишу настоящую книгу, может получить точные координаты, по которым любой, пользующийся соответствующей картой картографического управления, может найти его.

Или мое положение может быть определено с помощью всемирных координат широты и долготы, которые обычно используются в навигации и воздухоплавании. Проблема с использованием таких координат заключается в том, что расчеты производятся исходя из сложной геометрии сфер, а она требует использования более сложных уравнений при определении расстояний и угловых соотношений.

Для относительно небольших пространств вроде Британских островов картографы посчитали, что гораздо легче учесть кривизну Земли и установить местную координатную систему, в которой обе сетки координат имеют оди наковую длину. Это облегчает вычисление расстояний и угловых отношений между любыми двумя или тремя объектами. Используемые при этом методы основаны на тригонометрии, которую я изучал еще в школе.

В моем исследовании оказалось весьма важным математическое вычисление на основе координатных указаний картографического управления, ибо позволило мне пользоваться не догадками, а измерениями по масштабным картам. Казалось бы, через ряд точек можно провес ти окружность, но проверить это можно лишь при условии их равного удаления от общего центра. Тригонометрический метод, основанный на указаниях координат, является также наиболее надежным при построении линий через граничащие листы карт. Всем остальным методам не хватает той же точности, даже при очень аккуратных расчетах.

Необходимые математические расчеты не столь сложны, но требуют значительного времени. К счастью, с такими задачами прекрасно справляются компьютеры. Правда, первые мои открытия были сделаны еще до того, как в обиход вошли скромные карманные калькуляторы, так что первоначальные тригонометрические расчеты были сделаны по-старому — с использованием таблиц.

Первым делом следовало установить точные координаты каждого объекта. Для этого я отправился в картографическое управление Великобритании в Саутгемптоне и потрудился в его богатой библиотеке с подробными картами графств в масштабе 1:2500. В этом управлении имеется также картографическая информация по всем археологическим открытиям, сделанным в интересующей нас части Уилтшира.

Изучив карты, я ради упрощения расчетов решил работать с точностью до 10 метров (33 футов). Самая маленькая церквушка имеет по крайней мере 30 метров (98 футов) в длину, а остальные гораздо больше. Исходными ориентирами для церквей я выбрал перекрещение прохода с поперечным нефом, а для мегалитических объектов вроде курганов и других земляных сооружений — то, что считал их центром.

Проблема с Эйвбери заключалась в его размере — его диаметр составляет 421 метр (1381 фут). Окружность моего круга проходила через западный край хенджа, и потому трудно было определить точку отсчета, ибо не было причин предпочесть в расчетах один ориентир другому, и я решил оставить его за скобками.

Установив координаты остальных четырнадцати объектов, я потратил затем массу времени на детальное вычисление центра круга на местности. Для нахождения общего центра всех точек я поначалу выбрал три точки на окружности и затем рассчитал их общий центр. Затем я повторил расчет для других трех точек объектов и т д. Этот метод дал ряд возможных центров, из которых я вывел среднее значение.

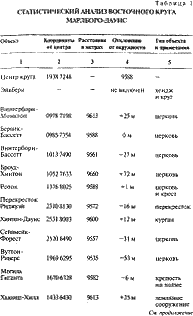
Для абсолютной точности мне следовало провести такие расчеты для всех возможных комбинаций трех объектов. Это потребовало бы тысяч и тысяч вычислений. На практике же и двадцати комбинаций хватило для определения общего центра с достаточной точностью. После вычисления центра я принялся измерять расстояния от него к каждой из четырнадцати точек. Из этих расстояний я вывел средний радиус и величину отклонения каждого объекта от средней линии окружности. (См. таб. 1.)

Средний радиус составил 9588 метров (31 449 футов), или 5,9577 мили. Статистическая ошибка для этой средней величины равна всего лишь 8,07 метра (26 футам), что меньше величины точности координат, которые я брал за основу. Максимальное отклонение от окружности дала церковь в Броуд-Хинтоне, расположенная на расстоянии 72 метров (236 футов) за окружностью, а также церковь в Вуттон-Риверс, расположенная в 53 метрах (174 футах) внутри окружности. Хотя в обоих случаях окружность проходит вне церковных зданий, она все же пересекает принадлежащие им участки, а математические расчеты показывали, что окружность можно провести через пятнадцать объектов, образующих мое первоначаль ное открытие.

Мне еще предстояло определить, было ли это про стым совпадением — при одном шансе из нескольких миллионов — или данный круг был создан умышленно. Я все еще не мог поверить в то, что древние владели искусством, необходимым для создания круга леи радиусом около 9,6 километра (6 миль). По крайней мере, к тому времени я уже знал, что не охочусь за химерами. В моем распоряжении появились убедительные доказательства моей теории.

В следующие несколько выходных я посетил по очереди каждый объект и сфотографировал церкви. Порой можно было видеть древние камни на уровне земли в фундаментах церквей, намекающие на возможность повторного использования гораздо более древних объектов. Я тщательно записывал подробности своих посещений, включая и субъективно ощущавшуюся мною «атмосферу» объектов. Она была почти осязаемой в некоторых местах. Полное описание круглых объектов дано в Приложении 1.

Меловое нагорье Марлборо-Даунг, тут и там отмеченное купами деревьев на могильных холмах, производит внушительное впечатление. Прошлое, кажется, сочится из ландшафта, вызывая ощущение, что что-то глубоко древнее спит в этих холмах. Путешествуя по местности, я был поражен самим размахом предприятия, тех усилий, которых потребовало создание подобного круга.

Меня постигло величайшее разочарование, когда я посетил центр круга, который, по моим расчетам, дол жен находиться в деревне Огборн Сент-Эндрю. В действителыюсти, центр расположен на небольшом поле недалеко от задних садов за несколькими деревенскими домами и от насыпи железной дороги. Поблизости не было сделано значительных археологических находок. Правда, я и нашел могильный холм на церковном дворе в 5-ти метрах (1640 футах) к западу от вычисленной мной точки. Я погрузился в изучение старых археологических карт за интересовавшей меня местности, но так и не смог обнаружить, отмечал ли эту точку какой-либо мегалитический объект или камень. Возможно, эти особенности местности исчезли, когда поблизости прокладывали железную дорогу. Земля из могильного холма или кургана могла стать строительным материалом для насыпи железной дороги.

Плато Марлборо-Даунс вздымается в своей высшей точке до 272 метров (892 футов), из-за чего невозможно обозреть весь круг. Наилучший обзор — с крутого хребта примерно в миле к востоку от центра. Это совпадает с тропой, бывшей когда-то римской дорогой. Отсюда можно четко видеть центр и расположенный от него в 9,6 километра (6 милях) горб продолговатого кургана Ист-Кеннетт, но не видны остальные точки окружности.

Для меня еще оставалось глубокой тайной, как эти конкретные объекты могли быть размещены по окружности такого огромного круга. Мне пришлось обратиться к трудам других исследователей, чтобы открыть уровень мастерства, необходимого для подобной геодезической работы. Затем мне напомнили о труде профессора Александера Тома.

В конце 1950-х и начале 1960-х годов ушедший на пенсию шотландский инженер, профессор Александер Том обследовал более 300 круглых каменных объектов на Британских островах. В 1967 году он опубликовал свои находки в «Мегалитических объектах в Британии». Его книга взбудоражила весь научный мир предположением, что наши древние предки обладали глубоким знанием геометрии, астрономии, топографии и инженерного искусства. В то время археологи уже не могли отрицать невероятные строительные достижения вроде Стоунхенджа, Эивбери и Силбери-Хилл. Но они воспринимались как аномалии, поскольку древние, как известно, вели в то время весьма примитивный образ жизни. Юэн Макки в своей книге «Строители мегалитов» пишет:

На Британских островах повсеместно встречаются каменные круги. Многие из них, к сожалению, были утрачены по прошествии времени, но до сих пор люди открывают новые. Большинство из таких кругов до исследования Тома считались примитивными сооружениями. Многие даже были не совсем круглыми, что вроде бы свидетельствовало о невежестве строителей.

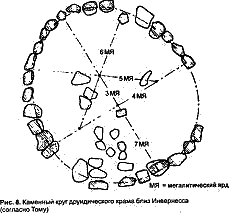
Том же доказал, что круги не только не были неточными, но что их размеры свидетельствовали об использовании сложных геометрических принципов построения овалов и эллипсов. Их планировка неизменно основывалась на треугольниках Пифагора — прямоугольных треугольниках, у которых основание, высота и гипотенуза представляют собой целые числа. Самой известной является пропорция 3:4:5.

Примером может служить друидический храм в виде каменного круга близ Инвернесса в Шотландии (рис. 8). Том указывает, что, построив на земле треугольник 3:4:5, можно создать яйцеобразный круг, используя дуги, выведенные из трех углов треугольника. Это легко сделать с помощью колышков и отрезков веревки или шнура определенной длины. Том считает, что с помощью этого метода строители пытались вывести отношения целых чисел между окружностью и радиусом. По всей Англии он обнаружил множество примеров яйцеобразных или сплющенных кругов вроде замка Ригг в Камбрии (см. рис. 72). Иной раз ему попадались более сложные рисунки, как в случае с Эйвбери-хенджем.

Том также показал, что такие круги часто сориентированы на восход и заход солнца, луны или позицию звезд в определенное время года. И он был не одинок в своем убеждении. В статье, опубликованной в престижном научном журнале «Нейчер» в октябре 1963 года, профессор Джералл Хокинс с помощью компьютерных вычислений установил наличие в Стоунхендже гораздо больше позиций солнца и луны, нежели знаменитый восход солнца в день летнего солнцестояния над Пяточным камнем.

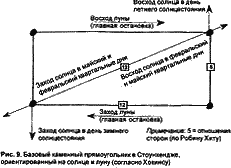
В 1996 году методом радиоуглеродной датировки было установлено, что первый этап строительства Стоуихенджа начался около 2950 года до н. э. Тогда началось сооружение круглого вала и рва и установка четырех ни чем не примечательных камней в форме прямоугольника, известного ныне под не очень-то благозвучным на званием — «Базовый каменный прямоугольник». И все же этот прямоугольник не назовешь обычным. Он был тщательно спланирован таким образом, что прямые линии, проходящие через камни, указывали на восход солнца в день летнего солнцестояния и на заход в день зимнего солнцестояния, а также на восходы и заходы солнца в февральский и майский квартальные дни. Кроме того — что не менее примечательно — он описывал крайние позиции восхода и захода луны в годовом лунном цикле (18,61).

В отличие от Солнца, Луна не кажется движущейся по постоянному пути по небесам при наблюдении с Земли. Точки ее восхода и захода меняются от сезона к сезону и на протяжении цикла в 18,61 года. Этот лунный цикл выделяет крайние позиции восхода и захода луны и именно на них указывает Базовый каменный прямоугольник.

Приглядимся к этим четырем на вид незначительным камням, образующим очень аккуратный прямоугольник, вроде бы и не заслуживающим особого внимания среди других мегалитов Стоунхенджа. Но так уж получается, что только на точно вычисленной широте Стоунхенджа эти четыре знаковых камня, указывающие на упомянутые важные позиции Солнца и Луны, образуют аккуратный прямоугольник. Если сдвинуть его на несколько миль к северу или югу, то прямоугольник превратится в параллелограмм, утратив точную прямоугольную симметрию своих четырех углов. Больше того, прямоугольник основан на другом треугольнике Пифагора с соотноше нием сторон 5:12:13 — примечательный момент, отмеченный Робином Хитом в книге «Ключ к Стоунхенджу».

Итак, перед нами четыре небольших камня, установленные в начале культурного сдвига, произошедшего пять тысячелетий назад, которые многое говорят нам о строителях первой очереди комплекса Стоунхенджа. Они свидетельствуют, что воздвигшие их люди:

1) понимали принципы геометрии, так как смогли построить на местности прямоугольник, используя отношения целых чисел для его сторон и диагонали;

2) тщательно изучили несколько лунных циклов в 18,61 года, то есть имели возможность передавать информацию из поколения в поколение;

3) тщательно изучили места восхода и захода солнца в дни солнцестояний;

4) сумели объединить данные, полученные в пунктах 2) и 3), чтобы вычислить, где им следовало быть, дабы они отвечали критериям, указанным в пункте 1).

Выбранное ими место и стало Стоунхенджем, расположенным к тому же на одной линии, проходящей через крепость на холме Клиэрбери-Ринг, кафедральный собор Солсбери и Олд-Сэрам (см. рис. 2).

Эти факты подразумевают глубокие знания и высокоразвитое математическое, астрономическое и топографическое мастерство — отнюдь не то, что можно было бы отнести к не сложной культуре.

Находки в Стоунхендже подтверждают суждение Тома о том, что создатели мегалитов обладали глубоким знанием геометрии и астрономии. И во многих районах страны имеются убедительные доказательства, что одним из предназначений каменных кругов было наблюдение за небом.

Том выдвинул еще одну поразительную идею — о существовании стандартной единицы измерения, которую он назвал «мегалитическим ярдом» и которая равнялась 2,72 фута, или 0,829 метра. В соотнесении с человеком эта длина приблизительно равна расстоянию от середины груди до основания пальцев, когда рука и ладонь вытянуты в сторону. Следовательно, она могла возникнуть естественным образом, хотя и имеются убедительные признаки того, что эта единица измерения основана на точной пропорции окружности земного экватора.

Признавая точность методики Тома, ряд археологов оспаривают его находки. Будучи правильными, они означали бы, что люди эпохи мегалитов на Британских островах поддерживали общественный порядок на высоком уровне. Находки Тома утверждали бы тогда непрерывность культуры или — иными словами — распространение обеих идей и установленных измерений от Корнуолла на юге до Ирландии на западе и до Оркни и Шетланда на севере. Логические концепции и сведения должны были бы передаваться из поколения в поколение, чтобы их можно было суммировать и уточнить. Обычно это достигалось с помощью письма, являющегося признаком всех известных развитых обществ. Однако нет данных о существовании письменности в ту эпоху.

Такая преемственность могла быть достигнута только в относительно мирном и стабильном обществе. Но это противоречит археологическим находкам. Проводившиеся в течение многих лет тщательные раскопки и исследования создали картину бурного и нестабильного полуварварского существования.

Данные же, полученные Александером Томом при исследовании каменных кругов, и компьютерный анализ Джералда Хокинса согласуются с моим открытием кругового ландшафтного рисунка. Совершенно очевидно, что круг как геометрическая фигура был неотъемлемой частью культуры, существовавшей в Англии около 3000 года до н. э. Изощренность Стоунхенджа указывает на существование народа с передовыми представлениями об астрономии, геометрии и инженерном искусстве. Мог ли тот же народ проявить изобретательность, необходимую для производства съемки и создания круговой схемы в Марлборо-Даунс?

Дабы объединить все эти концепции в одном контексте, необходимо рассмотреть все, что известно об обитателях Британских островов в период позднего неолита и начала бронзового века и об их связях с другими культурами в различных частях света.