Книга: Мистерия пирамид. Тайна Сфинкса.
Назад: ГЛАВА ШЕСТАЯ НАБЛЮДАЯ ЗА НЕБЕСАМИ
Дальше: ЧАСТЬ ТРЕТЬЯ КОД, КОТОРЫЙ НЕОБХОДИМО ВЗЛОМАТЬ
ГЛАВА СЕДЬМАЯ
ЗЕМЛЯ И ГРАНИЦЫ ВРЕМЕН ГОДА
Оставшись сиротой в возрасте двух лет, Мозес Котсуорт (1859—1943) первые понятия об измерении времени получил от своих деда и бабки, а также прадеда и прабабки, которые воспитывали его. Не доверяя вновь изобретенным механическим методам отсчета времени, родственники Котсуорта отсчитывали свое время по солнечным и песочным часам, а также фазам луны, и крайне заинтриговали своего юного отпрыска семейной коллекцией старинных календарей. Котсуорт использовал традиционный интерес своих предков к исчислению времени в собственной карьере одного из руководителей Британских железных дорог. Его математический талант и тяга к числам побудили его в начале 1890-х годов пересмотреть тарифы и расписания следования поездов, а впоследствии усовершенствовать систему статистики железных дорог.
В процессе работы Котсуорт столкнулся с частыми жалобами кондукторов и управляющих на колебания доходов и затрат в разные сезоны года. Однако в таких колебаниях был виновен не Котсуорт, а календарь. В месяцах может быть 28, 29, 30 и 31 день; к тому же в них нет никакой связи между числами и днями недели. Так, например, первое число в одном месяце может прийтись на субботу, а в следующем - на вторник Пытаясь найти более оптимальный способ согласования времени с нуждами статистики и коммерции, Котсуорт последовал примеру Чарльза Пьяцци Смита и занялся изучением вероятности того, что Великая пирамида могла служить идеальным календарем для определения времен года.
С детских лет хорошо зная солнечные часы и понятие истинного полудня, Котсуорт начал свои исследования с создания макетов конусов и пирамид, чтобы понаблюдать, какие тени они отбрасывают при разных углах падения на них лучей солнца. Он выяснил, что на широте Великой пирамиды, составляющей практически ровно 30°, обыкновенный обелиск, выступающий в роли стрелки гигантских солнечных часов, может очень точно указывать время дня. Правда, он должен иметь колоссальные размеры - примерно 450 футов (ок 140 м), чтобы отбрасывать тень, длина которой ежедневно, в зависимости от конкретного времени года, изменялась бы достаточно значительно (примерно на 1 фут (30 см) в день). Это позволило бы определять и время года, и его продолжительность. Особенно удобна пирамида для определения времен (сезонов) года. Ее северная сторона на протяжении шести зимних месяцев оставалась бы в тени. Затем, по мере приближения солнца к зимнему солнцестоянию, ее тень становилась бы все более и более длинной, а затем начала бы сокращаться, достигнув своего минимума в день весеннего солнцестояния, в конце марта. Чтобы эту тень можно было замерить, рассуждал Котсуорт, строителям пирамиды была необходима ровная площадка с северной стороны монумента, имевшая нечто вроде геометрической разметки, позволявшей им отмечать ежедневное продвижение тени. И вот в ноябре 1900 года Котсуорт отправился в Египет, чтобы на месте проверить обоснованность своих гипотез.
И он действительно нашел такой объект - сооружение из плоских блоков, образующее полуквадраты, которые простираются от платформы Великой пирамиды до остатков древней стены, некогда окружавшей весь комплекс Хуфу. Ширина каждого камня составляла 4,45 фута (1,36 м) - расстояние, которое тень проходит каждый день по мере приближения к точке исчезновения в марте. Эта каменная «шкала» позволяла жрецам комплекса пирамиды с особой точностью исчислять дни зимней половины года и путем математических манипуляций определять месяц и день года.
Котсуорт уехал из Египта, увозя с собой проект своего 13-месячного календаря, продолжительность месяцев в котором составляла 28 дней, причем месяцы всегда начинались в воскресенье, а завершались в субботу. Котсуорт заручился поддержкой Джорджа Истмена, основателя компании «Истмен Кодак», производившей фотокамеры. Истмен был убежден, что неудачный календарь оборачивается для бизнесменов громадными убытками. Его интерес к новому календарю, как и у Котсуорта, был чисто практическим, а никак не религиозным или мифологическим. Статистик Британских железных дорог прекрасно понимал, что более точный календарь способен принести громадную пользу людям, жизнь которых зависела от смены сезонов, показывая им время разливов Нила и начала сельскохозяйственных работ. Но чтобы доказать, что Великая пирамида могла использоваться не только для определения момента смены сезонов, но и для геодезической съемки земель после каждого ежегодного разлива Нила, нужен был другой праюичный человек.
Бригада геодезистов эпохи Древнего царства
Однажды - дело происходило в конце XIX века - Роберт Т. Баллард, австралиец по происхождению, сидя в вагоне поезда, медленно миновавшего плато в Гизе, взглянул на три главных пирамиды и заметил нечто странное. Поскольку монументы четко вырисовывались на фоне неба, а угол обзора по мере движения поезда постоянно менялся, Баллард подумал, что пирамиды вполне могли служить древним в качестве приборов - теодолитов, если говорить на языке геодезистов - для геодезической съемки и триангуляции.
Инженер-железнодорожник по профессии, Баллард был знаком с основами прокладки маршрутов и определения прямых линий. Он понимал, что определение границ земельных владений представляло серьезную проблему на берегах Нила, особенно в Нижнем Египте, где ежегодные разливы затапливали земли на огромных пространствах, смывая практически все межевые знаки между имениями землевладельцев. Поэтому ежегодное восстановление межевых знаков имело крайне важное значение, и пирамиды существенно облегчали эту задачу. Единственным инструментом, который, как писал Баллард в своей книге, изданной в 1882 году и гордо озаглавленной «Решение загадки пирамид», был необходим древним геодезистам, являлась переносная модель Великой пирамиды в центре круглой доски-панели с указанием сторон света. Египтянам оставалось только направить северную метку доски на север, сориентировать модель пирамиды так, чтобы на ней было то же распределение света и тени, что и на реальной пирамиде, и - прочесть показания. Это было совсем нетрудно. Балларду стало ясно, что пирамиды постоянно использовались для того, чем геодезисты занимаются постоянно: для измерений площади земель при посредстве метода целых треугольников с отношением сторон 3—4—5.
Гипотеза Балларда подтверждает точность свидетельств Геродота в его записках о Египте. Страна в древности была густо заселена на плодородных землях Нильской долины. По некоторым оценкам, плотность населения составляла примерно 700 человек на квадратную милю. Чтобы поддерживать мир и справедливость, писал Геродот, «этот царь разделил землю... так, чтобы каждому досталось по четырехугольнику одинаковой величины... и на всех наложил подать. Но ко всем, от чьего надела река смыла хоть небольшую часть... он послал надсмотрщиков, чтобы проверить, насколько меньше стала его земля, чтобы тот владелец платил подать только за ту землю, которая у него осталась. Таким образом, мне кажется, произошла геометрия, которая оттуда была занесена в Грецию».
Геродот и Баллард признали, что геометрия - слово, заимствованное из греческого и означающее «землемерие», - возникла не из абстрактной математики, а из таких будничных, повседневных потребностей, как определение границы, у которой кончается надел одного владельца и начинается имение другого. Важный аспект, о котором Баллард не упомянул, а Геродот, возможно, имел в виду, - это то, что подобные ежегодные упражнения в геометрии со временем обрели религиозное значение. Каждый год разлив Нила и затопление огромных территорий как бы напоминали о возврате хаоса водной стихии - хаоса, из которого возник космос, представлявшийся в виде холма творения. На этом холме-космосе предстояло установить порядок и справедливость, то есть совершенный ма’ат. Геометрия помогала возродить порядок, нарушенный наводнением, и вернуть вселенной утраченную гармонию и равновесие сил. Таким образом, геометрия восстанавливала на земле ту самую гармонию, которую фараон стремился установить среди своих подданных.
Одно из названий, данных египтянами своей родной земле, звучало как То-Мера, что означало «земля мр». Слово мр первоначально обозначало средний треугольник пирамиды и в более широком значении - саму пирамиду. Таким образом, коренной смысл этого древнего названия заключается в том, что Египет был измеренной землей, особым районом на планете, известным своей уникально точной геометрией. Люди эпохи Древнего царства знали топографию Обоих Египтов во всех деталях и, естественно, воплотили свои обширные познания в возведении Великой пирамиды.
Две измеренных страны: Два Египта
Как мы увидим ниже, Великая пирамида свидетельствует, что древним египтянам было известно, что Земля - круглая. Если бы мы, подобно людям XV века, выросли на исторической легенде о плавании отважного Колумба на трех крошечных каравеллах на запад, туда, где плоская Земля круто обрывается в космическую пропасть, это утверждение показалось бы нам почти невероятной фантазией о высоте интеллектуальных достижений обитателей Древнего мира. По сути дела, легенда о Колумбе и плоской Земле говорит нам скорее об отсталости Европы XV века, чем о седой древности. Жители Древнего Египта прекрасно знали, что Земля отнюдь не плоская, и по меньшей мере за 40 веков до Колумба имели достаточно мужества, чтобы посвятить свою жизнь подтверждении этой гипотезы.
Можно лишь удивляться, почему европейцам так долго не хватало смелости признать, что Земля - круглая, ибо многие образованные люди на протяжении обозримой истории пот нимали, что Земля имеет форму сферы. Взгляните на Луну во время полнолуния и спросите себя: «С какой стати Земля должна иметь другую форму?» Понаблюдайте за кораблем, приближающимся к горизонту, и вы увидите, что его корпус перестанет быть видимым задолго до того, как исчезнет верхушка последнего радара на верхней рубке. Звезды также указывают на сферичность Земли. Если вы отправитесь строго на север из любой точки Северного полушария, на небе непременно покажется северный небесный полюс, а с ним и все звезды, появляющиеся на ночном небе. Поверните на юг - и они исчезнут. Это наблюдение требует пояснений.
Во-первых, древние египтяне не боялись упорной кропотливой работы. Как свидетельствует комплекс в Набта-Плайя, они были опытными наблюдателями звездного неба по меньшей мере за несколько тысячелетий до начала эпохи Древнего царства. Они жили в стране, простирающейся с севера на юг. Звезды, восходившие над горизонтом в Верхнем Египте (на юге), казались более высокими в Нижнем Египте (на севере). Египтяне обратили внимание на эту разницу и использовали ее в своих наблюдениях.
Они учитывали ее и при выборе площадки для Великой пирамиды или, не исключено, каких-то более древних и еще не открытых сооружений, предшествовавших ей. Великая пирамида стоит почти точно на 30° северной широты. Слово «почти» употреблено здесь потому, что на самом деле она находится чуть к югу от этого меридиана. Почему это именно так - установил Ричард Проктор в процессе своих исследований астрономического использования Великой пирамиды. Если двигаться постоянно на север от экватора, на небесах появится северный полюс небесной сферы и будет подниматься до тех пор, пока на Северном полюсе он не окажется прямо над головой. Оказывается, широту достаточно легко измерять путем определения угла положения северного полюса небесной сферы над горизонтом. Если северный полюс небесной сферы находится на высоте 30° над горизонтом. Между тем это не совсем так, ибо при этом не учитывается атмосферная рефракция. Когда вы глядите на горизонт, вы смотрите через более плотную атмосферу, чем когда смотрите прямо перед собой. В связи с этой незначительной рефракцией наблюдение угла северного полюса небесной сферы дает неизбежную погрешность, которая уменьшается при приближении от экватора к полюсу. На меридиане 30° северной широты вам кажется, что вы продвинулись к северу чуть дальше, чем на самом деле. С другой стороны, Проктор доказал, что, если для определения широты вы используете солнце и тень без учета атмосферных эффектов, вам будет казаться, что вы находитесь значительно южнее относительно своего реального положения. Великая пирамида находится на расстоянии примерно 2,2 км к югу от линии прохождения 30° северной широты. Проктор считает этот факт бесспорным аргументом в пользу того, что древние египтяне использовали околополярные звезды для определения своего положения относительно оси север-юг на земной сфере.
Но поскольку египтяне знали, что Земля имеет форму сферы и знали свое местонахождение на ней, они, несомненно, задавались вопросом: каковы размеры Земли?
Теоретически ответить на это вопрос не так уж сложно. Прежде всего надо устроить астрономические обсерватории на разных широтах. В идеале эти обсерватории должны располагаться строго к югу и к северу друг от друга, но в точном математическом анализе можно использовать и данные, полученные и при менее точной ориентации обсерваторий. Затем надо выбрать какую-то одну звезду и определить угол ее апогея из каждой обсерватории. В качестве альтернативы можно измерять угол положения Солнца в полдень в определенных точках годового цикла, например, в день равноденствия или солнцестояния. Простые геометрические расчеты показывают, что разница между показаниями измерений зависит от разницы положения обсерваторий на разных широтах. Теперь надо перепроверить эти измерения в отношении других звезд или точек солнцестояния и равноденствия. Третий этап - это измерение географического расстояния между двумя наземными обсерваториями. На основании этих данных можно определить географическое расстояние, эквивалентное изменению широты на Г. Наконец, остается умножить расстояние, соответствующее Г, на 360 - число градусов в окружности. В итоге получим длину окружности Земли через точки полюсов.
Обычно история науки приписывает честь первого измерения длины окружности Земли грекоязычному астроному Эратосфену, выполнившему эти расчеты ок. 250 г. до н.э., спустя более чем два тысячелетия после IV династии и великой эпохи строительства пирамид. Эратосфен проводил свои расчеты в Египте, используя углы положения Солнца в день летнего солнцестояния в г. Александрия на побережье Средиземного моря и в Сиене на Ниле в Верхнем Египте. В итоге он получил цифру 250 000 стадий - величина весьма проблематичная, поскольку точная длина 1 стадии неизвестна. Согласно классическому определению, 1 стадия равна 1/10 мили, так что, по расчетам Эратосфена, длина окружности земного шара составляет 25 000 миль. Это почти на 200 миль отличается от современных замеров, то есть погрешность составляет менее 1 %.
Учитывая все, что нам известно о древнеегипетской астрономии и математике, нет никаких сомнений, что представители элит Додинастического периода и эпохи Древнего царства обладали всем необходимым для измерения длины окружности Земли. Но сказать, что египтяне могли сделать это, - далеко не то же самое, что доказать, что они действительно осуществляли это. Представители официальной египтологии давно отвергли гипотезу о том, что древние египтяне не были примитивным народом, едва способным решать простейшие арифметические задачи. И это - несмотря на выдающиеся архитектурные творения, оставленные нам египтянами. Однако существует и другая, не менее упорная традиция, гласящая, что египтяне обладали высокими познаниями и увековечили их в Великой пирамиде. Подобная логика рассуждений возникла уже в недавнее время благодаря смелому и предприимчивому французу по имени Жан-Франсуа Жомар (1777—1862). Жомару едва перевалило за двадцать, когда он сопровождал Наполеона в качестве одного из савантов (ученых), присутствие которых превратило его военную экспедицию в Египет в крупнейшее событие в интеллектуальной истории Запада -событие, итогом которого явилось создание громадного, многотомного, написанного многими авторами труда «Описание Египта».
Одной из задач, которую было поручено выполнять Жомару во время наполеоновской агрессии, было проведение обмеров Великой пирамиды. Это была трудная задача, поскольку вокруг монумента громоздились целые горы обломков и мусора. Однако, выполнив промеры, Жомар и его коллеги выяснили, что длина стороны монумента составляла 230,9 м, или 757,5 фута. Затем Жомар поднялся на вершину пирамиды и, спускаясь вниз, промерил высоту каждой ступени. В итоге у него получилось, что высота пирамиды составляет 144 м, или 481 фут. С помощью тригонометрических функций Жомар вычислил, что угол Великой пирамиды составляет чуть более 5 Г, или, точнее, 51° 19' 14". Другая серия расчетов позволила Жомару определить апофему -расстояние от вершины пирамиды до середины любой из ее сторон; эта величина составила 184,722 м. В силу необходимости Жомар был вынужден прибегать к округлениям. Поскольку внешний ряд облицовки пирамиды отсутствовал, Жомару пришлось сперва вычислить гипотетическую толщину известняковых плит и уже затем использовать эту величину в дальнейших расчетах.
Полученный Жомаром результат - 184,722 м (или 606 футов) - произвел сильное впечатление на юного француза, воспитанного на трудах классиков. Он помнил, что античные историки и географы Диодор Сицилик (Сицилийский) (ок. 80—20 гг. до н.э.) и Страбон (ок. 63 г. до н.э. — 24 г. н.э.) утверждали, что апофема Великой пирамиды равна примерно 1 стадии, или 600 футам, что было основной единицей измерения длины в Античном мире. Александрийские греки, члены той же обширной эллинистической общины, в которой выросли Гиппарх, официальный первооткрыватель прецессии, и Эратосфен, считали, что 1 стадия равна 185,5 м (606,8 фута) - величина, поразительно близкая к собственным замерам апофемы пирамиды, выполненным Жомаром. Было ли это простым совпадением или же строители пирамиды сделали это сознательно?
Некоторые из коллег Жомара поддерживали его гипотезу о геодезическом назначении пирамиды. Когда геодезисты, бывшие в числе савантов Наполеона, убедились, что монумент удивительно точно сориентирован по четырем сторонам света, они использовали линию меридиана север - юг, проходящую через вершину Великой пирамиды, в качестве базовой линии отсчета в своих обмерах территории страны.
Это привело к удивительному открытию: меридиан, проходящий через вершину, делил Нижний Египет на две совершенно одинаковые половины, а диагонали, проведенные через углы Великой пирамиды, полностью накрывали собой дельту Нила.
Однако другие коллеги Жомара встретили его идеи в штыки. Перемерив длину основания пирамиды, они получили величину на 2 м больше, чем в замерах Жомара. Кроме того, другой получилась у них и высота. Определенная ими цифра была выше, чем у Жомара, в результате чего угол наклона у него получился слишком низким, а апофема - слишком короткой. Таким образом, та точность, которой так кичился Жомар, обернулась натяжками и грубыми приближениями.
Жомар, однако, не сдавался. Он утверждал, что Понижающийся коридор представлял собой древнюю обсерваторию для наблюдений за околополярными звездами - гипотеза, как мы уже знаем, имеющая под собой серьезные основания, - и что объект, находившийся в камере Фараона, представлял собой не саркофаг, а сейф для единицы мер, нечто вроде эталона метра эпохи Древнего царства.
Однако современные египтологи отвергают большинство гипотез Жомара о знаниях древних египтян о Земле, считая их попыткой выдать желаемое за действительное. И лишь во второй половине XX в. ряд любопытных эзотерических исследований показал, что Жомар был во многом прав.
Особая важность локтя
Покойный Ливио Сатулло Стеччини сделал карьеру, которую сами академики считают эталоном академизма. Сын профессора права из университета в г. Катанья (Италия), Стеччини в колледже изучал латынь и древнегреческий, а затем философию во Фрейбургском университете, где читал лекции выдающийся философ-экзистенциалист Мартин Хайдеггер (1889—1976). Стеччини, однако, интересовала не столько философская трактовка природы бытия, сколько изучение древних единиц измерений - тема, которая впервые увлекла его уже в годы учебы в университете. Вынужденный покинуть Германию в результате нападок гитлеровских идеологов на преподавание астрономии в университетах, Стеччини вернулся в Италию, получил ученую степень доктора римского права и занял кафедру в Римском университете. Вторая мировая война вынудила Стеччини перебраться в Соединенные Штаты, где он выдвигался на соискание второй докторской степени в Гарвардском университете, на этот раз - по античной истории. Хотя его профессора более всего любили древних греков за их великие творения в области литературы и философии, Стеччини более всего влекло изучение утилитарных и практических аспектов их жизни. Темой своей диссертации он выбрал происхождение монет и денежного обращения в Греции. Его работа встретила положительный отклик, и Стеччини была присуждена докторская степень, но специалисты Гарвардского университета предложили ему убрать все цифры из рукописи перед тем, как публиковать ее, поскольку профессора-классики в то время не проявляли интереса к тому, что казалось им нагромождением непонятных арифметических выкладок
Стеччини же любил числа, особенно - древние единицы мер, и продолжал свои исследования мер Древнего мира. От изучения веса греческих монет он перешел к исследованию деятельности монетных дворов Греции, размеров греческих храмов и, наконец, к географии и геодезии Древнего мира. В конце концов его коллеги-академисты заявили ему, что в исследованиях античности цифры не являются доказательствами. Оскорбленный Стеччини подал в отставку, проигнорировав их советы и предпочтя работать, как он называл это, в «блистательной изоляции».
На деле же одинокий труд Стеччини продемонстрировал, что цифры являются доказательствами. Особенно - во всем, что касается Великой пирамиды.
Французские геодезисты из числа савантов, как доказал Стеччини, обнаружили лишь самые начатки умения древних египтян проводить точные измерения земель, на которых они жили. Геодезисты были правы, определив, что меридиан, проходящий через вершину Великой пирамиды, делит регион Нильской дельты пополам. На деле эта линия служила в качестве первого меридиана для всего Египта. Египтяне проводили его от города Бехдет, столицы Египта Додинастического периода, находившейся вблизи от места, где Нил впадает в Средиземное море, в точке ЗГ 30' северной широты, до Большого порога на Ниле, лежащего южнее на той же самой долготе. Южная граница Египта проходила по линии 24° 00' северной широты, неподалеку от точки, где Нил пересекает тропик Рака, лежащий на линии 23° 5 Г северной широты (с тех пор он несколько сместился), вблизи от Первого порога на Ниле возле Асуана.
Восточная и западная границы страны проходят по оси север - юг от границ Нильской дельты вдоль линий, параллельных первому меридиану. В результате страна имела форму длинного, сильно вытянутого прямоугольного треугольника.
Геодезические знания в Древнем Египте были настолько «совершенными», что первый меридиан страны служил ориентиром не только для городов и храмов в самом Египте, но и для всего остального восточного Средиземноморья. В Древнем Риме он служил для той же цели - ориентации на земле, для которой в наши дни служит линия 0° долготы - знаменитый Гринвичский меридиан (Англия). Гора Герицим, раннеев-рейское священное место, а впоследствии - ритуальный центр секты самаритян (самарян), находится ровно в 4° к востоку от первого египетского меридиана. Дельфы, один из двух центров оракулов классической Греции и важнейший с точки зрения геодезии центр древних эллинов, расположен на расстоянии ровно 7° к северу от г. Бехдет на той же линии долготы, что и первый египетский меридиан, тогда как Мекка, главный священный центр ислама (хотя сами объекты Мекки восходят к гораздо более древней, доисламской культуре), лежит на расстоянии ровно 10° к востоку от западной границы Египта и 10° к югу от г. Бехдет. Таким образом, Египет являл собой средоточие Древнего мира.
Геодезическая система Древнего Египта свидетельствовала о тесной унификации мер в Обоих Египтах. В Додинастический период египтяне считали, что расстояние между северной границей страны (которой считался Бехдет, лежавший на 31° 30' северной широты) и южной границей (проходившей по 24° 00' северной широты) составляет 1,8 млн. географических локтей. Таким образом, один географический локоть был равен примерно 1,5 современного фута, или, точнее, 461,7 мм. Локоть, графическим знаком которого служило изображение руки до локтя (фонетически транслитерируемого как «mh» («мх»),был основной единицей длины не только в Древнем Египте. Само понятие локоть (перевод римского cubitum с тем же значением) - мера очень древняя. Один локоть делился на 6 ладоней, каждая из которых, в свою очередь, состояла из 4 пальцев. После унификации системы мер в Египте распространение получила вторая геодезическая система, измерявшая расстояние от основания Нильской дельты (в точке 31° 30' северной широты) до южной границы Египта (24° 00' северной широты) как равное 1,5 млн. географических локтей. В этой новой системе мер один локоть, так называемый царский локоть, составлял 524,1483 мм (или ок. 20,6 современного дюйма, то есть почти 1,72 современного фута). Такой более длинный царский локоть состоял из 7 ладоней в каждом, а в каждой ладони насчитывалось 4 пальца.
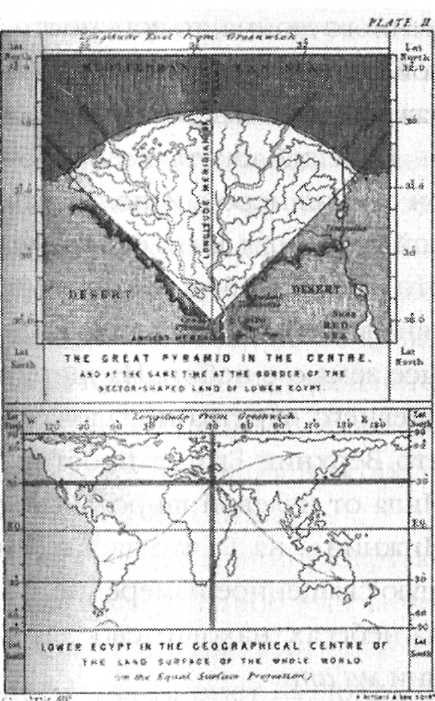
Положение Гизы и Великой пирамиды относительно Нильской дельты и планеты Земля в целом.
Царский локоть имел особо важное значение, поскольку он служил мерой, использовавшейся при возведении Великой пирамиды. В его основе лежали семь составных единиц, что имело особую важность, ибо число 7 считалось у египтян священным как число космического плана, объединяющее землю с небом. Например, для жителей Египта эпохи Древнего царства немаловажное значение имел тот факт, что Верхний Египет простирался на 6° вверх по течению Нила от нулевой широты (широты Великой пирамиды), а Нижний - на 1°, что дает в сумме 7° - величину, отражающую священное измерение. Священная гармония, царящая на небесах, находит свое выражение в видимом воплощении ма'ат.
Египтяне также использовали аспект небесного измерения в том, как они проводили границу между Верхним и Нижним Египтами, что помогает понять мотивы ориентации Великой пирамиды. В эпоху Древнего царства южная граница Египта рассматривалась не как одна линия, но как сложносоставная единица из трех линий. Самая южная точка тропика Рака -23° 51'. Когда солнце поднимается в зенит в полдень в точке летнего солнцестояния, оно находится в точке 24° 6', что является и широтой нижней границы Первого порога на Ниле. Это - самая северная из трех «граничных линий». А между ними находится линия 24° северной широты - широты верхней границы Первого порога.
Исходя из соображений космической симметрии, египтяне продублировали эту систему на границе Верхнего и Нижнего Египтов. Они создали три граничных линии, каждая из которых отстояла на 6° от соответствующей южной границы: 30° 6', 30° и 29° 5 Г. Показательно, что полоса земель между 30° 6' и 29° 5 Г не находилась в юрисдикции ни одного из округов, или номов, ни Верхнего, ни Нижнего Египта. Эта граничная зона представляла собой нечто вроде Федерального округа Колумбия в США или Федерального округа Мехико - общенациональной столицы, на территорию которой не распространяется юрисдикция ни городских, ни федеральных законов, ни законов штата.
Иероглифические знаки изображают границу округа-нома в качестве прямоугольника, который либо пуст внутри, либо окружает воду или рыбу. Этот образ или «икона», встречающиеся по всему миру, символизируют Квадрат Пегаса, созвездие из четырех звезд, имеющих форму квадрата. Эти звезды ассоциируются с водой и рыбой, поскольку они являются частью зодиакального созвездия Рыб (Pisces по-латыни). В древние времена Квадрат Пегаса служил исходной точкой для составления карты звездного неба. Египетский символ нома - «водоем с рыбой» - занимал то же место на карте Земли и служил центром Обоих Египтов.
Не случайно Великая пирамида находится в центре этого нома, на 30° северной широты или, во всяком случае, предельно близко от нее, насколько это могли определить древние египтяне. Все сооружение занимает собой условную точку равновесия между Верхним и Нижним Египтом, располагаясь точно на меридиане, а его углы и диагонали, проведенные из них, определяют форму нильской дельты, а также границы Египта. Любое из этих соответствий могло возникнуть случайно, но такое их обилие в одной точке -это уже не совпадение.
В этой связи не следует думать, будто египтяне эпохи Древнего царства страдали эгоистическим нарциссизмом. В конце концов, они считали свою страну отправной точкой составления карты Земли точно так же, как Квадрат Пегаса выполнял ту же функцию в небе, и воспринимали свой меридиан в качестве центра Древнего мира. Но при этом египтяне устремляли взор и за пределы своей страны. По словам Стеччини, они выразили в пропорциях Великой пирамиды точную модель Северного полушария.
Модель эта начинается с подсчета периметра Великой пирамиды. Согласно замерам суммарной длины всех ее сторон, полученным Д.Коулом в 1925 г., периметр монумента составляет 921,455 м. Эта величина практически точно соответствует величине S' широты на экваторе: 921,463 м. А если египтяне эпохи Древнего царства знали, что S' на экваторе составляет 1758 царских локтей, и использовали эту величину в своих расчетах, это означает, что они знали и истинную длину окружности Земли.
На самом деле их познания простирались еще дальше. Они знали, что Земля - это не круглая сфера, а сплюснутый сфероид. Радиус, проведенный от центра планеты до экватора, немного длиннее и равен 6 378 758 м, чем радиус, идущий от центра до любого из ее полюсов, составляя б 355 858 м, по тем же подсчетам. Таким образом, разница составляет 22 900 м. Ключ к этой величине - высота самой Великой пирамиды, составляющая 280 локтей. Это число вызывало у древних египтян космические ассоциации, ибо 28 без остатка делится на 7. Однако, утверждает Стеччини, Великая пирамида на самом деле капельку «не дотягивает» до этой высоты, составляя 279,5 локтя. Отняв пол-локтя от целой и кратной величины, египтяне тем самым косвенно указывали на слегка сплюснутую форму Земли на полюсах. Они знали, что длина окружности линии широты на экваторе длиннее, чем возле полюсов (см. Приложения и, в частности, раздел, озаглавленный «Широта и приплюснутость на полюсах, выраженные в пропорциях Великой пирамиды»).
Еще в начальной школе мы знакомимся с так называемой проекцией Меркатора - картой, которая пытается передать сферическую форму Земли, превратив ее в плоский прямоугольник. Древние египтяне делали примерно то же самое в отношение Великой пирамиды. Они проецировали параметры Северного полушария на четыре треугольника, вершины которых соответствовали полюсу, а периметр -экватору. Масштаб при этом составлял 1:43 200; это число было выбрано потому, что оно соответствует длительности половины дня (1 день = 24 часам = 1440 минутам = 86400 секундам; 86 400 : 2 = 43 200).
В середине III тысячелетия до н.э. древние египтяне на деле показали, что обладают такими знаниями о форме нашей планеты, которые оставались неизвестными вплоть до XVII века и работ Исаака Ньютона, а экспериментально были подтверждены лишь в XVIII веке.
Числа и знания
Совершенно ясно, что ко времени Древнего царства египтяне обладали детальными знаниями о форме Земли и весьма преуспели в деле закладки этих знаний в пропорциях Великой пирамиды. С их точки зрения, эти знания вовсе не были чем-то новым. Геодезическая реформа, которая сопровождала объединение Обоих Египтов и в итоге которой царский локоть, основанный на семи ладонях, заменил собой географический локоть, указывает на совокупность познаний, сложившихся задолго до того, как Мен превратил разобщенные номы в единое политическое целое. Астрономические познания древних египтян восходят по меньшей мере ко временам звездочетов эпохи Набта-Плайя.
Великая пирамида высится над пустыней словно напоминание о масштабе и древности этих знаний как о земле, так и о небесах, предлагая нам хотя бы самый общий контур этих знаний. Это само по себе достаточно, но возникает вопрос: неужели существует еще что-то, что они хотели поведать нам?

