7
Происхождение массы
Открытие формулы E = mc2 стало переломным моментом в представлениях физиков об энергии, поскольку этот закон помог понять, что существует огромный запас потенциальной энергии, которая замкнута внутри самой массы. Этот запас энергии гораздо больше, чем кто бы то ни было может себе представить: заключенная в массе протона энергия почти в миллиард раз превышает высвобождаемую в процессе обычной химической реакции. На первый взгляд может показаться, что мы нашли решение энергетических проблем нашей планеты, причем вполне действенное в долгосрочной перспективе. Однако в этой бочке меда есть ложка дегтя, и довольно большая: полное разрушение массы сопряжено с серьезными трудностями. В случае атомной электростанции, использующей принцип ядерного распада, разрушается совсем незначительная часть исходного топлива. Остальная часть топлива превращается в более легкие элементы, часть которых может представлять собой в высшей степени токсичные отходы. Даже в недрах Солнца процесс ядерного синтеза протекает крайне неэффективно с точки зрения преобразования массы в энергию, и происходит это не только потому, что доля превращаемой массы очень мала: у любого отдельного взятого протона крайне мало шансов вступить в синтез, поскольку первый шаг процесса превращения протона в нейтрон — весьма редкое событие. На самом деле это бывает настолько редко, что требуется в среднем около 5 миллиардов лет, чтобы в сердце звезды произошло слияние одного протона с другим, что приводит к образованию дейтрона и запускает процесс выделения энергии. Фактически это вообще было бы исключено, если бы на таких малых расстояниях не доминировала квантовая теория: согласно доквантовой картине мира Солнце просто недостаточно горячее для того, чтобы в нужной степени приблизить протоны для их слияния. Для этого его температура должна быть примерно в тысячу раз выше и составлять 10 миллионов градусов. Когда в 1920 году британский физик сэр Артур Эддингтон впервые выдвинул предположение, что такое слияние может являться источником энергии Солнца, ему сразу же указали на наличие потенциальной проблемы в его теории. Тем не менее Эддингтон был твердо убежден, что превращение водорода в гелий посредством ядерного синтеза и есть источник энергии Солнца, а также что решение загадки с низкой температурой скоро будет найдено. «Гелий, с которым мы имеем дело, должен образоваться в какое-то время в каком-то месте, — сказал он. — Мы не спорим с критиком, утверждающим, что звезды недостаточно горячие для этого процесса, а предлагаем ему поискать более горячее место».
Превращение протонов в нейтроны — настолько неэффективный процесс, что в расчете на килограмм массы Солнце в несколько тысяч раз менее результативно превращает массу в энергию, чем организм человека. Один килограмм вещества Солнца генерирует в среднем всего 1/5000 ватт энергии, тогда как человеческий организм — как правило, немногим более одного ватта на килограмм веса. Безусловно, Солнце очень большое, что с лихвой компенсирует его относительную неэффективность.
В этой книге мы постоянно подчеркиваем тот факт, что Вселенная живет по определенным законам. Следовательно, не стоит приходить в слишком большой восторг по поводу уравнения, которое (как в случае уравнения E = mc2) говорит нам, что могло бы произойти. Существует огромная разница между нашим воображением и реальным ходом событий. И хотя возможности, которые открывает уравнение E = mc2, приводят нас в сильное возбуждение, мы все же должны понимать, как именно законы физики делают возможным процесс разрушения массы и выделения энергии. Безусловно, из этого уравнения не вытекает логический вывод о том, что мы имеем право превращать массу в энергию по своему усмотрению.
Одним из самых замечательных достижений в физике за прошедшие сто лет стало осознание того, что, по всей вероятности, нам необходимо совсем немного законов для объяснения почти всех физических процессов, во всяком случае теоретически. Казалось, Ньютон достиг этой цели, когда еще в конце XVII века сформулировал законы динамики. На протяжении следующих двух сотен лет почти не было научных доказательств обратного. Однако сам Ньютон более скромно оценивал ситуацию. Однажды он сказал: «Я был подобен мальчику, который играет на морском берегу и время от времени развлекается тем, что ищет более гладкий камешек или более красивую ракушку, тогда как великий океан истины оставался для меня неизведанным». Эти слова прекрасно передают суть скромного чуда, которое может совершить время, потраченное на изучение физики. Когда видишь всю красоту природы, кажется ненужным и даже глупым претендовать на открытие абсолютной теории. Однако вопреки этой весьма уместной философской скромности в плане оценки научной деятельности постньютоновская картина мира гласила, что все сущее может состоять из крохотных элементов, которые послушно подчиняются законам физики, сформулированным Ньютоном. Следует признать, что при этом оставались на первый взгляд несущественные вопросы, не получившие ответа: как все сущее на самом деле держится вместе? Из чего в действительности состоят эти крохотные элементы? Однако мало кто сомневался, что в основе всего лежит теория Ньютона. Предполагалось, что остальное сведется к выяснению деталей. Однако в XIX столетии ученые наблюдали все больше явлений, которые не подчинялись законам Ньютона и со временем создали предпосылки для теории относительности Эйнштейна и квантовой теории. Как и следовало ожидать, законы Ньютона были опровергнуты, или, если точнее, было показано, что они представляют собой приближение более точной картины мира. Сто лет спустя мы, похоже, снова игнорируем уроки прошлого и заявляем, что у нас (почти) есть теория, объясняющая все, что происходит во Вселенной. Вполне возможно, что мы опять ошибаемся, и это не так уж плохо. Следует помнить, что в прошлом можно найти много доказательств несостоятельности научного высокомерия. Кроме того, представление о том, что мы знаем об устройстве мира достаточно или даже все, что нужно, всегда приносило и, по всей видимости, будет приносить огромный вред человеческому духу. В 1810 году Гемфри Дэви сказал в своей публичной лекции такие замечательные слова: «Ничто не сказывается на развитии человеческого разума настолько пагубно, как предположение, что наши научные взгляды неоспоримы, что в природе больше нет новых загадок, что наши победы завершились и что больше нет новых миров, которые можно было бы покорять».
Не исключено, что вся физика в известном нам виде — это всего лишь вершина айсберга, а может, мы действительно приближаемся к открытию «теории всего». Как бы то ни было, одно можно сказать наверняка: в текущий момент у нас есть наглядно доказанная теория, ставшая результатом кропотливого труда тысяч ученых во всем мире, которую мы можем использовать для объяснения широкого диапазона явлений. Она удивительная, ибо многое в себе объединяет, хотя ее основное уравнение может поместиться на обратной стороне конверта.
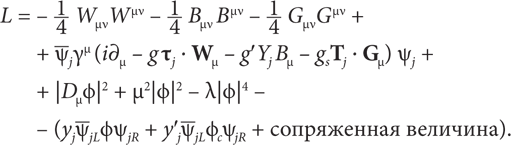
Мы называем это важнейшее уравнение центральным, и оно лежит в основе того, что сейчас известно как стандартная модель физики элементарных частиц. Это уравнение вряд ли будет что-то значить для большинства читателей, но мы не можем не привести его здесь.
Безусловно, только профессиональные физики поймут все детали данного уравнения, но мы разместили его не для них. Прежде всего мы хотели показать читателям одно из самых замечательных уравнений в физике — немного ниже мы объясним, почему оно такое замечательное. Помимо этого, существует реальная возможность прочувствовать всю красоту процессов, описываемых этим уравнением, просто поговорив о приведенных в нем символах даже без каких-либо знаний математики. Давайте для начала проанализируем область действия основного уравнения: какова его задача? Какую миссию оно выполняет? Задача этого уравнения — описать правила, по которым каждая частица во Вселенной взаимодействует с остальными частицами. Единственное исключение состоит в том, что, ко всеобщему огорчению, в этом уравнении не учитывается гравитация. Но несмотря на ее отсутствие, его область действия все же настолько перспективна, что это вызывает восхищение. Построение центрального уравнения — вне всяких сомнений, одно из величайших достижений в истории физики.
Позвольте уточнить, что мы подразумеваем под взаимодействием двух частиц. Мы имеем в виду, что взаимодействие частиц друг с другом оказывает определенное влияние на их движение. Например, две частицы могут разлететься в разные стороны, изменив при этом направление движения. Или могут вращаться друг вокруг друга по орбите, попав в ситуацию, которую физики называют состоянием связи. Атом — один из примеров такого состояния. В случае атома водорода один электрон и один протон связаны друг с другом в соответствии с правилами, сформулированными в основном уравнении. В предыдущей главе мы с вами много говорили об энергии связи, а также о правилах ее расчета для атома, молекулы или атомного ядра, которые отображены в центральном уравнении. В определенном смысле знание правил игры означает, что мы описываем устройство Вселенной на самом фундаментальном уровне. Так каковы же частицы, из которых все состоит, и как они взаимодействуют друг с другом?
В стандартной модели в качестве отправной точки используется факт существования материи. Точнее говоря, эта модель предполагает существование шести типов кварков, трех типов заряженных лептонов (один из которых электрон) и трех типов нейтрино. Вы можете увидеть, как эти частицы вещества появляются в основном уравнении: они обозначены символом Ψ (произносится как «пси»). Кроме того, у каждой частицы есть соответствующая античастица. Антиматерия — это не продукт научной фантастики, а неотъемлемая составляющая Вселенной. В 20-х годах ХХ века британский физик-теоретик Поль Дирак первым осознал необходимость в антиматерии, когда предсказал существование партнера электрона под названием позитрон, который должен был иметь точно такую же массу, но противоположный электрический заряд. Мы уже встречались с позитронами и знаем их как побочный продукт процесса слияния двух протонов и образования дейтрона. Одна из самых впечатляющих характеристик успешной научной теории состоит в ее способности прогнозировать нечто такое, что прежде было неизвестно. Последующее наблюдение этого «нечто» в ходе эксперимента убедительно подтверждает тот факт, что мы поняли что-то истинное об устройстве Вселенной. Если углубиться в суть вопроса, можно констатировать следующее: чем больше прогнозов способна сделать теория, тем большее впечатление производит ее подтверждение в ходе экспериментов. Напротив, если эксперименты не позволяют обнаружить прогнозируемое явление, то теория не может быть верной и ее необходимо отбросить. В таком интеллектуальном поиске нет места для споров: эксперимент — это последний судья. Звездный час Дирака наступил через несколько лет после того, как Карл Андерсон осуществил первое непосредственное наблюдение позитронов, применив для этого космические лучи. За свой труд Дирак получил Нобелевскую премию в 1933 году, а Андерсон — в 1936-м. Каким бы загадочным ни казался позитрон, в наше время факт его существования подтверждается тем, что он используется в повседневной практике в больницах по всему миру. Использование позитронов в ПЭТ-сканерах (PET, positron emission tomography — позитронно-эмиссионная томография) позволяет врачам составить трехмерную карту организма. Скорее всего, Дирак не думал о диагностической визуализации, когда работал над идеей антиматерии. Это в очередной раз говорит о том, что понимание внутреннего устройства Вселенной приносит людям конкретную пользу.
Предположительно существует еще одна частица, но пока заявлять об этом с абсолютной уверенностью не стоит. Эта частица обозначается греческой буквой ϕ (произносится как «фи») и появляется в третьей и четвертой строках центрального уравнения. За исключением этой «еще одной» частицы все кварки, заряженные лептоны и нейтрино (а также их частицы-партнеры из антиматерии) были обнаружены в ходе экспериментов. Безусловно, их нельзя увидеть человеческим глазом. В последнее время это делается с помощью детекторов частиц, напоминающих фотокамеры с высоким разрешением, которые могут сделать мгновенный снимок элементарной частицы в момент ее мимолетного появления. Во многих случаях открыватели элементарных частиц получали Нобелевскую премию. Последней в 2000 году была обнаружена частица под названием тау-нейтрино. Этот призрачный кузен электронных нейтрино, излучаемых Солнцем в процессе ядерного синтеза, замыкает группу из 12 известных частиц материи.
Самые легкие кварки называются верхними и нижними. Из них построены протоны и нейтроны. В состав протонов входят главным образом два верхних и один нижний кварк, тогда как нейтроны состоят из двух нижних кварков и одного верхнего. Обычная материя образована из атомов, а в состав атомов входит ядро, сформированное из протонов и нейтронов, вокруг которых на достаточно большом расстоянии вращаются электроны. Таким образом, наряду с электронами верхние и нижние кварки — самые распространенные частицы в обычной материи. Кстати, их название не имеет специального значения. Американский физик Марри Гелл-Манн позаимствовал слово «кварк» из романа ирландского писателя Джеймса Джойса Finnegan’s Wake («Поминки по Финнегану»). Для того чтобы объяснить известные на то время частицы, Гелл-Манну необходимо было три кварка, а небольшой отрывок из романа Джойса казался для этого весьма подходящим:
Three quarks for Muster Mark!
Sure he has not got much of a bark
And sure any he has it’s all beside the mark.
Гелл-Манн впоследствии писал, что сначала намеревался произносить это слово как «кворк» — именно так оно звучало в его голове до того, как он нашел цитату из «Поминок по Финнегану». Поскольку слово quark в этом стихотворении рифмуется со словами Mark и bark, это создавало определенные проблемы. В итоге Гелл-Манн решил заявить, что это слово может означать quart — «кварта», то есть единица объема жидкости, а не более привычное «крик чайки». Это позволило ему сохранить первоначальное произношение термина. По всей вероятности, мы так и не узнаем, как правильно произносить это слово. Открытие еще трех кварков, последним из которых в 1995 году стал так называемый истинный кварк, дало повод считать происхождение этого термина еще более неподходящим. Пожалуй, это должно послужить уроком будущим физикам, которые попытаются найти в литературе расплывчатые обозначения для своих открытий.
Несмотря на все злоключения с присвоением имени новой частице, Гелл-Манн оказался прав в своем предположении, что протоны и нейтроны состоят из более мелких объектов. Эта гипотеза получила подтверждение, когда кварки в конце концов были обнаружены с помощью ускорителя элементарных частиц в Стэнфорде в 1968 году, через четыре года после формулировки первоначального теоретического прогноза. Марри Гелл-Манн и авторы эксперимента, получившие доказательства существования кварков, были впоследствии удостоены Нобелевской премии за свою работу.
Помимо частиц материи, о которых мы только что говорили, а также таинственной частицы ϕ есть и несколько других частиц, о которых необходимо упомянуть, это W и Z, а также фотон и глюон. Для начала следует сказать пару слов о роли этих частиц. Они отвечают за взаимодействие между всеми остальными частицами. Если бы их не было, ничто во всей Вселенной не поддерживало бы ни с чем взаимодействия. Будем говорить, что их задача — переносить силу взаимодействия между частицами материи. Фотон — частица, которая отвечает за перенос этой силы между электрически заряженными частицами, такими как электроны и кварки. Фотон в прямом смысле слова лежит в основе всех физических законов, открытых Фарадеем и Максвеллом, а в качестве бонуса образует видимый свет, радиоволны, инфракрасное и микроволновое излучение, рентгеновские лучи и гамма-излучение. Представление о том, как поток фотонов, излучаемых электрической лампочкой, отскакивает от страницы этой книги и попадает в ваши глаза, которые являются не чем иным, как сложным детектором фотонов, совершенно правильное. Физик сказал бы, что фотон выступает в качестве инструмента электромагнитного взаимодействия. Глюон встречается в повседневной жизни не так часто, как вездесущий фотон, но его роль не менее важна. В центре каждого атома находится ядро. Атомное ядро — это шар, имеющий положительный электрический заряд (вспомните, что протоны — это электрически заряженные частицы, тогда как нейтроны — нет). Подобно тому что происходит, когда вы пытаетесь приблизить друг к другу одноименные полюсы магнита, все протоны отталкиваются друг от друга под влиянием электромагнитного взаимодействия. Они просто не желают соединяться друг с другом и предпочли бы разлететься в разные стороны. К счастью, это не случается, благодаря чему и существуют атомы. Глюон выступает в качестве связующего звена, которое «склеивает» протоны в атомном ядре друг с другом (клей на английском — glue, отсюда и название глюона). Кроме того, глюон отвечает за поддержание взаимодействия между кварками в составе протонов и нейтронов. Оно должно быть достаточно мощным, чтобы преодолеть электромагнитную силу отталкивания между протонами, поэтому его и называют сильным взаимодействием.
В данном контексте частицы W и Z можно объединить в одну группу. Частица W отвечает за взаимодействие, которое превращает протон в нейтрон в процессе образования дейтрона в сердце звезды. Превращение протонов в нейтроны (и наоборот) — не единственное, за что отвечает это слабое взаимодействие. Оно отвечает за сотни разных взаимодействий между существующими в природе элементарными частицами, многие из которых были изучены в ходе таких экспериментов, которые проводятся в CERN. Если не считать того, что благодаря частицам W и Z светит Солнце, они напоминают глюон — тем, что не так часто наблюдаются в повседневной жизни. Нейтрино поддерживают взаимодействие только посредством частиц W и Z, именно поэтому они столь неуловимы. Как мы видели в предыдущей главе, поток из многих миллиардов нейтрино каждую секунду пронизывает вашу голову, но вы при этом ничего не чувствуете, поскольку взаимодействие, которое переносят частицы W и Z, очень слабое. Наверное вы уже догадались, что мы назвали его слабым взаимодействием.
До настоящего момента мы всего лишь быстро прошлись по списку частиц, которые «обитают» в основном уравнении. Эти 12 частиц материи должны быть априори включены в теорию, хотя на самом деле мы даже не знаем, почему их именно столько. Благодаря наблюдениям процесса распада частиц Z на нейтрино, которые проводились в 1990-х годах в CERN, у нас действительно есть доказательства того, что таких частиц 12. С другой стороны, для создания Вселенной, по всей видимости, достаточно всего четырех частиц (таких как верхний и нижний кварки, электрон и электронное нейтрино), поэтому существование остальных восьми частиц остается загадкой. Мы считаем, что они сыграли важную роль на раннем этапе формирования Вселенной, но как именно они проявляли или проявляют свое действие в современной жизни — один из главных вопросов физики, ответ на который пока не найден.
Что касается стандартной модели, то все упомянутые в ее центральном уравнении двенадцать частиц — это элементарные частицы, которые не могут быть разделены на более мелкие части и представляют собой неделимые структурные элементы. Пожалуй, это действительно противоречит здравому смыслу: на первый взгляд было бы вполне естественным предположить, что любую маленькую частицу можно (теоретически) разделить пополам. Однако квантовая теория работает совсем не так, а наш здравый смысл и в этот раз нельзя назвать хорошим ориентиром в области фундаментальной физики. Согласно стандартной модели эти частицы не имеют субструктуры. Их называют «точечными» и считают конечным элементом материи. В свое время вполне может оказаться, что в ходе какого-либо эксперимента будет обнаружена возможность расщепления кварка на более мелкие фрагменты. Однако все дело в том, что так быть не должно: точечные частицы действительно могут оказаться неделимыми, и тогда вопросы об их субструктуре станут бессмысленными. Таким образом, мы имеем группу частиц, из которых построен наш мир, а также основное уравнение — ключ к пониманию того, как эти частицы взаимодействуют друг с другом.
Однако мы не упомянули об одном тонком моменте: хотя мы постоянно говорим о частицах, на самом деле это не совсем корректный термин. Это не частицы в общепринятом значении этого слова. Они не перемещаются в пространстве, отскакивая друг от друга, подобно миниатюрным бильярдным шарам. Вместо этого они взаимодействуют друг с другом наподобие того, как взаимодействуют волны на поверхности воды, создавая тени на дне бассейна. Эти частицы имеют волновые характеристики, оставаясь при этом частицами. Такая картина весьма парадоксальна и вытекает из квантовой теории. Точная природа волновых взаимодействий строго (то есть математически) задается основным уравнением. Но откуда мы знали, что именно необходимо включить в это уравнение, когда писали его? По каким принципам оно построено? Прежде чем заняться этими важными вопросами, давайте глубже проанализируем основное уравнение и попытаемся понять, что именно оно означает.
Первая строка уравнения описывает кинетическую энергию, которая переносится частицами W и Z, фотоном и глюоном, и говорит нам о том, как они взаимодействуют друг с другом. Мы еще не обсуждали эту возможность, но она существует: глюоны могут вступать во взаимодействие с другими глюонами, а частицы W и Z могут взаимодействовать между собой. Частица W может также взаимодействовать с фотоном. В этом перечне отсутствует возможность взаимодействия фотонов с фотонами, поскольку оно не происходит. И это большая удача, иначе нам было бы трудно что-либо увидеть. То, что вы можете читать эту книгу, — в каком-то смысле удивительный факт. Дело в том, что свет, исходящий от этой страницы, не отклоняется от пути к вашим глазам под воздействием пересекающего этот путь света от других окружающих вас объектов, которые вы могли бы увидеть, повернув голову. Фотоны буквально проскакивают мимо, не обращая внимания друг на друга.
Большая часть действия происходит во второй строке основного уравнения. Эта строка демонстрирует, как каждая частица материи во Вселенной взаимодействует с остальными частицами. В ней отображены взаимодействия, посредниками в которых выступают фотоны, частицы W и Z, а также глюоны. Кроме того, во второй строке отображена кинетическая энергия всех частиц материи. Третью и четвертую строки уравнения мы не будем пока рассматривать.
Как мы уже подчеркивали, за исключением гравитации в основном уравнении отображены все известные нам фундаментальные законы физики. Это уравнение включает в себя закон электростатического отталкивания в том виде, в котором его описал в количественной форме Шарль Огюстен де Кулон в конце XVIII столетия, а также все аспекты электричества и магнетизма, если уж на то пошло. Понятия, введенные Фарадеем, и прекрасные уравнения Максвелла становятся очевидными, если мы «спросим» основное уравнение, как частицы с электрическим зарядом взаимодействуют друг с другом. И конечно же, вся эта формула твердо опирается на специальную теорию относительности Эйнштейна. В действительности та часть стандартной модели, которая объясняет, как взаимодействуют свет и материя, называется квантовой электродинамикой. Слово «квантовая» напоминает нам, что квантовая теория внесла некоторые, в большинстве случаев совсем незначительные, изменения в уравнения Максвелла, повлекшие за собой едва заметные последствия, которые впервые изучал в середине ХХ века Ричард Фейнман и другие ученые. Как мы уже видели, основное уравнение содержит также физические основы сильных и слабых взаимодействий. Свойства этих трех сил природы описаны в уравнении во всех деталях, а это означает, что правила игры сформулированы с математической точностью, без какой бы то ни было неопределенности и избыточности. Таким образом, если оставить в стороне гравитацию, мы имеем некий приближенный вариант теории великого объединения. Справедливо также то, что ни в ходе экспериментов, ни в процессе наблюдения космического пространства никто так и не нашел никаких доказательств того, что во Вселенной действует некая пятая сила. Большинство повседневных явлений можно полностью объяснить с помощью законов электромагнетизма и гравитации. Слабое взаимодействие поддерживает горение Солнца, но в повседневной жизни на Земле оно почти не ощущается. С другой стороны, сильное взаимодействие сохраняет целостность атомных ядер, но редко распространяется за пределы ядра, а значит, эта огромная сила не проявляет своего действия в нашем макроскопическом мире. Иллюзию того, что такие твердые вещи, как столы и стулья, на самом деле твердые, поддерживает электромагнитное взаимодействие. На самом деле материя — это главным образом пустое пространство. Представьте себе, что вы увеличили атом настолько, что его ядро стало размером с горошину. В таком случае электроны были бы песчинками, с высокой скоростью вращающимися вокруг ядра на расстоянии в один километр, а все остальное — пустота. Аналогия с песчинкой — в какой-то мере преувеличение, так как мы не должны забывать, что элементарные частицы действуют скорее как волны, а не как песчинки. Но этой аналогией мы хотели показать относительный размер атома в сравнении с размером ядра, расположенного в его центре. Твердость возникает, когда мы пытаемся протолкнуть облако вращающихся вокруг ядра электронов через облако электронов соседнего атома. Поскольку электроны имеют электрический заряд, эти облака отталкиваются и не дают атомам пройти сквозь друг друга, хотя они и представляют собой в основном пустое пространство. Мысль о пустоте материи возникает, когда мы смотрим через окно. Хотя оконное стекло кажется твердым, свет без труда проходит сквозь него, позволяя нам увидеть окружающий мир. В каком-то смысле удивительно другое: почему непрозрачен брусок дерева!
Безусловно, тот факт, что можно описать так много физических законов одним уравнением, производит впечатление. Это красноречивее всяких слов говорит в пользу утверждения Юджина Вигнера о «непостижимой эффективности математики». Почему бы этому миру не быть гораздо сложнее? Разве есть у нас право втискивать так много физических явлений в одно уравнение? Разве мы не должны вносить все эти явления и факты в огромные базы данных и энциклопедии? На самом деле никто не знает, почему природа позволяет описывать себя в столь краткой форме, но верно и то, что такая бесспорная исходная элегантность и простота и есть одна из причин, почему многие физики занимаются своим делом. Напоминая себе о том, что природа может и не подчиняться столь чудесному упрощению, мы можем хотя бы какое-то время восхищаться той глубинной красотой, которую открыли.
Хотя уже было сказано многое, это еще не все. Мы еще не упомянули о предмете особой гордости стандартной модели: она не только охватывает электромагнитное, сильное и слабое взаимодействие, но еще и объединяет два из них. На первый взгляд может показаться, что явления электромагнитного и слабого взаимодействия никак друг с другом не связаны. Электромагнетизм — исконное явление реального мира, которое все мы понимаем на интуитивном уровне, тогда как слабое взаимодействие скрыто в загадочном субъядерном мире. Как это ни удивительно, стандартная модель говорит о том, что эти две силы — фактически проявление одного и того же. Посмотрите еще раз на вторую строку основного уравнения. Даже не зная математики, вы сможете увидеть взаимодействие между частицами вещества. Те фрагменты второй строки, в которых присутствуют символы W, B и G (для глюона), расположены между двумя частицами вещества, Ψ, а это значит, что они говорят нам, как частицы вещества «объединяются» с переносчиками взаимодействия, но с одним важным уточнением. Фотон частично скрыт под символом W и частично — под символом B, но ведь здесь же обитает и Z! Частица W полностью скрыта в символе W. Создается впечатление, что это математическое соотношение рассматривает в качестве фундаментальных объектов W и B, но их сочетание как по волшебству образует фотон и частицу Z. В итоге электромагнитное взаимодействие (которое переносит фотон) и слабое взаимодействие (которое переносят частицы W и Z) связаны друг с другом. Это означает, что свойства, которые можно измерить в ходе экспериментов с электромагнитными явлениями, должны быть связаны со свойствами, измеряемыми в ходе экспериментов со слабым взаимодействием. Это весьма впечатляющий прогноз стандартной модели. И он получил подтверждение: создатели стандартной модели Шелдон Глэшоу, Стивен Вайнберг и Абдус Салам были награждены Нобелевской премией, поскольку их теория помогла предсказать массу частиц W и Z задолго до того, как в 1980-х годах эти частицы были открыты в CERN. Все члены уравнения прекрасно согласуются друг с другом. Но откуда Глэшоу, Вайнберг и Салам знали, что именно следует в нем записать? Как они поняли, что сочетание W и B образует фотон и частицу Z? Ответить на этот вопрос — значит на мгновение увидеть прекрасную сущность современной физики элементарных частиц. Глэшоу, Вайнберг и Салам не просто догадались обо всем, у них в руках была важная путеводная нить: этот мир симметричен.
Симметрия проявляется повсюду. Поймайте снежинку и внимательно присмотритесь к этому самому прекрасному из творений природы. Схема ее рисунка повторяется с математической точностью, как отражение в зеркале. Более обыденный пример — мяч, который выглядит одинаково, как бы вы его ни повернули. Если повернуть квадрат вокруг диагонали или оси, которая проходит через центры его противоположных сторон, на 180°, это не изменит его вид. В физике симметрия проявляется точно так же. Если мы сделаем что-то с уравнением, но оно не изменится, тогда то, что мы с ним сделали, будет называться симметрией уравнения. Это несколько абстрактное понятие, однако следует помнить, что уравнения — это инструмент, с помощью которого физики описывают взаимодействие реальных объектов. Простая, но значимая симметрия, присущая всем важным уравнениям в физике, — свидетельство того, что, если мы возьмем оборудование для проведения эксперимента и разместим его на поезде, эксперимент даст те же результаты (при условии, что поезд движется без ускорения). Мы уже знакомы с этой идеей: речь идет о принципе относительности Галилея, лежащем в основе теории Эйнштейна. Если говорить в терминах симметрии, уравнения, описывающие наш эксперимент, не зависят от того, где именно он проводится: на железнодорожной платформе или в поезде, поэтому сам факт перемещения оборудования для проведения эксперимента — симметрия данного уравнения. Мы уже знаем, что этот простой факт в конечном счете подтолкнул Эйнштейна к открытию теории относительности. Так часто бывает: простая симметрия может повлечь далеко идущие последствия.
Теперь мы готовы поговорить о симметрии, которую использовали Глэшоу, Вайнберг и Салам, когда открыли стандартную модель физики элементарных частиц. У нее довольно причудливое название: калибровочная симметрия. Почему именно калибровочная? Прежде чем объяснять, что это значит, позвольте рассказать о том, что это нам дает. Давайте представим, что мы — Глэшоу, Вайнберг и Салам, ломающие голову над поиском теории, описывающей взаимодействие одних вещей с другими. Начнем с решения построить теорию, касающуюся крохотных неделимых частиц. Эксперименты показали, какие из этих частиц действительно существуют, поэтому наша теория должна охватывать их все, в противном случае она будет поверхностной. Безусловно, мы могли бы поразмышлять еще немного и попытаться понять, почему именно эти частицы должны быть теми, из которых образовано все сущее во Вселенной, или почему они должны быть неделимыми, но это только отвлекло бы нас от главного. На самом деле это два очень важных вопроса, на которые до сих пор нет ответов. Одно из качеств хорошего ученого — его способность определить, какие вопросы задать, для того чтобы двигаться дальше, а какие лучше отложить на потом. Так что давайте примем эти частицы как данность и попытаемся понять, как они взаимодействуют друг с другом. Если бы они не вступали во взаимодействие, мир был бы скучным: все проникало бы сквозь все остальное, ничто не объединялось бы в группы и у нас так и не было бы ядер, атомов, животных или звезд. Однако физика зачастую сводится к совершению небольших шагов. Не так уж трудно построить теорию частиц в случае, когда они не взаимодействуют друг с другом, — для этого достаточно вычеркнуть из второй строки основного уравнения фрагменты с участием W, B и G. И получим квантовую теорию всего, но без каких-либо взаимодействий. Вот мы и предприняли наш первый маленький шаг. А теперь начинается волшебство. Мы выдвинем требование о том, что в нашем мире, а значит, и в нашем уравнении должна присутствовать калибровочная симметрия. Это повлечет за собой поразительные последствия: оставшаяся часть второй строки и вся первая строка уравнения возникнут «просто так». Другими словами, мы будем вынуждены внести изменения в версию уравнения без взаимодействий, если хотим удовлетворить требования калибровочной симметрии. Совершенно неожиданно мы перешли от самой скучной в мире теории к той, в которой существует фотон, частицы W и Z, а также глюон. Более того, они отвечают за перенос всех взаимодействий между частицами. Иными словами, мы получили теорию, способную описать структуру атомов, сияние звезд и даже совокупность таких сложных объектов, как человеческие существа, — и все это благодаря применению концепции симметрии. У нас теперь есть первые две строки теории почти всего, и остается только объяснить, что представляет собой эта удивительная симметрия, а затем рассказать о двух последних строках основного уравнения.
Симметрия снежинки носит геометрический характер, поэтому ее можно увидеть собственными глазами. Симметрия, лежащая в основе принципа относительности Галилея, — это не то, что можно увидеть глазами, но все же можно понять, даже если это абстракция. Калибровочная симметрия подобна принципу Галилея в том, что она носит абстрактный характер, хотя при наличии воображения уловить ее суть не так уж трудно. Для того чтобы помочь вам свести воедино приведенные здесь описания с основными математическими понятиями, мы анализировали центральное уравнение. Давайте сделаем это снова. Как мы уже говорили, частицы вещества представлены в нем греческим символом Ψ. Теперь копнем еще глубже. То, что обозначают символом Ψ, называется полем. Это может быть поле электрона, или поле верхнего кварка, или любой другой частицы, входящей в стандартную модель. В том месте, где поле самое сильное, вероятнее всего, и находится частица. Пока что нас интересуют электроны, но то же самое верно и для любых других частиц, от кварков до нейтрино. Если в каком-то месте поле имеет нулевое значение, частицы там не будет. Вы можете даже представить себе такое поле в виде реального поля с травой или, что еще лучше, в виде волнообразного ландшафта с холмами и впадинами. Там, где холмы, поле самое сильное, а где впадины — самое слабое. Мы предлагаем вам мысленно нарисовать себе поле электрона. Возможно, вас удивляет тот факт, что наше основное уравнение носит столь неопределенный характер. Оно не работает с достоверными событиями. Более того, мы даже не можем отслеживать движение электрона. Все, что мы можем, — это сказать, что вероятность его пребывания в одном месте (там, где расположена гора) выше, тогда как в другом (там, где впадина) — ниже. Мы можем присвоить определенные значения вероятности пребывания электрона в том или ином месте, но этим все и ограничивается. Такая расплывчатость описания мира на уровне очень малых расстояний объясняется тем, что здесь правит бал квантовая теория, имеющая дело только с вероятностью наступления тех или иных событий. Создается впечатление, что в основе таких концепций, как местоположение и импульс в масштабе малых расстояний, действительно лежит некая фундаментальная неопределенность. Кстати, Эйнштейну очень не нравилось то, что наш мир должен функционировать в соответствии с законами вероятности, и он даже высказал свою знаменитую мысль: «Бог не играет в кости». Тем не менее он был вынужден признать, что квантовая теория оказалась невероятно успешной. Она объясняет результаты всех экспериментов, проведенных в области субатомных частиц, и без нее мы не понимали бы, как работают микросхемы в современных компьютерах. Возможно, в будущем кто-то создаст еще более эффективную теорию, но пока что квантовая теория — наша лучшая попытка. На протяжении всего повествования мы изо всех сил старались обратить ваше внимание на следующий факт: нет абсолютно никаких оснований для того, чтобы окружающий мир подчинялся нашему здравому смыслу, когда мы пытаемся объяснить явления, выходящие за рамки повседневного опыта. Мы развивались в условиях механики большого мира, а не квантовой механики.
Но вернемся к нашей задаче. Поскольку квантовая теория определяет правила игры, мы просто обязаны поговорить о полях электронов. Однако недостаточно просто установить поле и определить ландшафт. В математике квантовых полей скрыта одна неожиданность, состоящая в наличии определенной избыточности. Математика гласит, что для любой точки ландшафта, будь то холм или впадина, мы должны указывать не только значение поля в определенной точке (скажем, высоту над уровнем моря в нашей аналогии с реальным полем), соответствующей вероятности пребывания в ней частицы, но еще и то, что обозначают термином «фаза поля». Такую фазу легче всего представить себе в виде циферблата (или круглой шкалы), только с одной стрелкой. Если стрелка указывает на 12 часов, это одна возможная фаза, а если на шесть — другая. Представьте себе, что мы разместили небольшие циферблаты во всех без исключения точках нашего ландшафта, причем каждый из них говорит нам о фазе, в которой находится поле в данной точке. Безусловно, это ненастоящие часы (и они, разумеется, не измеряют время). Существование фазы — это то, что было известно специалистам по квантовой физике задолго до Глэшоу, Вайнберга и Салама. Более того, все знали, что, хотя относительная фаза между различными точками поля имеет значение, фактические показатели не играют никакой роли. Например, вы могли бы перевести все свои крохотные часы на десять минут вперед — и ничего бы не изменилось. Главное здесь то, что вы должны перевести все часы на одинаковое количество минут. Если забудете перевести хотя бы одни из них, это будет означать, что вы описываете другое поле электронов. Следовательно, в математическом описании мира присутствует определенная избыточность.
В 1954 году, за несколько лет до того, как Глэшоу, Вайнберг и Салам создали стандартную модель, Чжэньнин Янг и Роберт Миллс из Брукхейвенской национальной лаборатории задались вопросом, какое значение может иметь избыточность, связанная с введением фазы. Физика часто получает дальнейшее развитие, когда ученые начинают обыгрывать те или иные идеи без достаточных на то оснований. Янг и Миллс именно этим и занимались. Им захотелось узнать, что произошло бы, если бы Вселенной не было никакого дела до фазы. Другими словами, они решили сыграть с математическими уравнениями, перемешав все фазы, и попытались понять, какими могут быть последствия. Это может показаться странным, но если вы посадите пару физиков в одном кабинете и дадите им свободу действий, то именно этим они и займутся. Возвращаясь к нашей аналогии с ландшафтом, вы можете себе представить, что идете по полю, безо всякой системы меняя показания маленьких циферблатов на разные величины. То, что произойдет, на первый взгляд выглядит достаточно просто: вам не позволено так поступать. Это не соответствует симметрии Вселенной.
Для того чтобы точнее сформулировать эту идею, давайте вернемся к основному уравнению и еще раз взглянем на его вторую строку. Теперь исключим из нее фрагменты, содержащие W, B и G. В итоге получим самую простейшую из возможных теорию частиц: частицы просто сидят без дела и никогда не вступают во взаимодействие друг с другом. Эта небольшая часть основного уравнения совершенно определенно не останется неизменной, если мы вдруг возьмем и перенастроим все маленькие часы (вряд ли вы сможете это увидеть, просто глядя на уравнение). Янг и Миллс знали это, но проявили большую настойчивость, поставив один очень важный вопрос: как можно изменить уравнение, чтобы оно все же осталось неизменным? Ответ поражает: необходимо вернуть те его фрагменты, которые мы только что исключили, — больше ничего для этого не подойдет. После этого частицы — переносчики взаимодействий как по волшебству появятся на свет и совершенно неожиданно мы перейдем от мира без взаимодействий к теории, которая способна описать наш реальный мир. Тот факт, что основному уравнению нет никакого дела до показателей на циферблатах (или калибров), — и есть то, что мы подразумеваем под калибровочной симметрией. Самое удивительное, что требование наличия калибровочной симметрии не оставляет нам выбора в том, что записывать в уравнении: калибровочная симметрия неизбежно приводит к основному уравнению. Другими словами, те силы, которые делают наш мир интересным, существуют как следствие того, что калибровочная симметрия — это и есть симметрия Вселенной. В качестве постскриптума добавим, что Янг и Миллс подали пример, но их работа главным образом представляла математический интерес и была выполнена задолго до того, как специалисты по физике элементарных частиц вообще узнали, какие частицы должна описывать фундаментальная теория. Именно Глэшоу, Вайнберг и Салам поняли, что идеи Янга и Миллса можно применить к описанию реального мира.
Итак, мы с вами увидели, как можно составить первые две строки основного уравнения, лежащего в основе стандартной модели физики элементарных частиц, и искренне надеемся, что нам удалось помочь вам получить представление о масштабе и содержании этого уравнения. Более того, мы убедились, что оно не носит произвольный характер — напротив, идея калибровочной симметрии неотвратимо приводит нас к нему. Теперь, когда мы лучше понимаем это самое важное из всех уравнений, можно вернуться к задаче, решить которую мы собирались с самого начала. Мы пытались понять, в какой степени законы природы действительно обеспечивают возможность превращения массы в энергию и наоборот. Разумеется, ответ содержится в основном уравнении, так как именно оно определяет правила игры. Но есть гораздо более привлекательный способ понять, что происходит и как частицы взаимодействуют друг с другом. Этот подход, активно использующий графическое представление, был введен в физику Ричардом Фейнманом.
Что произойдет, когда два электрона приблизятся друг к другу? Или два кварка? Или нейтрино и антимюон? И так далее. Все эти частицы вступят во взаимодействие в точном соответствии с правилами, заданными в основном уравнении. Два электрона в случае сближения оттолкнутся друг от друга, потому что имеют одинаковый электрический заряд, тогда как электрон и антиэлектрон будут притягиваться друг к другу, так как имеют противоположный электрический заряд. Все эти физические процессы описаны в первых двух строках основного уравнения и могут быть кратко обобщены в виде нескольких правил, которые можно представить в графическом виде. На самом деле не так уж трудно понять основные положения этого уравнения, хотя изучение деталей может потребовать более напряженных усилий. Мы с вами остановимся на ключевых положениях.
Давайте еще раз посмотрим на вторую строку основного уравнения. Член уравнения, который содержит два символа Ψ и один символ G, —единственная часть уравнения, описывающая сильное взаимодействие между двумя кварками. Поля двух кварков и глюон взаимодействуют в одной точке пространства-времени — именно об этом говорит нам основное уравнение. Более того, это единственный способ, посредством которого они могут вступить во взаимодействие. Данная часть уравнения показывает нам, как взаимодействуют кварки и глюоны, причем этот способ взаимодействия однозначно задается уравнением, если мы ставим перед собой цель построить теорию, основанную на калибровочной симметрии. У нас просто не остается выбора. Фейнман понял, что такая простота свойственна, по сути, всем базовым взаимодействиям, и начал рисовать диаграммы для каждого взаимодействия, которое допускает теория. На рис. 14 показано, как специалисты по физике элементарных частиц обычно изображают в графическом виде взаимодействие между кварком и глюоном. Волнистая линия представляет глюон, прямая — кварк или антикварк. На рис. 15 изображены другие разрешенные стандартной моделью взаимодействия, вытекающие из первых двух строк основного уравнения. Пусть вас не беспокоят детали этих диаграмм — главное, что мы можем их записать и что их не так уж много. Частицы света (фотоны) обозначены символом γ, а частицы W и Z — своими символами. Шести кваркам соответствует общее обозначение q, нейтрино присвоен символ ν (произносится как «ню»), а три электрически заряженных лептона (электрон, мюон и тау) представлены символом l. Античастицы отмечены горизонтальной линией над соответствующим символом. А вот самый изящный аспект такого представления. Эти графические изображения содержат то, что физики называют «вершины взаимодействия». Вы можете «сшивать» эти вершины в более крупные диаграммы. Любая диаграмма, которую можно построить таким образом, отображает процесс, который может происходить в природе. И наоборот, если у вас не получается построить диаграмму, стало быть, данный процесс невозможен.
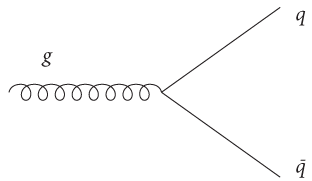
Рис. 14
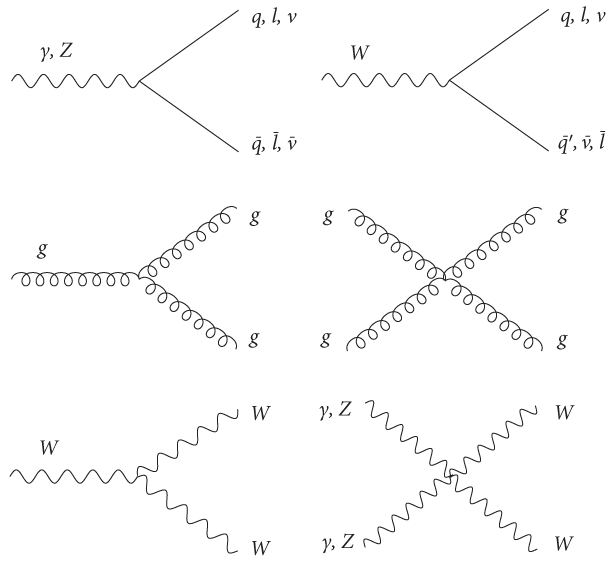
Рис. 15
Фейнман сделал нечто большее, чем просто ввел диаграммы. Он сопоставил с каждой вершиной математические правила, выведенные непосредственно из основного уравнения. Эти правила позволяют физикам строить сложные диаграммы и рассчитывать вероятность процесса, отображенного соответствующей диаграммой. Например, когда два электрона встречаются друг с другом, самая простая диаграмма, которая позволяет это отобразить, выглядит так, как показано на рис. 16, a. Мы говорим, что происходит рассеяние электронов посредством обмена фотонами. Эта диаграмма построена с помощью склейки двух вершин «электрон-фотон». Вы можете представить себе, как два электрона сближаются, двигаясь слева, разлетаются друг от друга в результате фотонного обмена и продолжают свой путь направо. На самом деле мы незаметно применили здесь еще одно правило: нам разрешается менять частицу на античастицу (и наоборот) при условии, что затем мы превратим ее в исходную частицу. На рис. 16, б показан еще один возможный способ сшивания вершин. Этот рисунок немного сложнее, но он также описывает вероятный способ взаимодействия между двумя электронами. После некоторых размышлений вы согласитесь, что существует бесконечное множество диаграмм и все они отображают возможные способы рассеяния электронов. К счастью для тех из нас, кому приходится выполнять расчеты, одни диаграммы более важны, чем другие. На самом деле сформулировать правило достаточно легко: в общем случае самые значимые — диаграммы с наименьшим количеством вершин. Следовательно, в случае пары электронов диаграмма на рис. 16, a наиболее важна, поскольку содержит всего две вершины. Это значит, что мы можем получить достаточно полное представление о происходящем, рассчитав только эту диаграмму с использованием правил Фейнмана. Замечательно то, что посредством математики можно получить описание физики взаимодействия двух электрических заряженных частиц друг с другом в том виде, в котором это взаимодействие открыли Фарадей и Максвелл. Но теперь мы можем заявить, что гораздо лучше понимаем происхождение этого физического процесса, так как установили его исходя из калибровочной симметрии. Кроме того, математические расчеты на основании правил Фейнмана дают нам нечто большее, чем просто еще один подход к пониманию физики XIX столетия. Даже в случае взаимодействия двух электронов мы можем вычислить небольшие поправки к предсказаниям Максвелла, которые позволят усовершенствовать его уравнения для их более точного соответствия экспериментальным данным. Следовательно, основное уравнение открывает новые горизонты. На самом деле мы только начинаем осваивать эту тему. Как мы уже говорили, стандартная модель описывает все, что нам известно о взаимодействии частиц друг с другом, и представляет собой исчерпывающую теорию сильного, слабого и электромагнитного взаимодействия, которой удалось даже объединить два из них. В эту амбициозную систему понимания того, как все взаимодействует во Вселенной, не включена только гравитация.
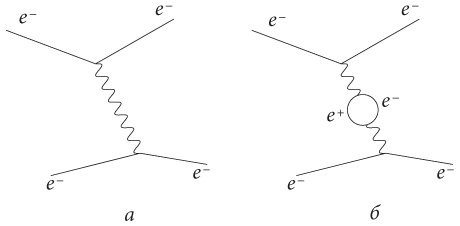
Рис. 16
Но давайте вернемся к нашей теме. Каким образом правила Фейнмана, позволяющие кратко сформулировать суть стандартной модели, задают способы, с помощью которых мы можем разрушать массу и превращать ее в энергию? Как мы можем применить эти правила для лучшего использования уравнения E = mc2? Для начала вспомним важный вывод, к которому мы пришли в главе 5: свет состоит из частиц без массы. Другими словами, фотоны — это частицы, не имеющие массы. В связи с этим мы можем нарисовать интересную диаграмму — как показано на рис. 17. Электрон и антиэлектрон (позитрон) сталкиваются друг с другом и аннигилируют, образуя при этом один фотон (давайте обозначим для ясности электрон символом e–, а позитрон — e+). Правила Фейнмана допускают такое взаимодействие. Эта диаграмма заслуживает особого внимания, поскольку отражает ситуацию, в которой мы начали с небольшого количества массы (электрон и позитрон имеют определенную массу), а закончили ее полным отсутствием (фотоном). Это первичный процесс разрушения материи, в ходе которого вся исходная энергия, заключенная в массе электрона и антиэлектрона, высвобождается в виде энергии фотона. Однако здесь есть одно противоречие. Аннигиляция в один фотон запрещена правилом, согласно которому все происходящее должно подчиняться законам сохранения энергии и импульса одновременно, а для данного процесса это невыполнимо (это не совсем очевидно, но мы не станем приводить здесь доказательства). Однако это противоречие легко обойти, просто образовав два фотона. На рис. 18 показана соответствующая диаграмма Фейнмана, где исходная масса снова полностью разрушилась и превратилась в энергию, в данном случае в два фотона. Процессы такого рода сыграли ключевую роль на раннем этапе формирования Вселенной, когда материя и антиматерия почти полностью уничтожили друг друга именно в ходе подобного взаимодействия. Сейчас мы наблюдаем остатки этого взаимного уничтожения. Астрономы установили, что на каждую частицу, существующую во Вселенной, приходится около 100 миллиардов фотонов. Другими словами, из каждых 100 миллиардов частиц материи, возникших после Большого взрыва, выжила только одна. Все остальные, как наглядно показывает диаграмма Фейнмана, использовали имеющуюся у них возможность избавиться от своей массы и превратиться в фотоны.
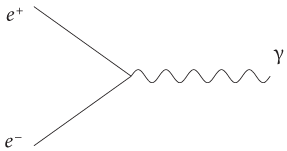
Рис. 17
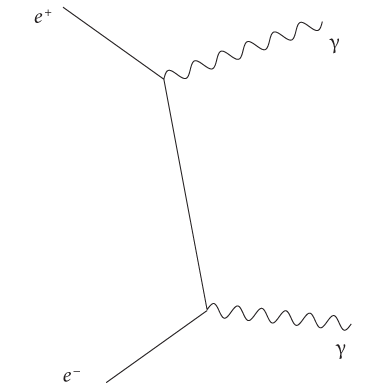
Рис. 18
На самом деле то вещество во Вселенной, из которого созданы звезды, планеты и люди, представляет собой крохотный остаток, сохранившийся после грандиозной аннигиляции массы, произошедшей в самом начале формирования Вселенной. Тот факт, что вообще что-то осталось, — не просто большая удача, а настоящее чудо! Мы до сих пор не совсем понимаем, почему это произошло. Вопрос, почему Вселенная не наполнена только светом и больше ничем, по-прежнему остается открытым, и во всем мире проводятся эксперименты, которые должны нам помочь найти на него ответ. В количестве умных идей нет недостатка, но нам еще предстоит найти убедительные экспериментальные данные или доказательства того, что все они ошибочны. Советский ученый Андрей Сахаров выполнил новаторскую работу в этой области. Он первым сформулировал критерии, которым должна удовлетворять любая успешная теория, преследующая цель ответить на вопрос, почему после Большого взрыва вообще осталась материя.
Мы с вами уже знаем, что у Вселенной есть механизм для разрушения массы, но, к сожалению, он не очень пригоден для использования на Земле, поскольку для этого необходим способ производства и хранения антиматерии. Нам негде добыть антиматерию, и, насколько нам известно, в открытом космосе ее тоже нет. В качестве топлива антиматерия представляется бесполезной, поскольку такого топлива просто нет. Антиматерию можно создать в лаборатории, но только потратив на это огромное количество энергии. Следовательно, хотя процесс аннигиляции материи и антиматерии представляет собой уникальный механизм превращения массы в энергию, он не поможет нам преодолеть мировой энергетический кризис.
А как насчет ядерного синтеза — процесса, который обеспечивает энергией Солнце? Как его можно описать в терминах стандартной модели? Для этого необходимо сфокусировать внимание на вершине диаграммы Фейнмана, в которой участвует частица W. На рис. 19 показано, что происходит, когда слияние двух протонов образует дейтрон. Если вы помните, протоны (в хорошем приближении) состоят из трех кварков: двух верхних и одного нижнего. Дейтрон состоит из одного протона и одного нейтрона, а нейтрон также содержит три кварка, но на этот раз речь идет об одном верхнем и двух нижних. Диаграмма показывает, как один из протонов можно превратить в нейтрон; как видите, ключевую роль в этом процессе играет частица W. Один из верхних кварков, входящих в состав протона, выделил частицу W и превратился в результате в нижний кварк, тем самым преобразовав протон в нейтрон. Согласно этой диаграмме частица W не остается в таком состоянии. Она прекращает свое существование и превращается в антиэлектрон и нейтрино. Частицы W, образующиеся в ходе формирования дейтрона, всегда погибают. На самом деле их никто никогда не видел, разве что в виде вещества, в которое они преобразуются, когда покидают этот мир. Как показывает опыт, почти все элементарные частицы умирают, потому что вершина диаграммы Фейнмана разрешает это. Исключение из этого правила наблюдается каждый раз, когда невозможно обеспечить сохранение энергии или импульса, а это чаще всего означает, что остаются только самые легкие частицы. Именно этим объясняется тот факт, что вещество, состоящее в основном из протонов, электронов и фотонов, доминирует в повседневной жизни. Этим частицам просто не на что распадаться: верхние и нижние кварки — самые легкие, электрон — самый легкий заряженный лептон, а фотон вообще не имеет массы. Например, мюон во многом идентичен электрону, за исключением того, что он тяжелее. Если вы помните, мы уже говорили об этом, когда обсуждали брукхейвенский эксперимент. Так как масса мюона изначально больше массы электрона, его превращение в электрон не нарушит закон сохранения энергии. Кроме того, как показано на рис. 20, правила Фейнмана разрешают такое превращение, а учитывая, что при этом выделяется также пара нейтрино, нет проблем и с сохранением импульса. Главное в том, что мюоны все же распадаются и живут в среднем 2,2 микросекунды. Кстати, 2,2 микросекунды — очень длительный период по шкале времени большинства интересных процессов в физике элементарных частиц. Напротив, электрон — самая легкая частица стандартной модели и ему просто не на что распадаться. Насколько можно судить, электрон, предоставленный самому себе, никогда не распадется, поэтому единственный способ победить его — заставить аннигилировать вместе с его партнером из антиматерии.
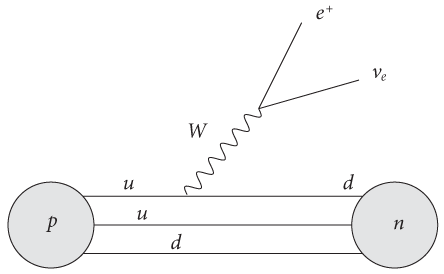
Рис. 19
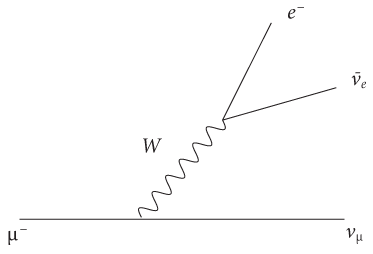
Рис. 20
Но вернемся к дейтрону. На рис. 19 показано, как он может образоваться в результате столкновения двух протонов. Кроме того, в каждом случае такого слияния можно обнаружить один антиэлектрон (позитрон) и одно нейтрино. Как мы уже отмечали, нейтрино поддерживают очень слабое взаимодействие со всеми остальными частицами Вселенной. Согласно основному уравнению именно так все и происходит, потому что нейтрино — единственная частица, которая вступает только в слабое взаимодействие. В итоге нейтрино, которые рождаются в сердце звезды, могут без всяких усилий сбежать от нее — они разлетаются во всех направлениях, а некоторые отправляются в сторону Земли. Подобно Солнцу, Земля для нейтрино почти прозрачна, и они проходят сквозь нее, даже не замечая, что она встретилась им на пути. Вместе с тем у каждого нейтрино все же есть небольшой шанс вступить во взаимодействие с атомом на Земле. Выше уже упоминалось, что это взаимодействие обнаруживается с помощью таких установок, как детектор Super-Kamiokande.
Как мы можем быть уверены в правильности стандартной модели, во всяком случае на том уровне точности, который обеспечивает современная экспериментальная база? На протяжении многих лет стандартную модель подвергали самым строгим тестам в разных лабораториях мира. Не стоит беспокоиться о том, что ученые предвзято относятся к этой теории. Те, кто проводит такие испытания, очень хотели бы найти слабые места или недостатки в стандартной модели и делают все возможное, чтобы ее развалить. Их мечта — хотя бы на мгновение увидеть новые физические процессы, которые могут открыть поражающие воображение новые перспективы и величественную картину внутреннего устройства Вселенной. Однако до настоящего времени стандартная модель выдержала все испытания.
Большой адронный коллайдер — самая последняя из крупных установок, используемых для проверки стандартной модели. Этот проект, в рамках которого сотрудничают ученые всего мира, преследует цель либо подтвердить, либо опровергнуть стандартную модель (немного ниже мы еще вернемся к БАК). Предшественником БАК был большой электрон-позитронный коллайдер (БЭПК), с помощью которого удалось провести ряд тонких тестов. Он находился внутри кольцевого тоннеля длиной 27 километров, вырытого под Женевой и несколькими живописными французскими деревнями. Этот коллайдер исследовал мир стандартной модели на протяжении 11 лет, с 1989 по 2000 год. Сильные электрические поля использовались для ускорения пучков электронов в одном направлении, а позитронов — в другом. Грубо говоря, ускорение заряженных частиц с помощью электрических полей напоминает механизм, применяемый в устаревших телевизионных приемниках с электронно-лучевыми трубками для выброса электронов на экран и создания изображения. Электроны выбрасываются с тыльной стороны устройства (поэтому старые телевизоры такие громоздкие), затем ускоряются электрическим полем и попадают на экран телевизора. Под воздействием магнита пучок электронов перемещается по экрану, создавая изображение.
В БЭПК также использовались магнитные поля, на этот раз для того, чтобы заставить частицы двигаться по кругу в соответствии с изгибом тоннеля. Весь смысл этой затеи состоял в том, чтобы устроить столкновение двух пучков частиц. Как мы уже знаем, столкновение электрона и позитрона может привести к аннигиляции обеих частиц, в результате которой их масса превратится в энергию. Именно эта энергия больше всего интересовала физиков, работавших с БЭПК, поскольку, согласно правилам Фейнмана, ее можно было бы превратить в более тяжелые частицы. На первом этапе работы ускорителя энергия электрона и позитрона очень близка к тому значению, которое существенно увеличивает вероятность создания частицы Z (вы можете просмотреть список правил Фейнмана в стандартной модели и убедиться, что аннигиляция электрон-позитронной пары, приводящая к рождению частицы Z, разрешена). На самом деле у частицы Z достаточно большая масса по сравнению с другими частицами: она почти в 100 раз тяжелее протона и примерно в 200 тысяч раз — электрона и позитрона. Следовательно, для того чтобы рождение частицы Z стало возможным, электрон и позитрон необходимо сталкивать друг с другом на скорости, очень близкой к скорости света. Безусловно, энергии, которая заключена в массе этих частиц и высвобождается после их аннигиляции, совершенно недостаточно для создания частицы Z.
Первоначальная цель, стоявшая перед БЭПК, была достаточно проста: вырабатывать частицы Z посредством многократного столкновения электронов и позитронов. При каждом столкновении пучков частиц существует довольно большая вероятность, что электрон из одного пучка аннигилирует с позитроном из другого пучка, что приведет к рождению одной частицы Z. Выстреливая эти пучки друг навстречу другу с большой скоростью, БЭПК за весь период существования смог образовать более 20 миллионов частиц Z в процессе аннигиляции электрон-позитронной пары.
Подобно другим частицам стандартной модели, частица Z нестабильна: она живет всего 10–25 секунды, прежде чем погибнуть. На рис. 21 показаны возможные варианты процесса создания частицы Z, которые представляли интерес для полутора тысяч физиков, работавших с БЭПК, не говоря уже о многих тысячах физиков по всему миру, с нетерпением ожидавших результатов. Благодаря использованию огромных детекторов частиц, окружающих точку столкновения и аннигиляции электрона и позитрона, специалисты по физике элементарных частиц смогли обнаружить и идентифицировать то, что образуется в процессе распада частицы Z. Современные детекторы, применяемые в физике элементарных частиц (такие как БЭПК), немного напоминают огромные многометровые цифровые фотоаппараты. Подобно самим ускорителям, эти детекторы представляют собой выдающееся достижение современного инженерного искусства. Расположенные в пещерах размером с собор, они могут с чрезвычайно высокой точностью измерить энергию и импульс единственной субатомной частицы. Эти установки — воплощение передовой инженерной мысли, что делает их прекрасным памятником нашего коллективного стремления к исследованию устройства Вселенной.
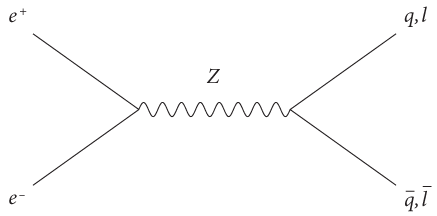
Рис. 21
Вооружившись этими детекторами и огромным парком высокопроизводительных компьютеров, ученые поставили перед собой одну из основных задач, решение которой подразумевало достаточно простую стратегию. Им необходимо было проанализировать полученные данные и идентифицировать столкновения, приводившие к рождению частицы Z, а затем определить характер ее распада для каждого такого столкновения. Иногда распад частицы Z приводил к образованию электрон-позитронной пары. А иногда — к созданию кварка и антикварка или, возможно, мюона и антимюона (см. рис. 21). Работа ученых сводилась к тому, чтобы подсчитать количество случаев распада частицы Z в соответствии с каждым из возможных сценариев, предусмотренных стандартной моделью, и сравнить полученные результаты с ожидаемыми показателями, предсказанными теорией. Имея в своем распоряжении данные о более чем 20 миллионах частиц Z, ученые смогли провести достаточно строгую проверку корректности стандартной модели. Как и следовало ожидать, ее результаты показали, что теория работает превосходно. Этот процесс, называемый измерением парциальной ширины, стал одним из самых важных испытаний стандартной модели, выполненных с помощью БЭПК. Впоследствии проводились еще многие испытания, и во всех случаях стандартная модель оказывалась верной. Когда в 2000 году БЭПК был закрыт, полученные с его помощью сверхточные данные позволили проверить стандартную модель с точностью 0,1 процента.
Прежде чем оставить тему тестирования стандартной модели, мы не можем не привести еще один пример эксперимента совершенно другого типа. Электроны (и многие другие элементарные частицы) ведут себя как крохотные магниты, и чтобы измерить этот магнитный эффект, были разработаны очень красивые эксперименты, не имеющие отношения к коллайдеру. Здесь нет никакого грубого столкновения материи и антиматерии. Вместо этого тщательно продуманные эксперименты позволяют ученым измерить магнетизм с поразительной точностью — до триллионной доли, аналогичной измерению расстояния от Лондона до Нью-Йорка с точностью до толщины человеческого волоса. Словно этого было недостаточно, физики-теоретики также работали не покладая рук. Они рассчитали тот же процесс. Раньше для выполнения вычислений такого рода достаточно было ручки и бумаги, но в наше время даже теоретикам не обойтись без хороших компьютеров.
Тем не менее, имея в своем распоряжении стандартную модель и трезвый ум, физики-теоретики рассчитали прогнозы этой модели, и полученные ими результаты полностью совпали с экспериментальными данными. До настоящего времени теория и эксперимент согласуются с точностью до десяти миллиардных долей. Это одно из самых точных испытаний любой теории, которая когда-либо создавалась во всех областях науки. К настоящему моменту, в немалой степени благодаря БЭПК и экспериментам с магнетизмом электронов, мы обрели большую уверенность в том, что стандартная модель физики элементарных частиц находится на правильном пути. Наша теория пребывает в прекрасном состоянии — за исключением одной последней детали, которая на самом деле достаточно серьезна. Что представляют собой две последние строки основного уравнения?
Мы признаем свою вину: мы скрывали информацию, имеющую бесспорно важное значение для тех поисков, которые мы предпринимаем в этой книге. Теперь пришло время раскрыть секрет. Требование наличия калибровочной симметрии, казалось бы, подразумевает, что все частицы стандартной модели не должны иметь массы. Это большое заблуждение. Любые объекты имеют массу, и чтобы это доказать, не нужны сложные научные эксперименты. Мы размышляли об этом на протяжении всей книги и вывели в итоге самое знаменитое уравнение в физике — E = mc2, в котором явно присутствует символ m. Эту проблему решают две последние строки основного уравнения. Когда мы поймем их суть, наше путешествие завершится, поскольку мы получим объяснение самого происхождения массы.
Проблему массы сформулировать очень легко. Если мы попытаемся включить ее непосредственно в основное уравнение, то неизбежно нарушим калибровочную симметрию, а она лежит в основе этой теории. Использование данной концепции позволило нам как по волшебству объяснить существование всех сил природы. Более того, в 1970-х годах физики-теоретики доказали, что отказ от калибровочной симметрии — не выход, поскольку в таком случае теория развалится на части и потеряет смысл. Выход из этой на первый взгляд тупиковой ситуации в 1964 году нашли три группы ученых, работавшие независимо друг от друга. Ученые Франсуа Энглер и Роберт Браут из Бельгии, Джеральд Гуральник, Карл Хаген и Том Киббл из Лондона, а также Питер Хиггс из Эдинбурга написали выдающиеся работы, которые привели к открытию того, что впоследствии получило известность как механизм Хиггса.
Как же объяснить, что такое масса? Предположим, вы начали с теории об устройстве Вселенной, в которой массы просто нет, и вы даже не изобрели бы термина для ее обозначения. Как мы уже знаем, в таком случае все частицы просто перемещались бы со скоростью света. А теперь представьте, что в рамках этой теории происходит нечто — скажем, некое событие, после которого различные частицы начинают двигаться с другой, более низкой скоростью и, разумеется, больше не перемещаются со скоростью света. В таком случае вы имели бы полное право заявить, что произошедшее отвечает за происхождение массы. Это «нечто» — механизм Хиггса, и нам пора объяснить, что это такое.
Представьте, что у вас завязаны глаза и вы держите на нитке шарик для пинг-понга. Дернув за нитку, вы придете к выводу, что на ее конце находится нечто имеющее совсем небольшую массу. Предположим, что шарик для пинг-понга не болтается свободно на нитке, а погружен в густой кленовый сироп. Дернув за нитку в этот раз, вы почувствуете значительное сопротивление и решите, что на конце нитки находится нечто гораздо тяжелее шарика для пинг-понга. А теперь представьте, что некий космический кленовый сироп пронизывает все пространство, причем он настолько вездесущ, своего рода фон для всего происходящего, что мы даже не замечаем его присутствия.
Безусловно, на этом аналогия с сиропом исчерпывается. Во-первых, это должен быть избирательный сироп, который удерживает кварки и лептоны, но беспрепятственно пропускает фотоны. Вы можете подумать, что можно было бы развить эту аналогию дальше, чтобы объяснить и этот феномен, но мы считаем, что донесли до вас основную мысль. Кроме того, мы не должны забывать, что это всего лишь аналогия. Разумеется, в работах Хиггса и его коллег никакой сироп не упоминается.
В действительности в этих работах идет речь о том, что мы называем сейчас полем Хиггса. Подобно полю электрона, с полем Хиггса связана частица — частица Хиггса. Так же как и в случае поля электрона, значения поля Хиггса изменчивы. Там, где это поле самое сильное, вероятность обнаружить частицу Хиггса наиболее высокая. Однако есть одно существенное отличие: поле Хиггса не является нулевым даже при отсутствии частиц Хиггса — именно в этом смысле оно напоминает вездесущий сироп. Все частицы в стандартной модели двигаются на фоне поля Хиггса, и некоторые из них попадают под его воздействие в большей степени, чем другие. Последние две строки основного уравнения охватывают именно этот физический процесс. Поле Хиггса представлено в уравнении символом ϕ, и фрагмент третьей строки, содержащий два символа ϕ вместе с B или W (которые в нашей сокращенной записи скрыты в символе D в третьей строке основного уравнения), — именно те члены уравнения, которые генерируют массу для частиц W и Z. Эта теория весьма разумно устроена так, что фотон остается без массы (часть фотона, обозначенная символом B, и часть, обозначенная W, сокращаются; они также скрыты в символе D), а поскольку поле глюона (G) нигде не встречается, у него тоже нет массы. Включение в уравнение поля Хиггса позволило придать частицам массу, не нарушив при этом калибровочную симметрию. Вместо этого масса частиц возникает в результате их взаимодействия с фоновым полем Хиггса. В этом и состоит красота идеи: мы можем получить массу, не теряя калибровочную симметрию. Четвертая строка основного уравнения — место, в котором поле Хиггса генерирует массу для оставшихся частиц материи стандартной модели.
В этой фантастической картине есть одна загвоздка: ни один эксперимент еще не смог обнаружить частицу Хиггса. Все остальные частицы стандартной модели были выявлены в ходе экспериментов, так что бозон Хиггса — недостающая часть головоломки. Если он действительно существует, как было предсказано, то стандартная модель снова одержит победу и сможет включить объяснение происхождения массы во впечатляющий список своих достижений. Подобно взаимодействиям всех остальных частиц, стандартная модель точно определяет, как частица Хиггса должна проявляться в ходе экспериментов. Единственное, чего стандартная модель нам не говорит, — какова масса этой частицы. Однако мы знаем массу частицы W и верхнего кварка, так что теория позволяет оценить диапазон, в котором находится масса частицы Хиггса. Большой электрон-позитронный коллайдер мог бы увидеть бозон Хиггса, если бы его масса находилась в более легкой части прогнозируемого диапазона. Но поскольку на этом коллайдере частицу Хиггса так и не удалось обнаружить, можно сделать предположение, что она слишком тяжела, чтобы получить ее на БЭПК (не забывайте, согласно уравнению E = mc2 для создания более тяжелых частиц требуется больше энергии). Во время написания этих строк коллайдер Tevatron, расположенный в Национальной лаборатория ускорителей имени Ферми (Fermilab) неподалеку от Чикаго, пытается выявить частицу Хиггса, но пока безрезультатно. Вполне возможно, что у коллайдера Tevatron также недостаточно энергии для того, чтобы получить четкий сигнал о существовании частицы Хиггса, хотя он и принимает активное участие в ее поисках. Большой адронный коллайдер — самый мощный ускоритель среди всех когда-либо построенных. Он действительно должен решить вопрос существования бозона Хиггса, поскольку его энергия намного превышает верхний предел энергии, указанный стандартной моделью. Немного ниже мы объясним, почему так уверены в том, что БАК выполнит задачу, которую не смогли решить его предшественники, но сначала хотели бы объяснить, как именно предполагается получать частицы Хиггса в БАК.
Большой адронный коллайдер построен в том же 27-километровом кольцевом тоннеле, который использовался для БЭПК, однако, кроме самого тоннеля, все остальное изменилось. Совершенно новый ускоритель занимает теперь ту площадь, которую когда-то занимал БЭПК. Этот ускоритель способен разгонять по тоннелю в противоположных направлениях протоны до энергии, более чем в 7 тысяч раз превышающей их энергию массы. Благодаря возможности сталкивать протоны друг с другом на уровне таких энергий физика элементарных частиц вступает в новую эру, и если стандартная модель справедлива, это приведет к образованию множества частиц Хиггса. Протоны состоят из кварков, поэтому, если мы хотим понять, что должно произойти в БАК, все, что нам нужно, — определить соответствующие диаграммы Фейнмана.
Самые важные вершины, соответствующие взаимодействиям между обычными частицами стандартной модели и бозоном Хиггса, показаны на рис. 22, где частица Хиггса, изображенная точечным пунктиром, вступает во взаимодействие с самым тяжелым кварком — истинным кварком (обозначенным как t), а также с достаточно тяжелыми частицами W и Z. Пожалуй, вряд ли стоит удивляться тому, что частица, которая отвечает за происхождение массы, предпочитает вступать во взаимодействие с самыми массивными частицами. Зная, что протоны представляют собой источник кварков, наша задача — найти способ внедрения вершины частицы Хиггса в более крупную диаграмму Фейнмана. После этого мы сможем понять, как в БАК могут образоваться бозоны Хиггса. Поскольку кварки взаимодействуют с бозонами W (или Z), не составляет труда определить, как бозоны Хиггса могут быть образованы с помощью частиц W (или Z). Результат показан на рис. 23: кварки, полученные от каждого из сталкивающихся протонов (обозначенных как p), испускают частицу W (или Z), затем эти частицы сливаются воедино и образуют бозон Хиггса. Считается, что этот процесс, названный слиянием промежуточных бозонов, станет ключевым процессом, протекающим в БАК.
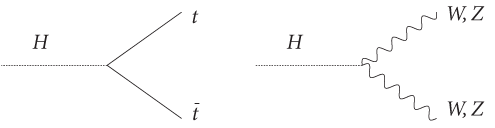
Рис. 22
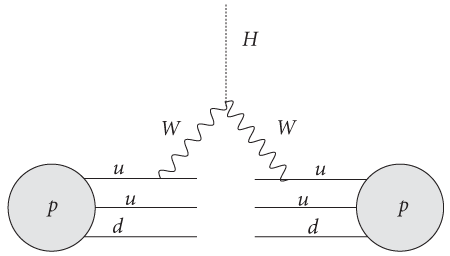
Рис. 23
Механизм образования истинного кварка немного сложнее. Истинных кварков в протонах нет, поэтому нам необходимо найти способ перейти от легких (верхних или нижних) кварков к истинным. Так вот, истинные кварки взаимодействуют с более легкими кварками посредством сильного взаимодействия — другими словами, с помощью испускания и поглощения глюона. Результат показан на рис. 24. Этот процесс очень напоминает процесс слияния промежуточных бозонов, за исключением того, что здесь место частиц W и Z занимают глюоны. В действительности, поскольку этот процесс осуществляется посредством сильного взаимодействия, он представляет собой самый вероятный способ образования бозонов Хиггса в БАК, известный как слияние глюонов.
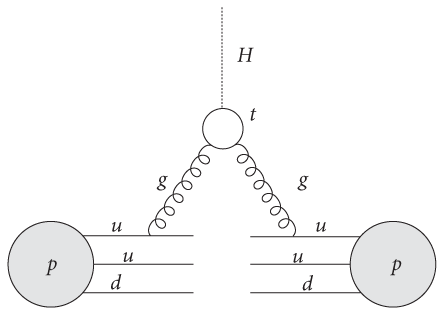
Рис. 24
В настоящее время механизм Хиггса представляет собой общепризнанную теорию происхождения массы во Вселенной. Если все пойдет по плану, БАК либо подтвердит, либо опровергнет принятое в стандартной модели описание происхождения массы. Именно это делает несколько следующих лет волнующим периодом для физиков. Мы находимся в классической научной ситуации, когда есть теория, прогнозирующая, что именно должно произойти в ходе эксперимента, а значит, по его результатам она либо уцелеет, либо погибнет. Но что, если стандартная модель ошибочна? Не может ли случиться нечто совершенно иное и непредвиденное? Ведь не исключено, что она не совсем точна и нет никакой частицы Хиггса. Безусловно, такой сценарий возможен. Специалисты по физике элементарных частиц особенно взволнованны, поскольку знают, что БАК должен открыть нечто новое. Вероятность того, что это не произойдет, вообще не рассматривается, поскольку без бозона Хиггса стандартная модель абсолютно не имеет смысла на уровне энергий, которые способен генерировать БАК, а прогнозы стандартной модели в таком случае просто рассыплются в прах; БАК — первый коллайдер, который проникнет в эту неисследованную область. Строго говоря, если две частицы W сталкиваются друг с другом при энергиях, в тысячу раз превышающих энергию массы протона (что определенно происходит в БАК), то, просто выбросив частицы Хиггса из основного уравнения, мы потеряем возможность расчета происходящего. Включение частиц Хиггса в уравнение делает такие расчеты рабочими, но есть и другие способы рассеяния частиц W, так что механизм Хиггса — не единственный вариант. Какой бы способ ни выбрала Вселенная, БАК абсолютно неизбежно зафиксирует нечто содержащее такие физические явления, с которыми мы еще никогда не сталкивались. Ученым очень редко удается проводить эксперименты с явной гарантией того, что в их ходе будет обнаружено нечто интересное. Именно это делает эксперименты в БАК самым ожидаемым событием за многие годы.

