Глава 1

1. Хотелось бы порекомендовать учителям книгу преподавателя психологии Тимоти Уилсона «Новое направление» (Redirect), подчеркивающую важность сюжета о продвижении от неудачи к успеху (Wilson 2011). Одна из главных задач этой книги — помочь студентам изменить собственный «внутренний сюжет». Непревзойденный автор, описывающий большую роль перемен в настрое мышления, — Кэрол Дуэк 2013.
2. Sklar et al. 2012; Root-Bernstein and Root-Bernstein 1999, chap. 1.

Глава 2

1. Andrews-Hanna 2012; Raichle and Snyder 2007; Takeuchi et al. 2011. Более общие сведения о состоянии покоя см. в: Moussa et al. 2012. В работе, посвященной другой линии исследования, Брюс Манган отмечает, что Уильям Джеймс при описании периферийного сознания упоминает следующую черту: «Существует “перемена” сознания, при которой периферия ненадолго, но часто выходит на передний план и начинает доминировать над центром внимания» (Cook 2002: 237; Mangan 1993).
2. Immordino-Yang et al. 2012.
3. Эдвард де Боно — гроссмейстер по изучению креативности, предложенные им термины «вертикальное» и «латеральное» мышление примерно соответствуют моим терминам «сфокусированное» и «рассеянное» мышление (де Боно, 2012).

   Внимательные читатели заметят мое упоминание того, что рассеянное мышление порой действует в фоновом режиме, при активном сфокусированном состоянии. Однако результаты исследований показывают, что нейронная сеть пассивного режима работы мозга (являющегося всего лишь одним из многих состояний покоя) успокаивается при активном сфокусированном состоянии. Так что же это? Как человеку и преподающему, и изучающему науки, мне кажется, что некоторая несфокусированная деятельность может продолжаться в фоновом режиме при сфокусированной работе, если сфокусированное внимание уведено из зоны интереса. Таким образом, в некотором смысле мое использование термина «рассеянный режим» может скорее пониматься как «деятельность в несфокусированном состоянии, направленная на обучение», а не просто «сеть пассивного режима работы мозга».

4. Существуют также тесные связи с более далекими зонами мозга, как мы увидим далее в аналогии с вниманием-осьминогом.
5. Рассеянное мышление может быть также связано с префронтальными участками, однако оно, вероятно, имеет больше общих связей и отфильтровывает меньше нерелевантных связей.
6. Психолог Норман Кук предположил, что «первый элемент центрального принципа человеческой психологии может быть определен как поток информации между: 1) правым и левым полушариями и 2) «доминантными» [левополушарными] и периферийными эффекторными механизмами, используемыми для вербального общения» (Cook 1989: 15). Однако также стоит отметить, что разница между полушариями часто становилась основой для бесчисленных необоснованных экстраполяций и неверных выводов (Efron 1990).
7. Согласно исследованиям занятости студентов (2012), учащиеся вузов, изучавшие инженерные специальности, проводили больше всего времени за занятиями: старшекурсники в среднем тратили на подготовку к занятиям 18 часов в неделю, старшекурсники педагогических специальностей — 15 часов, старшекурсники, изучающие общественные науки и бизнес, — около 14 часов. В статье, опубликованной в The New York Times под заголовком «Почему студенты-естественники меняют специальность (потому что сложно учиться)», преподаватель инженерных наук Дэвид Голдберг отмечает, что серьезные требования по математике, физике и химии могут привести к тому, что студенты будут выбывать из «гонки на выживание под знаменем математики и естественных наук» (Drew 2011).
8. Об эволюционных аспектах математического мышления см. в: Geary 2005, chap. 6.

   Разумеется, многие абстрактные термины не связаны с математикой. Однако поразительное количество таких типов абстрактных идей относится к эмоциям. Мы можем не видеть эти термины, но чувствуем их или по меньшей мере их важные стороны.

   Терренс Дикон, автор книги «Символический вид» (The Symbolic Species), отмечает неотъемлемую сложность проблемы кодирования/декодирования в математике:

   «Вообразите, что вы впервые сталкиваетесь с новым видом математических понятий — например, рекурсивным вычитанием (т.е. делением). Когда детям преподают это абстрактное понятие, чаще всего их заставляют выучить набор правил обращения с действиями и числами. а потом эти правила снова и снова отрабатываются с разными числами в надежде, что такая практика поможет детям “увидеть” параллели с определенными физическими проявлениями. Мы часто описываем это как обучение математическим действиям путем механического заучивания (что в моих терминах называется индексальным обучением), а затем, когда действия уже могут совершаться почти бессознательно, мы надеемся, что дети осознают, как математика соотносится с процессами физического мира. На определенном этапе, если все идет как нужно, дети “понимают” общий абстрактный принцип, объединяющий эти связанные с символами и формулами операции. Так они могут реорганизовать то, что уже заучили механически, в соответствии с мнемоническими принципами более высокого уровня, касающимися комбинаторных возможностей и их абстрактной соотнесенности с манипулированием объектами. Такой шаг к абстракции для многих детей зачастую сложен. Однако вспомните, что та же трансформация на еще более высоком уровне абстракции требуется для понимания высшей математики. Дифференциалы связаны с рекурсивным делением, интегралы — с рекурсивным умножением, в каждом случае до бесконечности, т.е. до предельных величин (это возможно потому, что они зависят от сходящихся рядов, которые сами по себе плод умозаключений, а не прямого наблюдения). Эта способность видеть, что будет, если операцию повторять бесчисленное количество раз, и является ключевой для того, чтобы разрешить парадокс Зенона (который, кажется, невозможно осмыслить, когда он описан словами). Однако вдобавок к этой сложности используемый сейчас нами лейбницевский формализм сводит эту бесконечную рекурсию к одному символу (dx/dt) или знаку интеграла, поскольку никто не в состоянии писать такие операции бесконечно. Из-за этого манипулирование математическими символами еще больше теряет связь с соответствующими физическими величинами.

   Поэтому смысл операции, выраженный математически, по сути содержит двойную кодировку. Да, у нас развиты мыслительные способности, позволяющие манипулировать с физическими объектами, и, разумеется, это сложно. Однако математика есть форма «кодирования», а не только воспроизведения, и декодирование является чрезвычайно трудным процессом именно из-за комбинаторных сложностей. Вот почему кодирование и шифрование осложняют восстановление и получение изначальной информации. По моему мнению, это является неотъемлемым свойством математики, независимо от развитых у нас способностей. Математика сложна по той же причине, по которой сложна расшифровка закодированного послания.

   К моему удивлению, мы все знаем, что математические уравнения — это по сути зашифрованные послания, для расшифровки которых нужен ключ. Однако мы почему-то изумляемся, что высшая математика так сложна для преподавания, и часто виним систему образования или преподавателей. Мне кажется, что с тем же успехом можно обвинять всю эволюцию» (личная переписка с автором, 11 июля 2013 г.).

9. Bilalič et al. 2008.
10. Geary 2011. См. также документальный фильм «Частная вселенная» (A Private Universe) по адресу , который обусловил дальнейшее изучение природы ошибочного понимания естественно-научных концепций.
11. Алан Шёнфилд (Alan Schoenfeld 1992) замечает, что более сотни имеющихся в его распоряжении видеороликов, на которых старшеклассники и студенты решают незнакомые задачи, свидетельствуют: примерно в 60% случаев решения основываются на подходе «прочти, быстро выбери способ и не отступайся от него ни под каким видом». Это характерный пример того, как работает сфокусированное мышление.
12. Голдакр, 2010.
13. Gerardi et al. 2013.
14. Различия между полушариями головного мозга могут быть важны, однако, как уже упоминалось, все утверждения в этой области нужно принимать с осторожностью. Лучше всего сказал об этом Норман Кук: «Многие идеи, высказанные в ходе дебатов 1970-х годов, ощутимо выходили за пределы фактических знаний: разницей между полушариями объяснялись сразу все загадки человеческой психологии, включая подсознание, природу творчества и парапсихологические феномены, — однако неизбежное отклонение маятника в обратную сторону было также чрезмерным» (Cook 2002: 9).
15. Demaree et al. 2005; Gainotti 2012.
16. McGilchrist 2010; Mihov et al. 2010.
17. Nielsen et al. 2013.
18. Другой вариант задачи см. у де Боно (де Боно, 2012) — это дало толчок к созданию приведенной здесь задачи. Классическая книга де Боно содержит огромное количество таких задач и может служить отличным чтением.
19. Immordino-Yang et al. 2012.
20. Я говорю о чередовании сфокусированного и рассеянного мышления, хотя аналогичный процесс происходит и при перемещении информации между полушариями мозга. Примерное представление о том, как информация переходит от одного полушария к другому и обратно, дают эксперименты над курами. Научиться не клевать горькие зерна — процесс сложной обработки следов памяти, передающихся от полушария к полушарию в течение нескольких часов (Güntürkün 2003).

    Анке Баума отмечает: «Наблюдаемый шаблон латерализации не означает, что на всех стадиях, требуемых определенной задачей, превалирует одно и то же полушарие. Существуют указания на то, что [правое полушарие] может доминировать на одной стадии обработки информации, а [левое полушарие] — на другой стадии. То, какое полушарие окажется главным при решении конкретной задачи, определяется относительной сложностью конкретной стадии обработки информации» (Bouma 1990: 86).

21. Передвиньте монеты так, как показано на рисунке: видите ли вы теперь треугольник вершиной вниз?

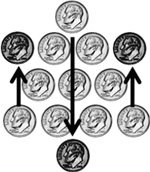
Глава 3

1. Модель функционального пространства мозга, разработанная Марселем Кинсбурном и Меррилл Хискок (Kinsbourne, Hiscock 1983), предполагает, что одновременно выполняемые действия «мешают» друг другу тем больше, чем меньше расстояние между центрами мозга, ответственными за эти функции. Две задачи, одновременно обрабатываемые одним полушарием мозга, и в частности одним и тем же участком мозга, могут осложнить процесс (Bouma 1990: 122). Возможно, рассеянное мышление имеет больше возможности одновременно справляться с несколькими задачами, поскольку рассеянные процессы имеют расфокусированную природу.
2. Rocke 2010: 316, цит. по: Gruber 1981.
3. Ibid., p. 3–4.
4. Kaufman et al. 2010, в частности гипотеза на с. 222–224; Takeuchi et al. 2012.
5. В попытках отследить происхождение этой легенды я списалась с Леонардом ДеГраафом, архивариусом Исторического парка Томаса Эдисона. Он ответил: «Я слышал историю о шарикоподшипнике, но никогда не видел документов, ее подтверждающих. Я едва ли могу сказать что-то конкретное о происхождении этой легенды. Возможно, эти рассказы в некоторой степени основаны на реальности, но стали частью мифологии Эдисона».
6. Dalí 1948: 36.
7. Gabora and Ranjan 2013: 19.
8. Christopher Lee Niebauer and Garvey 2004. Нибауэр упоминает различие между объектным и многоуровневым мышлением. Третья, парадоксальная ошибка в предложении состоит в том, что третьей ошибки нет.
9. Kapur and Bielczyc 2012 содержит отличный обзор с упором на важность неудачи при решении задач.
10. Прекрасное обсуждение многих вариантов того, что Эдисон мог сказать или написать, см. здесь: /
11. Andrews-Hanna 2012; Raichle and Snyder 2007.
12. Дуг Рорер и Харолд Пашлер (Rohrer and Pashler 2010: 406) отмечают: «…недавний анализ временной динамики изучения материала показывает, что знания более прочны в том случае, если занятия распределены так, что весь период обучения длится дольше, чем принято». Каким образом это соотносится с чередованием сфокусированного и расслабленного мышления — важная тема для будущих исследований. См.: Immordino-Yang et al. 2012. Иными словами, описанная мной картина — здравое предположение о процессах, происходящих при обучении, однако оно требует дополнительных исследований.
13. Baumeister and Tierney 2011.
14. Отдельно отмечаю, что эти утверждения о стимулах, способных активизировать рассеянный режим мышления, — только мои догадки, основанные на знании о том, как к людям приходят некоторые наиболее творческие озарения.
15. Bilalič et al. 2008.
16. Nakano et al. 2012.
17. Kounios and Beeman 2009: 212.
18. Dijksterhuis et al. 2006.
19. Кратковременная память содержит активизированную информацию, которая не находится в режиме активного повторения. Рабочая память — подвид кратковременной памяти и содержит информацию, которая находится в фокусе внимания и в стадии активной обработки (Baddeley et al. 2009).
20. Cowan 2001.
21. Если вас интересует нейронная география, лежащая в основе всего описываемого, то дело выглядит так, будто долговременная и рабочая память используют пересекающиеся области лобной и теменной зон. Средняя височная зона используется только для долговременной, но не для рабочей памяти. См.: Guida et al. 2012: 225–226; Dudai 2004.
22. Baddeley et al. 2009: 71–73; Carpenter et al. 2012. Интервальные повторения также известны как «распределенная практика». Dunlosky et al. 2013, sec. 9, дает отличный обзор по теме распределенной практики. К сожалению, как отмечено в Rohrer and Pashler 2007, многие преподаватели, особенно математики, полагают, что заниматься усиленно и длительно — хороший способ усвоить знания надолго, поэтому студентам дается большое количество задач одинакового типа, которые в результате сводятся к рутинным действиям и не дают ощутимого долгосрочного эффекта.
23. Xie et al. 2013.
24. Stickgold and Ellenbogen 2008.
25. Ji and Wilson 2006; Oudiette et al. 2011.
26. Ellenbogen et al. 2007. Рассеянное мышление также может относиться к низкому латентному торможению, т.е. к невнимательности и повышенной отвлекаемости (Carson et al. 2003). Для тех из нас, чьи мысли меняются в середине фразы, есть творческая надежда!
27. Erlacher and Schredl 2010.
28. Wamsley et al. 2010.

Глава 4

1. Лурия, 1968.
2. Beilock 2010: 151–154.
3. Дети учатся посредством сфокусированного внимания, но используют и рассеянный режим с минимальным контролем, чтобы получать знания даже в отсутствие сфокусированного внимания (Thompson-Schill et al. 2009). Иными словами, сфокусированное мышление нужно детям меньше, чем взрослым при изучении нового языка, — возможно, поэтому маленькие дети так легко усваивают иностранный язык. Однако в более позднем возрасте для изучения языка требуется сфокусированный режим хотя бы в небольших количествах.
4. Guida et al. 2012, sec. 8. Недавно Синь Цзинь, Фатуэл Текуапетла и Руй Коста обнаружили, что нейроны базальных ганглиев играют важную роль при преобразовании цепи отдельных элементов в последовательность поведения, — это суть формирования порций информации (Jin et al. 2014). Руй Коста получил грант на €2 млн для изучения механизма формирования порций информации — посмотрим, что он обнаружит!
5. Brent and Felder 2012; Sweller et al. 2011, chap. 8.
6. Алессандро Гуида (Guida 2012: 235) с коллегами отмечал, что формирование порций информации, по всей видимости, изначально опирается на рабочую память, связанную с префронтальными участками, и является результатом сфокусированного внимания, что помогает формировать порции информации. Такие порции при накапливании опыта начинают оседать в долговременной памяти, соотносящейся с теменными зонами. Отдельный аспект памяти связан с нейронными колебательными ритмами, которые помогают связать перцептуальную и контекстуальную информацию из многих участков мозга (Nyhus and Curran 2010). См.: Cho et al. 2012 — исследование развития беглости вспоминания при решении арифметических задач у детей.
7. Baddeley et al. 2009, chap. 6; Cree and McRae 2003.
8. Baddeley et al. 2009: 101–104.
9. «Общая картина» и «общий взгляд», упомянутые мной, могут рассматриваться как когнитивный шаблон. См.: Guida et al. 2012, в частности раздел 3.1. Шаблоны, возникающие при изучении математики и естественных наук, естественным образом тяготеют к большей аморфности, чем возникающие при игре в шахматы. Автор отмечает, что порции информации формируются очень быстро, однако шаблоны, связанные с функциональной реорганизацией, требуют времени — от пяти недель и больше (Guida et al. 2012). См. также обсуждение в Cooper and Sweller 1987; Mastascusa et al. 2011: 23–43. Для понимания этих идей, относящихся к приобретению опыта, также полезна дискуссия в Bransford et al. 2000, chap. 2. Предварительные знания способны помочь при изучении нового материала, однако могут и мешать, поскольку устоявшиеся схемы перестроить труднее. Это особенно заметно в отношении устоявшихся — и обычно трудно изменяемых — ошибочных представлений студентов об основных понятиях физики (Hake 1998; Halloun and Hestenes 1985). Как замечают Пол Пинтрич и коллеги (Pintrich 1993: 170), «у учащегося возникает парадокс: существующие понятия, с одной стороны, это потенциальная инерция, сопротивляющаяся концептуальным переменам, с другой стороны, они также дают основу, которую учащийся может использовать для интерпретации и понимания новой, потенциально конфликтующей информации».
10. Geary et al. 2008: 4–7; Karpicke 2012; Karpicke et al. 2009; Karpicke and Grimaldi 2012; Kornell et al. 2009; Roediger and Karpicke 2006. Обзоры см. в: McDaniel and Callender 2008; Roediger and Butler 2011.
11. Karpicke et al. 2009: 471. См также эффект Даннинга–Крюгера, когда некомпетентные люди ошибочно завышают свои способности. Dunning et al. 2003; Kruger and Dunning 1999; Ehrlinger et al. 2008; Bursonet et al. 2006.
12. Baddeley et al. 2009: 111.
13. Dunlosky et al. 2013, sec. 4.
14. Longcamp et al. 2008.
15. Dunlosky et al. 2013, sec. 7.
16. См., в частности, Guida et al. 2012, где описано, как эксперты учатся использовать долговременную память для расширения рабочей. См. также: Geary et al. 2008: 4–5, где замечено: «Объем рабочей памяти ограничивает успехи в математике, однако эти ограничения можно преодолеть практикой, когда процесс доводится до автоматизма».
17. Анаграмма — «madame Curie». Автором считается Мейран Краус (Meyran Kraus), .
18. Джеффри Карпик с коллегами (Karpicke 2009) предполагает наличие связи между иллюзиями компетентности при обучении и трудностями с анаграммами в тех случаях, когда ответ очевиден, в противоположность случаям, когда он не ясен.
19. Генри Рёдигер и Мери Пик (Roediger and Pyc 2012: 243) отмечают: «Учителей и преподавателей часто заботит вопрос креативности учащихся. Рекомендуемые нами методы показывают улучшения в процессе получения и сохранения знаний об основных понятиях и фактах, хотя некоторые критикуют такой подход, называя его “зубрежкой” и “прямым запоминанием”, а не творческим синтезом. Разве цель образования — не культивировать в учениках любознательность, стремление к открытиям и креативность? Мы не оспариваем креативность, но утверждаем, что предпосылкой к креативности служат прочные знания в определенной области. Студенты вряд ли будут способны к творческим открытиям в рамках какого бы то ни было предмета без обширного набора фактов и концепций, находящихся в их полном распоряжении. Заучивание понятий и фактов и творческое мышление не обязательно конфликтуют, они находятся в симбиозе».
20. Geary 2005, chap. 6; Джонсон, 2013.
21. Джонсон, 2013.
22. Simonton 2004: 112.
23. Это моя собственная формулировка общепринятого в научных кругах мнения. Сантьяго Рамон-и-Кахаль отмечал (цитирую Эмиля Дюкло): «Шанс открывается не тому, кто его желает, а тому, кто его заслуживает». И далее: «В науке, так же как в лотерее, удача благоволит к тем, чья ставка больше, — или, по другой аналогии, к тем, кто постоянно возделывает свой сад» (Ramón y Cajal 1999: 67–68). Луи Пастер писал: «В сфере научных наблюдений удача благоволит только сведущим и хорошо подготовленным умам». Аналогичный подход отражен в латинской пословице «Фортуна любит смелых» и в девизе британских парашютно-десантных частей особого назначения (SAS): «Побеждает отважный».
24. Kounios and Beeman 2009 [1897]; Ramón y Cajal 1999: 5.
25. Rocke 2010.
26. Thurston 1990: 846–847.
27. См. основополагающую работу Карла Андерса Эрикссона о совершенствовании мастерства (Ericsson 2009). Ценные популярные подходы, относящиеся к развитию таланта, см. в: Койл, 2011; Грин, 2014; Leonard 1991.
28. Karpicke and Blunt 2011a; Karpicke and Blunt 2011b. Дальнейшую информацию см. в: Guida et al. 2012: 239.
29. Интересно, что префронтальные зоны левого полушария бывают активны во время кодирующей фазы запоминания, а зоны правого полушария — во время вспоминания. Об этом сообщают разные группы, использовавшие различные методы получения изображений мозга (Cook 2002: 37). Возможно, извлечение запомненного материала приводит к образованию связей, свойственных рассеянному режиму? См. также: Geary et al. 2008: 4–6 до 4–7.
30. Здесь есть и опасности. Например, что, если студента попросят вспомнить материал, чтобы определить, что должно быть включено в концепт-карту? Несомненно, различия между учебными предметами тоже имеют значения. В случае ряда дисциплин, например связанных с передачей сигнала внутри биологических клеток, концепт-карты естественным образом более удобны при усвоении ключевых идей.
31. Brown et al. 1989.
32. Джонсон, 2013.
33. Baddeley et al. 2009, chap. 8.
34. Кен Кёдингер, преподающий человеко-компьютерное взаимодействие и психологию в Университете Карнеги–Меллон, пишет: «Чтобы максимизировать удержание материала в памяти, лучше всего поначалу давать студентам информацию через небольшие промежутки, а затем постепенно удлинять промежуточные периоды. Разные типы информации — например, абстрактные понятия в противоположность конкретным фактам — требуют разных режимов запоминания» (цит. по: Paul 2012).
35. Dunlosky et al. 2013, sec. 10; Roediger and Pyc 2012; Taylor and Rohrer 2010.
36. Rohrer and Pashler 2007.
37. По-видимому, массово используемые методы презентации материала создают иллюзию компетентности при преподавании. Студенты быстро запоминают материал, однако, как показали исследования, забывают они его тоже быстро. Рёдигер и Пик (Roediger and Pyc 2012: 244) отмечают: «Такой исход показывает, почему преподаватели и студенты по заблуждению используют методики, которые оказываются неэффективными в долгосрочной перспективе. Когда мы учим материал, мы настолько сосредоточены на процессе заучивания, что с удовольствием прибегаем к стратегиям, облегчающим запоминание. Массовые практики именно к этому и приводят. Чтобы материал лучше и дольше удерживался в памяти, нужно использовать интервальное и чередующееся повторение, однако во время заучивания эта процедура кажется трудной. Чередование осложняет изначальный процесс обучения, однако оно более желательно из-за того, что способствует более надежному и длительному сохранению материала в памяти».
38. Rohrer et al. 2013.
39. Рорер и Пашлер (Rohrer and Pashler 2010: 406) отмечают: «…чередование разных типов задач (так редко встречающееся в математике и естественных науках) заметно облегчает усвоение материала».
40. Личная переписка с автором, 20 августа 2013 г. См. также: Carey 2012.
41. Longcamp et al. 2008.
42. Например, см.: http://usefulshortcuts.com/alt-codes.

Глава 5

1. Emsley 2005: 103.
2. Chu and Choi 2005; Graham 2005; Partnoy 2012.
3. Стил (Steel 2007: 65) отмечает: «По некоторым оценкам, 80–95% студентов колледжей занимаются прокрастинацией… примерно 75% считают себя прокрастинаторами… и почти 50% прокрастинируют постоянно и испытывают из-за этого проблемы. Абсолютное количество прокрастинаторов довольно значительно; студенты сообщают, что прокрастинация в стандартном случае занимает одну треть активного времени дня, часто они отвлекаются на сон, игры или просмотр телевизионных программ… Более того, этот процент растет… Прокрастинация, обычно процветающая в высших учебных заведениях, также широко распространена среди прочего населения и стабильно проявляется у 15–20% взрослых».
4. Ainslie and Haslam 1992; Steel 2007.
5. Lyons and Beilock 2012.
6. Эмметт, 2008.
7. См. в работе Дахигг, 2014, где цитируется Weick 1984.
8. Роберт Бойс (Robert Boice 1996: 155) отмечал, что прокрастинация связана с сужением поля сознательного восприятия. См. также с. 118–119.
9. Boice 1996: 176.
10. Tice and Baumeister 1997.
11. Boice 1996: 131.

Глава 6

1. McClain 2011; Wan et al. 2011.
2. Дахигг, 2014.
3. Steel 2010: 190, со ссылкой на Oaten and Cheng 2006 and Oaten and Cheng 2007.
4. Baumeister and Tierney 2011: 43–51.
5. Steel 2010, со ссылкой на оригинальную работу Robert Eisenberger 1992, и др.
6. Ibid., p. 128–130, в свою очередь с отсылкой к Gabriele Oettingen.
7. Beilock 2010: 34–35.
8. Ericsson et al. 2007.
9. Boice 1996: 18–22.
10. Paul 2013.

Глава 7

1. Важно понимать, что значительная часть литературы об экспертах касается людей, которые годами вырабатывали нужный уровень мастерства. Однако это эксперты и мастерство другого уровня. Например, если вы знаете аббревиатуры FBI и IBM, то проще запомнить последовательность как две порции информации, а не как разрозненный набор из шести букв. Однако такой легкий способ формирования порций информации предполагает, что вы уже знаете не только значения FBI и IBM, но и латинский алфавит. Представьте, насколько сложнее было бы запомнить последовательность тибетских букв .

   При изучении математики и естественных наук мы начинаем с некоторого уровня владения материалом, и затем ожидается, что наш прогресс в течение семестра будет ничем не похож на прыжок от неопытного новичка до шахматного гроссмейстера. Когда вы изучаете какой-то учебный предмет, за один семестр не происходит серьезных нейронных перемен, аналогичных трансформации новичка в гроссмейстера. Однако существуют некоторые указания на то, что нейронные различия при обработке материала могут быть заметны даже на протяжении двух недель (Guida et al. 2012). В частности, авторы отмечают, что эксперты широко используют височные зоны, важные для долговременной памяти (Guida et al. 2012: 239). Иными словами, когда мы отвлекаем студентов от формирования структур долговременной памяти, мы осложняем им процесс обретения мастерства. Разумеется, сосредоточение исключительно на запоминании без применения творческого подхода тоже может привести к проблемам. Напоминаю: любой метод преподавания может быть применен неверно, зато разнообразие (не говоря уже о компетентности) — главное в нашем деле.

2. Мы говорили о чередовании разных методик при изучении одной и той же темы. А как насчет чередования совершенно различных учебных предметов? К сожалению, по этому вопросу пока нет исследовательской литературы (Roediger and Pyc 2012: 244), поэтому в этом отношении я предлагаю ориентироваться на здравый смысл и общую практику. Будет интересно посмотреть на будущие исследования по этой теме.
3. Kalbfleisch 2004.
4. В работе Guida et al. 2012: 236–237 отмечается, что порции информации в рабочей и, соответственно, в долговременной памяти «растут с практикой и мастерством… порции также становятся богаче, поскольку с каждой из них ассоциируется большее количество опыта, касающегося долговременной памяти. Более того, несколько порций информации долговременной памяти могут оказаться привязаны к знанию. Со временем, если человек становится экспертом, наличие связок между несколькими порциями может привести к созданию порций высокого иерархического уровня… Например, при игре в шахматы шаблоны могут иметь связку с… “планами, ходами, стратегическими и тактическими концепциями, а также с другими шаблонами”… Мы предполагаем, что функциональная реорганизация мозга может иметь место при обретении мастерства в случаях, когда порции информации долговременной памяти и структуры знания существуют и являются эффективными в рамках мастерства».
5. Duke et al. 2009.
6. Хороший обзор условий, при которых намеренная практика наиболее эффективна, см. в Pachman et al. 2013.
7. Roediger and Karpicke 2006: 199.
8. Wan et al. 2011. Это исследование было призвано описать нейронные цепочки, отвечающие за быстрое (до двух секунд) интуитивное определение наилучшего варианта следующего хода в сёги — сложнейшей стратегической игре. Часть мозга, связанная с быстрыми, неявными, бессознательными привычками (цепь между предклиньем и хвостатым ядром), оказалась главной для быстрой генерации наилучшего варианта следующего хода у профессиональных игроков. См. также: McClain 2011.
9. Charness et al. 2005.
10. Karpicke et al. 2009; McDaniel and Callender 2008.
11. Fischer and Bidell 2006: 363–370.
12. Roediger and Karpicke 2006, со ссылкой на William James’s Principles of Psychology.
13. Beilock 2010: 54–57.
14. Karpicke and Blunt 2011b; Mastascusa et al. 2011, chap. 6; Pyc and Rawson 2010; Roediger and Karpicke 2006; Rohrer and Pashler 2010. В обзоре различных учебных методов (Dunlosky et al. 2013) отмечается крайняя полезность «тренировочного тестирования» из-за его эффективности, широкой применимости и легкости использования. См. также: Pennebaker et al. 2013.
15. Keresztes et al. 2013 дает свидетельства тому, что тестирование улучшает усвоение материала в долгосрочной перспективе путем стабилизации активизирующих шаблонов на большом количестве зон головного мозга.
16. Pashler et al. 2005.
17. Dunlosky et al. 2013, sec. 8; Karpicke and Roediger 2008; Roediger and Karpicke 2006.

Глава 8

1. Аллен, 2011.
2. Steel 2010: 182.
3. Beilock 2010: 162–165; Chiesa and Serretti 2009; Lutz et al. 2008.
4. Те, кто заинтересуется, могут обратиться к ресурсам, перечисленным на http://www.acmhe.org/
5. Boice 1996: 59.
6. Феррис, 2013.
7. Ibid., p. 487.
8. Фьоре, 2013.
9. Scullin and McDaniel 2010.
10. Newport 2012; Newport 2006.
11. Фьоре, 2013.
12. Baddeley et al. 2009: 378–379.

Глава 9

1. Johansson 2012, chap. 7.
2. Boice 1996: 120; Фьоре, 2013, chap. 6.
3. Ibid., p. 125.
4. Amabile et al. 2002; Baer and Oldham 2006; Boice 1996: 66.
5. Rohrer, et al. (в прессе).
6. Chi et al. 1981.
7. Noesner 2010.
8. Newport 2012, особенно гл. 1 (“Rule#1”).
9. Nakano et al. 2012.
10. Duhigg, 2012.
11. Newport 2012.
12. Многие из таких идей см. у Edelman 2012.

Глава 10

1. Эленор Магуайр с коллегами (Maguire et al. 2012) изучала известных мнемонистов в ходе таких мероприятий, как Мировой чемпионат по запоминанию. «Используя нейрофизиологические измерения, а также структурную и функциональную томографию», они обнаружили, что «суперпамять не является результатом исключительных мыслительных способностей или структурных отличий мозга. Обладатели суперпамяти скорее использовали пространственные методы усвоения информации, задействуя такие участки мозга, как гиппокамп, принципиальные для памяти, в частности для пространственной памяти».

   Тони Бьюзен сделал многое для того, чтобы мыль о важности приемов запоминания стала достоянием широкой публики. Его книга (Buzan 1991) содержит дальнейшую информацию о некоторых распространенных приемах запоминания.

2. В работе Maguire et al. 2003 отмечается, что приемы запоминания часто считаются слишком сложными для использования, однако некоторые из них, такие как «дворец памяти», вполне понятны и полезны при попытках запомнить важную информацию.
3. Cai et al. 2013; Фоер, 2013. Дениз Кей с коллегами в своей работе показала, что специализация одного полушария (обычно левого) в связи с языками сопровождается аналогичной специализацией другого полушария в связи со зрительно-пространственными способностями. Специализация функции в одном полушарии, иными словами, приводит к специализации другой функции в другом полушарии.
4. Ross and Lawrence 1968.
5. Baddeley et al. 2009: 363–365.
6. http://www.ted.com/talks/joshua_foer_
   feats_of_memory_anyone_can_do.html
7. http://www.skillstoolbox.com/career-and-education-skills/learning-skills/memory-skills/mnemonics/applications-of-mnemonic-systems/how-to-memorize-formulas/
8. О важности пространственных обоснований см. в Kell et al. 2013.

Глава 11

1. Cat 2001 и Lützen 2005 — два источника информации о метафорах, относящихся к физике конца XIX века. О метафорах в химии и других науках см.: Rocke 2010, в частности главу 11. См. также: Gentner and Jeziorski 1993. Тема томографии и визуализации не укладываются в какую-то одну книгу — см., например, Journal of Mental Imagery.
2. Признанный специалист по математическим моделям Эммануэль Дерман отмечает: «Теории описывают мир и взаимодействуют с ним по его собственным законам и потому должны быть самостоятельными. Модели не самостоятельны. Они — метафоры, сравнивающие объект своего внимания с чем-то схожим. Схожесть всегда лишь частична, поэтому модели всегда упрощают реальность и сокращают количество граней многосложного мира… Если коротко, то теории говорят о том, что представляет собой объект, модели — на что он похож» (Derman 2011: 6).
3. Solomon 1994.
4. Rocke 2010: xvi.
5. Ibid., p. 287, со ссылкой на Berichte der Durstigen Chemischen Gesellschaft (1886), p. 3536. Это был пародийный номер несуществующего «durstigen» («жаждущего») общества знатоков и любителей. Выпуск был разослан подписчикам издания, сегодня его практически невозможно найти в силу бутафорского характера.
6. Rawson and Dunlosky 2011.
7. Dunlosky et al. 2013; Roediger and Pyc 2012. В обзоре, касающемся использования карточек студентами (Kathryn Wissman et al. 2012: 568), отмечается: «Студенты понимают выгоды усиленных и упорных занятий (объем практики), но обычно не практикуют или не понимают выгод занятий с более продолжительными интервалами (время практики)».
8. Morris et al. 2005.
9. Baddeley et al. 2009: 207–209.
10. Вы можете счесть, что в этой книге я упомянула все компоненты учебного принципа SQ3R (survey, question, read, recall и review — исследовать, задать вопросы, прочесть, вспомнить, повторить) или также SQ4R (survey, question, read, recite, review, write — исследовать, задать вопросы, прочесть, пересказать, повторить и записать). Поэтому вы можете спросить, почему я не остановилась на этом методе подробнее. Метод SQ3R разработал психолог Фрэнсис Плезант Робинсон в качестве инструмента обучения. Главная часть изучения математики и естественных наук — решение задач, к которому метод SQ3R неприменим. Это отмечено не мной одной. Преподаватель физики Рональд Аарон и его сын Роберт Аарон пишут: «…В одном из психологических текстов предлагается изучение по методу SQ3R… Для усвоения лекций он предлагает метод LISAN [lead, idea, signal words, actively listen, note-taking — идти впереди, схватывать основные идеи, примечать слова-сигналы, активно слушать, вести записи]… Верите ли вы, что эти методы могут вам помочь? Верите ли вы в Санта-Клауса? А в пасхального кролика?» (Aaron and Aaron 1984: 2).
11. Любопытно, что эта сфера малоисследованна, а то немногое, что есть, только подтверждает идею о том, что записывание от руки помогает усваивать информацию лучше, чем если набирать ее на клавиатуре компьютера. См.: Rivard and Straw 2000; Smoker et al. 2009; Velay and Longcamp 2012.
12. Cassilhas et al. 2012; Nagamatsu et al. 2013; van Praag et al. 1999.
13. Guida et al. 2012: 230; Leutner et al. 2009.
14. В работе Levin et al. 1992 показывается, что студенты, использующие мнемонику, успевают лучше студентов, применяющих контекстуальный и вольный подход к запоминанию материала.
15. Гуида (Guida et al. 2012) обращает внимание на то, что хорошее владение методами запоминания может ускорить процесс формирования порций информации и структур знания, тем самым помогая быстрее приобрести опыт и мастерство путем частичного использования долговременной памяти как рабочей.
16. Baddeley et al. 2009: 376–377, со ссылкой на исследования Helga and Tony Noice 2007.

Глава 12

1. Jin et al. 2014.
2. Partnoy 2012: 73. Партной далее пишет: «Иногда точное понимание наших бессознательных действий может уничтожить естественную спонтанность. Если мы слишком осознанно за собой следим, мы мешаем инстинктивному подходу там, где он нужен. Однако, если мы не следим за собой вовсе, мы никогда не усовершенствуем инстинкт. Главное здесь — в течение считаных секунд осознавать те факторы, на которых строится наше решение… но не осознавать их слишком четко, чтобы они не стали неестественными и неэффективными» (Partnoy 2012: 111).
3. Partnoy 2012: 72, со ссылкой на Klein 1999.
4. Klein 1999: 150, со ссылкой на Klein and Klein 1981. Однако обратите внимание на малый объем выборки в Klein and Klein 1981.
5. Авторы работы Mauro Pesenti et al. 2001: 103 пишут: «Мы показали, что высокие способности к исчислениям отнюдь не обусловлены повышенной активностью процессов, происходящих в мозгу у неэкспертов; скорее, дело обстоит так, что эксперты и неэксперты используют для счета разные участки мозга. Мы обнаружили, что эксперты могут переключаться с требующих усилий кратковременных стратегий хранения информации на высокоэффективное эпизодическое кодирование в памяти и воспроизведение, — этот процесс поддерживался правой префронтальной и средней височной зонами мозга».

   Уже в 1899 г. блестящий психолог Уильям Джеймс в своем классическом труде «Беседы с учителями о психологии» писал: «Теперь вы видите, почему зубрежка так бесполезна при обучении. Зубрежка призвана активно вбивать в голову сведения непосредственно перед испытанием. Однако выученный таким образом материал почти не дает ассоциаций. Но то же заучивание — в разные дни и в разных контекстах, с чтением и пересказом, с постоянным повторением, с установлением связей между изучаемым материалом и другими знаниями — оказывается прочно встроенным в структуру сознания. Вот почему нужно побуждать в учениках привычку непрерывно повторять выученное» (William 2008 [1899]: 73).

6. Уильям Чейз и Герберт Саймон в своем классическом исследовании (Chase and Simon 1973) выяснили, что, когда хорошие шахматисты интуитивно определяют для себя следующий ход в партии, этот процесс основан у них на исключительном и быстром просчитывании шаблонов — на умении, развившемся в результате тщательных тренировок. В работе Fernand Gobet et al. 2001: 236 порция информации определяется как «собрание элементов, имеющих крепкие связи друг с другом, но слабо связанных с другими порциями».
7. Amidzic et al. 2001; Elo 1978; Simon 1974. В Gobet and Simon 2000 говорится о 300 000 порциях информации.
8. Gobet 2005. Далее автор замечает, что мастерство в одной области не переходит в другую. Это правда: знание испанского не поможет заказать в кафе тушеную капусту на немецком. Однако метанавыки очень важны. Если вы научились учить один язык, учить второй будет легче.

   В таких случаях также полезно развивать мастерство, например, в шахматах: с его помощью образовывается набор нейронных цепей, аналогичных тем, которые нужны для изучения математики и естественных наук. Даже если нейронные структуры сводятся к чему-нибудь простому вроде «Нужно усвоить правила игры» — это уже ценная информация.

9. Beilock 2010: 77–78; White and Shah 2006.
10. Этот вид открытий очень мало освещен в исследовательской литературе. См.: Simonton 2009.
11. Carson et al. 2003; Ellenbogen et al. 2007; White and Shah 2011.
12. В работе Merim Bilalič et al. 2007 указывается, что некоторые игроки с IQ между 108 и 116 попали в элитную игровую группу благодаря обширной практике. Элитная группа имеет средний IQ 130. См. также: Duckworth and Seligman 2005.

    Нобелевский лауреат Ричард Фейнман любил представлять свой IQ — 125 — как свидетельство того, что можно достичь успеха независимо от показаний тестов на интеллект. Фейнман явно обладал природным умом, однако уже с юности он усиленно занимался физикой и математикой и развивал интуицию (Gleick 1992).

13. Klingberg 2008.
14. Silverman 2012.
15. Felder 1988. См. также: Justin Kruger and David Dunning 1999: «Неверная оценка некомпетентности исходит из ошибки о себе самом, тогда как неправильная оценка высокой компетентности обусловлена ошибкой в отношении других».

Глава 13

1. DeFelipe 2002.
2. Ramón y Cajal 1937: 309.
3. Ramón y Cajal 1999 [1897]: xv—xvi; Ramуn y Cajal 1937: 278.
4. Ramón y Cajal 1937: 154.
5. Fields 2008; Giedd 2004; Spear 2013.
6. Ramón y Cajal 1999 [1897].
7. Bengtsson et al. 2005; Spear 2013.
8. Рамон-и-Кахаль, несомненно, умел хорошо продумывать свои проекты: достаточно посмотреть на сконструированную им пушку. Однако он, судя по всему, имел проблемы с видением общей картины последствий своих действий. Захваченный, например, увлекательным занятием — подрывом соседской калитки, он не мог предсказать очевидного исхода и понять, что последствия могут быть для него плачевны. См. в Shannon et al. 2011 интригующее открытие о том, что функциональная связность в неблагополучных подростках связывает дорсолатеральную премоторную зону коры головного мозга с сетью пассивного режима работы мозга («созвездие мозговых зон, связанное со спонтанной, неограниченной, самосоотносимой когнитивной деятельностью», c. 11241). По мере взросления неблагополучных подростков их поведение улучшается, названная зона коры становится связана с центрами внимания и контроля.
9. Bengtsson et al. 2005; Spear 2013. А также Thomas and Baker 2013, где отмечается (с. 226): «Результаты изучения животных заставляют предположить, что крупномасштабная организация аксонов и дендритов является стабильной и зависящая от опыта структурная пластичность взрослого мозга возникает очагами и является недолговечной». Иными словами, мы способны слегка изменить мозг, но не можем перенастроить его заново. И это разумно. См. также Дойдж, 2010 — чрезвычайно популярную книгу о пластичности мозга. Лучший технический подход к этой теме — см. в Shaw and McEachern 2001. Примечательно, что работы Рамон-и-Кахаля сейчас получают все большее признание как труды, основополагающие для нашего понимания пластичности мозга (DeFelipe 2006).
10. Ramón y Cajal 1937: 58.
11. Ibid., р. 58, 131. Способность ухватывать ключевые идеи (суть задач) оказывается более важной, чем способность дословно запомнить материал. Дословное запоминание как противоположность пониманию сути, по-видимому, кодируется иным образом. См.: Geary et al. 2008: 4–9.
12. DeFelipe 2002.
13. Ramón y Cajal 1937: 59.
14. Root-Bernstein and Root-Bernstein 1999: 88–89.
15. Bransford et al. 2000, chap. 3; Mastascusa et al. 2011, chap. 9–10.
16. Fauconnier and Turner 2002.
17. Mastascusa et al. 2011: 165.
18. Gentner and Jeziorski 1993.

Глава 14

1. Plath 1971: 34.
2. Фейнман, 2014.
3. Фейнман, 1965.
4. Этот раздел опирается на чудесную работу Prentis 1996.
5. Отрывки из песни Mandelbrot Set, © Jonathan Coulton, с любезного разрешения Джонатана Колтона. Цитата взята из текста, полностью выложенного на http://www.jonathancoulton.com/wiki/Mandelbrot_Set/Lyrics
6. Prentis 1996.
7. Cannon 1949: xiii; Ramón y Cajal 1937: 363. На схожую тему см. отличную работу DeFelipe 2010 с прекрасными иллюстрациями — изображениями, полученными на заре нейробиологических исследований.
8. Mastascusa et al. 2011: 165.
9. Keller 1984: 117.
10. См. обсуждения вопросов и ответов в Dunlosky et al. 2013.
11. http://www.youtube.com/watch?v=FrNqSLPaZLc
12. http://www.reddit.com/r/explainlikeimfive
13. См. также примечание 8 к главе 12.
14. Mastascusa et al. 2011, chap. 9–10.
15. Foerde et al. 2006; Paul 2013.

Глава 15

1. Колвин 2012; Койл 2011; Гладуэлл 2012.
2. Deslauriers et al. 2011; Felder et al. 1998; Hake 1998; Mitra et al. 2005; President’s Council of Advisors on Science and Technology 2012.
3. Ramón y Cajal 1999 [1897].
4. Kamkwamba and Mealer 2009.
5. Pert 1997: 33.
6. McCord 1978. См. обширное обсуждение этого и аналогичных исследований в Armstrong 2012. В работе Kapur and Bielaczyc 2012 указывается, что менее жесткие указания преподавателей могут привести к неожиданному улучшению качества знаний студентов.
7. Oakley et al. 2003.
8. См.: Armstrong 2012 и ссылки в этой работе.
9. Oakley 2013.

Глава 16

1. Schutz 2005. «Фред» (Fred) — предположительно анаграмма для типичных черт «расстройства восприятия общей картины в результате поражения правого полушария мозга».
2. McGilchrist 2010 дает разностороннюю информацию, подтверждающую различия между функциями полушарий, в то время как более давняя работа Efron 1990 призывает к осторожности при исследовании полушарий. См. также Nielsen et al. 2013; врач и доктор наук Джефф Андерсон, принимавший участие в исследованиях, пишет: «Совершенно верно, что некоторые функции мозга относятся либо к одному, либо к другому полушарию. Язык тяготеет к левому, внимание к правому. Однако у людей не наблюдается тенденции иметь более сильные левополушарные или правополушарные нейронные сети, все определяется отдельными связями» (University of Utah Health Care Office of Public Affairs 2013).
3. McGilchrist 2010: 192–194, 203.
4. Houdé and Tzourio-Mazoyer 2003. В работе Houdé 2002: 341 говорится: «Полученные изображения мозга показывают у людей, здоровых с точки зрения нейробиологии, прямое участие правой вентромедиальной префронтальной коры головного мозга в создании логического мышления, т.е. в том, что направляет мозг в сферу логики, где он может применять инструменты дедукции… Следовательно, правая вентромедиальная префронтальная кора может быть эмоциональным компонентом мозгового механизма, предназначенного для исправления ошибок. Точнее, эта зона может соотноситься с механизмом самоощущения, обнаруживающим условия, при которых возможны ошибки рассуждения».
5. См.: Stephen Christman et al. 2008: 403, где утверждается: «Левое полушарие поддерживает наши текущие мнения, в то время как правое оценивает и обновляет эти мнения, когда нужно. Оценка мнений, таким образом, зависит от взаимодействия между полушариями».
6. Ramachandran 1999: 136.
7. Gazzaniga 2000; Gazzaniga et al. 1996.
8. Фейнман 2011. Изначально представлено в его речи в Калифорнийском политехническом институте в 1974 г.
9. Фейнман, 2011.
10. В работе Alan Baddeley et al. 2009: 148–149 отмечается: «У нас сейчас недостаточно способов защититься от вызовов собственному самоуважению. Мы с готовностью принимаем похвалу, но скептично относимся к критике, часто считая ее плодом предубеждения критикующего. Успех мы готовы считать собственной заслугой, зато вину за неуспех мы отрицаем. Если эта уловка не срабатывает, мы успешно забываем провалы и помним успех и похвалу» (ссылка опущена).
11. Granovetter 1983; Granovetter 1973.
12. Ellis et al. 2003.
13. Beilock 2010: 34.
14. Arum and Roksa 2010: 120.

Глава 17

1. Посетите сайт доктора Фелдера: http://www4.ncsu.edu/unity/lockers/users/f/felder/public/
2. Felder 1999. Использовано с разрешения Ричарда Фелдера и Chemical Engineering Education.
3. Дополнительные материалы на эту тему см. в McClain 2011 и цитируемых там источниках.
4. Beilock 2010: 140–141.
5. Mrazek et al. 2013.
6. В работе Beilock 2010: 60 говорится: «Спортсмены в стрессовой ситуации порой пытаются контролировать свои действия так, что все их усилия оборачиваются к худшему. Такой контроль, часто называемый “паралич от анализа”, есть результат гиперактивности префронтальной зоны коры головного мозга».
7. Beilock 2010; /