Второе сокровище

У геометрии есть два великих сокровища: одно – теорема Пифагора, второе – деление отрезка в крайнем и среднем отношении. Первое мы уподобим мерке золота, второе же – драгоценному самоцвету.

Иоганн Кеплер (1571–1650)

Нет никаких сомнений, что каждый, кто воспитан в западной или ближневосточной цивилизации, во всем, что касается математики, естественных наук, философии, литературы и искусства, является учеником древних греков. Немецкий поэт Гёте писал: «Именно греки умели мечтать о жизни слаще всех народов», и это лишь скромная дань уважения отважным первопроходцам и всем открытиям, которые сделали греки в различных областях знания, ими же разработанных и названных.

Однако даже самые блестящие достижения греков во всех прочих сферах меркнут рядом с их головокружительными открытиями в математике. К примеру, всего за четыреста лет – от Фалеса Милетского (ок. 600 г. до н. э.) до «великого геометра» Аполлония Пергского (ок. 200 г. до н. э.) греки полностью сформировали основы геометрической теории.

Успехи греков в математике во многом были прямым следствием страсти к познанию ради познания, а не ради практических целей. Рассказывают, что один ученик Евклида, изучив вместе с ним некую теорему, спросил: «А что я с этого получу?» Евклид приказал рабу дать мальчику медную монету, чтобы тот увидел, что наука и в самом деле занятие прибыльное.

Образование государственного деятеля во времена Платона должно было включать в себя арифметику, геометрию, стереометрию, астрономию и музыку – и все это, как рассказывает нам пифагореец Архит, подпадало под общее название «математика». По легенде, когда Александр Великий спросил своего учителя Менехма (которому приписывают открытие эллиптической кривой, параболы и гиперболы), нельзя ли изучить геометрию как-нибудь поскорее, получил ответ: «О повелитель, в странствиях по нашему царству можно найти дороги для царей и дороги для простых граждан, однако в геометрию нет царского пути».

Платон

В таком интеллектуальном окружении и вырос Платон (428/427 г. до н. э. – 348/347 г. до н. э.), один из самых влиятельных умов Древней Греции и западной цивилизации в целом. Считается, что Платон изучал математику у пифагорейца Феодора Киренского, который первым доказал, что не только √2, но и √3, √5 и так далее вплоть до √17 – иррациональные числа. Почему он остановился на 17, никто в точности не знает, однако общего доказательства он, очевидно, вывести не сумел. Некоторые исследователи утверждают, что Феодор, вероятно, приводит самое легкое доказательство несоизмеримости, опираясь на понятие золотого сечения (идея примерно та же, что и в Приложении 2).

В своем «Государстве» Платон пишет, что математику совершенно необходимо включать в программу образования всех философов и государственных деятелей. Подобным же образом надпись над входом в его школу (Академию) гласила: «Не геометр да не войдет!» Историк математики Дэвид Юджин Смит в своей книге «Наш долг перед Грецией и Римом» (David Eugene Smith. Our Debt to Greece and Rome) называет это первым требованием к абитуриентам в истории. Восхищение математикой очевидно и тогда, когда Платон не без зависти пишет об отношении к математике в Египте, где на потеху детишкам изобрели арифметические игры, которые они изучают с удовольствием и забавы ради.

Оценивая роль Платона в развитии математики в целом и в понимании золотого сечения в частности, мы должны будем изучить не только его вклад в собственно математику, достаточно скромный, но и последствия его влияния на математические изыскания других ученых и в его собственном, и в последующих поколениях, и поддержки, которую он оказывал науке в целом. В некотором смысле Платона можно считать одним из первых чистых теоретиков. Примером его теоретических наклонностей может служить отношение к астрономии, где он предпочитал не наблюдать движение светил, а советовал «оставить небеса в покое» и сосредоточиться на более абстрактных математических небесах. Согласно Платону, настоящие звезды – это всего лишь отображение математических небес, подобно тому как геометрические чертежи – отображение абстрактных понятий точки, линии и окружности. Любопытно, что в своей выдающейся книге «История греческой математики» (Thomas Heath. A History of Greek Mathematics), изданной в 1921 году, сэр Томас Хит пишет: «Трудно разобраться, что же имел в виду Платон, когда проводил различие между видимой небесной тканью (то есть видимыми звездами, их расположением и движением), которая, безусловно, прекрасна, и подлинной небесной тканью, которым видимые небеса лишь подражают и которые бесконечно чудеснее и прекраснее».

Как астрофизик-теоретик я должен отметить, что Платон в неявном виде высказывает некоторые соображения, которым я симпатизирую. Здесь проводится различие между красотой космоса как такового и красотой теории, которая объясняет устройство Вселенной. Для наглядности приведу принцип, который открыл великий немецкий художник Альбрехт Дюрер (1471–1528).

Сложим шесть правильных пятиугольников (рис. 19) так, чтобы получился один большой пятиугольник с пятью отверстиями в форме золотых треугольников (равнобедренных треугольников с отношением стороны к основанию, равным φ). Шесть таких пятиугольников, в свою очередь, образуют еще один правильный пятиугольник, большой и более дырчатый – и так до бесконечности.

Думаю, все согласятся, что получившаяся фигура (рис. 19) удивительно красива. Однако у нее есть и обаяние другого рода – математическое: оно состоит в простоте принципа, по которому она строится. Так вот, мне кажется, это и есть математические небеса, о которых говорил Платон.

Не приходится сомневаться, что общее руководство научными изысканиями, которое осуществлял Платон в годы своего правления, гораздо важнее его непосредственного вклада в исследования. В тексте, который приписывают Филодему и относят к первому веку, мы читаем: «В те времена в математике [был достигнут] большой прогресс, и Платон им руководил и задавал задачи, которые математики ревностно решали».

Рис. 19

Тем не менее, Платон и сам очень интересовался свойствами чисел и геометрических фигур. В частности, в «Законах» он предполагает, что оптимальное число граждан в государстве – 5040, поскольку это число (а) делится на 12, 20 и 21, (б) его двенадцатая часть тоже делится на 12, (в) у него 59 делителей, в том числе все целые числа от 1 до 12, кроме 11, зато на 11 делится практически соседнее число 5038. Выбор этого числа с его свойствами позволил Платону разработать свою социально-экономическую утопию. Скажем, земля в государстве делится на 5040 наделов, а 420 из них составляют территорию каждой из двенадцати «фил». Сами жители государства делятся на четыре общественные категории – класса: свободные граждане с женами и детьми, их рабы, поселенцы-иностранцы и разнообразные заезжие гости. При выборах совета члены каждого из четырех классов избирают из своей среды по девяносто человек.

С Платоном связано и еще одно число – 216. Его он упоминает в «Государстве» в довольно-таки темном отрывке, где речь идет о том, что 216 – это шесть в кубе, а 6 – это одно из чисел, символизирующих брак (поскольку это произведение женского числа 2 и мужского числа 3). Платон и сам был учеником пифагорейцев и прекрасно знал, что сумма кубов сторон знаменитого пифагорейского треугольника – 3–4–5 – тоже равна 216.

Золотое сечение интересовало Платона, поскольку его очень занимали две темы: несоизмеримость и платоновы тела. В «Законах» Платон признается, что ему неловко, что с идеей несоизмеримости длин и с иррациональными числами он познакомился сравнительно поздно, и сокрушается, что многие греки его поколения до сих пор о них не знают.

В диалоге «Гиппий Больший» Платон признает, что подобно тому, как любое четное число может быть суммой либо двух четных, либо двух нечетных чисел, так и сумма двух иррациональных чисел может быть и иррациональной, и рациональной. Поскольку мы уже знаем, что φ – число иррациональное, рациональный отрезок прямой (то есть отрезок единичной длины), разделенный в соответствии с золотым сечением, служит примером последнего случая, хотя Платон этого, возможно, и не знал. Некоторые ученые придерживаются той точки зрения, что Платон интересовался золотым сечением как таковым. В доказательство они приводят слова Прокла Диадоха (ок. 411–485), который в «Комментарии к I книге «Начал» Евклида» пишет: «Евдокс… взяв у Платона начала сечений, разработал множество их видов» (здесь и далее пер. А. Щетникова), и полагают, что здесь говорится о том, что Платон (и Евдокс) занимались золотым сечением. Однако такое толкование вызывает серьезные сомнения со второй половины XIX века, когда многие исследователи сделали вывод, что слово «сечение», вероятно, не имеет здесь никакого отношения к золотому сечению – Прокл говорит о сечениях геометрических тел или вообще о разделении отрезков. Так или иначе, не приходится сомневаться, что основы для того, чтобы сформировать понятие о золотом сечении и вывести его определение, были заложены в годы, предшествующие открытию Платоновской Академии в 386 г. до н. э., и за время ее существования. Вероятно, ключевой фигурой и движущей силой при выведении теорем, относящихся к золотому сечению, был Теэтет (ок. 417 г. – ок. 369 г. до н. э.), который, согласно византийской энциклопедии «Суды», «первым построил пять так называемых правильных геометрических тел». Математик Папп, живший в IV веке, пишет, что Теэтет к тому же «отличал соизмеримые длины от несоизмеримых». Теэтет не принадлежал к Академии непосредственно, однако наверняка поддерживал с ней неофициальные связи.

В диалоге «Тимей» Платон берет на себя сложнейшую задачу – рассказывает о происхождении и устройстве космоса. В частности, он пытается объяснить структуру материи на примере пяти правильных многогранников, которые уже были в некоторой степени изучены пифагорейцами и подробно – Теэтетом. Пять платоновых тел (рис. 20) отличаются следующими свойствами: это единственные геометрические тела, у каждого из которых все грани – равные и равносторонние и которые можно вписать в сферу (то есть поместить все их вершины на поверхность сферы). Платоновы тела – это тетраэдр (рис. 20, а, с четырьмя гранями в виде равносторонних треугольников), куб (рис. 20, b, шесть квадратных граней), октаэдр (рис. 20, с, восемь треугольных граней), додекаэдр (рис. 20, d, двенадцать граней в виде правильных пятиугольников) и икосаэдр (рис. 20, е, двадцать треугольных граней).

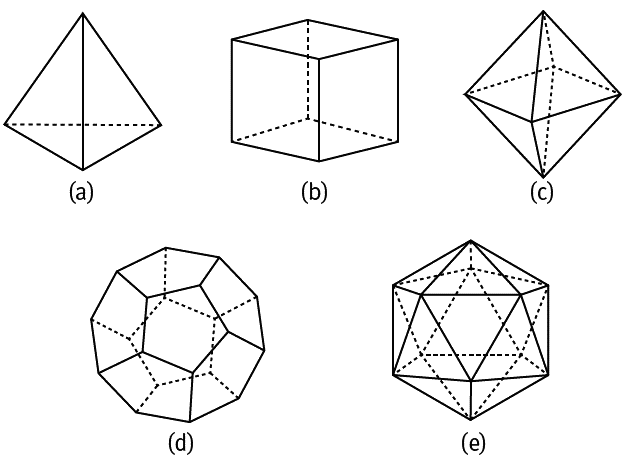
Рис. 20

Платон свел воедино идеи Эмпедокла (ок. 490–430 гг. до н. э.), согласно которому материя состоит из четырех стихий – земли, воды, огня и воздуха, – и «атомарную» теорию материи (существование невидимых частиц), которую выдвинул Демокрит из Абдеры (ок. 460 г. – ок. 370 г. до н. э.). «Единая» теория Платона предполагала, что каждой из четырех стихий соответствует своя фундаментальная частица и одно из платоновых тел. Надо понимать, что за исключением некоторых подробностей, пусть и заметных, основная идея, на которой основана теория Платона, не слишком отличается от того, как формулировал суть современной химии в XIX веке Джон Дальтон. Согласно Платону, стихия земли связана с устойчивым кубом, «всепроникающее» свойство огня – с относительно простым заостренным тетраэдром, воздух с его «подвижностью» – с октаэдром, а многоликая вода – с многогранным икосаэдром. А пятый правильный многогранник – додекаэдр – символизирует по Платону (или Тимею) Вселенную в целом или, по его словам, «его бог определил для Вселенной и прибегнул к нему в качестве образца» (пер. С. Аверинцева). Вот почему художник Сальвадор Дали решил включить в композицию своей «Тайной Вечери» парящий над столом огромный додекаэдр (см. рис. 5).

Некоторые последователи Платона никак не могли примириться с отсутствием фундаментальной стихии, которая была бы связана с додекаэдром, и кое-кто постулировал существование пятой стихии. Например, Аристотель считал, что пятая вселенская стихия (квинтэссенция) – это эфир, материал, из которого созданы небесные тела и который, по мнению Аристотеля, пронизывал всю Вселенную. Аристотель утверждал, что пятая стихия, пронизывающая всю материю, обеспечивает движение и изменение в соответствии с законами природы. Идея субстанции, пропитывающей пространство и служащей средой для распространения света, доминировала в науке вплоть до 1887 года, когда американский физик Альберт Абрахам Майкельсон и химик Эдвард Уильямс Морли провели свой знаменитый опыт и доказали, что такой среды не существует (согласно современной теории света, она и не нужна). В сущности, в ходе опыта ученые измерили скорость двух лучей света, направленных в разные стороны. Ожидалось, что поскольку Земля движется сквозь эфир, скорости двух лучей окажутся разными, однако опыт однозначно показал, что это не так. Результат опыта Майкельсона-Морли натолкнул Эйнштейна на поиски теории относительности.

Затем события приняли неожиданный поворот: в 1998 году две группы астрономов обнаружили, что наша Вселенная не просто расширяется (что уже доказал астроном Эдвин Хаббл в двадцатые годы), но расширяется с ускорением. Это открытие вызвало настоящее потрясение, поскольку астрономы, естественно, полагали, что расширение должно замедляться из-за силы тяготения. Ведь если бросить мяч вверх, стоя на поверхности Земли, его движение будет замедляться, поскольку на него действует сила тяготения, которая в конце концов и заставит его изменить направление движения на противоположное, – так и сила тяготения всей материи во Вселенной, казалось бы, должна замедлить скорость космического расширения. Открытие, что расширение не замедляется, а ускоряется, наводит на мысль о существовании какой-то «темной энергии», которая проявляется как отталкивающая сила, которая в нашей нынешней Вселенной пересиливает силу тяготения. Физики еще спорят о том, каков источник и природа этой «темной энергии». Согласно одной гипотезе эта энергия связана с квантовым полем, пронизывающим весь космос наподобие знакомого нам электромагнитного поля. Это поле очень похоже на невидимую среду Аристотеля и даже иногда называется «квинтэссенция». Кстати, в научно-фантастическом фильме Люка Бессона «Пятый элемент» «пятой стихией» – «квинтэссенцией» – была названа сила самой жизни, то, что оживляет неживое.

Теория Платона отнюдь не сводилась к символической связи фигур и стихий. Он отметил, что грани первых четырех правильных многогранников можно составить из двух видов прямоугольных треугольников: равнобедренного, с углами 45°–90°–45°, и треугольника с углами 30°–90°–60°. Далее Платон объясняет, как при помощи этих свойств можно объяснить основные «химические реакции». Например, согласно платоновой «химии», когда огонь нагревает воду, получается две частицы пара (воздуха) и одна частица огня. Формулу этой реакции можно записать так:

[вода] → 2 [воздух] + [огонь]

А если сбалансировать количество участвующих в реакции граней платоновых тел, которые соответствуют этим стихиям, то получится 20 = 2 × 8 + 4. Хотя это, конечно, никак не соответствует современному пониманию структуры материи, основная идея, что большинство фундаментальных частиц в нашей Вселенной и их взаимодействия можно описать математической теорией, которой свойственна некоторая симметрия, – краеугольный камень современных исследований в области физики частиц.

Сложные явления, которые мы наблюдаем во Вселенной, для Платона не играли существенной роли: он считал, что подлинно фундаментальна именно лежащая в их основе симметрия, а она не меняется. Это представление отнюдь не противоречит современным представлениям о законах природы. Ведь эти законы, в частности, одинаковы во всех уголках Вселенной. По этой причине законы, которые мы выводим из лабораторных экспериментов, можно применить, скажем, при изучении атома водорода и здесь, на Земле, и в галактике, лежащей в миллиардах световых лет от нас. Эта симметрия законов природы проявляется и в том, что величина, которую мы называем импульсом (равная произведению массы тела и его скорости и имеющая направление), сохраняется, то есть имеет одно и то же значение что сегодня, что через год. Подобным же образом, поскольку законы природы с течением времени не меняются, сохраняется и величина, которую мы называем энергией. Энергию невозможно получить из ничего. Вот почему современные теории, основанные на симметриях и на законах сохранения, – законы подлинно платонические.

Вероятно, интерес к многогранникам у пифагорейцев был первоначально вызван наблюдениями над кристаллами пирита в Южной Италии, где находилась пифагорейская школа. Кристаллы пирита, он же серный колчедан, часто имеют в форму додекаэдра. Однако платоновы тела, их красота и математические свойства поражали воображение ученых и спустя много столетий после Платона – и упоминания о них мы встречаем в самых неожиданных местах. Например, в научно-фантастическом романе Сирано де Бержерака (1619–1655) «Иной мир» автор строит летательный аппарат в виде икосаэдра, чтобы сбежать из башни, где он заточен, и приземлиться на Солнце.

Золотое сечение, число φ, играет важнейшую роль в пропорциях и симметрических свойствах некоторых платоновых тел. В частности, додекаэдр с длиной ребра (места, где сходятся две грани) в одну единицу, имеет площадь поверхности в 15 × φ / (√3 – φ) и объем 5 × φ³ / (6–2 × φ). Подобным же образом икосаэдр с длиной ребра в одну единицу имеет объем (5 × φ⁵)/6.

Из симметрии платоновых тел можно вывести интересные следствия. Например, у куба и октаэдра одинаковое число ребер – 12, – однако число граней и вершин взаимно обратное – у куба шесть граней и восемь вершин, а у октаэдра восемь граней и шесть вершин. То же самое можно сказать о додекаэдре и икосаэдре – у обоих по 30 ребер, но у додекаэдра 12 граней и 20 вершин, а у икосаэдра – наоборот. Это симметрическое сходство платоновых тел позволяет очень интересно вписывать правильный многогранник в его «двойник». Если соединить центры граней куба, получится октаэдр (рис. 21), а если соединить центры граней октаэдра, получится куб. Ту же самую процедуру можно проделать, чтобы вписать икосаэдр в додекаэдр и наоборот – а соотношение длин ребер каждого многогранника (одного в другом) опять же можно выразить при помощи золотого сечения: это φ²/√5. А тетраэдр – сам себе «двойник»: если соединить четыре центра граней тетраэдра, получится другой тетраэдр.

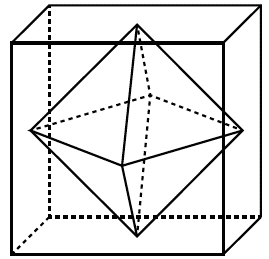
Рис. 21

Хотя в античности были известны не все свойства платоновых тел, ни от Платона, ни от его последователей не скрылась их красота. В некотором смысле даже трудности при построении этих фигур, которые поначалу возникали (пока не были выведены методы, связанные с золотым сечением), можно считать их имманентными свойствами. Ведь последние слова диалога «Гиппий Больший» гласят: «Прекрасное – трудно». Греческий историк Плутарх (ок. 46 – ок. 120) в своем сочинении «Об упадке оракулов» пишет: «Пирамида [тетраэдр], октаэдр, икосаэдр, додекаэдр, все первоначальные фигуры, которые предсказывает Платон, прекрасны благодаря симметрии и равенствам в их отношениях, и ничего лучше и даже ничего сопоставимого с ними Природа не создала».

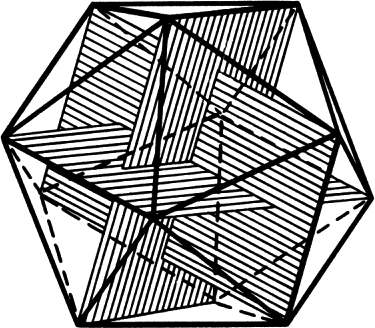
Рис. 22

Как уже упоминалось, икосаэдр и додекаэдр тесно связаны с золотым сечением, и связей этих несколько. Например, 12 вершин икосаэдра можно объединить в три группы по четыре, и вершины из каждой группы будут лежать на углах золотого прямоугольника, то есть прямоугольника, у которого длины сторон соотносятся как φ. Прямоугольники перпендикулярны друг другу, а единственная их общая точка лежит в геометрическом центре икосаэдра (рис. 22). Подобным же образом центры 12 пятиугольных граней додекаэдра можно объединить в три группы по четыре, и каждая из этих групп также составит золотой прямоугольник. Тесные связи между некоторыми плоскими фигурами, скажем, правильным пятиугольником и пентаграммой, и золотым сечением привели к неизбежному выводу, что интерес греков к золотому сечению начался, вероятно, с попыток построить подобные плоские фигуры и геометрические тела. Подобные математические изыскания велись примерно в начале IV века до н. э. Однако до нас дошли и многочисленные утверждения, что на основе золотого сечения создан и архитектурный проект Парфенона, который был построен и украшен в 447–432 годах до н. э., в правление Перикла. Насколько обоснованны подобные заявления?