Невоспетый герой Возрождения?

Лука Пачоли родился в 1445 году в том же тосканском городке Борго Сансеполькро, где родился и держал мастерскую Пьеро делла Франческа. Более того, начальное образование Лука получил именно в мастерской Пьеро. Однако, в отличие от других учеников, выказывавшим способности к живописи – некоторым из них, например, Пьетро Перуджино, суждено было стать великими живописцами, – Лука оказался более склонным к математике. Пьеро и Пачоли сохраняли дружеские отношения и в дальнейшем: доказательством тому служит то, что Пьеро изобразил Пачоли в виде Св. Петра Веронского (Петра Мученика) на «Алтаре Монтефельтро». Еще сравнительно молодым человеком Пачоли перебрался в Венецию и стал там наставником трех сыновей состоятельного торговца. В Венеции он продолжил математическое образование под руководством математика Доменико Брагадино и написал первую книгу по арифметике.

В 1470 годах Пачоли изучал теологию и постригся в монахи-францисканцы. С тех пор его стало принято называть фра Лука Пачоли. В последующие годы он много путешествовал, преподавал математику в университетах в Перудже, Задаре, Неаполе и Риме. В то время Пачоли, вероятно, некоторое время учил и Гвидобальдо Монтефельтро, которому в 1482 году предстояло стать герцогом Урбинским. Лучший, пожалуй, портрет математика – это картина кисти Якопо де Барбари (1440–1515), изображающая, как Лука Пачоли дает урок геометрии (рис. 50, картина находится в музее Каподимонте в Неаполе). Справа на книге Пачоли «Summa» покоится одно из платоновых тел – додекаэдр. Сам Пачоли во францисканской рясе (тоже похожий на правильный многогранник, если приглядеться) копирует чертеж из XIII книги «Начал» Евклида. Прозрачный многогранник под названием ромбокубоктаэдр (одно из архимедовых тел, многогранник с 26 гранями, 18 из которых – квадраты, а 8 – равносторонние треугольники), висящий в воздухе и наполовину наполненный водой, символизирует чистоту и вечность математики. Художнику удалось с поразительным искусством передать преломление и отражение света в стеклянном многограннике. Личность ученика Пачоли, изображенного на этой картине, стала предметом споров. В частности, предполагают, что этот юноша – сам герцог Гвидобальдо. Английский математик Ник Маккиннон в 1993 году выдвинул интересную гипотезу. В своей статье «Портрет фра Лука Пачоли», опубликованной в «Mathematical Gazette» и основанной на весьма солидных исследованиях, Маккиннон делает вывод, что это портрет великого немецкого живописца Альбрехта Дюрера, которого очень интересовали и геометрия, и перспектива (а к его отношениям с Пачоли мы еще вернемся чуть ниже). И в самом деле, лицо ученика поразительно похоже на автопортрет Дюрера.

Рис. 50

В 1489 году Пачоли вернулся в Борго Сансеполькро, получив некоторые привилегии от самого Папы, однако местный религиозный истеблишмент встретил его с ревнивой недоброжелательностью. Около двух лет ему даже запрещали преподавать. В 1494 году Пачоли отправился в Венецию печатать свою книгу «Summa», которую посвятил герцогу Гвидобальдо. «Summa» по природе и по размаху (около 600 страниц) – подлинно энциклопедический труд, где Пачоли свел воедино все, что было на то время известно в области арифметики, алгебры, геометрии и тригонометрии. В своей книге Пачоли не стесняется заимствовать задачи об икосаэдре и додекаэдре из «Трактата» Пьеро делла Франческа и другие задачи по геометрии, а также по алгебре, из трудов Фибоначчи и других ученых (правда, обычно выражает благодарность автору, как полагается). Пачоли признается, что его главный источник – это Фибоначчи, и говорит, что там, где нет ссылок на кого-то другого, труды принадлежат Леонардо Пизанскому. Интересный раздел «Summa» – бухгалтерская система двойной записи, метод, позволяющий прослеживать, откуда деньги пришли и куда ушли. Эту систему изобрел не сам Пачоли, он лишь свел воедино приемы венецианских купцов эпохи Возрождения, однако считается, что это первая книга по бухгалтерии в истории человечества. Так и получилось, что желание Пачоли «позволить дельцу незамедлительно получать сведения о своих активах и денежных обязательствах» стяжало ему прозвище «Отец бухгалтерии», и в 1994 году бухгалтеры всего мира отмечали пятисотлетие «Summa» в Сансеполькро, как теперь называется этот город.

В 1480 году место герцога Миланского фактически занял Людовико Сфорца. На самом деле он был всего лишь регентом при настоящем герцоге, которому тогда было только семь лет; это событие положило конец периоду политических интриг и убийств. Людовико решил украсить свой двор художниками и учеными и в 1482 году пригласил Леонардо да Винчи в «коллегию герцогских инженеров». Леонардо очень интересовался геометрией, в особенности – ее практическим приложением в механике. По его словам, «Механика – это рай среди математических наук, поскольку именно она порождает плоды математики». А впоследствии, в 1496 году, именно Леонардо, скорее всего, добился, чтобы герцог пригласил ко двору и Пачоли в качестве учителя математики. Леонардо, несомненно, учился геометрии и у Пачоли, а ему привил любовь к живописи.

Во время пребывания в Милане Пачоли завершил работу над трехтомным трактатом «О божественной пропорции», вышедшим в свет в Венеции в 1509 году. Первый том, «Compendio de Divina Proportione» («Компендиум о божественной пропорции»), содержит подробный свод всех качеств золотого сечения (его Пачоли называет «божественной пропорцией) и исследование платоновых тел и других многогранников. На первой странице «О божественной пропорции» Пачоли несколько выспренно заявляет, что это «труд, необходимый всем пытливым, ясным человеческим умам, в котором всякий, кто любит изучать философию, перспективу, живопись, ваяние, зодчество, музыку и иные математические дисциплины, найдет весьма тонкое, изящное и прелестное учение и получит наслаждение от разнообразных вопросов, затрагивающих все тайные науки».

Первый том трактата «О божественной пропорции» Пачоли посвятил Людовико Сфорца, а в пятой главе он перечисляет пять причин, почему, по его мнению, золотое сечение следует именовать не иначе как божественной пропорцией.

1. «Она одна, едина и всеобъемлюща». Пачоли сравнивает уникальность золотого сечения с тем обстоятельством, что «Единый» – «Высочайший эпитет самого Господа».

2. Пачоли видит сходство между тем, что определение золотого сечения включает в себя ровно три длины (АС, СВ и АВ на рис. 24), и существованием Святой Троицы – Отца, Сына и Святого Духа.

3. Для Пачоли непостижимость Бога и то обстоятельство, что золотое сечение – иррациональное число, эквивалентны. Вот как он пишет: «Подобно тому, как Господа нельзя определить должным образом и невозможно постичь его посредством слов, так и наша пропорция не может быть передана постижимыми цифрами и выражена через какое бы то ни было рациональное количество, она навеки останется тайной, сокрытой от всех, и математики именуют ее иррациональной».

4. Пачоли сравнивает вездесущесть и неизменность Бога с самоподобием, которое связывают с золотым сечением: его значение всегда неизменно и не зависит от длины отрезка, который делят в соответствующей пропорции, или с размером правильного пятиугольника, в котором вычисляют соотношения длин.

5. Пятая причина показывает, что Пачоли придерживался даже более платоновских взглядов на бытие, чем сам Платон. Пачоли утверждает, что подобно тому, как Господь дал жизнь мирозданию посредством квинтэссенции, нашедшей отражение в додекаэдре, так и золотое сечение дало жизнь додекаэдру, поскольку невозможно построить додекаэдр без золотого сечения. Пачоли добавляет, что невозможно сравнить остальные платоновы тела (символы воды, земли, огня и воздуха) друг с другом без опоры на золотое сечение.

В самой книге Пачоли постоянно разглагольствует о качествах золотого сечения. Он последовательно анализирует 13 так называемых «эффектов» «божественной пропорции» и каждому из этих «эффектов» приписывает эпитеты вроде «неотъемлемый», «неповторимый», «чудесный», «высочайший» и т. д. Например, тот «эффект», что золотые прямоугольники можно вписать в икосаэдр (рис. 22), он называет «непостижимым». Он останавливается на 13 «эффектах», сделав вывод, что «следует завершить этот перечень ради спасения души», поскольку именно 13 человек сидели за столом во время Тайной Вечери.

Не приходится сомневаться, что Пачоли очень интересовался живописью, и целью создания трактата «О божественной пропорции» отчасти было отточить математическую основу изящных искусств. На первой же странице книги Пачоли выражает желание посредством золотого сечения открыть художникам «тайну» гармонических форм. Чтобы обеспечить привлекательность своего труда, Пачоли заручился услугами лучшего иллюстратора, о каком только мог мечтать любой писатель: сам Леонардо да Винчи снабдил книгу 60 рисунками многогранников как в виде «скелетов» (рис. 51), так и в виде сплошных тел (рис. 52). За благодарностью дело не встало – Пачоли написал о Леонардо и его вкладе в книгу так: «Лучший живописец и мастер перспективы, лучший зодчий, музыкант, человек, наделенный всеми возможными достоинствами – Леонардо да Винчи, который придумал и исполнил цикл схематических изображений правильных геометрических тел». Сам же текст, признаться, не достигает заявленных высоких целей. Хотя начинается книга с сенсационных тирад, далее следует довольно-таки обычный набор математических формул, небрежно разбавленных философскими определениями.

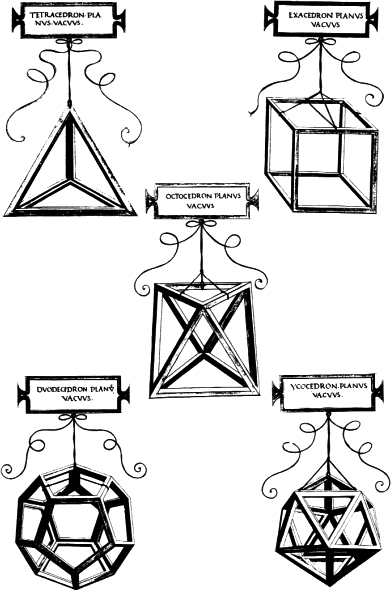
Рис. 51

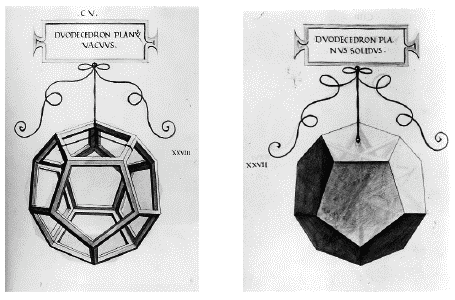
Рис. 52

Вторая книга трактата «О божественной пропорции» посвящена влиянию золотого сечения на архитектуру и его проявлениям в структуре человеческого организма. В основном трактат Пачоли основан на работе римского архитектора Марка Витрувия Поллиона (ок. 70–25 гг. до н. э.). Витрувий писал:

Центральная точка человеческого тела – это, естественно, пупок. Ведь если человек ляжет ничком на спину и раскинет руки и ноги, а на пупок ему поставить циркуль, то пальцы рук и ног у него коснутся описанной окружности. И подобно тому, как тело человека вписывается в круг, так можно из него получить и квадрат. Ведь если мы измерим расстояние от подошв до макушки, а затем применим эту меру к раскинутым рукам, то окажется, что ширина фигуры в точности равна высоте, как и в случае плоских поверхностей, имеющих форму идеального квадрата.

Ученые Возрождения считали этот отрывок очередным доказательством связи между природной и геометрической основой красоты, и это привело к созданию концепции витрувианского человека, которого так прекрасно изобразил Леонардо (рис. 53, в настоящее время рисунок хранится в Галерее Академии в Венеции). Подобным же образом книга Пачоли начинается с обсуждения пропорций человеческого тела, «поскольку в теле человека можно найти пропорции любых видов, по воле Всевышнего явленные через сокровенные тайны природы».

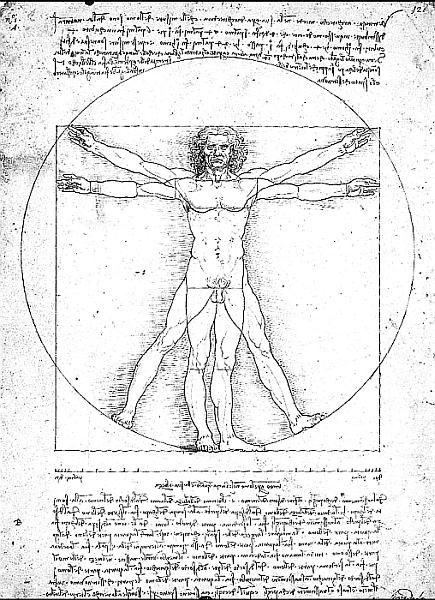
Рис. 53

В литературе можно часто встретить утверждения, что Пачоли будто бы считал, что золотое сечение определяет пропорции всех произведений искусства, однако на самом деле все совсем не так. Говоря о пропорции и внешнем устройстве, Пачоли в основном ссылается на витрувианскую систему, основанную на простых (рациональных) дробях. Писатель Роджер Герц-Фишлер проследил, откуда взялось распространенное заблуждение, что золотое сечение будто бы служило для Пачоли каноном пропорций: оно восходит к ложному утверждению, сделанному в издании «Истории математики» французских математиков Жана Этьена Монтюкла и Жерома де Лаланда 1799 года (Jean Etienne Montucla, Jérôme de Lalande. Histoire de Mathématiques).

Третий том трактата «О божественной пропорции» (короткая книга в трех частях о пяти правильных геометрических телах), в сущности, представляет собой дословный перевод на итальянский «Пяти правильных многогранников» Пьеро делла Франческа, написанных на латыни. То, что Пачоли ни разу не упоминает, что он всего лишь переводчик книги, вызвало у историка искусств Джорджо Вазари горячее осуждение. Вазари пишет о Пьеро делла Франческа:

Почитаясь редкостным мастером в преодолении трудностей правильных тел, а также арифметики и геометрии, он, пораженный в старости телесной слепотой, а затем и смертью, не успел выпустить в свет доблестные труды свои и многочисленные книги, им написанные, кои и поныне хранятся в Борго, у него на родине. Тот, кто должен был всеми силами стараться приумножить его славу и известность, ибо у него научился всему, что знал, пытался как злодей и нечестивец изничтожить имя Пьеро, своего наставника, и завладеть для себя почестями, которые должны были принадлежать одному Пьеро, выпустив под своим собственным именем, а именно брата Луки из Борго [Пачоли], все труды этого почтенного старца, который помимо вышеназванных наук был превосходным живописцем. (Пер. М. Глобачева)

Так можно ли считать Пачоли плагиатором? Весьма вероятно, хотя в «Summa» он все же воздает Пьеро должное, называя его «монархом в живописи наших времен» и человеком, который «знаком читателю по многочисленным трудам по искусству живописи и силе линии в перспективе».

Р. Эмметт Тейлор (1889–1956) в 1942 году выпустил книгу под названием «Нет царского пути. Лука Пачоли и его время» (R. Emmett Taylor. No Royal Road: Luca Pacioli and His Times). В этой книге Тейлор относится к Пачоли с большой симпатией и отстаивает ту точку зрения, что, если исходить из стиля, Пачоли, вероятно, не имеет никакого отношения к третьему тому трактата «О божественной пропорции», и это сочинение ему лишь приписывают.

Так это или не так, неизвестно, однако несомненно, что если бы не печатные труды Пачоли, идеи и математические конструкции Пьеро, которые не были опубликованы в печатном виде, вероятно, не стяжали бы той известности, которая им в результате досталась. Более того, до времен Пачоли золотое сечение было известно под устрашающими названиями вроде «крайнее и среднее отношение» или «пропорция, имеющая среднее и два экстремума», и само это понятие было известно одним лишь математикам.

Публикация «О божественной пропорции» в 1509 году вызвала новую вспышку интереса к теме золотого сечения. Теперь концепцию рассматривали, что называется, свежим взглядом: раз о ней издали книгу, значит, она достойна уважения. Само название золотого сечения оказалось наделено теолого-философским смыслом (божественная пропорция), а это также делало золотое сечение не просто математическим вопросом, а темой, в которую могли углубиться интеллектуалы самого разного толка, причем это разнообразие со временем лишь ширилось. Наконец, с появлением труда Пачоли золотое сечение стали изучать и художники, поскольку теперь о нем говорилось не только в откровенно математических трактатах – Пачоли рассказал о нем так, что этим понятием можно было пользоваться.

Рисунки Леонардо к трактату «О божественной пропорции», начертанные (по выражению Пачоли) «его неописуемой левой рукой», также оказали определенное воздействие на читательскую аудиторию. Вероятно, это были первые изображения многогранников в схематическом, скелетоподобном виде, что позволяло легко представить их себе со всех сторон. Возможно, Леонардо рисовал многогранники с деревянных моделей, поскольку в документах Совета Флоренции сохранились записи о том, что город приобрел набор деревянных моделей Пачоли, дабы выставить их на всеобщее обозрение. Леонардо рисовал не только схемы для книги Пачоли, наброски всевозможных многогранников мы видим повсюду в его заметках. В одном месте Леонардо дает приблизительный метод построения правильного пятиугольника. Слияние математики с изобразительным искусством достигает пика в «Trattato della pittura» («Трактате о живописи»), который составил Франческо Мельци, унаследовавший рукописи Леонардо, по его записям. Начинается трактат с предупреждения: «Тот, кто не математик, да не прочтет мои труды!» – едва ли такое заявление найдешь в современных учебниках по изобразительному искусству!

Рисунки геометрических тел из трактата «О божественной пропорции» вдохновили и фра Джованни да Верона на создание работ в технике интарсии. Интарсия – это особый вид инкрустации деревом по дереву, создание сложных плоских мозаик. Около 1520 года фра Джованни создал инкрустированные панели с изображением икосаэдра, причем в качестве образца он почти наверняка пользовался схематическими рисунками Леонардо.

Пути Леонардо и Пачоли несколько раз пересекались и после завершения трактата «О божественной пропорции». В октябре 1499 года оба бежали из Милана, когда его захватила французская армия короля Людовика XII. Потом ненадолго останавливались в Мантуе и в Венеции и на некоторое время осели во Флоренции. За тот период, когда они дружили, Пачоли создал еще два труда по математике, прославивших его имя – перевод на латынь «Начал» Евклида и книгу о математических развлечениях, оставшуюся неопубликованной. Перевод «Начал», который выполнил Пачоли, был аннотированной версией, основанной на более раннем переводе Джованни Кампано (1220–1296), который был напечатан в Венеции в 1482 году (это было первое печатное издание). Добиться публикации сборника занимательных задач по математике и поговорок «De Viribus Quantitatis» («О способностях чисел») Пачоли при жизни так и не смог – он скончался в 1517 году. Эта работа была плодом сотрудничества между Пачоли и Леонардо, и в заметках самого Леонардо содержится довольно много задач из трактата «De Viribus Quantitatis».

Конечно, прославила фра Луку Пачоли отнюдь не оригинальность научной мысли, а его влияние на развитие математики в целом и на историю золотого сечения в частности, и этих его заслуг отрицать никак нельзя.