Измененная, вновь воскресаю прежней

В истории математика не было семейства, породившего столько знаменитых математиков, сколько семья Бернулли: целых тринадцать!

Испугавшись «Испанской ярости» – кровопролитного восстания, поднятого в Нидерландах испанскими солдатами, – семейство бежало из Нидерландов, находившихся под властью испанских католиков, в Швейцарию, в город Базель. Три члена семьи, братья Якоб (1654–1705) и Иоганн (1667–1748) и второй сын Иоганна Даниил (1700–1782), были в интеллектуальном отношении на голову выше остальных родственников. Как ни странно, ожесточенные семейные распри прославили Бернулли чуть ли не в той же степени, что и многочисленные достижения в математике. Однажды Якоб с Иоганном повздорили особенно сильно. Началась ссора из-за разногласий по поводу решения знаменитой задачи по механике. Эта задача известна под названием «брахистохрона» (от греческих слов «брахистос», «кратчайший», и «хронос», «время») и состоит в том, чтобы найти кривую, по которой частица попадет из точки А в точку В под воздействием одной лишь силы гравитации за кратчайшее время. Братья независимо пришли к одному и тому же решению, однако в выкладках Якоба была ошибка, и он впоследствии пытался выдать выкладки Иоганна за свои. Печальным последствием этих событий стало то, что Иоганн стал профессором в Гронингене и до самой смерти брата ни разу не наведывался в Базель.

Связь Якоба Бернулли с золотым сечением прослеживается благодаря другой знаменитой кривой. Якоб написал трактат под названием «Spira Mirabilis» («Чудесная спираль») и посвятил ее особой разновидности спирали. Красота так называемой логарифмической спирали (рис. 37, названием она обязана тому, как радиус кривой возрастает по мере движения по часовой стрелке) настолько заворожила Якоба, что он завещал начертать эту фигуру и девиз, который он ей приписал – «Eadem mutate resurgo», «Измененная, вновь воскресаю прежней» – на своем надгробии.

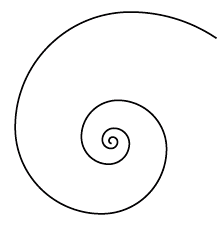
Рис. 37

Девиз отражает фундаментальное уникальное качество логарифмической кривой: с увеличением размера она не меняет формы. Эта черта называется самоподобием. Очарованный этим качеством, Якоб писал, что логарифмическую спираль «можно сделать символом как стойкости и постоянства в трудных обстоятельствах, так и человеческого организма, который после всех перемен, даже после смерти, восстанавливает точное свое подобие и полное совершенство».

Если немного подумать, станет ясно, что именно это свойство требуется для многих явлений роста и развития в природе. Например, по мере того как моллюск наутилус помпилиус (рис. 4) растет в своей раковине, он создает камеры все просторнее и просторнее, а те, которые стали ему малы, запечатывает. Каждая прибавка в длине раковины влечет за собой и пропорциональное увеличение радиуса, поэтому общая форма раковины остается неизменной. То есть «домик» у наутилуса всю жизнь одинаковый, и моллюску не приходится потом, например, сдвигать центр тяжести раковины. То же свойство присуще и бараньим рогам – они тоже имеют форму логарифмической спирали, хотя и не лежат в одной плоскости, – и изгибу слоновьих бивней. Логарифмическая спираль, набирая размер, становится шире, расстояние между «витками» увеличивается по мере отдаления от центра – так называемого полюса. Причем поворот на равные углы увеличивает расстояние от полюса на равные промежутки. Если бы мы, вооружившись микроскопом, увеличили бы витки, невидимые невооруженным глазом, до таких размеров, как на рис. 37, они в точности совпали бы с большой спиралью. Это свойство и отличает логарифмическую спираль от другой известной кривой, так называемой архимедовой спирали (в честь великого греческого математика Архимеда (ок. 287–212 гг. до н. э.), который подробно описал ее в своем трактате «О спиралях»). Архимедову спираль мы наблюдаем на торце рулонов туалетной бумаги или в рисунке каната, свернутого на полу. У спирали этого типа расстояние между витками всегда постоянно. К сожалению, каменщик, изготавливавший надгробие Якоба Бернулли, изобразил на нем по ошибке скорее архимедову, чем логарифмическую спираль, что, конечно, наверняка очень огорчило бы ученого.

Природа обожает логарифмические спирали. Похоже, это ее любимый узор – она украшает им все подряд, от подсолнухов и ракушек до водоворотов, смерчей и гигантских спиральных галактик. Постоянная форма логарифмической спирали любого размера прекрасно проявляется в природе и в очертаниях раковин микроскопических одноклеточных организмов под названием фораминиферы. Хотя спиральные ракушки в данном случае – структуры сложные, это не просто трубочка, рентгеновские изображения внутренней структуры ископаемых раковин этих существ показывают, что за много миллионов лет их рисунок – логарифмическая спираль – остался прежним. В своем классическом труде «Изгибы жизни» (Theodore Andrea Cook. The Curves of Life, 1914) английский писатель и издатель Теодор Андреа Кук приводит массу примеров появления спиралей, не только логарифмических, как в природе, так и в искусстве. Он пишет о спиралях в самых разных предметах – это и вьющиеся растения, и человеческий организм, и винтовые лестницы, и татуировки маори. Когда Кук объясняет, что подвигло его на создание книги, то пишет: «…Существованию этих глав о спиральных структурах нет никаких оправданий, кроме увлекательности и красоты самих исследований». Скажем, в этюде к мифологическому сюжету «Леда и лебедь» Леонардо да Винчи косы Леды почти точно повторяют форму логарифмической спирали (рис. 38). Леонардо много раз повторял этот мотив в этюдах спиралей в облаках и в воде – этому посвящен потрясающий цикл рисунков «Потоп». В этом произведении Леонардо сочетал научные исследования над катастрофическими наводнениями с аллегорическими аспектами разрушительных сил, грянувших с небес. Вот как Леонардо описывает бурный поток: «Внезапно нахлынувшие воды обрушиваются в омут, который их вмещает, сметая разнообразные препятствия своими бурными завихрениями… Натиск водоворота, возникающего в месте низвержения воды, швыряет воду прямо на другие водовороты, закрученные в противоположном направлении».

Художник Эдвард Б. Эдвардс, живший в ХХ веке, разработал на основе логарифмической спирали сотни декоративных мотивов – многие из них приведены в его книге «Дизайн и орнаменты с динамической симметрией» (Edward B. Edwards. Pattern and Design with Dynamic Symmetry), например, узоры, показанные на рис. 39.

Рис. 38

Рис. 39

Логарифмическая спираль и золотое сечение неотделимы друг от друга. Рассмотрим серию сложенных воедино золотых прямоугольников, которые получились у нас, когда мы отрезали квадраты от золотых прямоугольников побольше (рис. 40; об этом мы уже немного говорили в главе 4). Если последовательно соединить точки, в которых эти «вертящиеся квадраты» делят стороны в золотом сечении, у нас получится логарифмическая спираль, сворачивающаяся внутрь, к полюсу (то есть в точку на пересечении диагоналей на рис. 25, которой дали пышное название «Око Господне».

Логарифмическую спираль можно получить и из золотого треугольника. В главе 4 мы видели, что если начать с золотого треугольника (напомню, что это равнобедренный треугольник, в котором сторона относится к основанию в золотом сечении) и разделим биссектрисой угол при основании, у нас получится золотой треугольник поменьше. Если и дальше делить биссектрисами углы при основании треугольника – до бесконечности – получится водоворот из треугольников. Если соединить их вершины, получится логарифмическая спираль (рис. 41).

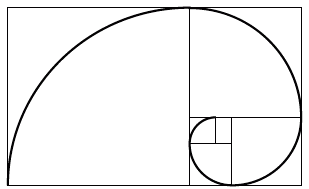
Рис. 40

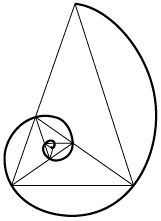
Рис. 41

Еще логарифмическую спираль называют равноугольной спиралью. Этот термин ввел в 1638 году французский математик и философ Рене Декарт (1596–1650), по имени которого названы числа, определяющие положение точки на плоскости относительно двух осей – декартова система координат.

Слово «равноугольная» отражает другое уникальное качество логарифмической спирали. Если прочертить прямую линию из полюса к любой точке спирали, она пересечет кривую под одним и тем же углом (рис. 42). Этим качеством пользуются соколы, когда бросаются на добычу. Соколы-сапсаны – одни из самых быстрых птиц на земле, когда они пикируют к цели, то разгоняются до двухсот километров в час. Однако они могли бы летать даже быстрее, если бы приближались к добыче по прямой, а не по спиральной траектории. Биолог Ванс Э. Такер из Университета Дюка в Северной Каролине многие годы интересовался, почему же сапсаны не выбирают кратчайший путь к добыче. Затем он понял, что поскольку глаза у соколов расположены по сторонам головы, то чтобы воспользоваться преимуществом, которое дает этим птицам острейшее зрение, им приходится поворачивать голову на 40 градусов в ту или иную сторону. В ходе экспериментов в аэродинамической трубе Такер выяснил, что такой поворот головы заметно тормозит движение сокола. Результаты этих исследований были опубликованы в ноябрьском выпуске «Journal of Experimental Biology» за 2000 год и показывают, что соколы держат голову прямо и летят по логарифмической спирали. А поскольку спираль обладает свойством равноугольности, такая траектория позволяет птице, разгоняясь до предельных скоростей, не упускать добычу из виду.

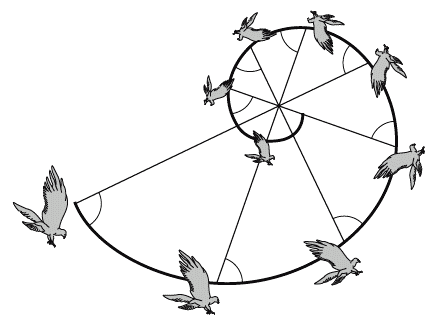
Рис. 42

Как ни удивительно, та же самая спиральная кривая, какую мы наблюдаем у ракушек одноклеточных фораминифер и в сердцевине подсолнуха, та же, которая направляет полет сокола, обнаруживается и в «звездных системах, группирующихся в одной плоскости, наподобие Млечного пути», о которых философ Иммануил Кант (1724–1804) размышлял задолго до того, как их удалось пронаблюдать (рис. 43). Эти системы было принято называть «островные Вселенные» – гигантские галактики, в которых таких звезд, как наше Солнце, сотни миллиардов. Наблюдения на орбитальном телескопе им. Э. Хаббла показали, что в наблюдаемой Вселенной примерно сто миллиардов галактик, многие из них спиральные. Трудно придумать более удачную иллюстрацию к величественному видению английского поэта, художника и мистика Уильяма Блейка (1757–1827), писавшего:

 

В одном мгновенье видеть вечность,

Огромный мир – в зерне песка,

В единой горсти – бесконечность

И небо – в чашечке цветка.

 

(Пер. С. Маршака)

Почему же галактики так часто имеют форму спирали? Спиральные галактики вроде нашего Млечного пути – это относительно плоский диск, вроде блина, состоящий из газа, звездной пыли и звезд. Весь галактический диск вращается вокруг центра галактики. Например, по соседству от Солнца орбитальная скорость вокруг центра Млечного пути составляет примерно 225 километров в секунду, а на полный оборот понадобится около 225 миллионов лет. На других расстояниях от центра и скорость иная – чем ближе к центру, тем больше, а на дальних дистанциях меньше, то есть галактический диск вращается не как твердый диск, а дифференциально. Если посмотреть на диск сверху, у спиральных галактик видны спиральные рукава, которые начинаются вблизи от центра и расходятся в разные стороны по большей части диска, как на рис. 43, где изображена галактика Водоворот. Спиральные рукава – это те области галактического диска, где рождается много новых звезд.

Рис. 43

Поскольку новые звезды самые яркие, спиральную структуру других галактик нам видно издалека. Главный вопрос, на который надо было ответить астрофизикам, состоял вот в чем: как спиральным рукавам удается так долго сохранять форму? Ведь внутренние части диска вращаются быстрее внешних, так что любой крупномасштабный узор, так или иначе связанный с материалом диска, то есть со звездами, долго бы не удержался. Спиральная структура, привязанная к одному и тому же скоплению звезд и облаков газа, неизбежно нарушилась бы, а наблюдениями это не подтверждается. Долголетие спиральных рукавов объясняется волнами плотности – волнами сжатия газа, проходящими по галактическому диску, – которые по пути сжимают газовые облака и способствуют зарождению новых звезд. Спиральный узор, который мы наблюдаем, это попросту проявление тех областей диска, где плотность выше средней и много новых звезд. Поэтому узор постоянно воссоздается и не нарушается. Подобное же положение дел мы наблюдаем поблизости от огороженного участка дорожных работ на крупном шоссе. Плотность машин поблизости от закрытого участка выше, потому что водители вынуждены там притормаживать. Если сделать фотографию шоссе с птичьего полета с большой выдержкой, можно зафиксировать плотность пробки поблизости от места ремонта. Волна плотности машин не связана с каким-то конкретным набором автомобилей, точно так же и спиральный узор не связан с тем или иным «куском» материала диска. Еще одна общая черта – тот факт, что волна плотности движется через диск медленнее движения самих звезд и газа, точно так же как скорость, с которой участок дорожных работ перемещается вдоль шоссе, как правило, гораздо медленнее, чем двигаются отдельные автомобили, которым ничто не мешает.

Движущая сила, которая отражает движение звезд и газовых облаков и порождает спиральную волну плотности (аналогично тому, как дорожные работы ограничивают движение автомобилей, оставляя им меньше полос) – это сила тяготения, вызванная тем обстоятельством, что распределение материи в галактике не полностью симметрично. Например, набор эллиптических орбит вокруг центра галактики (рис. 44, а), в котором каждая орбита несколько возмущена (повернута), причем сила возмущения меняется в зависимости от расстояния от центра, приводит к возникновению спирального узора (рис. 44, b).

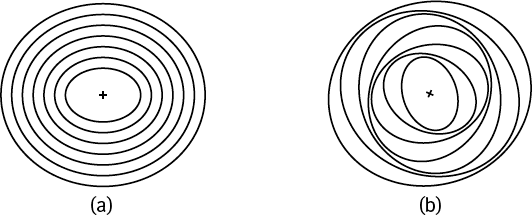
Рис. 44

В сущности, надо радоваться, что сила тяготения ведет себя в нашей Вселенной именно так, а не иначе. Согласно закону всемирного тяготения Ньютона, всякая масса притягивает всякую другую массу и сила притяжения уменьшается с расстоянием. В частности, увеличение расстояния вдвое ослабляет силу тяготения в четыре раза (сила тяготения обратно пропорциональна квадрату расстояния). Ньютоновы законы движения показывают, что в результате зависимости силы тяготения от расстояния орбиты планет вокруг Солнца имеют форму эллипсов. А теперь представьте себе, что было бы, живи мы во Вселенной, где гравитация ослабевает при удвоении расстояния с коэффициентом восемь, а не четыре – то есть если бы сила тяжести уменьшалась в зависимости от куба расстояния. В такой Вселенной законы Ньютона предсказывали бы одну-единственную возможную орбиту для планеты – логарифмическую спираль. Иначе говоря, Земля либо по спирали устремилась бы к Солнцу, либо умчалась бы в космос.

Леонардо Фибоначчи, благодаря которому в Европе и началась кипучая математическая деятельность, в наши дни отнюдь не забыт. В сегодняшней Пизе, в садах Скотто на территории Новой крепости работы Сангалло стоит памятник Фибоначчи, воздвигнутый в XIX веке, а неподалеку проходит улица, названная в его честь – она идет вдоль южного берега реки Арно. Начиная с 1963 года Общество Фибоначчи издает журнал под названием «Fibonacci Quarterly». Это общество основали математики Вернер Эмиль Хоггатт (1921–1981) и брат Альфред Брюссо (1907–1988) «с целью обмениваться идеями и стимулировать исследования чисел Фибоначчи и смежных тем». С тех пор – вопреки обстоятельствам – «Fibonacci Quarterly» превратился в весьма уважаемый научный журнал по теории чисел. Как с юмором отметил брат Брюссо: «В 1963 году мы собрали теплую компанию – и стали выпускать математический журнал, как и положено компании отпетых зануд». Десятая Международная конференция по числам Фибоначчи и их применению прошла 24–28 июня 2002 года в Университете Северной Аризоны, в городе Флагстафф. И все это – лишь скромная дань уважения человеку, который, при помощи кроликов, открыл математическую концепцию, правящую миром. Однако при всей важности вклада Фибоначчи в развитие науки история золотого сечения в XIII веке не завершилась, и в Европе эпохи Возрождения ее ждали удивительные открытия.