Золотые числа Фибоначчи
Снова рассмотрим последовательность Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 – и на сей раз посмотрим на отношения последовательных членов этого ряда (вычислять будем до шестого знака после запятой):
1/1 = 1,000000
2/1 = 2,000000
3/2 = 1,500000
5/3 = 1,666666
8/5 = 1,6000001
3/8 = 1,625000
21/13 = 1,615385
34/21 = 1,619048
55/34 = 1,617647
89/55 = 1,6180561
44/89 = 1,617978
233/144 = 1,618056
377/233 = 1,618026
610/377 = 1,618037
987/610 = 1,618033
Узнаете это число? Чем дальше мы продвинемся по последовательности Фибоначчи, тем ближе отношение двух соседних чисел Фибоначчи будет колебаться (то чуть больше, то чуть меньше) вокруг золотого сечения, неуклонно приближаясь к нему. Если обозначить n-ный член последовательности Фибоначчи как Fn, а следующий за ним – как Fn+1, то суть нашего открытия состоит в том, что чем больше n, тем ближе отношение Fn/Fn+1 к числу φ. Это свойство чисел Фибоначчи открыл в 1611 году знаменитый немецкий астроном Иоганн Кеплер (а возможно, его опередил неизвестный итальянский математик), однако прошло более ста лет, прежде чем связь между числами Фибоначчи и золотым сечением была доказана, да и то не до конца, шотландским математиком Робертом Симсоном (1687–1768). Кстати, Кеплер, очевидно, открыл последовательность Фибоначчи совершенно самостоятельно, а не из «Книги абака».
Но почему члены последовательности, выведенной из схемы разведения кроликов, подводят нас к соотношению, выведенному из деления отрезка? Чтобы понять эту связь, придется вернуться к поразительной непрерывной дроби, с которой мы познакомились в главе 4. Вспомним, что мы обнаружили, что золотое сечение можно записать в виде:
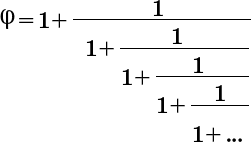
В принципе, можно вычислить значение φ методом последовательных приближений: прерывая непрерывную дробь все ниже и ниже. Предположим, мы именно так и поступим. Тогда у нас получится целый ряд значений (напомню: 1 к a/b – это все равно, что b/a).
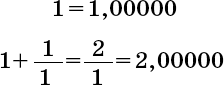
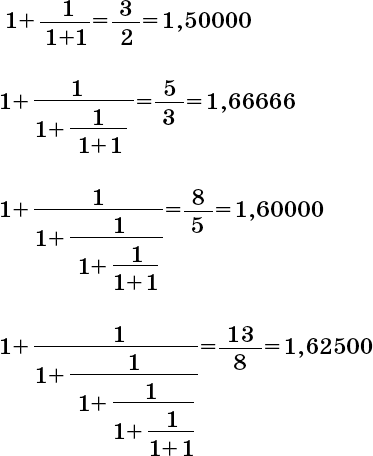
Иными словами, последовательные приближения, при помощи которых мы ищем золотое сечение, в точности равны соотношениям чисел Фибоначчи. Ничего удивительного, что чем дальше мы продвигаемся по последовательности, тем ближе они сходятся к золотому сечению. Это качество прекрасно описано в книге «О росте и форме» знаменитого натуралиста сэра Д’Арси Уэнтворта Томпсона (1860–1948) (Sir D’Arcy Wentworth Thompson. On Growth and Form). Вот как он пишет о числах Фибоначчи: «Один мой друг, сведущий в математике, пишет мне б этих прославленных, поразительных числах: “Вся романтика непрерывных дробей, линейных рекурретнтых последовательностей… все это есть в них, и они – источник бесконечного интереса; как увлекательно наблюдать, с каким рвением они стремятся достичь недостижимого – например, золотого сечения; а ведь это всего лишь одно из сотен подобных соотношений”». Кстати, сходимость золотого сечения объясняет математический фокус, который я показал вам в главе 4. Если определить последовательность чисел так, что каждый член последовательности (начиная с третьего) равен сумме двух предшествующих, то с каких бы двух чисел вы ни начали, если зайти по последовательности достаточно далеко, отношение двух последовательных членов будет приближаться к золотому сечению.
Числа Фибоначчи, подобно «предмету устремлений» их отношений – золотому сечению, – обладают поистине поразительными свойствами. Перечень математических закономерностей, связанных с числами Фибоначчи, буквально бесконечен. Приведу лишь несколько из них.
«Квадрат из прямоугольников»
Если составить сумму нечетного числа произведений последовательных чисел Фибоначчи, например, три произведения 1 × 1 + 1 × 2 + 2 × 3, эта сумма (в нашем случае 1 + 2 + 6 = 9) равна квадрату последнего числа Фибоначчи, которое вы задействовали в произведениях (в нашем случае 32 = 9). Другой пример: возьмем сумму семи произведений 1 × 1 + 1 × 2 + 2 × 3 + 3 × 5 + 5 × 8 + 8 × 13 + 13 × 21 = 441, и эта сумма будет равна квадрату последнего задействованного числа: 441 = 212. Подобным же образом сумма одиннадцати произведений 1 × 1 + 1 × 2 + 2 × 3 + 3 × 5 + 5 × 8 + 8 × 13 + 13 × 21 + 21 × 34 + 34 × 55 + +55 × 89 + 89 × 144 = 1442. Это качество прекрасно видно из чертежа на рис. 30. Любое нечетное число прямоугольников, стороны которых равны последовательным числам Фибоначчи, прекрасно складывается в квадрат. На нашем чертеже таких прямоугольников семь.
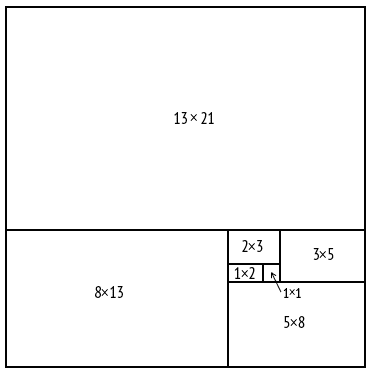
Рис. 30
Греховное число одиннадцать
В драме «Пикколомини» немецкого поэта и драматурга Фридриха Шиллера астролог Сени заявляет: «Одиннадцать – число греховное. Оно зашло за десять – число господних заповедей» («Elf ist die Sünde. Elfe Überschreiten die zehn Gebote») (Пер. Н. Славятинского). Это еще средневековое суеверие. С другой стороны, у чисел Фибоначчи есть свойство, связанное с числом 11, которое отнюдь не грешно, а, наоборот, очень красиво.
Вычислим сумму первых десяти чисел Фибоначчи: 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 = 143. Эта сумма нацело делится на 11 (143/11 = 13). То же самое верно для суммы любых десяти последовательных чисел Фибоначчи. Например, 55 + 89 + 144 + 233 + 377 + 610 + 987 + 1597 + 2584 + 4181 = 10 857, а 10 857 нацело делится на 11: 10 857/11 = 987. Внимательно поглядев на эти примеры, можно заметить еще кое-что. Сумма любых десяти последовательных чисел Фибоначчи всегда равна седьмому из этих чисел, умноженному на 11. Можете воспользоваться этим свойством, чтобы поражать зрителей скоростью, с которой вы сложите любые десять последовательных чисел Фибоначчи.

