При изготовлении одной детали сложной формы потребовалось обжать ее жидкостью со всех сторон во вращающемся состоянии. При этом было поставлено важное условие: давление на деталь должно быть связано с числом оборотов. В общем, как в центрифуге, только наоборот. По мнению технологов, таким образом достигались наилучшие свойства поверхности.

Серьезные специалисты от задачи отмахнулись: кто же будет заниматься глупостями, которые явно противоречат законам природы! А Г.Х. Подойницын, хорошо знакомый с «маленькими человечками», пригласил их в соавторы.

— Сейчас вы работаете так (рис. 9.3), — сказал изобретатель.

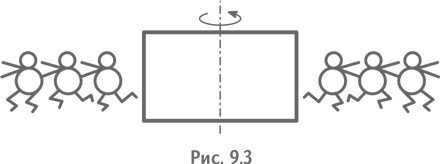
— А я хочу, чтобы вы работали вот так (рис. 9.4).

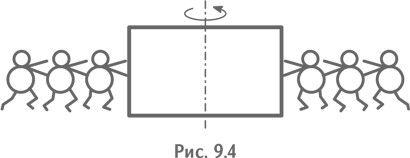
— Чтобы мы так работали, — посмотрев на задание, ответили МЧ, — надо, чтобы кто-то толкал нас к детали, не обращая внимания на то, что мы стремимся от нее уйти. Для этого нужна еще одна группа «человечков». Стенка на стенку (рис. 9.5).

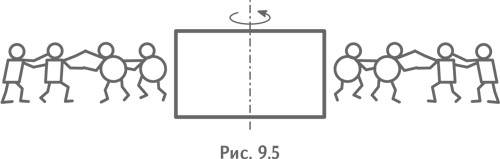
Ведь уйти мы хотим под действием центробежной силы — как только деталь начнет вращаться. И чем быстрее она вращается, тем сильнее нас от нее отбрасывает. Значит, их сила тоже должна расти с увеличением скорости вращения детали, но быстрее, чем наша сила (рис. 9.6).

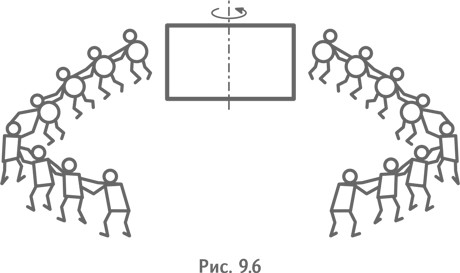
При вращении же больше сила у того, кто тяжелее. Значит, новые «человечки» должны быть тяжелее нас (рис. 9.7).

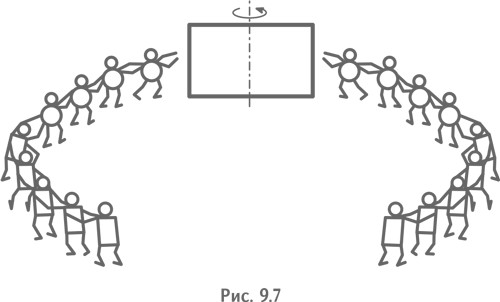
А чтобы мы в драке не смешивались, нас надо сразу разделить!

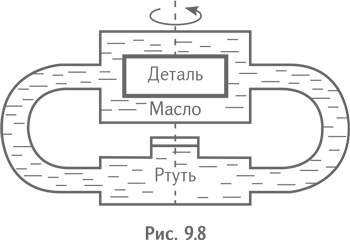
Так появилось решение, противоречащее на первый взгляд всем законам физики. В центрифугу заливают две разные жидкости (масло и ртуть). При вращении центрифуги давление ртути внутрь, на масло, и через него — на деталь оказывается боґльшим, чем давление масла на ртуть, и это давление на деталь пропорционально числу оборотов центрифуги (рис. 9.8).

В 1988 г. один из авторов этой книги (М.И. Меерович) проводил занятия по ТРИЗ с учениками 9–10-х классов средней школы № 36 г. Одессы (сейчас — Ришельевский лицей). Аббревиатуру «ММЧ» ребята однажды расшифровали как «моделирование мыслящими человечками». Чтобы руководить «мыслящими человечками», нужно действительно не бояться смелых идей и обладать сильным воображением. И результаты тогда могут быть самыми неожиданными...

На одном из занятий решали классическую задачу о дозаторе жидкости «Капризная качалка» из книги Г. Альтова (литературный псевдоним Г.С. Альтшуллера) «И тут появился изобретатель...» Приводим описание полностью.