Приложение к главе 4

Чтобы вычислить коэффициент корреляции между двумя совокупностями чисел, вы должны выполнить перечисленные ниже действия, каждое из которых иллюстрируется путем использования данных о значениях роста и веса для 15 гипотетических учащихся в приведенной ниже таблице.

1. Преобразуйте рост каждого учащегося в стандартные единицы: (рост ‒ среднее значение) / стандартное отклонение.
2. Преобразуйте вес каждого из учащихся в стандартные единицы: (вес ‒ среднее значение) / стандартное отклонение.
3. Для каждого учащегося вычислите произведение (вес в стандартных единицах) × (рост в стандартных единицах). Вы должны увидеть, что это число будет самым большим по абсолютному значению, когда рост и вес ученика расположены относительно далеко от своих средних значений.
4. Коэффициент корреляции представляет собой сумму произведений, вычисленных выше, деленную на количество наблюдений (в нашем случае — 15).

Корреляция между ростом и весом для этой группы учащихся — 0,83. Учитывая, что коэффициент корреляции может находиться в диапазоне от –1 до 1, это относительно высокая степень положительной корреляции, чего и следовало ожидать.

A — Учащийся; B — Рост; C — Вес; D — Рост в стан­дарт­ных еди­ни­цах; E — Вес в стан­дарт­ных еди­ни­цах; F — (Вес в стан­дарт­ных еди­ни­цах) × (Рост в стан­дарт­ных еди­ни­цах)

A	B	C	D	E	F
Ник	74	193	1,21	0,99	1,19
Элана	66	133	–0,63	–0,67	0,42
Дайна	68	155	–0,17	–0,06	0,01
Ребекка	69	147	0,06	–0,29	–0,02
Бен	73	175	0,98	0,49	0,48
Чару	70	128	0,29	–0,81	–0,24
Сахар	60	100	–2,00	–1,59	3,18
Мэгги	63	128	–1,32	–0,81	1,07
Фейсал	67	170	–0,40	0,35	–0,14
Тед	70	182	0,29	0,68	0,20
Нарцисо	70	178	0,29	0,57	0,17
Катрина	70	118	0,29	–1,09	–0,32
Си Джей	75	227	1,44	1,93	2,77
София	62	115	–1,54	–1,17	1,81
Уилл	74	211	1,21	1,49	1,80
Среднее значение	68,73	157,33			Итого = 12,39
Стандартное отклонение	4,36	36,12		Коэффициент корреляции = Итого/n = 12,39/15 = 0,83

Формула для вычисления коэффициента корреляции требует небольшого отступления, которое понадобится для того, чтобы объяснить систему обозначений, используемую в данном случае. Символ ∑ часто применяется в статистике. Он обозначает суммирование величин, которые указаны после него. Если, например, имеется некая совокупность наблюдений x₁, x₂, x₃ и x₄, то запись ∑ (x_i) говорит о том, что мы должны суммировать четыре наблюдения: x₁ + x₂ + x₃ + x₄. Таким образом, ∑ (x_i) = x₁ + x₂ + x₃ + x₄. Наша формула для среднего значения совокупности из n наблюдений может быть представлена в следующем виде: среднее значение = ∑ (x_i)/n.

Мы можем придать этой формуле еще более универсальный вид, записав ее как 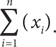 Эта формула означает суммирование величин x₁ + x₂ + x₃ +...+ x_n, или, другими словами, начиная с x₁ (поскольку i = 1) до x_n включительно (поскольку i = n). Наша формула для среднего значения совокупности из n наблюдений может быть представлена в следующем виде:

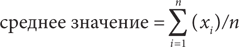
С учетом этой универсальной системы обозначений формула вычисления коэффициента корреляции r для двух переменных x и y может выглядеть так:

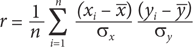
где

n — количество наблюдений;

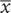_x — среднее значение для переменной x;

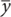_y — среднее значение для переменной y;

σ_x — стандартное отклонение для переменной x;

σ_y — стандартное отклонение для переменной y.

Любая статистическая компьютерная программа может с помощью статистических инструментов вычислить коэффициент корреляции между двумя переменными. Использование Microsoft Excel в примере с ростом и весом учащихся позволяет получить такую же корреляцию между ростом и весом пятнадцати учащихся, что и вычисление, выполненное нами вручную на основе приведенной выше таблицы: 0,83.

Отправить

Рауан

Хорошая книга